峭度滤波器用于电机轴承早期故障特征提取
2014-09-20安国庆秦程郭立炜梁永春
安国庆, 秦程, 郭立炜, 梁永春
(1.河北科技大学电气工程学院,河北石家庄 050018;2.河北科技大学信息科学与工程学院,河北石家庄 050018)
对滤波后的频域信号的为Y1(f)进行傅立叶反变换即可得到滤波后的时域信号y1(t)。
现对y1(t)进行希尔伯特变换
0 引言
轴承故障约占电机故障的40%左右[1]。通常可通过采集轴承时域振动信号,并将其变换至频域,以判断轴承故障是否发生。基于振动信号分析的方法适用于各种类型、各种工况的滚动轴承,是目前应用最广泛的滚动轴承故障诊断方法。
近年来基于振动信号分析的先进算法不断涌现。文献[2]基于能量法对时频谱进行特征提取,利用隐马尔科夫模型对故障特征统计分类,实现对轴承故障的诊断。文献[3]将谐波小波变换、奇异值分解理论和信息熵相结合,从揭示故障信号能量分布的复杂程度入手,提出一种轴承故障实时诊断的新方法。文献[4]提出形态小波包分解与重构算法,能够准确区分不同类型、不同程度的故障序列。文献[5]将构建的各类信号的特征矩阵输入到改进的超球多类支持向量机分类器,判断滚动轴承故障位置及性能退化程度。文献[6]提出一种基于多尺度线调频基的稀疏信号分解方法,并将其应用于非平稳转速下的轴承故障诊断。以上研究对于常规的轴承故障诊断效果显著。但是对于轴承的早期故障,特征信息常常被淹没在背景噪声中不易被识别出来,因此提高信噪比,是电机滚动轴承早期故障诊断的关键。文献[7]采用小波变换实现信噪分离,但小波基和小波参数的选择合适与否将直接影响滤波效果。文献[8]设计了多尺度混合形态滤波器来滤除信号中的噪声及无关的谐波成分,但形态滤波的效果往往与所采用的结构元素有关。文献[9]提出基于ALE的自适应滤波从滚动轴承的振动信号中分离出故障冲击信号,但滤波器的收敛速度和稳定性取决于算法中步长的选择。此外,文献[10]将带通滤波后的振动信号分解成以共振频率为频率成分的正弦基函数的线性组合,文献[11]提出高分辨率谱估计的MUSIC算法提取故障特征,但以上两种方法都需要人为提前确定载波频率的特征带。文献[12]提出先利用AR模型剔除可线性预测的平稳成分,然后利用谱峭度分析凸显故障特征,优势明显。但确定AR模型最优阶次的限定范围仍需人为提前预估。而这些参数的选择取决于操作者的经验或历史数据,经过反复的试验才能确定,给实际应用带来了很多不便。
针对以上问题,提出一种峭度滤波器,使其参数不受人为因素的影响而仅取决于故障信号本身,用于提取在强噪声环境下的电机轴承早期故障信息。首先利用被测振动信号的谱峭度构建一个受控于故障特征信噪比的滤波器,然后对滤波后的信号进行包络分析得到轴承故障谱可凸显故障特征。
1 滚动轴承的故障信号特征
滚动轴承故障按振动信号的特征不同,可以分为两大类:磨损类故障和表面损伤类故障[13]。其中以表面疲劳损伤的危害程度较大,包括点蚀、剥落、裂纹等。当轴承元件表面发生局部损伤时,在滚动体和内、外环相互运动过程中,会与轴承系统的固有振动频率引起谐振,从而产生冲击振动。由于滚动轴承的匀速回转,使冲击具有周期性,对发生在不同位置的损伤,冲击具有不同的频率,通常称为特征频率。轴承外圈故障的计算公式为[14]

内圈故障计算公式为
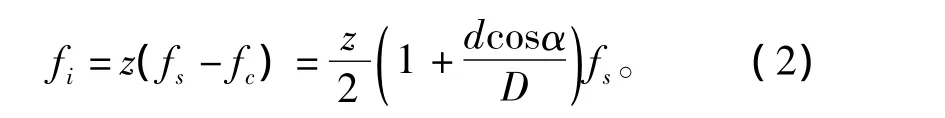
滚动体故障计算公式为
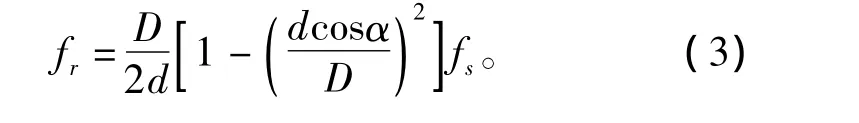
式中:d为滚动体直径;D为轴承节圆直径;α为接触角;z为滚动体个数;fs为旋转频率;fc为外圈的旋转频率。
故障特征频率会出现在振动信号频谱图的相应位置,其幅值可反映该元件的故障程度[15]。
2 构建峭度滤波器提取故障高频调制信息
传统的共振解调方法是频率分析法中最成功的一种,其基本原理是将低频的冲击信号调制到高频的共振频率而远离能量巨大的低频信号[16]。当带有局部缺陷的轴承转动时每转过缺陷处都将会产生冲击,如果轴承按照固定的旋转频率旋转,那么这个冲击将会以固定的频率出现。对共振响应的波形进行解调和傅里叶分析,就可以找到故障频率成分。但是如何合理地选择包络分析的中心频率及其带宽往往制约着工程人员利用共振解调方法可靠诊断轴承的故障。
峭度是反映信号分布特性的数值统计量,是归一化的四阶中心矩。对于一组给定的轴承故障离散振动信号数据,峭度可表示故障形成的大幅值脉冲出现的概率,对时域信号变换的陡峭程度非常敏感,在轴承故障诊断中具有实际意义。由于峭度指标是无量纲参数,与轴承转速、尺寸、载荷等无关,且对冲击信号特别敏感,因此特别适用于表面损伤类故障(尤其是早期故障)的诊断。
现定义故障轴承的实测振动信号为y(t),由被检测的故障信号x(t)和噪声信号n(t)组成,则y(t)可记为
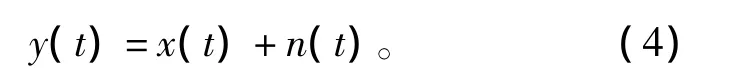
构建一个灵活可变的时频窗w(t),令该窗能够体现频率信息。得到时频函数为

定义一个由窗函数所得的变量

文献[17]经推导指出谱峭度可近似表示为


由式(7)可知,噪信比越小,其对应信号部分的有用信号越强,此时KY(f)越大。因此可利用峭度值的分布情况构建一个与噪信比相关的滤波器,局部地将峭度值应用于不同的频带去细查整个频域,锁定故障信号体现最突出的频带。
现说明谱峭度的计算方法。利用y(t)的短时傅立叶变换结果求出谱瞬时矩。
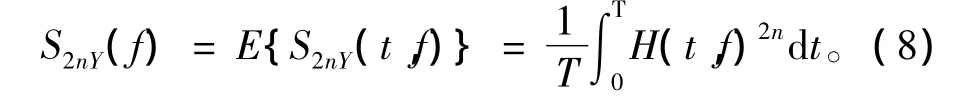
其中T表示短时傅里叶变换结果的时间长度。令n=1和2可分别求出谱瞬时矩S2Y(f)、S4Y(f)。
定义四阶谱累计量为

文献[18]给出谱峭度的计算公式为

构建一个受控于信噪比的滤波器为

根据式(7)和式(11)的共同中间项ρ(f)即可导出滤波器与峭度之间的关系为

由于式(12)中应满足的条件为
现对原信号y(t)进行傅里叶变换得Y(f),对变换后的信号进行滤波,即
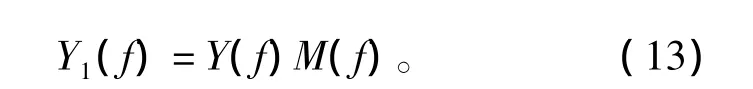
对滤波后的频域信号的为Y1(f)进行傅立叶反变换即可得到滤波后的时域信号y1(t)。
现对y1(t)进行希尔伯特变换

将y1(t)和它的希尔伯特变换y1)构成一个解析信号

幅值A(t)便是给定信号y1(t)的包络,即
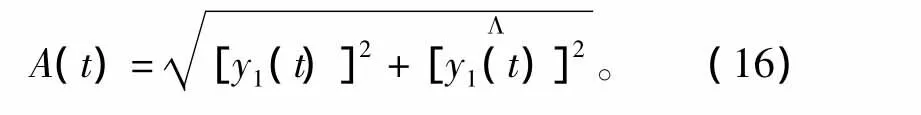
求出其包络分析谱,并对包络分析谱进行傅立叶变换分析,即可得到其故障特征[19]。算法流程如图1所示。

图1 轴承故障诊断流程图Fig.1 Flow chart ofbearing fault diagnosis
3 实验结果及其分析
对型号为Y90S-4的三相异步电机进行了轴承早期故障诊断实验。电机轴承型号为6205-2RS,外径为52 mm,内径为25 mm,厚度为为15 mm,滚珠数目n=13,接触角为0,转速为1 910 r/min,即旋转频率为31.83 Hz。以外圈故障为例,利用电火花在输出轴承的外圈沟道设置直径大约0.8 mm的点蚀,使用USB采集卡和加速度传感器对信号进行采集,采样频率为12 kHz。根据式(1),计算出轴承外圈的故障特征分量为107.4 Hz。
为方便效果比对,实验中对采集的振动信号分别做出了3种处理方式:直接对振动信号进行频谱分析、传统包络分析以及峭度滤波器处理后的包络分析。
轴承外圈故障实测振动信号波形如图2所示。
图2中的噪声信号和冲击信号混合在一起,不能明显地看出冲击成分。

图2 轴承外圈故障振动信号时域波形图Fig.2 Waveform of vibration signal with outer race fault
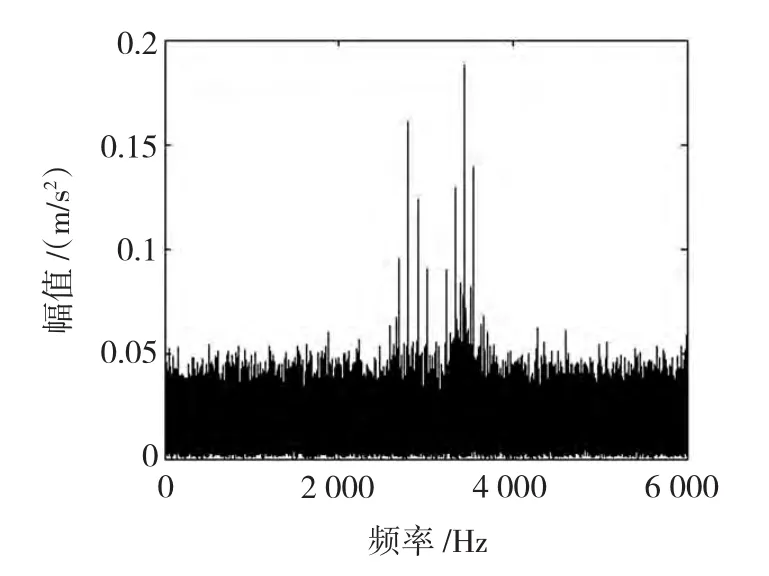
图3 轴承外圈早期故障振动信号的频谱图Fig.3 Spectrum of the vibration signal with incipient outer race fault
从图3中只能在3 000 Hz附近,分辨出轴承故障特征受系统高频固有振动调制形成的较为混乱高幅频段,无法区分出故障类型。而且轴承损伤的低频特征也被淹没于强噪声背景中,难以分辨。
对原信号进行传统包络分析后的频谱如图4所示。

图4 原始振动信号的传统包络分析结果Fig.4 Traditional envelope spectrum analysis
由图4可以看出,故障特征频率107.6 Hz虽能解调出来,但由于处于故障早期,程度较轻微,轴承外圈故障信号的调制特征没有凸显,解调效果欠佳。这主要是因为在进行传统包络谱分析时,解调频带的选取取决于经验,而一般在进行包络谱分析时,选取要解调频带的宽度应该不小于最后的包络谱的宽度,且包络谱至少要包含3倍的最大可能的轴承故障频率,传统包络谱分析不能有效地进行共振频带的选取,这在主观上会给分析结果带来很大影响。
现利用提出的峭度滤波器对信号处理之后,再进行包络分析。所求得的峭度滤波器的幅频特性如图5所示。

图5 谱峭度构造的滤波器Fig.5 Filter constructed by spectral kurtosis
图5中幅值越高表示其对应频率段的噪信比越低(即故障信号越强),图中2 000到3 000段的幅值最高,表示故障在此频率段产生高频共振。
用求得的滤波器对原信号进行滤波后的频谱如图6所示。

图6 滤波后信号的频谱图Fig.6 Spectrum of filtered signal
从图6中可明显地看到调制后的故障特征频带被凸显出来,与故障不相关的噪声被大大削弱。
对滤波后信号进行包络分析的频谱如图7所示。
从图7可明显看出在107.6 Hz处凸显出轴承的外圈故障特征,且与式(1)中计算的理论值107.4 Hz基本吻合。其二倍频和三倍频也能在频谱中清晰地显现出来。因此,峭度滤波对于故障振动信号的消噪处理和特征成分提取具有双重功效,适用于轴承早期故障,即信噪比不高的情况。

图7 滤波后包络信号的频谱图Fig.7 Envelope spectrum of filtered signals
由于对弱信号的处理不当可能导致误判断,为验证该方法的正确性,现对轴承无损伤时的情况进行分析。健康轴承滤波后的包络分析的频谱如图8所示。

图8 无故障情况滤波后包络信号的频谱图Fig.8 Envelope spectrum of the filtered signals without fault
实验表明,在轴承无损伤的情况下,利用该方法得到的包络频谱中未能看到相关轴承故障信息。未出现由于对弱信号的处理不当而导致的误判现象。进一步验证了峭度滤波器对轴承早期故障信息具有较强的敏感性,方法可行。
4 结论
设计了受控于信噪比的峭度滤波器,用于提取电机轴承故障的高频调制信息。实验结果表明,将滤波后的信号进行包络分析可凸显电机轴承故障特征。该滤波器可避开振动信号处理过程中人为因素的影响,较传统包络分析方法具备更高的故障识别率,适用于电机轴承早期故障诊断的情况。由于该方法可在没有信号历史信息的情况下自动提取信噪比,因此也适用于其他强噪声背景下的旋转机械在线监测和故障诊断领域。
[1]孙林,杨世元.最小二乘支持向量机构造的函数链接型神经网络在滚动轴承故障诊断中的应用[J].中国电机工程学报,2010,30(8):82-87.
SUN Lin,YANG Shiyuan.Application of functional link artificial neural networks constructed with least squares support vctor machine in fault diagnosis of rolling bearings[J].Proceedings of the CSEE,2010,30(8):82-87.
[2]王国锋,李玉波,秦旭达,等.基于TVAR-HMM的滚动轴承故障诊断[J].天津大学学报,2010,43(2):168-173.
WANG Guofeng,LI Yubo,QIN Xuda,et al.Fault diagnosis of rolling bearing based on TVAR and HMM[J].Journal of Tianjin University,2010,43(2):168-173.
[3]丁建明,林建辉,杨强,等.基于谐波小波奇异熵的轴承故障实时诊断[J].中国机械工程,2010,21(1):55-58.
DING Jianming,LIN Jianhui,YANG Qiang,et al.Real-time diagnosis of bearing faults based on harmonic wavelet singular entropy[J].China Mechanical Engineering,2010,21(1):55-58.
[4]林勇,周晓军,张文斌,等.基于形态小波理论和双谱分析的滚动轴承故障诊断[J].浙江大学学报,2010,44(3):432-439.
LIN Yong,ZHOU Xiaojun,ZHANG Wenbin,et al.Rolling bearing fault diagnosis based on morphological wavelet theory and bi-pectrum analysis[J].Journal of Zhejiang University,2010,44(3):432-439.
[5]康守强,王玉静,杨广学,等.基于经验模态分解和超球多类支持向量机的滚动轴承故障诊断方法[J].中国电机工程学报,2011,31(14):96-102.
KANG Shouqiang,WANG Yujing,YANG Guangxue,et al.Rolling bearing fault diagnosis method using empirical mode decomposition and hypersphere multiclass support vector machine[J].Proceedings of the CSEE,2011,31(14):96-102.
[6]彭富强,于德介,罗洁思,等.基于多尺度线调频基稀疏信号分解的轴承故障诊断[J].机械工程学报,2010,46(7):88-95.
PENG Fuqiang,YU Dejie,LUO Jiesi,et al.Sparse signal decomposition method based on multi-scale chirplet and its application to bearing fault diagnosis[J].Journal of Mechanical Engineering,2010,46(7):88-95.
[7]罗忠辉,薛晓宁,王筱珍,等.小波变换及经验模式分解方法在电机轴承早期故障诊断中的应用[J].中国电机工程学报,2005,25(14):125-129.
LUO Zhonghui,XUE Xiaoning,WANG Xiaozhen,et al.Study on the method of incipient motor bearing fault diagnosis based on wavelet transform and EMD[J].Proceedings of the CSEE,2005,25(14):125-129.
[8]郝如江,卢文秀,褚福磊.形态滤波器用于滚动轴承故障信号的特征提取[J].中国机械工程,2009,20(2):197-201.
HAO Rujiang,LU Wenxiu,CHU Fulei,.Morphological filters in feature extraction for rolling bearing defect signals[J].China Mechanical Engineering,2009,20(2):197-201.
[9]赵勍波,盛炜佳,张国远,等.基于ALE的自适应滤波在轴承故障诊断中的应用[J].轴承,2009(2):197-201.
ZHAO Qingbo,SHENG Weijia,ZHANG Guoyuan,et al.Application of adaptive filtering in rolling bearing fault diagnosis based on ALE[J].Bearing,2009(2):197-201.
[10]SHEEN Yuhtay.An analysis method for the vibration signal with amplitude modulation in a bearing system[J].Journal of Sound and Vibration,2007,303(3-5):538-552.
[11]夏立,费奇.基于MUSIC算法的感应电机轴承故障检测方法研究[J].电机与控制学报,2005,9(4):392-396.
XIA Li,FEI Qi.A fault detection method of bearing in induction motor based on MUSIC algorithm[J].Electric Machines And Control,2005,9(4):392-396.
[12]石林锁,沈金伟,张亚洲,等.基于AR模型和谱峭度法的滚动轴承故障诊断[J].振动与冲击,2011,30(12):257-260.
SHI Linsuo,SHEN Jinwei,ZHANG Yazhou,et al.Fault diagnosis of a rolling element bearing based on AR model and spectral kurtosis[J].Journal Of Vibration and Shock,2011,30(12):257-260.
[13]席玉洁,马波,冯坤.滚动轴承故障监测诊断中的自适应滤波算法[J].轴承,2011(5):47-50.
XI Yujie,MA Bo,FENG Kun.Adaptive filtering algorithm in fault diagnosis of rolling bearings[J].Bearing,2011(5):47-50.
[14]钟秉林,黄仁.机械故障诊断学[M].北京:机械工业出版社,2006:298-313.
[15]任凌志,于德介,彭富强.基于多尺度线调频基稀疏信号分解的广义解调方法及其在滚动轴承故障诊断中的应用[J].中国电机工程学报,2010,30(11):102-108.REN Lingzhi,YU Dejie,PENG Fuqiang.Generalized demodulation method based on multi-scale chirplet and sparse signal decomposition and its application to roller bearing fault diagnosis[J].Proceedings of the CSEE,2010,30(11):102-108.
[16]刘金朝,丁夏完,王成国.自适应共振解调法及其在滚动轴承故障诊断中的应用[J].振动与冲击,2007,26(1):38-41.
LIU Jinzhao,DING Xiawan,WANG Chengguo.Adaptive resonance demodulation method and its application to fault diagnosis of freight car rolling bearings[J].Journal of Vibration and Shock,2007,26(1):38-41.
[17]蔡艳平,李艾华,石林锁,等.基于EMD与谱峭度的滚动轴承故障检测改进包络谱分析[J].振动与冲击.2011,30(2):168-172.
CAI Yanping,LI Aihua,SHI Linsuo,et al.Roller bearing fault detection using improved envelope spectrum analysis based on EMD and spectrum kurtosis[J].Journal of Vibration and Shock,2011,30(2):168-172.
[18]王晓冬,何正嘉,訾艳阳.滚动轴承故障诊断的多小波谱峭度方法[J].西安交通大学学报,2010,44(3):77-81.
WANG Xiaodong,HE Zhengjia,ZI Yanyang.Spectral kurtosis of multiwavelet for fault diagnosis of rolling bearing[J].Journal Of Xi An Jiao Tong University.2010,44(3):77-81.
[19]DENG Yongjun,WANG Wei,QIAN Chengchun,et al.Boundary processing technique in EMD method and hilbert transform[J].Chinese Science Bulletin,2001,46(11):954-960.
