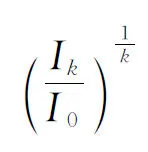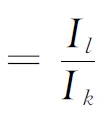关于弦幂积分的一个不等式

张晗方

(江苏师范大学教师教育学院，徐州221116)

设m为非负整数,K为n维欧氏空间En中的有界凸体,G为与K相交的直线，则相交弦长为σ的弦幂积分是[1,2]

(1)

(2)

当且仅当f1(x)∶f2(x)∶…∶fm(x)=const时等号成立.

这是著名的Hölder不等式.

(3)

证由Hölder不等式(2)知

此即不等式(2).

推论1在定理1的条件下，若记p1,p2,…,pm的算术平均为p0，则有

Ip1Ip2…Ipm≥

(4)

推论2[2]在定理1的条件下，对于三个非负整数p1,p2,p3，若0≤p3≤p2≤p1，则有

(5)

将此不等式整理一下便得不等式(5).

定理2设k,l均为正整数，且1≤k

(6)

证在(4)中取m=2,p1=k-1,p2=k+1,则有

(7)

在(7)的两端同取k次幂，则有

(8)

在(8)中分别取k为1,2,3,…,k，则有

将这k个不等式相乘便可得

也即

(9)

由此可得

(10)

由递推不等式(10)立即可得(5).

在文[1,2]中，定义了凸集K的平均弦长为. 实际上，这里的E(σ)是E2中与凸集K的2维与1维体积(即K的面积与周长)相关的弦幂积分I1与I0的比，而在n维欧氏空间En中，我们给出如下的

定义设K为n维欧氏空间中的有界闭凸体，则K的弦长σ的n,m次平均为

(11)

由(11)知，此处显然有E(σ,1,0)=E(σ).

推论3设K为n维欧氏空间中的有界闭凸体，则对于K的弦长σ的l,k(1≤k

E(σ,l,k)≥El-k(σ,1,0)=(E(σ))l-k(1≤k

(12)

实际上，由定理2中的(6)可知

又因为

所以有

[参 考 文 献]

[1] 任德麟. 积分几何学引论[M].上海: 上海科学技术出版社,1988.

[2] Luis Santaló. Integral geometry and geometric probability[M]. Cambridge: Cambridge University Press，2004.