电磁轨道炮固体电枢的运动特性分析*

靳 智，沈培辉，刘 凯

（南京理工大学智能弹药技术国防重点学科实验室，南京 210094）

0 引言

电磁轨道炮因具备弹丸速度高、威力大、发射方便等优点，因此目前各国对它的研究正方兴未艾。电枢作为发射系统的运动组件，国内外专家学者对其进行了不同方面的研究［1］。文献［2］分析了发射状态下导轨的动态响应;文献［3］通过数值模拟分析了二维块状电枢的速度趋肤效应;文献［4］研究了固体电枢非稳态电磁场和温度场;文献［5］研究了电枢导轨接触区几何结构对电枢发射的影响。然而目前现有文献资料对固体电枢的运动特性的研究略显不足，文中将从动力学角度分析固体电枢在激励电流作用下的加速度和速度理论，并运用数值分析软件和有限元分析软件对比分析理论和仿真的区别。此外，讨论了电枢内侧曲率对发射效能的影响。

1 理论分析

电磁发射的基本理论是电流和磁场之间的交互作用，载流体电枢受洛伦兹力作用，从而达到弹丸加速的目的。电磁炮发射需要高能量的脉冲电源，例如单极发电机、磁通压缩器、电容器组等。目前常用的为电容器组，理论上激励电流越平稳越有利于发射，实际上电容器组无法提供恒定的电流。为方便分析，电流参考文献［6］中使用的简化脉冲电流（图1），第一阶段为上升阶段，第二阶段恒定加载，第三阶段为下降阶段，式（1）为电流表达式。

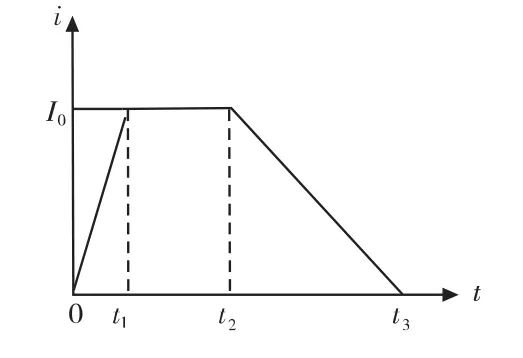
图1 激励电流

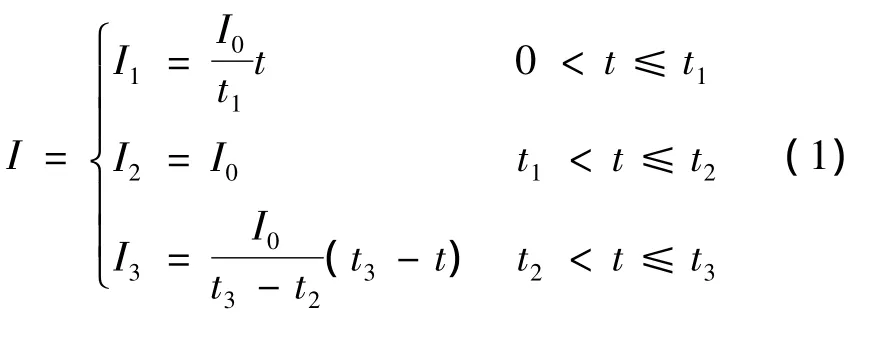
分析电流波形可知，在峰值不变的情况下，通过控制电流放电时间，可以实现不同的电流输出效果。

1.1 加速度分析

峰值电流为I0，根据F=ma=L'I2/2，其中L'为电感梯度，是与长度相关的量，实际过程中电感梯度随电枢运动发生变化，此处仅考虑电流随时间变化，故电感梯度以常量计，I为电枢的电流，m为电枢质量。推导知各阶段的加速度表达式如式（2）所示:

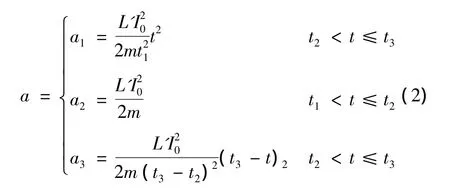
1.2 速度分析

根据分析得到的加速度公式，分别对三个阶段进行如下积分:

式中:V0为电枢初始速度，因从静止开始，故此处为0，进而可以推出速度公式。

1.3 加速长度

导轨加速长度即为电磁力作用下电枢加速运动的距离，即为速度积分结果。

为验证上述理论的可行性，通过有限元模拟与数值模拟对比的方法，分别进行仿真计算，并对计算结果对比分析。

2 有限元模型

为能够清晰直观看到电枢和导轨的有限元模型，因此图2中未给出空气域的有限元模型。使用无穷远单元作为磁场的边界条件，电流输入与输出端与空气边界平行以保证电流的连续性条件。

图2 电枢和导轨有限元模型

3 仿真结果

仿真中使用的峰值电流为I=3 000 kA，脉冲电流各阶段时间分别为 t1=0.5 ms，t2=2 ms，t3=4.5 ms，铝块电枢的质量为24 g，电枢初始速度为0，位于导轨入口，仿真中做了如下假设:

1）数值计算中:导轨电感梯度为0.46μH/m，未考虑摩擦造成的能量损耗，忽略因电枢运动导致的电阻变化。

2）有限元仿真中:轨道、电枢材料分别为黄铜和7075铝合金，为方便对比出口速度，导轨长度尺寸使用理论计算所得尺寸。电枢与导轨之间为面面接触，不计变形，导轨位置固定。

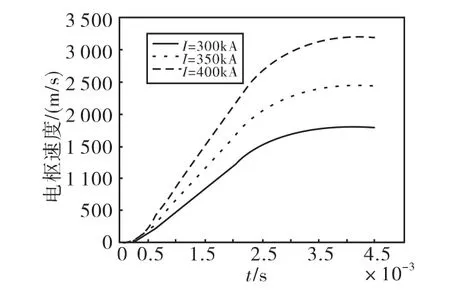
图3 电枢速度随峰值电流的变化

为分析电流对运动速度的影响，故图3中峰值电流分别取了300 kA、350 kA、400 kA，计算得对应的出口速度分别为 1 800 m/s，2 450 m/s，3 200 m/s，能够看出速度随电流增加而增加。结果表明电流大则能量充分，电枢受到的洛伦兹力越大。虽然加大电流可以有效改变电枢的速度，但单位体积的电流密度及焦耳温升也随之升高，这意味着对导轨与电枢的材料性能要求也更高，才能保证连续发射的可靠性。

图4讨论了电枢速度随脉冲电流上升到峰值时间的变化，图中电流上升时间分别为1.5 ms、1 ms、0.5 ms，峰值电流采用300 kA，峰值电流的结束时间点与下降时间点均保持不变，仿真得出口速度分别为1 320 m/s、1 560 m/s、1 800 m/s。结果显示通过缩短激励电流的上升时间，可以显著提高电枢发射速度。与单纯增加峰值电流相比，可节约能源，但这种方法需要有效的控制系统，方可实现增速效果。

图4 电枢速度随电流上升时间的变化

图5 理论和有限元仿真的加速度曲线

图5中分别为理论计算和有限元仿真所得，首先对比加速度曲线与脉冲电流曲线，发现在电流上升阶段（0～0.5 ms），电枢加速度也呈上升趋势，此阶段随着流经电枢的电流持续增加，导轨之间产生的磁感强度增强，则作用于电枢的洛伦兹力也随之增加。持平阶段（0.5～2 ms），电流恒定，故加速度曲线无明显变化。下降阶段（2～4.5 ms），电流逐渐降低直至放电结束，磁场与电流均变弱，因而电枢加速趋势变缓。其次，虽然理论与有限元仿真的加速度曲线近似一致，但在同一时刻理论结果大于仿真数值。对应最大值分别为720 000 m/s2、666 521 m/s2。这种偏差原因在于理论仿真计算中仅考虑了电流随时间的变化，而有限元计算中影响因子除电流外，还包括电场与磁场之间的相互耦合造成的电枢受力变化以及运动引起的阻值变化，电枢与导轨之间的摩擦损耗等，这些因素的综合作用致使电枢受力要小于理论仿真的结果。

图6为理论及有限元仿真的速度曲线。分析得出电枢速度随时间的增加而上升，最终趋于平缓。类似于加速度曲线的误差，同样有限元仿真低于理论仿真的结果，理论与有限元仿真得到的炮口出速分别为1 800 m/s、1 690.42 m/s。以上分析表明上述基本理论虽然在一定程度上与实际情况存在误差，但用来分析电枢的运动特性是可行的。

4 计算分析

为了减少实际发射中电枢的损耗，提高发射效率，缩短理论与实际的误差，为此从结构改进方面入手，以期达到提高出口速度的效果。文献［5］中分析了电枢的臂端长度对电枢发射的影响，故文中重点着手于分析内侧槽部曲率半径对发射的影响。如图7所示，设计了四种不同曲率的电枢，由于电流具有趋肤效应，电枢头部对电磁影响较小，在不同半径下，对头部质量进行控制，以保证电枢在质量上相等。

图6 理论和有限元仿真的速度曲线

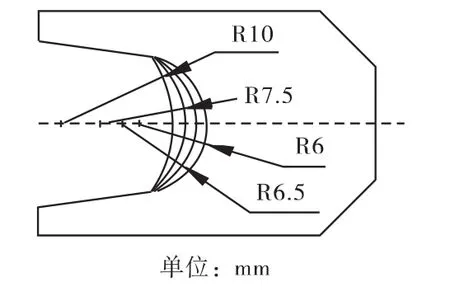
图7 不同曲率半径的二维电枢模型

表1四种结构出口速度对比

表1给出了四种不同曲率半径的电枢运动参数。据表可知结构质量存在偏差，计算得到其最大误差仅为0.43%，对于整体的分析产生的影响可忽略。分析表明随着曲率半径的减小，电枢的出口速度随之增大。与理论速度（1 800 m/s）的差距从6.08% 缩小至4.15%，炮口动能得到了改善。曲率半径变小，电流从臂端到头部平缓过渡，避免因电枢拐角处的曲率过小导致的电流密度过分集中及方向突变，同时改善了电流的趋肤效应，则磁场与电场的作用较平稳，电枢上的洛伦兹力矢量和增加。但内槽曲率半径不能无限小，在质量不变的前提下，曲率半径小意味着臂端的伸长或头部质量的增加，从保持电枢与导轨的接触压力及增加有效推力来看，增加臂端长度后效果并不佳。其次，电枢在运动过程中臂端过长易产生变形、电弧烧伤、磨削等不稳定情况。头部过重易引起电枢运动不稳定。因此，合理的电枢内侧曲率有利于改善轨道炮的发射效能。

表2 四种结构不同时刻的加速度

为进一步分析电枢槽内曲率半径对电枢受力的影响，表2给出了电枢不同时刻的加速度值。从表中数据可知，同一时间点电枢曲率半径减小，加速度的数值却呈上升趋势，以2.5 ms时刻为例，同比R10，加速度分别提高了 1.3%、2.1%、2.4%。文中分析未考虑电流焦耳热及电枢与导轨摩擦生热产生的温升，会产生一定的误差。

5 结论

1）通过分段积分得到了电枢的运动方程，在激励时间不变情况下，增加峰值电流可以提高电枢的出口速度，同时需要合适的电枢材料以满足高速发射，防止高温、高应力等造成的烧蚀、刨削等现象;其次，控制加载时间也可以达到不同的发射状态，因而电磁发射不仅需要高能电源，且需要复杂的控制电路系统提供支持。

2）数值模拟和有限元仿真结果表明，两种方法虽存在偏差，但最终得到的规律具有一致性。

3）合理改善电枢的结构可以提高电枢的发射效能，通过对比分析了 R10、R7.5、R6.5、R6 四种结构对电枢运动特性的影响，结果表明随着曲率半径的减小，电枢的出口速度增加，曲率半径为R6时发射效果较好。

［1］贺翔，曹群生.电磁发射技术研究进展和关键技术［J］.中国电子科学研究院学报，2011，6（2）:130－135.

［2］杨玉东，王建新，薛文.轨道炮速度趋肤效应的分析与仿真［J］.强激光与粒子束，2011，23（7）:1965 －1968.

［3］田振国，白象忠，杨阳.电磁轨道炮发射状态下导轨的动态响应［J］.振动与冲击，2012，31（2）:10－13.

［4］李昕，翁春生.固体电枢非稳态电磁场和温度场的数值计算［J］.火炮发射与控制学报，2008，4（3）:48 －51.

［5］刘志明，孙江生，王莹.轨道炮固体电枢的设计［J］.华北工学院测试技术学报，2000，14（3）:158－161.

［6］Laura Rip，Sikhanda Satapathy，Kuo-Ta Hsieh.Effect of geometry change on the current density distribution in C-shaped armatures［J］.IEEE Transactions on Magnetics，2003，39（1）:72 －75.