变异函数模型参数估计的信息熵加权回归法*

潘家宝 戴吾蛟 章浙涛 黄大伟

1)中南大学测绘与国土信息工程系，长沙 410083

2)湖南省精密工程测量与形变灾害监测重点实验室，长沙 410083

变异函数模型参数估计的信息熵加权回归法*

潘家宝1，2)戴吾蛟1，2)章浙涛1，2)黄大伟1，2)

1)中南大学测绘与国土信息工程系，长沙 410083

2)湖南省精密工程测量与形变灾害监测重点实验室，长沙 410083

将熵权理论引入到变异函数理论模型的参数估计中，对加权多项式回归的加权方法进行改进，以信息熵定权，并用实际变形监测数据进行实验。实验结果表明，该方法综合了距离和样本点对数对权重的影响，加权回归确定的变异函数模型更准确，插值预报效果更优。

信息熵;变异函数;加权回归;变形监测;交叉验证

克里金插值在地学领域已经得到了广泛的应用，其中变异函数模型参数的估计是克里金插值的关键。最初使用的方法是人工拟合法，但是该方法耗时费力，效率低，而且主观性强，缺乏统一客观的标准［1－2］。最小二乘法则无法反映变异函数曲线中前几个点的重要性，但前几个点距离较小，它们在反映变量的空间相关性方面极为重要，其可靠性比后面点的可靠性强得多。许多学者提出了一些相应的处理方法［2－4］。在钻探领域，钻孔一般是等间距或近似等间距的，步长较小时样本点对数就多，权重就大，反之则样本点对数就少，权重就小。而在变形监测领域，监测点之间的距离各不相等，样本点的对数无法反映出变异函数曲线前面几个点的重要性，此时以样本点的对数为权重则不能很好地反映权重的实际情况。熵权法全面考虑几种因素的共同影响，合理分配各因素的比例，定权更加全面和科学。本文首先对变异函数理论模型进行线性化［5］，随后以信息熵作为衡量权重的因子进行加权回归来估计模型的参数，最终得到基于信息熵的加权回归模型，并以实际变形监测的数据验证了该方法的可靠性。

1 变异函数模型及线性化

常用的变异函数理论模型主要有球状模型、指数模型和高斯模型［1］。球状模型为:

当0＜h＜3a时，对式中exp(－h/a)进行泰勒级数展开，随着泰勒级数阶数的增加，参数的变化将逐渐减小，参数趋于稳定。因此，只需展开到二阶平方项:

同球状模型类似，此时γ(h)可以线性化为γ(h)=b0+b1x1+b2x2。高斯模型为:

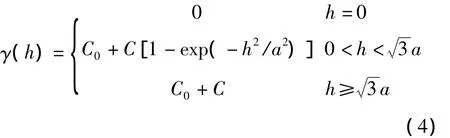
同指数模型线性化过程类似，γ(h)可以线性化为γ(h)=b0+b1x1+b2x2。幂函数模型为:

两边取对数则可以得到:

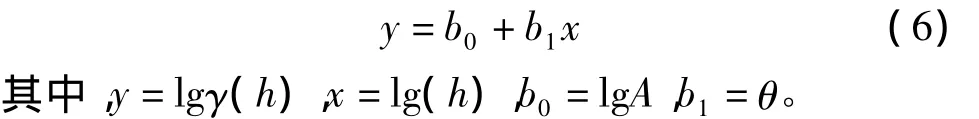
2 利用信息熵加权回归法估计模型参数

2.1 变异函数线性回归方程

对于球状模型、指数模型和高斯模型，令y=γ(h)，得到多元线性回归方程为:

参数求解公式为:

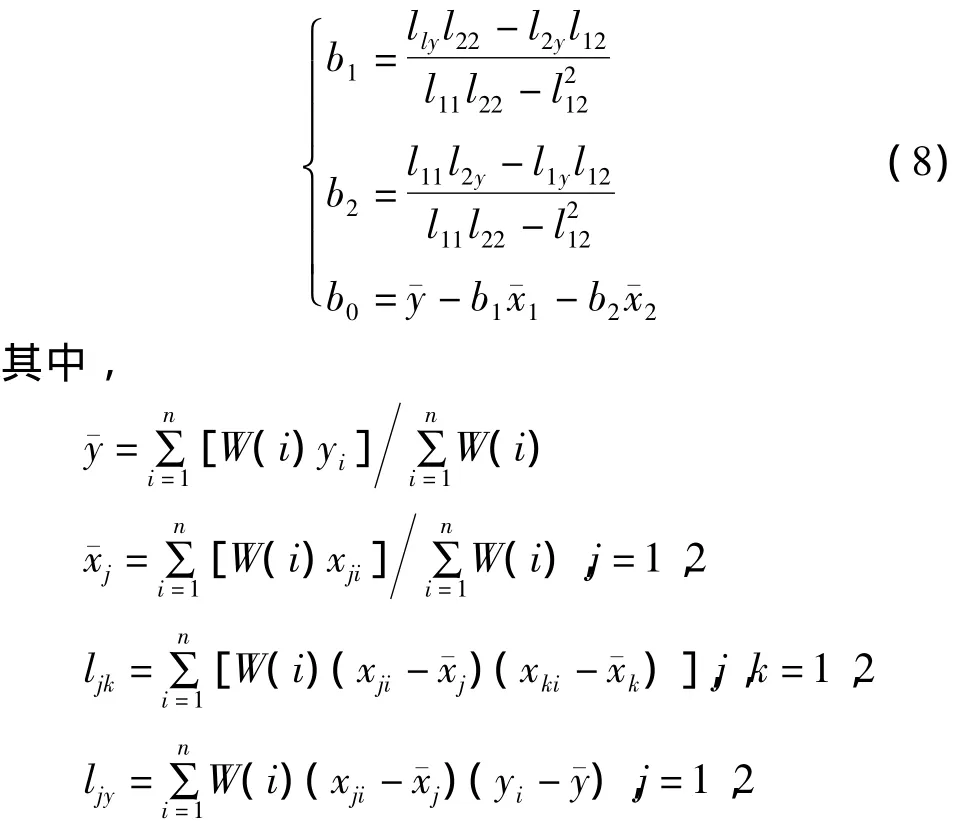
幂函数模型线性化后为一元回归模型，其参数求解公式为:

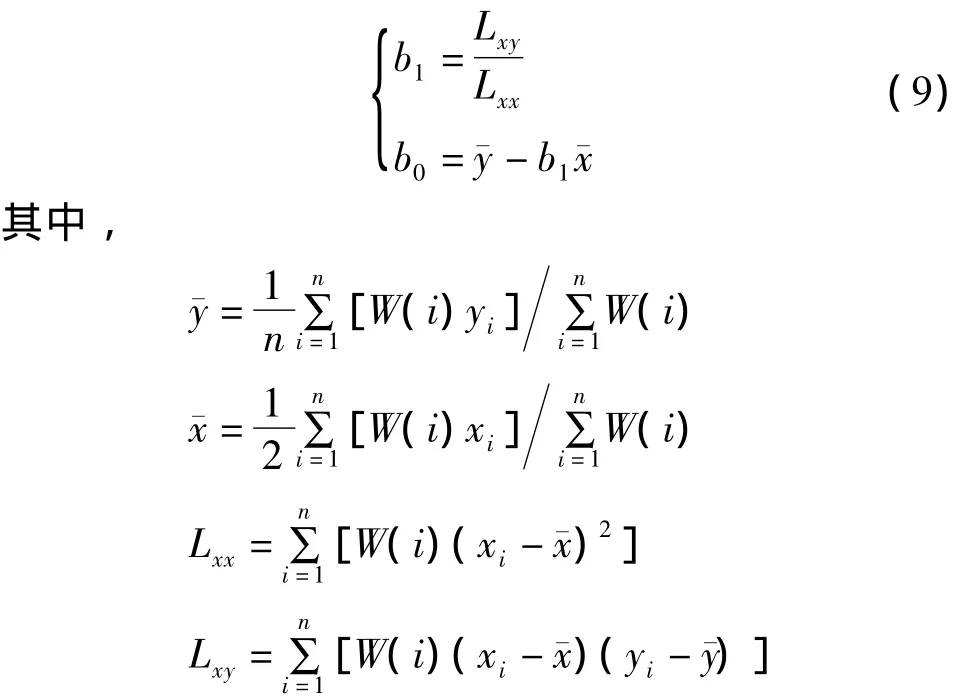
式中W(i)为权重，距离小的样点比距离大的样点在反映变量空间相关性方面更为重要，权重也更大。

2.2 利用熵权法确定变异函数的权重

若系统处于多个不同的状态，而每种状态出现的概率为 pi(i=1，2，…，m)，则其熵定义为［6］:

设有m个待评价项目，n个评价指标构成的评价矩阵 R=(rij)m×n，熵权法定权的步骤如下［7－9］:

1)根据评价矩阵计算每个待评价项目出现的概率:

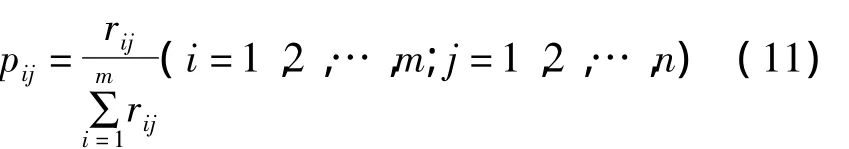
2)计算第j个指标的熵:

3)计算第j个指标的熵权:

4)确定变异函数的最终权重:

3 变形监测数据空间插值

以天津市GPS监测的2006～2007年12个点的沉降量为例，首先根据坐标计算出每两个GPS点之间的距离，然后对距离进行分组［2，10］。若距离落入［kh±ε(h)］(k为常数，ε(h)为容差)范围内就分在同一组，认为这些点间的距离为kh，统计落入［kh±ε(h)］范围内的距离数目，记为N(k)。然后分别求出距离为kh时的实验变异函数值γ(h)，绘制实验变异函数散点图，如图1可以看出，变异函数大致服从幂函数分布，选择幂函数模型进行加权回归估计模型参数。

图1 实验变异函数散点图Fig.1 Scattergram of experimental variogram

分别以距离kh和距离kh的数目N(k)为影响因子构造评价矩阵 R，令 k=1，2，…，n，ε =1/3，最终将距离分成了18组，得到的评价矩阵为:

由式(11)～(14)求得最终的权重Wi如表1。

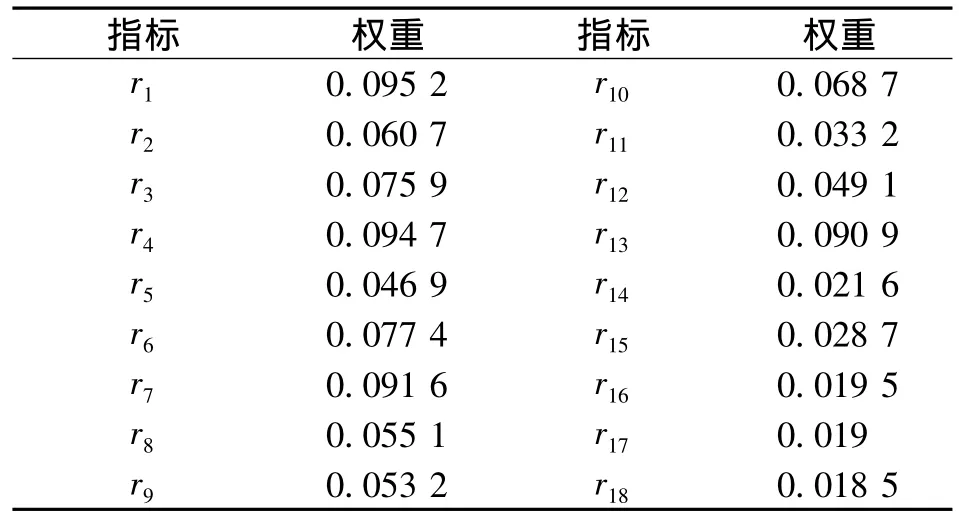
表1 评价指标权重Tab.1 Weights of evaluating indicator

加权回归求得的幂函数模型参数A=0.998 4，θ=2.055 6。当 θ≥2 时，令 θ=1.999 9，变异函数的幂函数模型为:

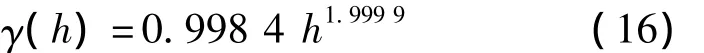
用加权回归得到的幂函数模型进行克里金插值，用交叉验证法检验各点的插值结果(表2)。交叉验证法将观测值中的一个点剔除，用剩余观测点的值估算被剔除点的值，然后再把该点还原，重复以上步骤得到每个观测点上的估计值。然后用统计学的方法将测点上的估计值和实测值两组数据进行统计分析，评价插值方法的精度。

常用的评价指标有［11，12］平均估计误差百分比(PAEE)、相对均方差RMSE、均方根预报误差RMSPE以及残差分析(残差均值RM以及残差标准差RSTD)等。

平均估计误差百分比为:

式中，Z*(Xi)为位置Xi处的克里金插值，Z(Xi)为实测值，¯Z为所有沉降值的平均值，s2为所有沉降值的方差。

由表2可以看出，信息熵加权回归方法建立变异函数模型得到的克里金插值明显优于最小二乘法。其中tja2点使用新方法的预报残差值有异常，与真实值差距较大，比最小二乘的预报结果差，这可能是因为tja2点所在地区的构造运动或含水砂层逐渐恢复引起的［13］，也可能是由于该地区地处丘陵地带，相对封闭且海拔较高，与其他点的空间相关性有所降低造成的。再分别计算两种方法交叉验证的各项指标，由表3可看出，除残差均值外，加权回归的各项指标均明显优于最小二乘方法。

表2 交叉验证表(单位:m)Tab.2 Cross validation table(unit:m)

表3 交叉验证指标统计(单位:m)Tab.3 Statistics of cross validation Indicators(unit:m)

4 结论

对变异函数模型参数估计的加权回归方法进行改进，提出了以信息熵为权重的加权回归法。熵权法减少了人为主观性对评价过程的干扰，更客观地反映了样本数目和距离对变异函数权重的贡献率。在变形监测中的应用表明，使用信息熵来确定变异函数的权重是一种比较可靠的加权方法，建立的变异函数模型更准确，插值结果也比最小二乘法更优。

1 刘爱利，王培法，丁园圆.地统计学概论［M］.北京:科学出版社，2012.(Liu Aili，Wang Peifa，Ding Yuanyuan.Introduction to geostatistics［M］.Beijing:Science Press，2012)

2 王仁铎，胡光道.线性地质统计学［M］.北京:地质出版社，1988.(Wang Renduo，Hu Guangdao.Linear geostatistics［M］.Beijing:Geological Press，1988)

3 矫希国，刘超.变差函数的参数模拟［J］.物探化计算机技术，1996，18(2):157 － 161.(Jiao Xiguo，Liu Chao.Estimation of variation parameter［J］.Computing Techniques for Geophysical and Geochemical Exploration，1996，16(2):157 －161)

4 李冠林，等.改进的克里金法在海面风场计算中的应用［J］.气象水文海洋仪器，2013(1):73 －76.(Li Guanlin，et al.Application of improved Kriging to calculating sea wind field［J］.Meteorological，Hydrological and Marine Instruments，2013(1):73 －76)

5 李玲，等.变异函数线性化的统一参数估计方法研究［J］.长江大学学报:理工卷，2010(2):127 －129.(Li Ling，et al.Study on the unity parameter estimation method of linear variogram［J］.Journal of Yangtze University:Nat Sci Edit，2010(2):127－129)

6 周访滨，朱建军，陈永奇.基于熵的数据污染率估算［J］.大地测量与地球动力学，2013(4):92－95.(Zhou Fangbin，Zhu Jianjun，Chen Yongqi.Contamination rate estimation based on entropy［J］.Journal of Geodesy and Geodynamics，2013(4):92－95)

7 谢赤，钟赞.熵权法在银行经营绩效综合评价中的应用［J］.中国软科学，2002，9(4):60 － 63.(Xie Chi，Zhong Zan.Entropy method and its application in comprehensive evaluation of bank’s performance［J］.China Soft Science，2002，9(4):60 －63)

8 王永弟，许承权.熵权理论在测量平差中的应用［J］.测绘通报，2012(11):52 － 54.(Wang Yongdi，Xu Chengquan.Application of entropy theory to measurement adjustment［J］.Bulletin of Surveying and Mapping，2012(11):52 －54)

9 刘玉成.熵法确定权重的地基沉降组合预测模型［J］.中国科技论文在线，2010，5(11):875 －878.(Liu Yucheng.A combined prediction model for foundation subsidence using the entropy weight method［J］.Sciencepaper Online，2010，5(11):875－878)

10 程勖，等.变异函数在异常空间插值中的应用［J］.世界地质，2007，26(3):298 － 303.(Cheng Xu，et al.Application of variogram in interplation of abnormal space［J］.Global Geology，2007，26(3):298 －303)

11 顾春雷，杨漾，朱志春.几种建立 DEM模型插值方法精度的交叉验证［J］.测绘与空间地理信息，2011，34(5):100 －102.(Gu Chunlei，Yang Yang，Zhu Zhichun.Accuracy cross-validation of several interpolation methods of DEM［J］.Geomatics ＆ Spatial Information Technology，2011，34(5):100－102)

12 张晓明，赵剡.基于克里金插值的局部地磁图的构建［J］.电子测量技术，2009，32(4):122 －125.(Zhang Xiaoming，Zhao Yan.Local geomagnetic field mapping based on Kriging interpolation method［J］.Electronic Measurement Technology，2009，32(4):122 －125)

13 易长荣，王淼，徐冬.GPS连续站监测天津市地面沉降的初步结果［J］.现代测绘，2009(1):12.(Yi Changrong，Wang Miao，Xu Dong.Preliminary results of land subsidence monitored by continuous GPS stations in Tianjin［J］.Modern Surveying and Mapping，2009(1):12)

PARAMETER ESTIMATION OF VARIOGRAM MODEL BY USING INFORMATION ENTROPY WEIGHTED REGRESSION

Pan Jiabao1，2)，Dai Wujiao1，2)，Zhang Zhetao1，2)and Huang Dawei1，2)
1)Department of Survey Engineering and Geomatics，Central South University，Changsha 410083
2)Key Laboratory of Precise Engineering Surveying ＆ Deformation Disaster Monitoring of Hunan Province，Changsha410083

The information entropy theory was introduced into parameter estimation of variogram model，to improve weighting method of weighted polynomial regression using the entropy weight method.An experiment was taken with real deformation monitoring data，considering the influence of both distance and the number of point pairs at the same distance.The experimental results show that the variogram model determined by information entropy weighted regression is more reasonable，and interpolating prediction is more accurate.

information entropy;variogram;weighted regression;deformation monitoring;cross validation

P207

A

1671-5942(2014)03-0125-04

2013-09-24

国家自然科学基金项目(41074004);国家973计划项目(2013CB733303)。

潘家宝，1989年生，男，硕士研究生，主要从事变形监测和时空Kalman滤波方法的研究。E－mail:story_cn@163.com;panjiabao@csu.edu.cn。