顾及不同约束准则的变形并联组合预测模型研究*

高彩云 崔希民 高 宁

1)中国矿业大学(北京)地球科学与测绘工程学院，北京 100083

2)河南城建学院测绘工程学院，平顶山 467044

顾及不同约束准则的变形并联组合预测模型研究*

高彩云1，2)崔希民1)高 宁2)

1)中国矿业大学(北京)地球科学与测绘工程学院，北京 100083

2)河南城建学院测绘工程学院，平顶山 467044

根据权重求取的不同约束准则，对变形并联组合预测模型的构建进行研究。分别构建了非最优、最优权、灰色综合关联度定权、熵权、神经网络非线性5类变形并联组合预测模型，讨论了5类约束准则下的权重求取特点，并比较了预测的效果。分析表明，基于神经网络的非线性组合预测具有良好的特性和较高的预测精度。

变形;并联模式;约束准则;权值;组合预测

各类变形体的变形过程可以看做是一个复杂的非线性动力学系统，很难用单一的数学模型对其形变规律进行准确预测［1－3］。为充分利用各种单项预测模型所提供的有用信息，研究人员对变形的组合预测进行了研究，取得了较好的效果［3－7］。针对变形组合预测模型的构建问题，文献［7］解决了组合模型的构造形式和求解准则的问题，并提出了基于变形信号分解的串联式、基于信息综合利用的并联式两类组合模型。并联式组合模型构建的关键是合理地确定单项预测模型在组合预测中的权重，这就涉及其求解的约束准则。目前，权重的确定方法有很多种，对某一预测问题采取不同的约束准则求解权重，所得结果不尽相同，从而预测结果及精度也不尽相同。文献［7－8］仅对线性定权和非线性定权的预测效果进行了比较，得出非线性定权组合优于线性定权组合的结论。本文将讨论在其他约束准则下权值的求解及其对组合预测的影响。

1 基于并联模式的组合预测模型

并联模式组合，是指针对某一变形预测问题，首先根据监测数据的变化特点，合理地选取多种单项预测模型，然后在某种约束条件下求取单项预测模型在组合预测中的权重，进而以权值为约束条件，组合单项预测结果。其算法流程如图1所示。

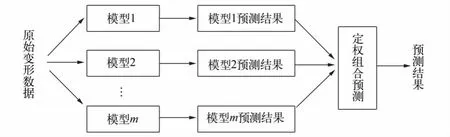
图1 并联预测建模流程图Fig.1 Flow chart of parallel combination prediction model construction

2 顾及不同约束准则的并联组合模型

并联组合预测的关键是单项模型权值的求解。根据权值求取约束准则的不同，可以从不同的视角对其进行分类:1)按组合函数关系，可分为线性组合与非线性组合;2)按权系数计算方法，可分为最优组合和非最优组合;3)按权值系数是否随时间变化，可分不变权组合与变权组合;4)根据单一预测模型包含的信息量的多少，采用熵值定权;5)利用灰色关联度进行定权。

2.1 基于最优约束的并联组合

最优并联组合预测方法的基本思想是根据某种准则的目标函数，在一定的约束条件下求得目标函数的最大值或最小值，从而求得组合预测方法的加权系数。可以表示成如下数学规划问题:

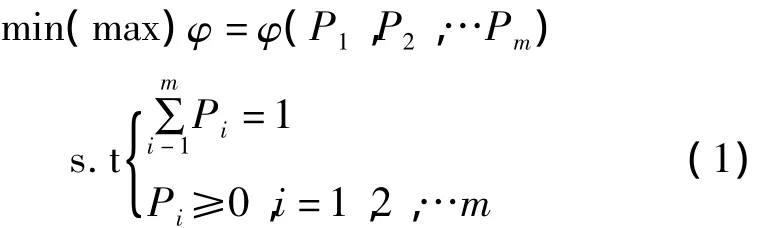
式中，φ为目标函数，Pi为单项预测模型的权值。

2.2 非最优约束下的并联组合

非最优约束下的并联组合模型是依据某个特定指标进行权值的确定，通常可采用算法平均法、预测误差平方和倒数法、简单加权平均法、均方误差倒数法等。下面仅以预测误差平方和倒数法为例构建并联组合模型。

预测误差平方和倒数法的基本思想是根据预测模型误差的平方和来确定权值的大小，预测误差平方和越大，则权值系数较小，表明该项预测模型精度越低;反之，则赋予较大的权值系数:

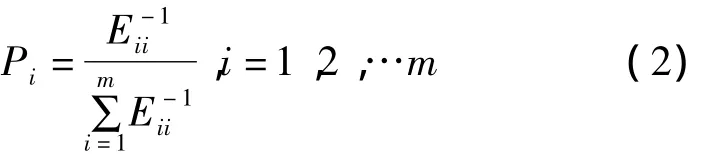
式中，∑Pi=1，Pi≥0，其中 Eii为第 i种单项预测模型的误差平方和。

2.3 灰色综合关联度约束定权

灰色理论将变形系统的演化过程看作是在某个区域变化的灰动力学系统，利用灰色综合关联度可以对变形系统的发展规律进行度量。

设变形监测序列为yi，采用某种单项预测模型预测值为^，则二者的灰色综合关联度为:

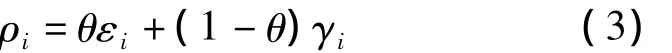
式中，εi为灰色绝对关联度;γi为灰色相对关联度;θ∈(0，1)，通常取0.5，该参数用于调节绝对关联度和相对关联度对于综合关联度的影响程度(εi和γi的详细计算过程见文献［9］)。根据各单项模型的预测结果与实际变形值的综合灰色关联度，确定各单项预测模型的相对权重Pi:

2.4 熵值约束定权

设某动态系统可能处于几种不同状态，每种状态出现的概率为Pi，则系统的熵可定义为:

则各单一预测模型的权重为:

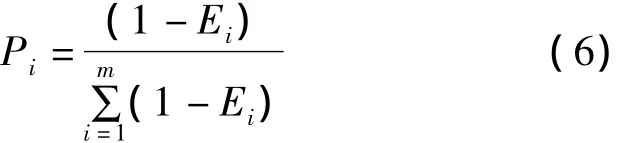
2.5 基于神经网络的非线性约束组合

从定权的过程来看，上述几种约束定权的方法是一种静态定权的过程，权值一旦确定，则在组合预测过程中保持不变。因而，提出基于神经网络的动态定权方法。

针对某变形系统的预测问题，采用m种方法对某变形序列 y={yt}(t=1，2，3，…，n)进行预测，则存在m种预测结果。将预测值(i=1，2，…，m，t=1，2，…，n)作为神经网络的输入，变形观测序列yt作为网络的输出。yt是^yit之间的最优组合，各单项方法在组合预测中的权重可通过神经网络学习训练得到。

3 不同约束准则下的权值特点

不同约束准则存在以下特点:

1)从定权方式看，最优约束和非最优约束两类组合定权的基础是以预测误差为载体建立的，在求解过程中受预测残差影响较大;而灰色综合关联度约束定权从单项预测模型预测值和实际监测值的相关性出发确定权重;熵值约束定权从单一预测模型所提供的信息确定性大小出发，以系统所处状态的概率为基础，进行权值的分配。

2)基于神经网络的非线性定权过程，是按单一样本误差和总体误差满足给定精度要求，由神经网络在自适应动态学习中给出;权值的求取过程随着单项预测误差的改变而变化，权值包含了多重信息，且是一动态的过程。

3)从模型建立过程来看，前4类约束准则的定权方式均是某种数学约束规划问题，权值的分配过程存在假定约束条件;而神经网络定权方法则是自适应的过程，能突出有效信息，发挥各个单项方法的优点，更适应预测环境的变化。

4 算例分析

计算分析以某高层建筑36期沉降变形数据为例，观测数据见文献［10］。

4.1 不同约束准则下权重差异比较

为讨论不同约束准则下，单项预测模型在组合预测中权重的差异性，采用上述变形数据进行建模。选取3种单项预测模型——时序AR(3)、灰色GM(1，1)、RBF神经网络(注:采用二维区间的优化参数 SPREAD=0.16，GOAL=0.013)，利用 1 ～30 期数据进行建模，对31～36期进行组合预测。利用§2中的5种约束准则进行权重的求取。为了便于描述，记:方案1，预测误差平方和最小为约束条件;方案2，预测误差平方和倒数法;方案3，灰色综合关联度定权;方案4，熵值定权;方案5，神经网络的非线性约束定权(注:选取广义回归神经网络GRNN进行建模组合;GRNN的平滑参数经交叉验证搜索优选为0.122)。

5 种约束准则下，3种单项预测模型的权值如表1所示。

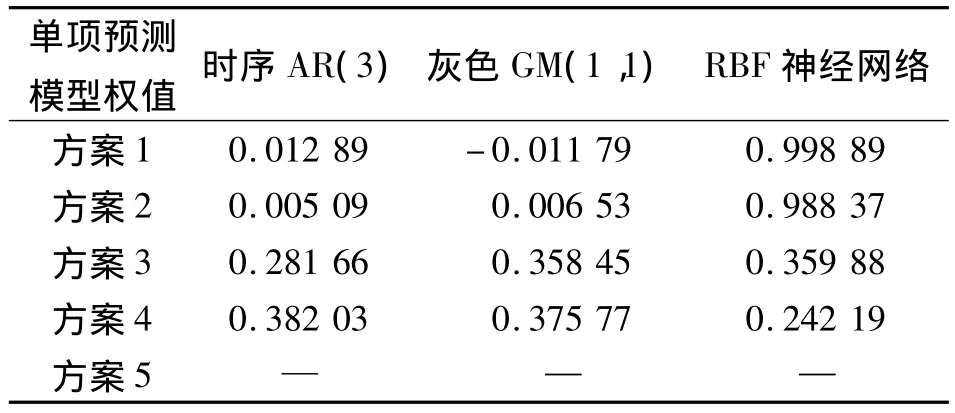
表1 不同约束准则下单项预测模型权值Tab.1 The weights of single prediction model under different restriction criterion

由表1可知，不同约束准则下，3种单项预测模型所占权值差异性较大。比较方案1和方案2的权值发现，权值的求取和单项预测模型的残差(因篇幅限制略去)存在很大的依赖关系，且方案1中以误差平方和最小为目标函数解算最优组合预测的权系数为负值，这在形变预测界存在一定的争议，该值并无实际意义。从权重确定的原则而言，该方法所能提供的信息量被其余方法覆盖，所以在实际计算中该方法权重应为0。在这两种方案中，RBF的模拟效果较好，故所占权值比重很大。方案3与方案4中，权值的分配相对均匀，但其定义权的角度有别于方案1和2。方案3是用灰色综合关联度来挖掘各模型预测值的发展曲线与变形监测历史值的相似程度，方案4则是从熵值的角度重新定义预测误差序列的变异程度，并给出计算组合预测的加权系数。

4.2 不同约束准则组合预测效果比较

由于方案5权值确定的动态性，并未体现出方案5的特性，故从预测的角度比较方案5与其他方案的差异。预测效果如表2所示，以均方误差作为衡量标准。对预测效果进行评价，如表3所示。

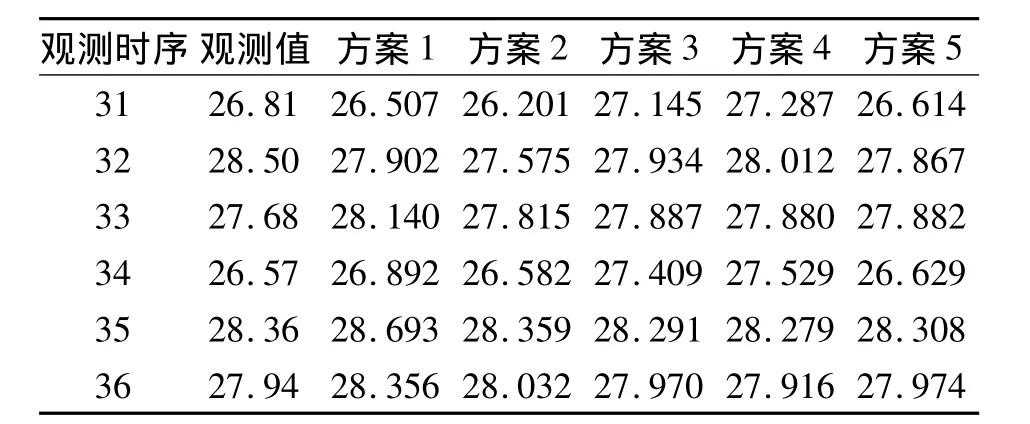
表2 不同约束准则下预测效果比较(单位:mm)Tab.2 The prediction effect under different restriction criterion

表3 5种约束准则下预测精度比较Tab.3 Performance evaluations of each five model

由表2、表3可知，不同约束准则下所构建的并联组合模型在预测效果方面存有较大差异，基于神经网络的非线性并联组合预测效果最优(方案5)，方案1次之，方案4预测效果最差。主要原因如下:方案5的构建过程是一动态过程，其权值在不同的观测时刻能根据单一模型误差适时调整，更适合形变预测;方案1在定权过程中出现了负权(表1)，在组合过程中将负权的单项预测模型略去(略去灰色GM(1，1))，仅组合了预测效果较好的AR和RBF神经网络，故也取得了较好的预测效果;方案3根据单项预测和实际观测值的关联程度进行组合，故预测精度也较好;方案2中，组合预测结果受单项预测残差的影响最大。比较方案1～4中RBF单项预测模型的权值发现，前3类组合预测中均赋予RBF较大的权值，方案4中RBF权值最小。事实上，就单项预测而言，RBF预测效果最好，方案4将其赋予较小的权值，和实际不符，所以其预测效果最差。

5 结论

1)在变形并联组合模型的构建中，权重求解约束条件的选取是其关键所在;

2)不同约束准则下，单项模型的权值存在较大的差异，此种差异是对约束准则特点的具体反映;

3)神经网络的非线性定权法是一种较好的定权方式，具有良好的预测效果;

4)并联组合预测模型构建中，单项预测模型出现的负权情况，是否即可认为该单项预测模型的预测结果无效及其预测结果的意义等问题，需进一步深入研究。

1 潘国荣，谷川.形变监测数据组合预测［J］.大地测量与地球动力学，2006(4):27 － 29.(Pan Guorong，Gu Chuan.Combination prediction of deformation monitoring data［J］.Journal of Geodesy and Geodynamics，2006(4):27 －29)

2 高宁，崔希民，高彩云.顾及模型误差补偿的GM(1，1)变形预测建模［J］.大地测量与地球动力学，2012(5):99－102.(Gao Ning，Cui Ximin，Gao Caiyun.Optimal method for GM(1，1)modeling for prediction of deformation taking compensation for model errors into acount［J］.Journal of Geodesy and Geodynamics，2012(5):99 － 102)

3 曹洋兵，晏鄂川，谢良甫.考虑环境变量作用的滑坡变形动态灰色-进化神经网络预测研究［J］.岩土力学，2012，33(3):847 － 852.(Cao Yangbing，Yan Echuan，Xie Liangfu.Study of landslide deformation prediction based on gray model-evolutionary neural network model considering function of environmental variables［J］.Rock and Soil Mechanics，2012，33(3):847 － 852)

4 吴益平，滕伟福，李亚伟.灰色-神经网络模型在滑坡变形预测中的应用［J］.岩石力学与工程学报，2007，26(3):632 － 636.(Wu Yiping，Teng Weifu，Li Yawei.Application of grey neural network model to landslide deformation prediction［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26(3):632 － 636)

5 高宁，崔希民，高彩云.高层建筑物沉降变形的灰线性预测［J］.测绘科学，2012，37(3):96 － 98.(Gao Ning，Cui Ximin，Gao Caiyun.Application of GM(1，1)and line regression for predicting subsidence and deformation of high building［J］.Science of Surveying and Mapping，2012，37(3):96－98)

6 高宁，崔希民，高彩云.灰时序GM-AR模型在建筑物沉降变形预测中的应用［J］.测绘科学，2013，38(1):139－141.(Gao Ning，Cui Ximin，Gao Caiyun.Application of greytime series combined model in subsidence deformation prediction［J］.Science of Surveying and Mapping，2013，38(1):139－141)

7 高宁，高彩云.变形监测数据组合预测的串联与并联模式研究［J］.大地测量与地球动力学，2013，33(3):116－120.(Gao Ning，Gao Caiyun.On model and forecast of deformation monitoring data based on series and parallel combination prediction［J］.Journal of Geodesy and Geodynamics，2013，33(3):116 －120)

8 韩冬梅，牛文清，杨荣.线性与非线性最优组合预测方法的比较研究［J］.情报科学，2007，25(11):1 672 －1 678.(Han Dongmei，Niu Wenqing，Yang Rong.The comparative study on linear and non linear optimal forecast combination methods［J］.Information Science，2007，25(11):1 672 －1 678)

9 刘思峰，等.灰色系统理论及其应用(第五版).［M］.北京:科学出版社，2010.(Liu Sifeng，et al.Grey system theory and its application［M］.Beijing:Science Press，2010)

10 王新洲，等.高等测量平差［M］.北京:测绘出版社，2006.(Wang Xinzhou，et al.Advanced surveying adjustment［M］.Beijing:Surveying and Mapping Press，2006)

STUDY ON DEFORMATION PARALLEL COMBINATION PREDICTION UNDER DIFFERENT RESTRICTION CRITERION

Gao Caiyun1，2)，Cui Ximin1)and Gao Ning2)
1)College of Geoscience and Surveying Engineering，China University of Mining and Technology，Beijing 100083
2)Geomatics＆ City Spatial Information School，Henan University of Urban Construction，Pingdingshan467036

The parallel combination deformation prediction models were studied.According to the weighted constraint criterion，five kinds of deformation parallel combination prediction models were established，including suboptimal weight combination，optimal weigh combination，synthesis relational grade of grey-weight，entropy-weight and artificial neural network-weight.Based on the characteristics of the models，the effects of parallel combination prediction under different constraint criterion are compared.The results of analysis with real data show that the nonlinear combination prediction based on neural network is the best one.

deformation;parallel combination;restriction criterion;weight;combination prediction

P258

A

1671-5942(2014)03-0091-04

2013-12-16

国家自然科学基金项目(41071328)。

高彩云，女，1980年生，博士研究生，讲师，研究方向:精密工程变形监测与灾害预报。E－mail:gaocaiyungao@163.com。