爆胎对牵引火炮行驶性能仿真分析

向飞飞，陈学军，孙华刚，楼红伟

（1．军械技术研究所，石家庄 050003；2．军械工程学院，石家庄 050003）

轮胎是火炮重要组成部分之一，主要是对火炮起支撑作用，与路面进行接触，缓和火炮在牵引过程中受到的冲击。轮胎性能的好坏直接影响着火炮性能的发挥，轮胎的结构和材料又影响着轮胎的使用性能和行驶性能。目前充气轮胎应用较为普遍，充气轮胎重量轻，行驶速度快，生热低，但是普通充气轮胎战场防护性还有待提高，一旦刺穿胎冠或击破胎体，轮胎立刻无法使用，严重影响火炮的机动性能。通过将无内胎子午线充气轮胎和实心轮胎简单技术融合，能从一定程度上综合解决火炮机动能力和防弹问题，但却无法改变实心轮胎不能兼顾高速公路和泥泞路面的弊端。因此，国外通过采用在宽断面低压轮胎中加装支撑体技术，研发了用于轮式火炮内支撑轮胎。其基本原理是在轮胎部分或全部漏气而失去控制时支撑和火炮的重量，通过在蜂窝状的气室里充上高压惰性气体，用以提高支撑体的负载能力和轮胎跑气后的火炮行驶平顺性［1］。目前对轮胎性能的研究比较多，如文献［2－3］针对单个轮胎进行有限元仿真分析，得到其自身的机械特性；文献［4－6］对轮式车辆进行动力学仿真分析，得到路面对车辆的影响分析。本文在继承前人的工作之上，对内支撑轮胎进行有限元分析和动力学仿真，掌握火炮在行驶过程中爆胎对火炮的影响，并与传统充气轮胎进行对比分析。

1 内支撑轮胎理论模型

近年来，内支撑轮胎发展迅速，并日益成为主流产品。其中较为典型的是米其林公司的PAX轮胎，其中支撑体的主要类型有：多功能支撑体、防地雷多功能支撑体、多气室橡胶支撑体、充气橡胶支撑体、复合材料支撑体以及滚动支撑体等。本文分析的轮胎支撑体为多气室橡胶支撑体。

火炮在牵引行驶过程中，轮胎与地面接触，轮胎的机械特性对火炮的牵引过程影响很大。轮胎动力学的研究包括从稳态到非稳态和从线性到非线性两个过程。轮胎动力学模型分为理论模型、经验模型、半经验模型和自适应模型4类［3］。笔者使用的是轮胎理论模型中的Fiala模型，该模型是在简化的轮胎物理模型的基础上建立的，如图1所示。

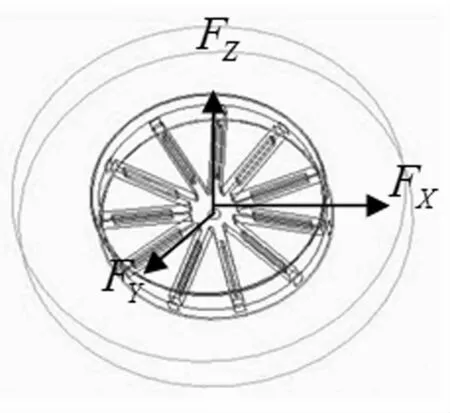
图1 轮胎受力图Fig．1 The force of tire

1.1 轮胎垂直力

火炮轮胎的垂直力主要是由轮胎垂直刚度和垂直阻尼引起的。垂直力计算如下：

式中，FZK是轮胎垂直刚度引起的垂直力，FZC是轮胎垂直阻尼引起的垂直力。

式中，K是轮胎垂直刚度，δ是轮胎偏转穿透系数。

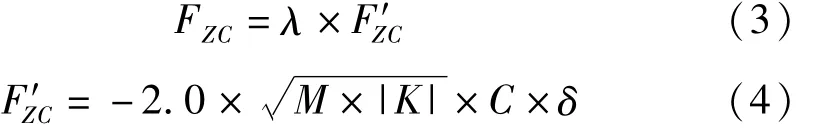
式中，M是轮胎的质量，C是轮胎垂向阻尼系数。

其中λ是穿透函数等级。

1.2 轮胎纵向力

火炮轮胎在运动过程轮胎会发生弹性变形，产生轮胎纵向力。在滑动阶段：

滑移系数

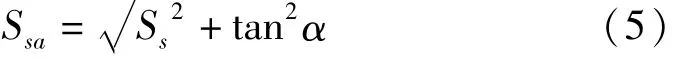
纵向滑移阈值

弹性变形阶段：时

滑移阶段

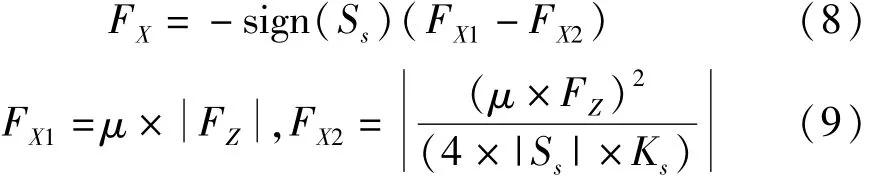
式中，FZ是垂直力，μ是摩擦系数，Ss是纵向滑移，α是滑移角，Ks是轮胎纵向刚度。

1．3 轮胎侧向力

当轮胎处于弹性变形阶段时：β≤β*

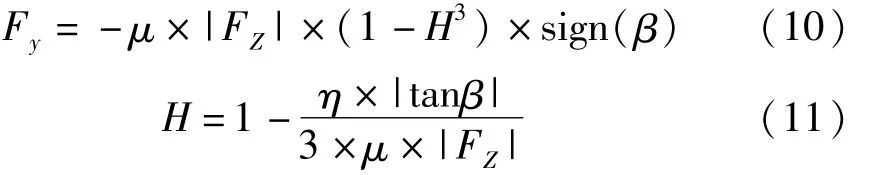
当轮胎处于滑移阶段时：β＞β*

式中，β是侧偏角，β*是侧偏角阈值，η是侧偏刚度系数。

2 火炮牵引模型的建立

2.1 轮胎模型

在动力学仿真过程中轮胎作为火炮运动过程中非常重要的部件之一，如何选择符合仿真和实际的轮胎模型是关键。内支撑轮胎与普通充气轮胎在结构和材料选用上都有着明显的区别，内支撑轮胎外胎是全钢子午线轮胎，内部还有内支撑体，而充气轮胎外胎是斜交轮胎，内部就一个充气内胎。为了得到较为准确的仿真结果，本文采用Fiala轮胎模型作为动力学仿真实验的轮胎模型，定义Fiala轮胎模型与路面接触面为矩形，接触力均匀分布在接触面上。通过性能测试实验得到了仿真过程中所需的轮胎相关参数值如表1所示。

表1 轮胎参数Tab．1 Tire parameters

表2 轮胎爆胎后参数Tab．2 Tire parameters after flat

在仿真过程中轮胎发生爆胎时其自身参数会发生变化，对轮胎爆胎的机理也是目前的难点，本文在将爆胎过程理想化瞬间完成，只考虑其自身参数变化，通过参考文献7中建立了轮胎爆胎模型，对内支撑轮胎和普通充气轮胎爆胎后其参数变化情况进行了计算，计算结果如表2所示。

2.2 路面模型［8］

路面激励对火炮行驶过程有着重要的影响。本文路面模型参照国家标准《路面不平度表示方法草案（ISO／TC108／SC2N67）》与国家标准 GB7031－86《车辆振动输入－路面平度表示方法》中路面分类标准，根据某一等级路面不平度系数Gq（n0）的取值，采用有限个离散空间频率nk的三角级数确定路面不平度q（l），再将q（l）输入路面生成软件中，得到所需要的等级路面。

式中，ak为路面幅值，l为路面里程，βk为相角，在0～2π之间随机分布变量，n为空间频率，n0为参考频率，Gq（n0）路面谱值，W为频率指数，nku、nk1为空间频率的上下限频率。在RecurDyn中建立的C级路面如图2所示。

图2 C级路面模型Fig．2 The model of road

2．3 牵引火炮模型

RecurDyn提供了一些建模模块，可以建立结构相对简单的模型，还提供了CAD软件接口，方便模型的导入，但其建模功能远不如PRO／E软件强大。本文利用PRO／E建立某型牵引火炮行驶模型如图3所示。模型包括：火炮模型、牵引车模型和路面模型。其中火炮模型包括：身管、摇架、上架、防盾、大架和缓冲器等部件。考虑计算机仿真速度和仿真效果，在不改变牵引车动力学特性的前提下进行了合理简化，缩短仿真计算的时间，减少工作量。具体简化方法如下［6］：

（1）研究火炮在牵引过程中的稳定性，将牵引车车体简化为一个刚体；

（2）各连接件及螺栓在仿真过程中对仿真结果影响不大，全部省略；

（3）各部件之间没有相对运动，摩擦力忽略不计；

（4）不考虑驾驶员对牵引车的行驶速度影响，速度保持恒速；

（5）忽略空气阻力对模型的影响。

为了提高计算精度，将省略的零件质量平均加到各部件上。

火炮牵引模型主要包括牵引车和火炮主体。为了研究火炮轮胎对火炮行驶稳定性的影响，将牵引车进行了简化，牵引车包括：转向系统、悬挂系统和操纵系统。火炮模型包括：左右两个轮胎，左右两个扭力杆（悬挂），火炮身管，其他部分作为一个刚体。火炮牵引模型如图3所示。

图3 牵引火炮三维模型Fig．3 The model of artillery traction

3 仿真试验

轮胎发生故障情况比较多，如气压不足、下沉量过大，都会对火炮行驶性能产生较大影响，极限情况为爆胎，本文主要考虑爆胎对行驶性能的影响。在仿真过程中假设牵引车驱动轮同步转动，扭矩均匀，爆胎是个短暂的过程，理想看成为在瞬间完成爆胎。

3.1 轮胎结构对行驶性能的影响

在仿真开始时，火炮模型在重力的作用下，与路面接触，达到力平衡，这一过程会对仿真造成影响。为解决这一问题，在RecurDyn中使用阶跃函数来控制速度，其调用格式为 STEP（Time，0，0，0．3，v），其中 v为火炮行驶速度。对火炮行驶过程进行动力学仿真，设置仿真时间为15 s，步长为500，在C级路面上以60 km／h的速度行驶，其中仿真过程用到的充气轮胎和内支撑轮胎参数已在表1和表2中列出。

通过对火炮行驶过程发生爆胎动力学仿真分析，得到使用不同轮胎爆胎后火炮侧偏位移、侧向加速度和纵向加速变化规律，如图4～6所示。

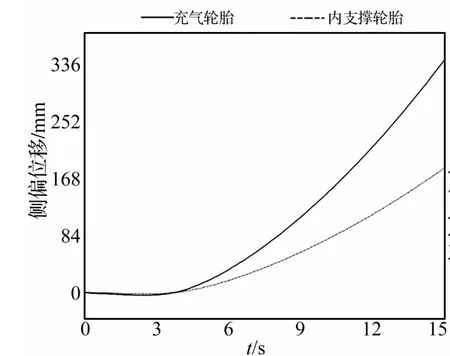
图4 侧偏位移曲线Fig．4 The curve of lateral displacement

图5 侧向加速度曲线Fig．5 The curve of lateral acceleration

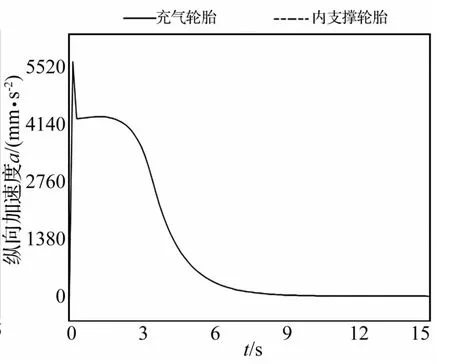
图6 纵向加速度曲线Fig．6 The curve of longitudinal acceleration

根据火炮行驶过程中爆胎后的运动曲线可以看出：

（1）内支撑轮胎发生爆胎后，内支撑体支撑火炮的重量，具有一定的缓冲能力，可以改善轮胎爆胎后行驶性能，在侧偏性能方面较传统充气轮胎有所改善。

（2）由于轮胎爆胎后，轮胎与地面的接触材料和参数均有所变化，致使充气轮胎爆胎引起的侧向加速大于内支撑轮胎引起的火炮侧向加速度。

（3）火炮在行驶过程中爆胎会引起纵向加速度，两种轮胎产生的纵向加速度变化规律一致。

3.2 行驶速度对行驶稳定性的影响

设置仿真时间15 s，步长500，火炮分别以30 km／h、60 km／h、80 km／h的速度行驶，模拟火炮行驶过程中爆胎，结果如图7～9所示。

图7 侧向位移曲线Fig．7 The curve of lateral displacement

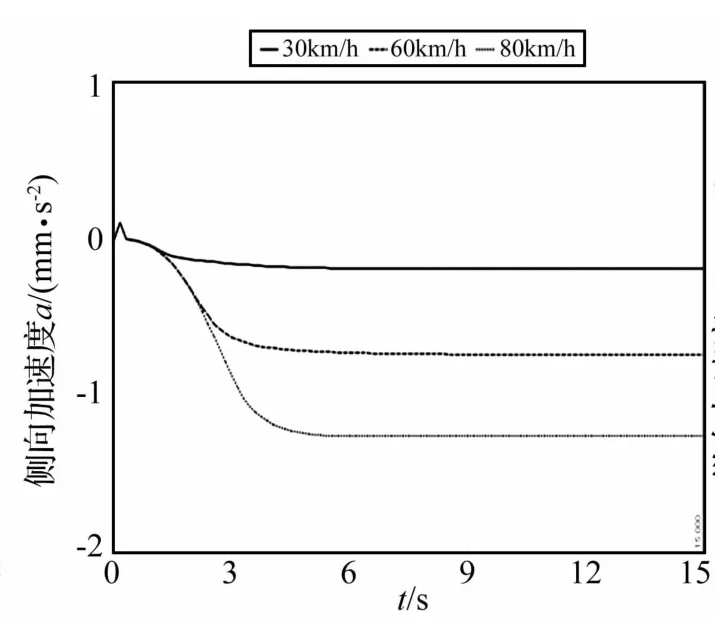
图8 侧向加速度曲线Fig．8 The curve of lateral acceleration

图9 纵向加速度曲线Fig．9 The curve of longitudinal acceleration

由图7～9可以得到：侧偏位移随着行驶速度的增大而增大，行驶速度对侧向加速度纵向加速度影响不明显。

3．3 实路试验

为了验证仿真结果的可靠性，本文做了一些相应的试验来验证。由于这个实路试验存在一定不安全因素，本文将试验进行了一些简化。在实验过程中，在确保人员和车辆安全的前提下，在兵器试验基地进行火炮牵引过程中发生爆胎试验，如图10所示。

图10 火炮牵引试验Fig．10 The test of artillery test

通过试验结果来看，建立的仿真模型是正确的，虚拟仿真是有效的。由于模型中进行了大量简化，为考虑驾驶员对车辆的控制和驾驶熟练程度，与实际还是存在一定误差。

4 结 论

本文通过对火炮行驶过程的仿真分析，模拟了火炮在行驶过程中发生爆胎，对危险系数大的火炮牵引试验提供了理论指导，仿真结果与基地试验结果基本吻合，验证了模型的正确性，对火炮的行驶性能试验和行驶安全性分析提供了参考。

［1］杨欣，佟金，陈东辉等．RFT内支撑三维结构有限元静力学分析与改进［J］．农业机械学报，2008（3）：10－13．YANG Xin， TONG Jin， CHEN Dong-hui， et al． Finite element analysis on three dimensional struct-ural of run flat tire insert［J］．Transactions of the Chinese Society for Agricultural Machinery，2008（3）：10－13．

［2］倪天心，左曙光，吴佩等．轮胎稳态滚动的仿真及其接地面积的可视化测量［J］．汽车工程学报，2011（9）：407－414．NI Tian-xin，ZUO Shu-guang，WU Pei，et al．Simulation and visualized measuring of the contact area of a steady-rolling tire［J］．Chinese Journal of Automotive Engineering，2011（9）：407－414．

［3］方杰，吴光强．轮胎机械特性虚拟试验场［J］．计算机仿真，2007：243－247．FANG Jie，WU Guang-qiang．Virtual proving ground of tire mechanical characteristics［J］．Computer Simulation，2007：243－247．

［4］生龙波，马吉胜，李涛，等．某型履带车辆紧急制动动力学仿真分析［J］．火炮发射与控制学报，2012（3），14－17．SHENG Long-bo，MA Ji-sheng，LI Tao，et al．Emergency braking dynamic simul-ation analysis of a certain tracked vehicle［J］．Journal of Gun Launch＆Control，2012（3）：14－17．

［5］贾进峰，张进秋，毕占东，等．轮式装甲车辆越野路面平顺性评价及试验研究［J］．车辆与动力技术，2011（2）：46－51．JIA Jin-feng，ZHANG Jin-qiu，BI Zhan-dong，et al．Ride comfort evaluation and experim-ent of a wheeled armored vehicle on off-road terrain［J］．Vehicle＆Power Technology，2011（2）：46－51．

［6］向涛波，刘重发，赵俊，等．某型自行火炮行驶平顺性仿真研究［J］．机械设计与制造，2011（10）：220－222．XIANG Tao-bo，LIU Zhong-fa，ZHAO Jun，et al．Modeling and simulation on ride comfort of a self-propelled gun［J］．Machinery Design＆Manufacture，2011（10）：220－222．

［7］周景宇，爆胎汽车建模与稳定性控制［D］．长沙：湖南大学，2012：7－31．

［8］徐中明，周小林，余烽，等，汽车平顺性分析时域法和频域法的对比［J］．汽车工程，2012（34）：306－310．XU Zhong-ming， ZHOU Xiao-lin， YU Feng， et al．Comparison between time and frequency domain method in vehicle ride comfort anal-ysis［J］．Automotive Engineering，2012（34）：306－310．