基于SPH-FEM 耦合算法的磨料水射流破岩数值模拟

林晓东，卢义玉，汤积仁，敖 翔，张 磊

（1．重庆大学 煤矿灾害动力学与控制国家重点实验室，重庆 400030；2．重庆大学 复杂煤气层瓦斯抽采国家地方联合工程实验室，重庆 400030）

磨料水射流是磨料与高速流动的水，或者与高压水互相混合而形成的液固两相介质射流，因其切割破碎作业效率高、作业过程没有热反应区、不发生化学反应等优点，被广泛运用在石油化工、机械加工、采矿、隧道开挖等行业中［1－4］。尤其在岩石破碎领域，文献［5］提出磨料水射流联合机械破碎硬岩方法，取得了较好的效果。在该方法中磨料水射流除了冲蚀去除岩石外，其对冲孔周边岩石的损伤对后续的机械破岩具有重要意义。

磨料射流破岩是一个涉及诸多因素的非线性冲击动力学问题，具有瞬时强值动载荷、大变形及高应变率等特点。受现有理论研究能力和试验条件的限制，利用理论方法或实验手段进一步探索磨料射流冲蚀损伤破岩机理的难度非常大。然而，随着计算机技术和计算理论的发展，可以运用数值模拟计算手段对上述问题进行分析研究，这一方法已在大量复杂问题的求解中取得成功。孙清德等［6］运用动态非线性有限元法和Hoffman破碎准则对高压水射流破岩规律进行了模拟，认为提高射流冲击速度、喷射直径、横移速度、射流束数，在35°至40°之间合理选择射流入射角可以提高射流破碎岩石的效率；宋祖厂等［7］运用SPH算法模拟了高压水射流破岩过程，针对水射流破岩能量转化、水射流冲击力、水力破岩演化进行了分析；卢义玉等［8］运用SPH算法模拟了脉冲水射流破岩过程中的应力波效应，得到了不同岩性岩石在脉冲射流应力波作用下的破坏形式；刘佳亮等［9］运用ALE算法对高压水射流冲击高围压岩石的损伤演化过程进行了数值模拟，认为围压对岩石轴向损伤影响较大径向损伤影响较小。以上模拟方法，主要是针对高压水射流的模拟。Kumar等［10］应用有限元法分析了单颗磨料粒子以不同角度冲击钛合金的损伤机理；王明波等［11－12］应用动态非线性有限元法对单颗粒磨料冲击岩石破岩效果进行了模拟并对其破岩过程和破岩机理进行了分析，该方法没有考虑到冲蚀过程是连续的磨料粒子的作用，同时也忽略了水的贡献。Anwar等［13］应用有限元法模拟了磨料粒子束磨损Ti6Al4V材料的过程，并研究了磨痕的形成机理，但该方法忽略的水的作用。司鹄等［4］采用ALE流－固耦合罚函数算法模拟了磨料水射流破煤岩的过程，但只定性地分析了岩石的损伤场，并未对损伤范围进行量化。

本文采用SPH-FEM耦合算法，将模型考虑成混有磨料的水柱与岩石作用，磨料水射流用SPH模拟，岩石采用Lagrange有限元模拟，充分考虑磨料和水对岩石的共同作用，与真实情形更加接近。数值模拟模拟磨料水射流冲击作用下岩石冲蚀坑的形成过程，并研究岩石破碎坑周围的损伤范围。

1 SPH-FEM耦合算法

磨料水射流冲蚀损伤破岩过程中，高速射流出现高压和大变形问题，采用传统的拉格朗日法模拟磨料水射流容易出现网格畸变而导致计算终止［14］。SPH算法不使用单元，而是使用固定质量的可动点，所以没有网格畸变。但是SPH方法相比拉格朗日法其计算精度不高，因此岩石采用FEM模拟，能够得到相对准确的损伤特性。SPH-FEM耦合算法既可以很好的模拟瞬间大冲击、大变形、高应变率等问题，又克服了SPH计算精度低的问题。

1.1 SPH基本理论

SPH方法的基础是插值理论［15－17］。在SPH中任一宏观变量都能方便的借助于一组无序点上的值表示成积分插值计算得到。核近似函数为：

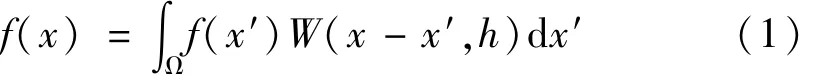
式（1）中，f（x）为三维坐标向量 x的函数；Ω为点 x的支持域；x－x′为粒子间距离；h为SPH粒子的光滑长度，光滑长度随时间和空间变化；W（x－x′，h）为核函数通常使用辅助函数θ（x－x′）进行定义，即

式（2）中，d为空间维数。

SPH中最常用的光滑核是三次B样条曲线，即

式（3）中，C为归一化常量，由空间维数确定

联系式（1）（2）用粒子近似方法将连续形式的积分方程转换成离散型的方程形式为：

式（4）中，ρi为粒子 i的密度；mi为位于 i处的粒子质量。

1.2 SPH-FEM耦合处理

SPH粒子在LS-DYNA中被视为特殊的节点单元，控制参数为节点编号、质量以及空间位置［14］。SPH粒子与FEM耦合通过罚函数方式将质点的力作用于有限元单元表面，因此SPH-FEM耦合采用点面接触的接触方式。在本文SPH与FEM耦合处理中，将SPH粒子定义为从节点，将与SPH粒子接触界面上的有限元单元表面定义为主面。接触耦合算法如图1所示［18］。

图1 SPH-FEM耦合算法Fig．1 Coupling algorithm of SPH-FEM

2 计算模型描述

为了对问题进行一定的简化，在建立模型之前作如下假设：①磨料水射流破岩过程仅仅涉及水、磨料、岩石三种物质；②水粒子与磨料粒子为等直径的球体；③磨料粒子随机分布在水粒子之间，磨料粒子与水粒子具有相同的速度；④岩石为连续介质体，忽略孔隙介质的影响。

2.1 磨料水射流模型

磨料水射流破岩过程中，水、磨料均采用SPH算法模拟，在LS-DYNA中采用NULL材料模型，并对水、磨料材料模型赋予 Mie-Grueisen状态方程（式（5）），其中磨料选用陶粒。水与磨料本构模型参数见表1。

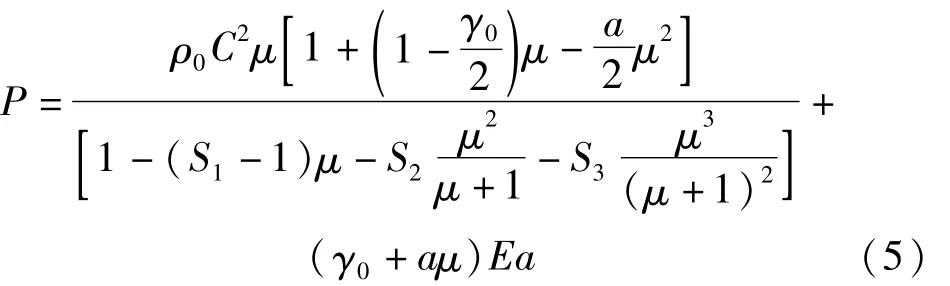
式（5）中，E是单位体积内能，C是vs－vp曲线的截距，s1、s2和 s3是 vs－vp曲线的斜率系数，γ0是 Mie-Grueis-en常数，a是一介体积修正量。

表1 水、磨料本构模型参数Tab．1 Parameters in M ie-Grueisen equation of state for water and abrasive

磨料水射流包含水与磨料两种成分，如何实现磨料与水两种成分的随机混合是磨料水射流建模的关键。本文按照如下思路建立磨料水射流模型：

第一步，根据磨料水射流中磨料的质量浓度α确定磨料水射流中磨料与水的体积比β。

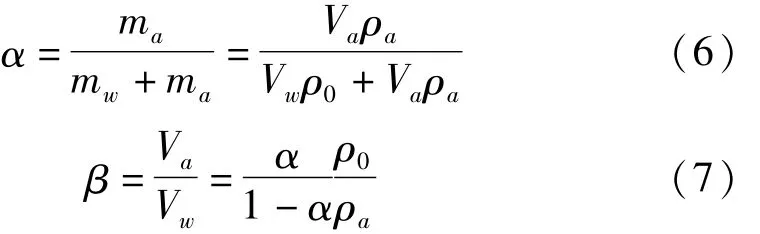
式（6～7）中，ma、mw分别为磨料水射流中磨料与水的质量；Va、Vw分别为磨料水射流中磨料与水的体积；ρa、ρ0分别为磨料水射流中磨料与水的密度。

第二步，根据假设建模所用的水粒子与磨料粒子为等直径的球体，则由二者的体积比β可以确定出二者的个数比γ。

式（8～9）中，na、nw分别为磨料水射流模型中磨料粒子与水粒子的个数；d为磨料粒子与水粒子的直径。

第三步，根据磨料水射流冲蚀靶距处的射流宽度（直径）D［19］，确定单层模型直径上的粒子的总数 Nd，LS-DYNA软件由Nd便确定了单层SPH粒子总数Ns；根据模拟的需要确定磨料水射流模型长度L，确定模型层数Nc，确定SPH粒子总数N。

式（10）中，D0为磨料喷嘴出口直径；x为沿轴向距喷嘴出口的距离，即靶距。

第四步，确定SPH粒子总数后，根据磨料粒子与na水粒子个数比γ确定磨料水射流模型中磨料粒子数量与水粒子的数量nw。

第五步，利用EXCEL程序随机抽样命令从SPH粒子中抽取数量为na的样本，对其赋予磨料粒子的属性，剩余的nw个粒子赋予水粒子的属性。

第六步，将磨料粒子和水粒子的信息写入 LS-DYNA关键字文件中，完成磨料水射流建模。

2.2 岩石模型

岩石采用H－J－C材料模型。由于H－J－C材料模型等效屈服强度是拉力、压力、应变率及损伤的函数，而拉力和压力是体积应变的函数，损伤累积是塑性体积应变、等效应变、拉力及压力的函数，所以能够满足大变形、高应变率、高拉压效应的岩石工况［20－21］。

H－J－C模型的强度模型以规范化等效应力描述：

损伤因子通过等效塑性应变和塑性体积应变累积得到：

式（14～15）中，σ*T／fc；σ为等效应力，σ*≤SMAX，SMAX为材料所能承受的最大强度；P为单元内的静压；T为材料的最大拉伸强度；ε·为应变率；ε0为参考应变率；fc为材料的抗压强度；A、B、C、N、D1、D2为材料常数；D为损伤度（0＜D＜1），且 D1（P*＋T*）D2≥EFMIN，EFMIN为材料的最小断裂应变；Δεp和Δμp分别代表在一个积分步长内单元的等效塑性应变和塑性体积应变。单元的变形分为抗压和拉伸两种情况。岩石的本构模型参数见表2，其中岩石材料为灰岩。

表2 灰岩的本构模型参数Tab．2 H－J－C parameters of limestone

2．3 几何模型及边界条件

根据以上建模方法建立如图2所示几何模型，由于磨料水射流破岩过程基本是轴对称的，为了简化计算，本次数值模拟建立1／4模型［4］。磨料水射流为Ф4 mm×70 mm的1／4圆柱体，并对对称面采用 SPH＿SYMMETRY＿PLANE对称约束。岩石模型的几何尺寸为25 m×25 mm×25 mm，为了模拟岩石无限大的工况，对模型底面和外围两个面采用NON＿REFLECTING非反射约束，对称面采用CONSTRAINED＿GLOBAL对称约束。磨料水射流模型包含1 680个SPH粒子，其中磨料粒子（红色）153个，水粒子（蓝色）1 527个，岩石模型包含288 000个六面体有限元。

图2 磨料水射流破岩模型Fig．2 Themodel of abrasive water jet breaking rock

3 计算结果分析

根据所述的建模方法对磨料水射流破岩过程进行模拟。图3给出了速度为250 m／s、磨料浓度30%的磨料水射流破岩效果图。

3.1 冲孔形态分析

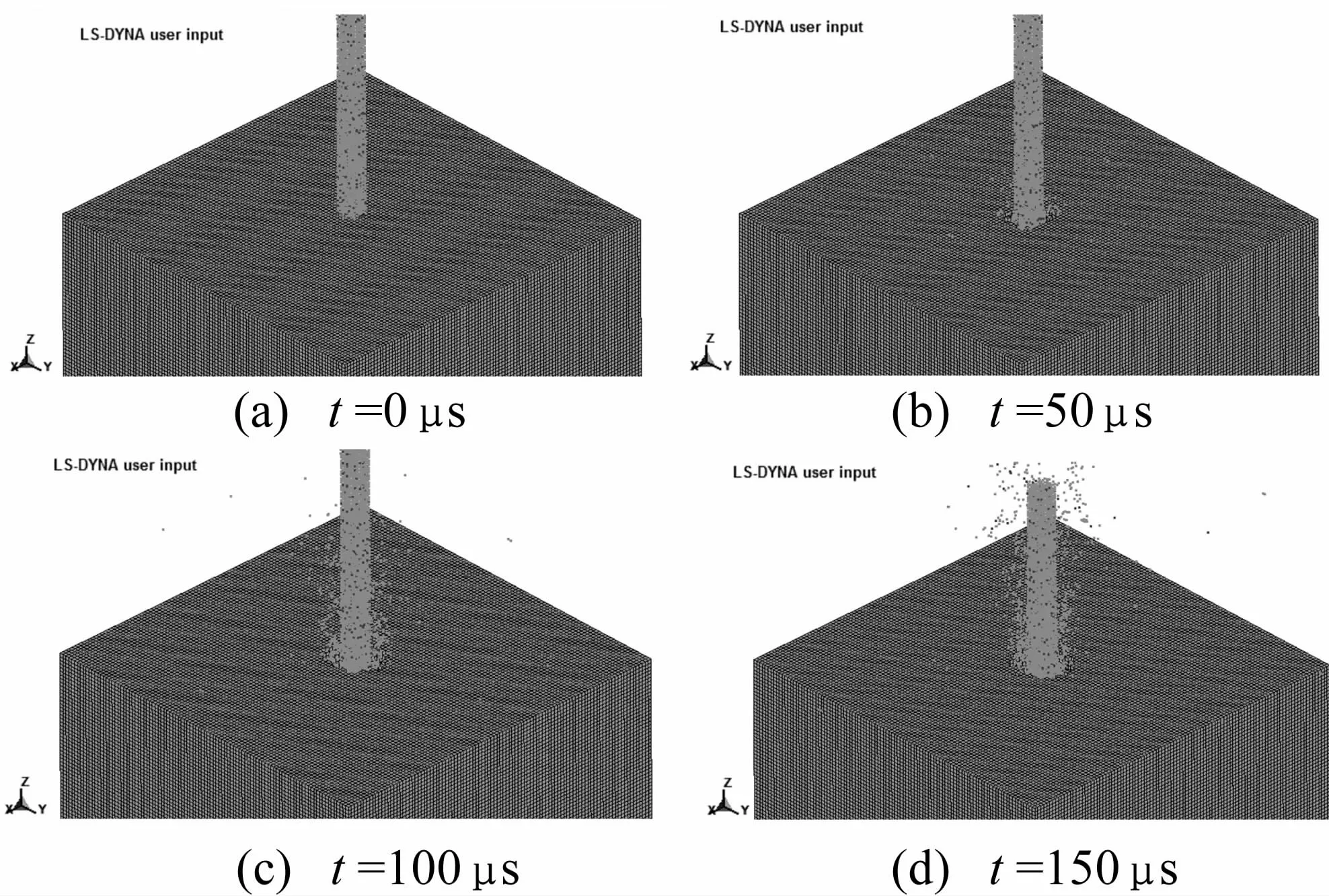
图3 磨料水射流破岩效果图Fig．3 Effect picture of abrasive water jet breaking rock

图4为射流速度250 m／s、磨料浓度30%不同时刻岩体冲蚀坑截面形状演化图。冲蚀坑形态的演化之所以会如图4中所示，主要是因为：磨料水射流与岩石发生接触，首先在冲蚀作用中心区域的岩石单元迅速破坏失效并删除，形成初始孔径，随着冲蚀过程的延续，一部分粒子继续加深冲蚀深度，与此同时与孔底撞击后向周围发散飞溅的另一部粒子对初始孔孔壁岩体进行冲蚀并扩大孔径——扩孔，这便形成了“V”形剖面；但是用于扩孔的粒子能量低，孔径很快便趋于稳定，随着时间的进程，在冲蚀坑孔径相对稳定的情况下深度却在不断增加，便形成了由成“V”形剖面和圆形截面组成的“子弹”体，如图4（d）所示，与图5实验中冲孔形态ICT扫描结果以及文献［9，22］中的结果均吻合较好，表明本文建立的磨料水射流冲蚀损伤岩石模型是正确可行的，可用于后续的磨料水射流破岩损伤特性的研究。

图4 冲蚀坑截面形状演化图Fig．4 Evolution chart of erosion pit sectional shape

图5 冲孔形态ICT扫描实验结果图Fig．5 Results of ICT scanning experiment

3.2 岩石损伤分析

磨料水射流破岩是一个“冲蚀－损伤－冲蚀－损伤……”交替进行的动态过程。磨料粒子对岩石表面的冲击作用，在岩石中形成由径向－中间裂纹和侧向－扩展裂纹构成的裂纹系统，其中侧向－扩展裂纹向岩石自由表面扩展，实现岩石的宏观破碎，形成冲蚀坑，而径向－中间裂纹则部分残留于岩石之中，造成对冲蚀坑周围岩石的损伤［23］。在磨料水射流联合钻头钻进的技术中，岩石冲孔后的损伤范围尤其是冲蚀坑径向损伤范围对后续的机械岩石破碎影响重大。图6给出了岩石在速度250 m／s磨料浓度30%磨料水射流冲蚀下不同时刻的宏观损伤云图。

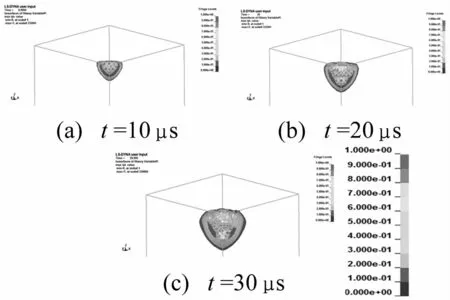
图6 岩石损伤变量D分布图Fig．6 Distribution of damage variable D in rock

为了对磨料水射流冲蚀损伤范围进行量化，如图7所示，在X－Z剖面上从距岩石顶端自由面深4 mm距轴线4．5 mm处沿径向方向由内及外依次选取相邻的17个单元作为跟踪测量点，给出各单元损伤值随时间变化曲线，并绘制t＝200μs时刻各单元损伤值随距离变化曲线。由图8～9可知在磨料水射流冲蚀作用下处于冲蚀坑范围内单元A损伤值迅速达到1并完全失效；由于冲蚀能量的衰减剧烈，处于冲蚀坑外的单元由内到外损伤值迅速下降，距离轴线足够远的单元K损伤值为0并未受到损伤，其余各单元均有不同程度的损伤。由此可以得出：① 单元A与单元B的交界面即为冲蚀坑的孔壁，其距冲孔轴心O的距离即为冲孔半径，冲孔半径约为0．45 cm；② 单元J与单元K的交界面即为冲蚀损伤区外边界，损伤半径约为0．90 cm。

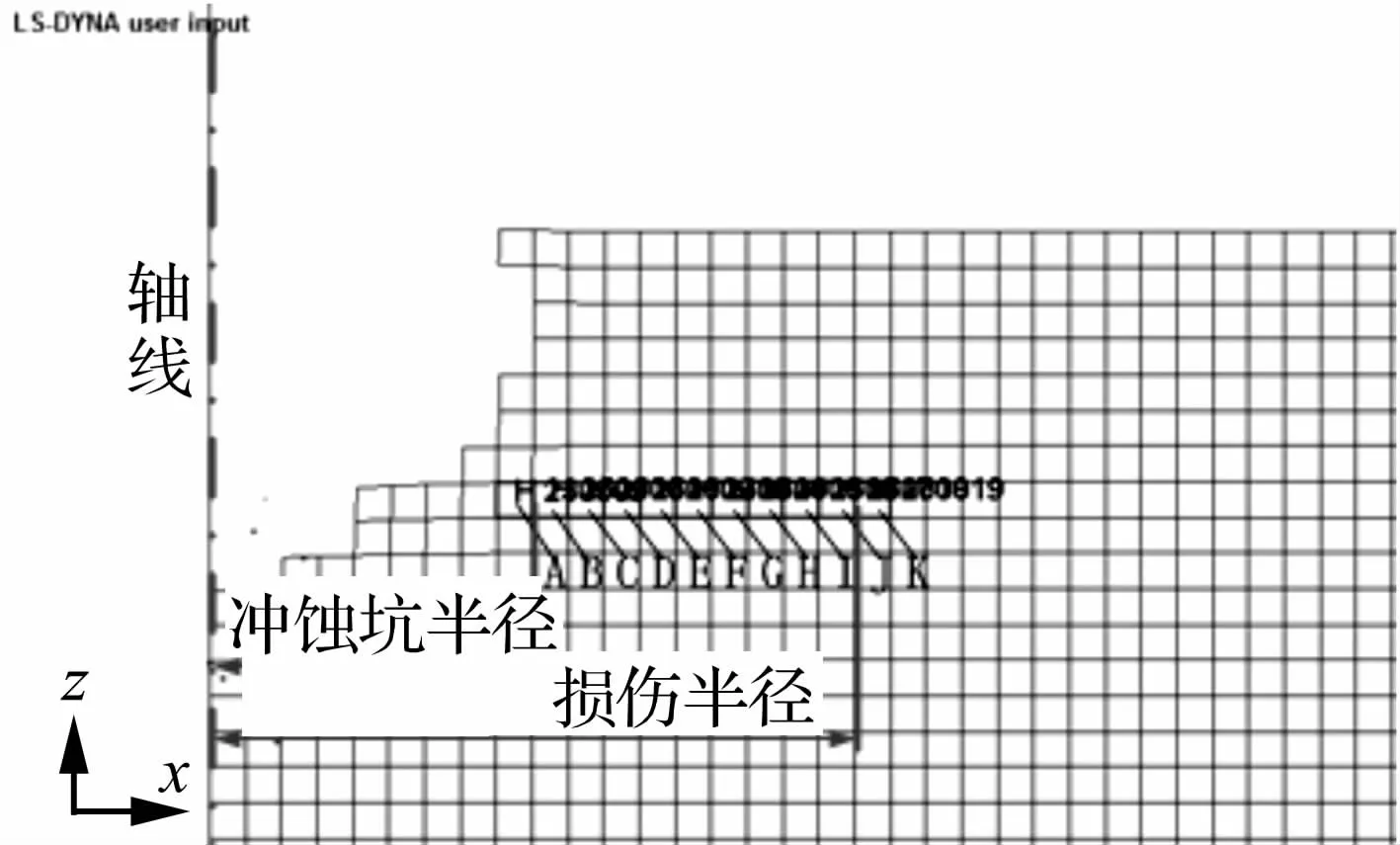
图7 X－Z剖面单元选取示意图Fig．7 Schematic view of selected units in the X－Z cross-section

图8 损伤因子D随时间的变化关系Fig．8 D evolution with time

图9 损伤因子D随距离的变化关系Fig．9 D evolution with distance

按照上述方法模拟了浓度30%不同速度的磨料水射流冲蚀岩石，表3为不同速度磨料水射流作用下的冲蚀坑半径和损伤半径。由表3可知磨料水射流作用下岩石的损伤半径与冲蚀坑半径随着射流速度减小而减小，两者之比在1．8－2．2之间。

表3 不同速度磨料水射流作用下岩石损伤、冲蚀坑半径Tab．3 Rock dam age，erosion pit radius under the action of abrasive water jet at different speeds

4 结 论

（1）针对磨料水射流冲蚀损伤破岩过程中因为高速射流高压和大变形特征导致网格畸变而使计算终止的问题，提出SPH-FEM耦合算法，充分考虑了磨料粒子与水形成射流后共同对岩石作用的工况。磨料水射流采用SPH模拟，岩石采用FEM模拟，既解决了高速射流因为高压和大变形导致模拟计算困难的问题，又充分利用了FEM计算精度高的特性。

（2）模拟分析了磨料水射流冲蚀作用下，岩体冲蚀坑截面形状演化过程：首先在冲蚀作用中心区域形成初始孔径，进而由于磨料水射流的扩孔作用形成“V”形剖面，随着冲蚀过程的延续，冲蚀坑不断的加深，最终形成了由成“V”形剖面和圆形截面组成的“子弹”体。

（3）采用H－J－C损伤材料模型，通过定义跟踪测量点的方式研究了磨料浓度30%不同速度磨料水射流岩石的损伤范围，得到磨料水射流作用下岩石的损伤半径与冲蚀坑半径随着射流速度减小而减小，两者之比在1．8－2．2范围之间的结论。

（4）由于磨料水射流破岩作用机理复杂，实验过程透明度差，本文提出的数值模拟方法旨在为研究磨料水射流破岩提供一种研究的方法，对于不同的磨料浓度和射流速度以及不同的岩性有待今后进一步的研究。

［1］李晓红，卢义玉，向文英．水射流理论及在矿业工程中的应用［M］．重庆：重庆大学出版社，2007．

［2］牛继磊，李根生，宋剑，等．磨料射流射孔增产技术研究与应用［J］．石油钻探技术，2003，31（5）：55－57．NIU Ji-lei，LIGen-sheng，SONG Jian，etal．，Investigation and application of abrasive water jet perforation to enhance oil production［J］．Petroleum Drllng Technques，2003，31（5）：55－57．

［3］李根生，沈忠厚．高压水射流理论及其在石油工程中应用研究进展［J］．石油勘探与开发，2005，32（1）：96－99．LIGen-sheng，SHEN Zhong-hou．Advances in seorches and appliecation ofwater jet theory in peeroleum enginearing［J］．Petrcleum Exploration and Development，2005，31（5）：96－99．

［4］司鹄，谢延明，杨春和．磨料水射流作用下岩石损伤场的数值模拟［J］．岩土力学，2011，32（3）：935－940．SI Hu， XIE Yan-ming， YANG Chun-he． Numerical simulation of rock damage field under abrasive water jet［J］．Rock and Soil Mechanics，2011，32（3）：935－940．

［5］Lu Y Y，Tang J R，Ge Z L，et al．Hard rock drilling technique with abrasive water jet assistance ［J］．International Journal of Rock Mechanics and Mining Sciences．2013，60：47－56．

［6］孙清德，汪志明，于军泉，等．高压水射流破岩规律的数值模拟研究［J］．岩土力学，2005，26（6）：978－982．SUN Qing-de，WANG Zhi-ming，YU Jun-quan，et al．A disquisition on breaking mechanismof high pressure jet impacting on rock［J］．Rock and Soil Mechanics，2005，26（6）：978－982．

［7］宋祖厂，陈建民，刘丰．基于SPH算法的高压水射流破岩机理数值模拟［J］．石油矿场机械，2009，38（12）：39－43．SONG Zu-chang，CHEN Jian-min，LIU Feng． Numerical simulation for high-pressure water jet breaking rock mechanism based on SPH algorithm ［J］．Oil Field Equipment，2009，38（12）：39－43．

［8］卢义玉，张赛，刘勇，等．脉冲水射流破岩过程中的应力波效应分析［J］．重庆大学学报，2012，35（1）：117－124．LU Yi-yu，ZHANG Sai，LIU Yong，et al．Analysis on stress wave effect during the process of rock breaking by pulsed jet［J］．Journal of Chongqing University，2012，35（1）：117－124．

［9］刘佳亮，司鹄．高压水射流破碎高围压岩石损伤场的数值模拟［J］．重庆大学学报，2011，34（4）：40－46．LIU Jia-liang，SIHu．Numerical simulation on damage field of high pressure water jet breaking rock under high ambient pressure［J］．Journal of Chongqing University，2011，34（4）：40－46．

［10］Kumar N，Shukla M．Finite elementanalysis ofmulti-particle impact on erosion in abrasive water jetmachining of titanium alloy［J］．Journal of Computer and Applied Mathematics，2012，263（18）：4600－4610．

［11］王明波，王瑞和，陈炜卿．单个磨料颗粒冲击岩石过程的数值模拟研究［J］．石油钻探技术，2009，37（5）：34－38．WANG Ming-bo，WANG Rui-he，CHEN Wei-qing．Numerical simulation study of rock breaking mechanism and process under abrasive water jet［J］．Petroleum Drilling Techniques，2009，37（5）：34－38．

［12］徐依吉，赵红香，孙伟良，等．钢粒冲击岩石破岩效果数值分析［J］．中国石油大学学报（自然科学版），2009，33（5）：68－71．XU Yi-ji，ZHAO Hong-xiang，SUN Wei-liang，et al．Numerical analysis on rock breaking effect of steel particles impact rock［J］．Journal of China University of Petroleum，2009，33（5）：68－71．

［13］Anwar S，Axinte D A，Becker A A．Finite elementmodelling of overlapping abrasive water jetmilled footprints［J］．Wear，2013，303（1－2）：426－436．

［14］Wang JM，Gao N，Gong W J．Abrasive water-jetmachining simulation by coupling smoothed particle hydrodynamics／finite element method［J］．Chinese Journal of Mechanical Engineering，2010，23（5）：568－573．

［15］刘飞宏，王建明，余丰，等．基于SPH耦合有限元法的喷丸残余应力场数值模拟［J］．山东大学学报（工学版），2010，40（6）：67－71．LIU Fei-hong，WANG Jian-ming，YU Feng，et al．Numerical simulation for compressive residual stress of shot-peening based on SPH coupled FEM［J］．Journal of Shandong University（Engineering Science），2010，40（6）：67－71．

［16］吕东喜，黄燕华，唐永健，等．基于SPH算法的磨粒冲击工件表面过程数值模拟［J］．振动与冲击，2013，32（7）：169－174．LUDong-xi，HUANG Yan-hua，TANG Yong-jian，et al．Simulating process of abrasive impacting a workpiece surface based on SPH method［J］．Journal of Vibration and Shock，2013，32（7）：169－174．

［17］纪冲，龙源，方向．基于FEM-SPH耦合法的弹丸侵彻钢纤维混凝土数值模拟［J］．振动与冲击，2010，29（7）：69－74．JIChong，LONGYuan，FANG Xiang．Numerical simulation for projectile penetrating steel fiber reinforced concrete with FEM-SPH coupling alforithm［J］．Journal of Vibration and Shock，2010，29（7）：69－74．

［18］ MA Li，BAO Rong-hao，GUO Yi-mu．Waterjet penetration simulation by hybrid code of SPH and FEA［J］．International Journal of Impact Engineering，2008，35（9）：1035－1042．

［19］张运．高压水射流切割原理及其应用［J］．武汉工业大学学报，1994，16（4）：13－18．ZHANGYun-qi．High pressure waterjet cutting principle with application［J］．Journal of Wuhan University of Technology，1994，16（4）：13－18．

［20］张凤国，李恩征．混凝土撞击损伤模型参数的确定方法［J］．弹道学报，2001，13（4）：12－16．ZHANGFeng-guo，LI En-zheng．A method to determine the parameters of themodel for concrete impact and damage［J］．Journal of Ballistics，2001，13（4）：12－16．

［21］巫绪涛，李耀，李和平．混凝土HJC本构模型参数的研究［J］．应用力学学报，2010，27（2）：340－344．WUXu-tao，LIYao，LI He-ping．Research on the material constants of the HJC dynamic constitutive model for concrete［J］．Chinese Journal of Applied Mechanics，2010，27（2）：340－344．

［22］王建明，宫文军，高娜．基于ALE法的磨料水射流加工数值模拟［J］．山东大学学报（工学版），2010，40（1）：48－52．WANGJian-ming，GONG Wen-jun，GAO Na． Numerical simulation for the abrasive water jet machiningbased on the ALE algorithm ［J］．Journal of Shandong University（Engineering Science），2010，40（1）：48－52．

［23］Lawn B R，Evans A G，Marshall D B．Elastic／plastic indentation damage in ceramics：the median／radial crack system［J］．Journal of the American Ceramic Society．2006，63（9－10）：574－581．