固体火箭发动机锥形壳体外压稳定性分析①

余文学，徐秉恒，刘洪超，单 琳

(中国航天科技集团公司四院四十一所，西安 710025)

固体火箭发动机锥形壳体外压稳定性分析①

余文学，徐秉恒，刘洪超，单 琳

(中国航天科技集团公司四院四十一所，西安 710025)

通过外压屈曲计算及外压试验，研究了某固体火箭发动机锥形壳体的外压稳定性。通过外压屈曲计算，得到了壳体的外压临界载荷、屈曲失稳波形、轴向位移以及径向位移随外压载荷的变化规律。对带加强环壳体也进行了外压稳定性分析。对比计算结果发现，虽然壳体的外压承受能力较低，但加强环可有效地提高壳体的外压承载能力。之后，还分析了在加强环总长度不变的情况下，不同加强环分布形式壳体的外压承载能力，得出均布4个加强环的壳体为较优选择。壳体的外压试验所得临界外压载荷与计算结果较吻合。

壳体;外压;加强环;临界失稳载荷

0 引言

固体火箭发动机在弹射、飞行等工况下，要承受一定的外压载荷:在主动飞行段，发动机工作压强大于外压，壳体受力主要按内压考虑;在被动飞行段，发动机工作结束，壳体主要承受外压。而壳体作为主要的承力结构，其外压承载能力较低，容易发生外压失稳现象。研究外压稳定性目的在于确定临界载荷及其相应的失稳模态，以增加加强措施，提高结构的抗失稳能力［1］。

本文以固体火箭发动机大长径比、锥形、超高强度钢旋压壳体为研究对象，对其进行外压稳定性分析，得出壳体的外压稳定性的分析结论。同时，对带加强环的壳体进行外压稳定性分析，探讨了加强环对壳体的失稳形式的影响。之后就试验结果和模拟结果进行比较分析。

1 壳体失稳分析的原理及计算方法

一般求解失稳/屈曲问题的分析方法，是由ANSYS提供的两种预测结构屈曲临界载荷和屈服模态的技术，一种是特征值屈曲分析，另外一种是非线性屈曲分析。特征值屈曲分析用于预测一个理想弹性结构的理论屈曲强度(分叉点)。但初始缺陷和非线性使得很多实际结构都不是在去理论屈服强度处发生屈曲，因此特征值屈曲分析经常得出非保守结构，通常不能用于实际的工程分析。非线性屈曲分析比线性屈曲分析更精确，应用非线性技术，模型中就可以包括诸如初始缺陷、塑性、间隙、大变形响应等特征。此外，用户还可以跟踪结构的后屈曲行为［2］。

1.1 特征值屈曲分析的原理和计算方法

分析结构的稳定性时，在基于线弹性的特征值屈曲响应分析中，结构屈曲的临界载荷可表示为

式中 PQ为作用载荷;λi为屈曲特征值或屈曲载荷因子。

λi的计算方程为

式中 ［KL］为结构总体弹性刚度矩阵即小位移的线性刚度矩阵;［KG］为结构总体几何刚度矩阵，也称初始应力刚度矩阵;{δ}是特征位移向量。

线性屈曲有限元计算的实质就是计算整体结构在线性结构刚度基础上加上初始应力刚度影响后的结构屈曲的最小临界载荷。对于特征值λi得求解问题，ANSYS提供了Subspace(子空间法)和Block Lanczos(兰索斯分块法)两种求解方法。

1.2 非线性屈曲分析的原理和计算方法

非线性屈曲分析是一种逐渐增加载荷的非线性静力分析技术，求得使结构开始变得不稳定时的临界载荷。应用非线性技术，模型中就可包括诸如初始缺陷、塑性、间隙、大变形响应等特征。此外，使用偏离控制加载，用户还可跟踪结构的后屈曲行为。图1为一般的非线性载荷变形曲线，该图说明了理想载荷路径、有缺陷结构的载荷路径和该结构的实际动态响应。

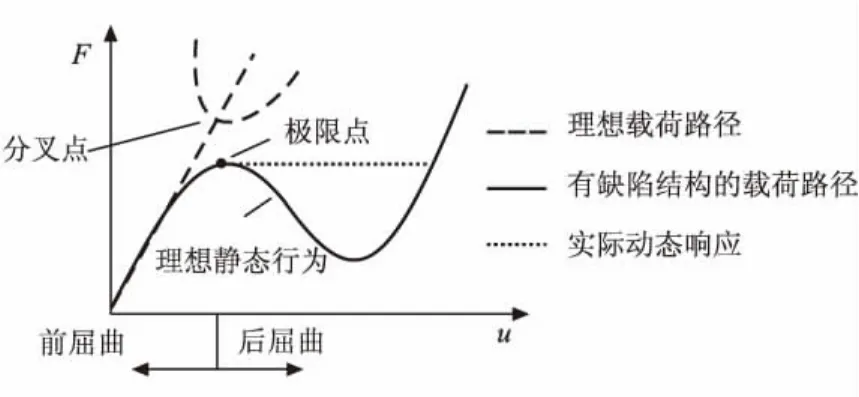
图1 屈曲载荷-位移曲线Fig.1 Curve of critical buckling load vs displacement

ANSYS程序通过使用牛顿-拉普森平衡迭代进行非线性求解，在某个容限范围内，它使每一个载荷增量的末端解都达到平衡收敛。在每次求解前，NR方法估算出残差矢量，这个矢量是回复力(对应于单元应力的载荷)和所加载荷的差值。之后，程序使用非平衡载荷进行线性求解，并核查收敛性。如果不满足收敛准则，则重新估算非平衡载荷，修改刚度矩阵，获得新解，持续这种迭代过程直到问题收敛。

对某些物理意义上不稳定系统的非线性静态分析，如果仅使用NR方法，正切刚度矩阵可能变为降秩矩阵，从而导致严重的收敛问题。对于这样的情况，可激活另外一种迭代方法——弧长方法，来帮助稳定求解。弧长方法使NR平衡迭代沿一段弧收敛，这样即使当正切刚度矩阵的值为零或负值时，也往往阻止发散。

图2为传统NR方法与弧长方法的比较。

图2 传统的NR方法与弧长法的比较Fig.2 Comparison of NR method and arc-length method

2 无加强环壳体外压失稳的有限元分析

2.1 有限元模型的建立

文中根据壳体的实际结构，建立了壳体前接头、前连接裙、前后堵盖以及壳体结构的实体模型。壳体材料为超高强度钢，弹性模量为210 MPa，泊松比为0.3。

模型可利用Pro/E建立，如图3(a)所示。之后，导入ANSYS中进行分析，计算主要使用solid185和shell181单元。

2.2 屈曲分析

对壳体有限元模型进行线性屈曲分析，得到其线性临界外压载荷0.164 MPa。一阶屈曲波形见图4。其中，图4(a)为无加强环壳体的整体屈曲波形图及屈曲波形剖视图。壳体外压一阶屈曲变形的母线变形半波数为1，环向变形波数为3。

图3 有/无加强环壳体有限元网格模型Fig.3 FEM model of shell with and without reinforcement ring

在线性屈曲计算的基础上，将线性屈曲一阶模态乘以0.001缺陷系数叠加到初始结构，使原结构有一定的初始几何缺陷，进行非线性屈曲计算。取壳体筒段表面径向位移最大值所在节点进行分析，其径向位移随载荷变化曲线见图5(a)，轴向位移随载荷变化曲线见图6(a)。在初始段位移随载荷呈线性增长，载荷达到一定值后，载荷小幅增长，位移大幅增长。以位移增幅最大的点为失稳点，得到壳体的临界载荷为0.160 MPa。

表1对无加强环壳体最大径向位移处节点失稳状态进行了描述，了解了壳体受外压作用下其受力、变形特性，得到了壳体在临界载荷作用下其径向位移为0.113 mm。

图4 壳体屈曲波形图Fig.4 Buckling mode of shell

图5 壳体载荷-径向位移曲线Fig.5 Curve of radial displacement vs load of shell

图6 壳体载荷-轴向位移曲线Fig.6 Curve of axial displacement vs load of shell

表1 无加强环壳体最大径向位移处节点失稳状态描述Table 1 Status description of the maximum radial displacement node on the shell without reinforcing ring

3 带加强环壳体外压失稳的有限元分析

为了加强壳体承受外压的能力，一般采用在壳体段增设加强环。有加强环的壳体在承受外压时，有2种失稳形式:第1种是加强环段内的壳体失稳破坏;第2种是壳体总体失稳破坏。两者的差别在于加强环的刚度是否满足稳定性要求:当加强环刚度足够时，壳体的失稳形式为第1种;当加强环刚度不足时，壳体的失稳形式为第2种。

为了分析加强环对壳体稳定性的影响情况，以及优化设计加强环，在加强环质量不变的情况下，对加强环以不同形式分布的壳体进行稳定性分析。加强环的总长度为200 mm，厚度为3.1 mm。

3.1 有限元模型建立

以壳体均匀分布2个加强环的情况为例，根据壳体实际结构采用Pro/E建立壳体的3维几何模型;之后，导入ANSYS中进行稳定性分析，壳体的有限元模型如图3(b)。其中，每个加强环的长度为100 mm，厚度为 3.1 mm。

3.2 屈曲分析

对图3(b)的壳体有限元模型进行线性屈曲分析，得到其线性临界外压载荷0.318 MPa。一阶屈曲波形见图4。其中，图4(b)为带加强环壳体的整体屈曲波形图及屈曲波形剖视图。壳体外压一阶屈曲变形的母线变形半波数为1，环向变形波数为3。

在线性屈曲计算的基础上，将线性屈曲一阶模态乘以0.001缺陷系数叠加到初始结构，使原结构有一定的初始几何缺陷，进行非线性屈曲计算。取壳体筒段表面径向位移最大值所在节点进行分析，其径向位移随载荷变化曲线见图5(b)，其轴向位移随载荷变化曲线见图6(b)。在初始段位移随载荷呈线性增长，载荷达到一定值后，载荷小幅增长，位移大幅增长。以位移增幅最大的点为失稳点，得到壳体的临界载荷为0.305 MPa［3-6］。带加强环壳体最大径向位移处节点失稳状态描述见表2。

表2 带加强环壳体最大径向位移处节点失稳状态描述Table 2 Status description of the maximum radial displacement node on the shell with reinforcing ring

3.3 计算结果的分析

之后，分别对不同加强环分布形式壳体进行外压稳定性分析，得到的结果见表3、表4和图7。为了方便分析有无加强环对壳体稳定性的影响，把无加强环壳体的计算结果也添加在其中。

表3 不同加强环分布形式壳体的临界失稳载荷比较Table 3 Critical buckling load of shell with different distribution of reinforcement ring

表4 不同加强环分布形式壳体最大径向位移处节点失稳状态比较Table 4 Status description of the maximum radial displacement node on the shell with different distribution of reinforcement ring

由表3可清楚看到，壳体的线性特征值屈曲解和几何非线性屈曲解的差别较小，都在5%以内，且加强环可有效地提高壳体的外压承受能力，均匀分布2个加强环的壳体，其临界屈曲载荷是无加强环壳体的1.93倍;均匀分布4个加强环的壳体，其临界屈曲载荷是无加强环壳体的3.63倍。表4则描述了不同加强环分布形式壳体在外压临界载荷作用下的变形、受力状态。

在不同加强环分布壳体一阶屈曲环向变形波数相同的情况下，其临界载荷相差不大。但在壳体一阶屈曲环向变形波数由3个变为2个之后，其临界载荷有大幅的提升。所以，均匀分布4个加强环的壳体为较优的选择，它的临界载荷较均匀分布2个加强环的壳体有明显提高，且其制造工艺相比，有5个加强环的壳体要容易。如果选择均匀分布4个加强环壳体，在满足壳体外压稳定性的前提下，可相应地减少加强环尺寸，减少加强环的材料，使壳体的重量减轻，达到轻型化的目的。

由表4、图7可知，壳体的主要变形为径向变形，其大概是轴向变形的百倍。不同的加强环分布形式对壳体的变形影响不大，同时壳体的应力、应变也变化不大。

图7 壳体载荷-径向/轴向位移曲线Fig.7 Curve of radial/axial displacement vs load

不同加强环分布形式壳体的载荷-位移曲线变化趋势一致:初始段载荷与位移呈线性变化，达到一定载荷后出现拐点，进入非线性段，载荷小幅增长，位移大幅增加。但拐点过后，不同加强环分布壳体的载荷-位移曲线高度明显不同，相同径向位移的条件下，均布4个大概是均布2个的2倍，均布2个大概是没有加强环的 2 倍［7-8］。

4 壳体外压试验

4.1 壳体外压试验情况

采用带2个加强环的壳体进行外压试验。试验前，壳体用前后堵盖密封以立式置于标准容器中，采用水介质进行加载。应变测点在壳体筒段的中心位置，压力测点在前堵盖位置。

外压加载为均匀加载，试件加载至压力显示为0.24 MPa时，压力显示明显降低。应变测点的应变值出现跳变。

从试验过程中压力的降低和应变值的跳变说明壳体已经失稳，此时的压力显现为0.24 MPa。由于采用水介质加载，所以壳体筒段中心的压力载荷为0.26 MPa，也就说明壳体的失稳载荷为 0.26 MPa。

4.2 试验和计算结果的比较分析

计算和试验结果比较见表5，壳体临界失稳载荷的计算结果和试验结果较吻合，试验结果大概是计算结果的87%。对于导致这个差异的原因，主要有以下方面:

(1)壳体结构中的初始缺陷及其对初始缺陷的敏感程度。作为影响壳体外压承载能力的一个重要因素，初始缺陷的设定无疑是一个重要的方面。文中采用一致缺陷模态法施加初始缺陷，尽管这可有效地模拟实际结构的初始缺陷，但毕竟和实际结构的初始缺陷有一定差距。

(2)壳体结构的几何非线性和材料非线性性能及其解法。文中考虑了结构的几何非线性，但由于结构的屈曲载荷距离使材料屈服还有一段距离，所以就没有考虑结构的材料非线性。

(3)壳体结构的边界条件。结构实际的边界约束与对边界约束的理论描述之间存在很大差异了;通常在理论上对边界约束的描述不是过于刚硬，就是过于柔软。

(4)壳体结构的连接方式以及载荷类型与分布。壳体结构实际受到的载荷有一定的载荷梯度，而在计算中采用了均布外压的方式加载，这就有可能造成计算结果和试验结果的差异。

表5 计算和试验结果比较Table 5 Test and calculate result

5 结论

(1)对无加强环壳体进行外压稳定性分析，了解了壳体在外压作用下的受力、变形特性，得到了其临界外压载荷为0.164 MPa，以及其在临界外压作用下产生的径向位移为0.113 mm。

(2)为了优化设计壳体加强环，在加强环总质量不变的情况下，对不同加强环分布形式壳体进行外压稳定性分析，分别得到其临界外压载荷，以及壳体在临界外压载荷作用下产生的变形。得出均布4个加强环壳体为较优选择，其临界载荷为0.591 MPa。

(3)对均布2个加强环壳体进行外压试验，其试验结果和计算结果较吻合。之后，也分析了造成误差产生的原因。

［1］余军昌，徐超，张峰，等.基于ANSYS的外压圆柱壳的屈曲分析［J］.轻工机械，2013(2):1005-2895.

［2］张宗尧，赵石军.基于ANSYS的外压容器稳定性分析［J］.设计与计算，2010(2):1673-3355.

［3］任萍，侯晓，何高让，等.外压载荷分布形式对固体火箭发动机结构稳定性的影响［J］.强度与环境，2011(2):1006-3919.

［4］任萍，侯晓，何高让，等.模拟壳体/燃烧室外压承载能力研究［J］.航天器环境工程，2011(2):1673-1379.

［5］梁力锦，陈冰冰，高增梁.外压圆筒临界压力的双非线性ANSYS有限元模拟与讨论［J］.设计计算，2013(1):1001-4837.

［6］尤军峰，陈汝训.固体火箭发动机后封头屈曲分析［J］.固体火箭技术，2008(2):1006-2793.

［7］Goy Der Hgd，Whi Ter G.Vibration power flow from machines into built-up structures［J］.Journal of Sound and Vibration，1980，68(1):59-117.

［8］Sun H L，Zhang K，Zhang P Q，et al.Application of dynamic vibration absorbers in floating raft system［J］.Applied Acoustics，2010，71(3):250-257.

(编辑:崔贤彬)

Buckling analysis on conical shell of solid rocket motor under external pressure

YU Wen-xue，XU Bing-heng，LIU Hong-chao，SHAN Lin
(The 41st Institute of the Fourth Academy of CASC，Xi′an 710025，China)

Stability of solid rocket motor′s conical shell under external pressure was investigated through buckling analysis and tests.The variation buckle load，mode，axial displacement and radial displacement curves with external pressure were obtained from buckling analysis of the shell.The buckling analysis on shell with reinforcement ring was also made.Calculated results reveal that reinforcement ring improves the stability of shell under external pressure.The buckling analysis in different distribution of reinforcement ring was also made.And the calculated results reveal that the shell with 4 reinforcement ring is a good choice when the length of reinforcement ring is a constant.Critical buckling load obtained from tests agrees well with the calculated results.

shell;external pressure;reinforcement ring;variation buckle load

V438

A

1006-2793(2014)04-0551-05

10.7673/j.issn.1006-2793.2014.04.023

2013-10-17;

2013-11-14。

余文学(1989—)，男，硕士生，研究方向为发动机外压稳定性。E-mail:729234089@qq.com