基于多因素模糊判决的多模型机动目标跟踪

刘扬, 闫新庆, 国强

(1.华北水利水电大学 信息工程系, 河南 郑州 450000；2. 哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

多模型估计在处理结构未定和参数变化问题上取得了极大成功，近年来受到人们越来越多的重视。传统的多模型估计中，需要预先设定一个有限模型集来逼近整个系统的模式空间，由于其具有固定的拓扑结构，因此通常被称为固定结构多模型方法(fixed structure multi-models method, FSMM)。然而，FSMM在应用中所预先设定好的模型集常无法完全覆盖整个系统模式空间，导致算法精度下降；而过多的模型又往往导致计算量的激增引起模型间不必要竞争。为克服FSMM的局限性，李晓榕提出变结构思想[1]，通过对量测及验前验后信息的融合，使模型集能够实时的自适应调整。多因素模糊综合评判为人们解决多因素、多变量的复杂问题提供了一种有效的思路和方法。可以根据实际需要，灵活构造模糊因素集、评价集、权集以及合成运算模型，以实现实时、快速、准确的在线决策。但截止到目前，该技术还没被用于模型的在线决策，本文引用多因素模糊综合判决思想，提出了一种基于多因素模糊综合评判的多模型方法(multi-factor fuzzy integrated evaluation,MFIE_MM)，把影响模型实时决策的多种因素综合考虑，简化模型集自适应策略(model set adapter, MSA)，力求更加快速准确的在全体模型集合中选出与当前系统真实模式最接近的变结构模型集合，并在其基础上实现对机动目标的快速准确跟踪。

1 变结构多模型方法基本思想

变结构多模型方法(variable structure multi-model method, VSMM)是对FSMM的一种改进，在任意时刻，它对系统状态的估计是在一个较少的、依赖于前一时刻系统模式的模型集合上进行的，而不是在系统整个可能模型集上[1-4]。VSMM和FSMM之间的主要区别体现在两次循环之间模型集的变化上。FSMM方法在仿真运行的整个过程中使用同一个模型集，而VSMM方法则根据目标机动的实际情况，利用MSA策略实时确定与系统真实模式较为接近，模型个数更加精简的模型集合。

一个VSMM估计器通常由模型集自适应策略(MSA)和模型集合序列条件估计(MSSCE)2个功能模块组成。MSSCE处理过程类似于FSMM算法，是VSMM方法的估计部分，能够基于确定的模型集合序列提供最好的可能估计，文献[5]侧重于对MSSCE的改进。而MSA策略能够利用包含在量测序列中的实时系统模式信息与包含系统模式的先验知识，实时确定当前时刻的有效模型集，是VSMM方法的技术核心。而VSMM方法性能的优劣也主要取决于MSA策略的好坏，同时MSA策略也是VSMM与传统FSMM的根本区别。

2 MFIE_MM中的MSA策略

模糊综合评价法是一种基于模糊数学的综合评标方法。该方法根据模糊数学的隶属度理论把定性评价转化为定量评价，由于其具有结果清晰，系统性强的特点在实际中得到广泛应用[5-11]。以多因素模糊综合评判技术为指导思想的MSA策略，其整体信息处理流程如图1所示。

首先，针对参与状态估计的各个模型，提取与状态估计密切相关的重要因素，建立相应的模糊多因素集，这些因素将在MSA 策略中作为模型选择的主要依据，同时因素数量要尽量精简，以保证算法的运行效率；在利用多因素模糊综合评判技术构建MSA策略时，除具备因素集U={u1,u2,…un}之外，还必须选择合适的评价集和单因素判决函数。如果把一个模型与当前时刻系统真实模式s的接近程度分为m个等级，则由分类结果构成的集合被称为评价集，记为V={v1,v2,…vm}。其中，vk表示第k个等级的评判结果。对任意一个模型在k时刻的评判结果实际上是V上的一个子集。 从U到V的模糊关系矩阵为R=(rkl)n×m，其中rkl表示考虑第k个因素时，模型集合中的元素与当前时刻系统真实模式s关联得到的第l种结果的可能程度，而R=(rkl,rk2,…,rkm)，k=1,2,…m表示仅仅从单因素uk考虑一个模型与系统真实模式s的接近程度，得到的单因素评判，因此，R被称为单因素评价矩阵。而一个模型与系统真实模式s相关的综合评价是因素权重模糊集A与单因素评价矩阵R的复合作用，亦即合成运算。由A与R的合成运算得到用于描述一个模型在k时刻准确度的模糊集B:

(1)

其中，“·”表示合成运算；bk表示一个模型对于第k个评价等级vk的隶属度。

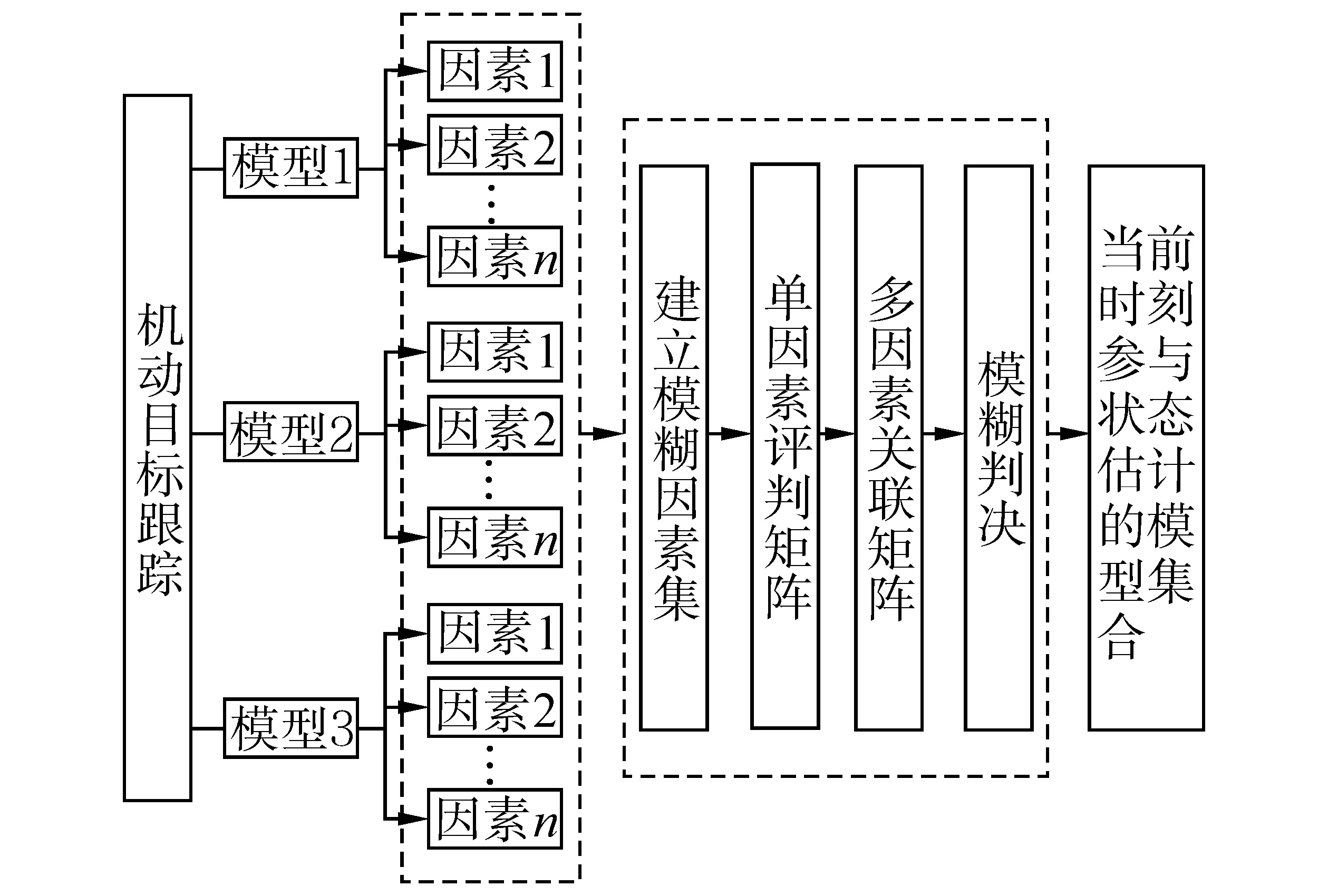
图1 MFIE_MM中的MSA策略

3 MFIE_MM设计与实现

3.1 模糊因素集的确定

(2)

3.2 模糊评判集的确定

在模型评判过程中，仅仅对一个模型mi在当前时刻是否与系统真实模式s逼近感兴趣。因此从实际问题出发，选择评价集V={v1,v2,…vm}中的等级数m=2，其中，v1表示准确；v2表示不准确。即V={准确,不准确}。而对于模糊隶属度函数的确定，这里选择正态隶属度函数，基于第k个因素判决一个模型是否准确的隶属度计算公式为：

(3)

当按照模型中某一个因素评判时，应该有rk1+rk2=1，即

(4)

因此，模糊评判矩阵为R=(rls)n×2

3.3 计算多因素模糊评判矩阵与相似度

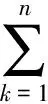
(5)

为了更好的研究机动目标跟踪过程中，各个模型i与系统真实模式s间的相似性，定义模型i与系统真实模式s之间的紧密度gij(k)：

(6)

式中：gij(k)的值域为[0,1],如果gij(k) 趋于1，则在k时刻，模型与系统真实模式s的相似度较高，即模型的准确度较高；如果gij(k) 趋于0，则模型i与系统真实模式s的相似度较低，即模型的准确度较低。在MSA策略实时选择最优模型集合的过程中，当利用多因素综合判定方法选出最佳模型后，利用概率转移矩阵激活与最佳模型相毗邻的模型[4]，得到下一时刻参与状态估计的模型集合，并利用先验信息将新的模型集合进行初始化。

3.4 算法流程

经过上述对MSA策略的设计后，MFIE_MM的流程图如图2所示。

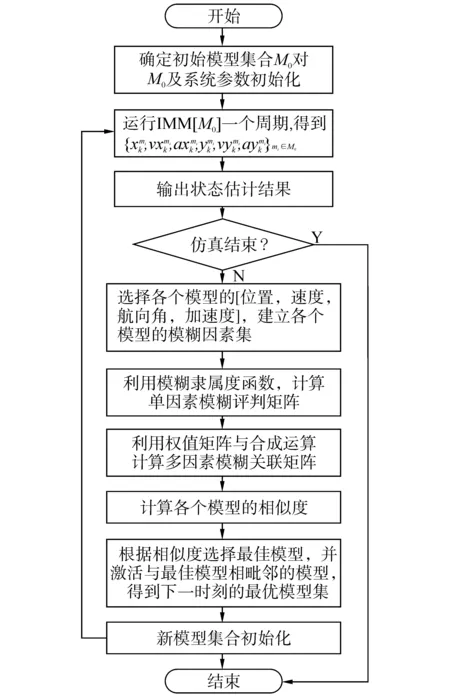
图2 MFIE_MM流程图

仿真运行开始，首先对模型集合M0进行初始化，并针对模型集合M0运行IMM[M0]一个周期计算各个状态估计向量的加权和；然后计算当前时刻各个模型mi与系统真实模式s的相似度，并选择“准确度最高”的模型作为下一时刻模型集合的中心；最后利用实时的量测信息与先验知识对新模型集合进行重初始化，为进入下一个IMM[Mk+1,Mk+1]循环做好准备。

4 机动目标跟踪中的MFIE_MM

4.1 仿真场景设计

本文假设机动目标的加速度变量通过将加速度空间A量化得到，如式(7)所示，加速度之间的跳变由马尔科夫概率转移矩阵决定：

(7)

传统FSMM在整个算法运行过程中，所使用的模型集如图3所示，同时，图3也是MFIE_MM的模型全集，某一时刻MFIE_MM所使用的模型集合是图3中模型集合的子集。图4(a)中黑色标注模型表示MFIE_MM在仿真开始时刻所使用的模型集M0={m1,m2,m3}；图4(b)表示运行MFIE_MM一个周期后，当前时刻MFIE_MM所使用的模型集合Mk={m3,m5,m7}。

图3 FSMM方法中的模型集

(a) MFIE_MM仿真开始时所使用的模型集

(b) MFIE_MM时刻1所使用的模型集

为了验证算法性能，用蒙特卡洛方法进行50次仿真，仿真中采样周期T=0.02 s，仿真时间20 s，因此仿真拍数为1 000拍，目标状态向量初始化为：

(8)

方程中的状态转移矩阵Φ、量测矩阵H和过程噪声分布矩阵G分别为

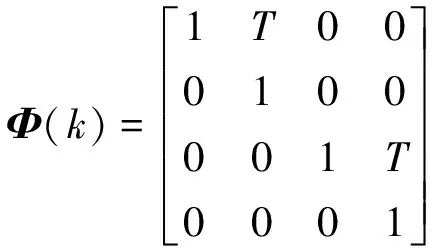
(9)

(10)

(11)

过程噪声方差Qx=0.001,测量噪声方差Rx=0.5 m，传统FSMM模型集合初始化为MFSMM={m1,…,m7}，模型概率初始化为：m1=…=m7=1/7。MFIE_MM模型集合初始化为MMFIE_MM={m1,m2,m3}，模型初始概率：m1=m2=m3=1/3。取模糊因素集为U={u1,…,u4}，各因素的计算如下：

(12)

(13)

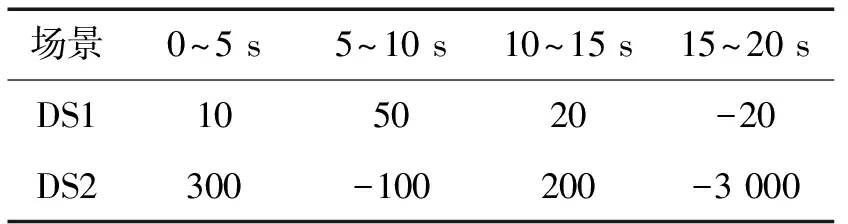
表1 仿真场景设计x轴方向加速度

为更好地检验算法性能，本文选择对比算法为传统FSMM和期望模式扩充 (EMA)变结构多模型方法[2,6]，并设计2种仿真场景，如表1所示，表中第1、2行数值表示不同时间段下目标在x轴方向上的加速度值ax。其中，DS1、DS2分别设计为弱机动和强机动仿真环境，在上述环境下分别运行3个目标跟踪算法。并统计各个算法的误差均值、误差协方差、单拍运行时间、模型平均误差和所利用平均模型个数。

4.2 仿真结果与分析

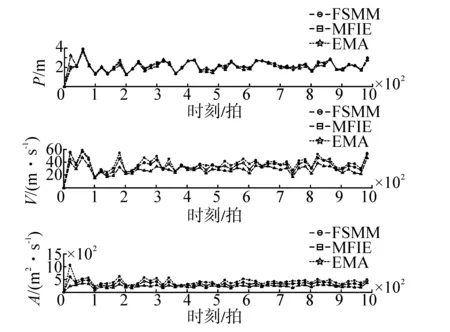
图5表示DS2下FSMM、EMA、MFIE_MM3种方法对位置、速度变量的估计结果，x轴方向表示仿真时间。图6(a)表示在强机动场景DS2下，FSMM、EMA、MFIE_MM这3种方法在位置、速度和加速度变量上的误差标准差。图6(b)显示在场景DS2下，FSMM、EMA、MFIE_MM在整个仿真过程中，所用模型集合的平均误差，这里的平均误差用各个模型的加速度参数来描述。

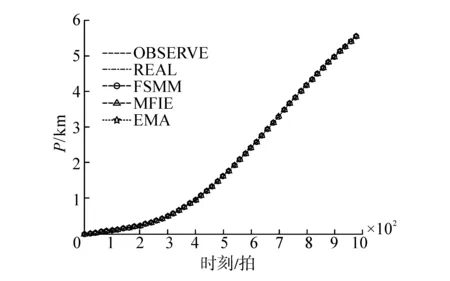
图7表示在弱机动场景DS1下，FSMM、EMA、MFIE_MM这3种方法分别对位置、速度变量的状态估计结果。

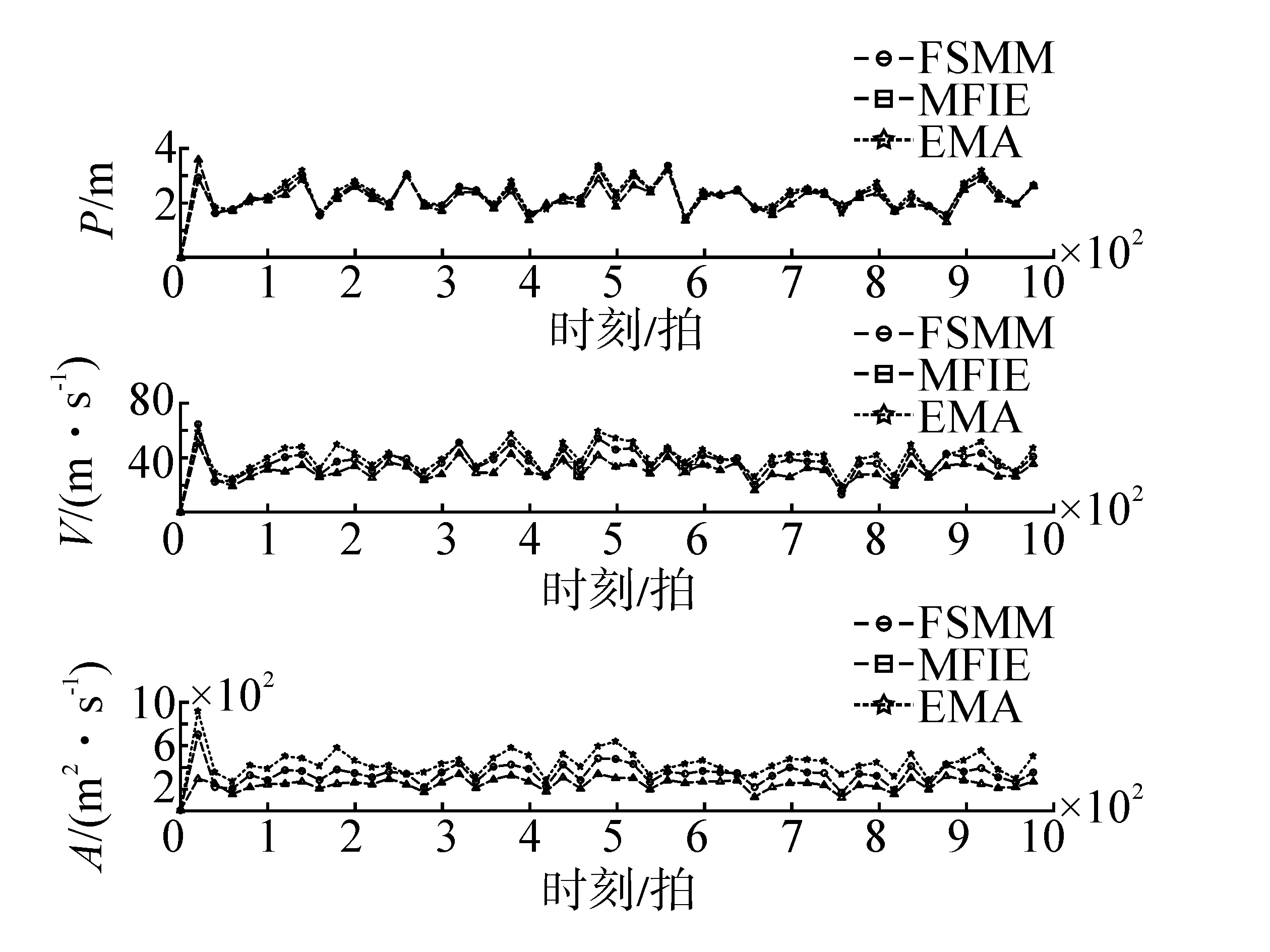
图8表示在弱机动场景DS1下，FSMM、EMA、MFIE_MM这3种方法的状态估计。

(a)位置变量估计结果

(b) 速度变量估计结果

(a)估计误差标准差

(b) 模型误差均值

(a)位置变量估计结果

(b) 速度变量估计结果

(a)估计误差标准差

(b) 模型误差均值

表2、表3分别统计了FSMM、EMA与MFIE_MM在强、弱机动场景下，对位置、速度、加速度变量的估计误差标准差。从图5～图7的显示结果以及表2，表3的数据统计结果可以看出，无论对弱机动场景还是强机动环境，MFIE_MM方法对位置、速度、加速度参数估计的精度都明显优于传统的FSMM和EMA。从图6(b)、图8(b)中可以清楚的看到MFIE_MM方法无论在强机动环境还是弱机动环境，所使用模型集合的平均误差明显低于FSMM和EMA所使用的模型集合，这就说明MFIE_MM方法所利用的MSA策略在模型集合的实时确定过程中，能够有效的选择与系统真实模式s较为接近的模型集合，从而显著提高算法估计精度。由表3通过对3种多模型方法参数估计误差均值的统计可以看出，相比于FSMM、EMA方法，MFIE_MM的误差均值最小，尤其是在仿真开始阶段，MFIE_MM误差明显优于传统FSMM方法和已有的EMA变结构多模型方法，也就是说MFIE_MM方法在有效提高参数估计精度的同时，算法的稳定性也有所改善。

表4统计了FSMM、EMA、MFIE_MM在不同场景下的性能参数，统计内容包括：处理单拍数据耗费的时间均值；仿真运行过程中各个方法所利用模型个数的均值，由统计结果表明，在算法运行过程中，MFIE_MM所使用的模型平均个数为2.997个，FSMM使用6.993个，EMA使用7.964个，说明MFIE_MM方法在使用较少模型个数的基础上也实现了对目标的有效跟踪。同时，MFIE_MM单拍运行时间几乎只有FSMM方法的一半，分析其原因，一方面源于MFIE_MM简单有效的模型选择逻辑，即优秀的MSA策略；另一方面源于MFIE_MM在处理过程中所利用的精简的模型个数。

表2 DS1和DS2下的估计误差标准差比较

表3 DS1和DS2下的估计误差均值比较

表4 DS1和DS2下的算法性能参数比较

5 结束语

本文在变结构多模型方法的思想上，引入多因素模糊综合评判技术，构造了一个实现逻辑简单，模型在线选择准确率较高的变结构多模型方法—MFIE_MM。MFIE_MM通过对模型全集中的各个成员建立模糊因素集，确定多因素模糊综合鉴别函数，得到各个模型的相似度，并根据相似度选择最佳模型，以实时生成参与状态估计的模型集合。仿真结果分析表明，不管在弱机动还是强机动环境下，MFIE_MM对各个参数的估计精度和算法稳定性都明显优于FSMM和EMA方法；同时，MFIE_MM由于其实现逻辑的简洁而具有FSMM和EMA方法无法比拟的运行效率。

参考文献：

[1]LI Xiaorong, BAR-SHALOM Y. Multiple-model estimation with variable structure, part I[J]. IEEE Transactions on Automatic Control, 1996, 41(4): 478-493.

[2]LI Xiaorong, ZHI Xiaorong, ZHANG Youmin. Multiple-model estimation with variable structure, part III: model-group switching algorithm [J]. IEEE Transactions on Aerospace and Electronic Systems,1999,35 (1): 225-241．

[3]LI Xiaorong, ZHANG Youmin. Multiple-model estimation with variable structure, part V: likely-model set algorithm [J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(2): 448-466.

[4]LI Xiaorong, JILKOV V P, RU Jifeng. Multiple-model estimation with variable structure, part VI: Expected-mode augmenta- tion[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(3): 853-867.

[5]林长川, 孙腾达. 雷达与AIS目标航迹模糊算法与仿真[J]. 系统仿真学报, 2006, 18(2): 903-907.

LIN Changchuan, SUN Tengda. Algorithm and simulation of fuzzy correlation of tracks from radar and AIS[J]. Journal of System Simulation, 2006, 18(2): 903-907.

[6]胡娟.油田开发规划模糊优化模型及其应用研究[D]. 成都：西南石油大学, 2013:1-142.

HU Juan. Fuzzy optimization model of oilfield development program and its application [D]. Chengdu:Southwest Petroleum University, 2013:1-142.

[7]段海滨,马冠军,赵振宇. 基于模糊规则和动态蚁群-贝叶斯网络的无人作战飞机态势评估[J].智能系统学报，2013,8(2):119-127.

DUAN Haibin, MA Guanjun, ZHAO Zhenyu. UCAV situation assessment based on fuzzy rules and dynamic ant colony-Bayesian network [J]. CAAI Transactions on Intelligent Systems,2013,8(2):119-127.

[8]李永新，陈增强，孙青林.基于模糊控制与预测控制切换的翼伞系统航迹跟踪控制[J].智能系统学报,2012,7(6 ):481-488.

LI Yongxin, CHEN Zengqiang, SUN Qinglin. Flight path tracking of a parafoil system based on the switching between fuzzy control and predictive control[J]. CAAI Transactions on Intelligent Systems, 2012,7(6 ):481-488.

[9]郝庆波.数控机床可靠性及维修性的模糊综合分配与预计[D]. 长春：吉林大学, 2012:1-147.

HAO Qingbo. Fuzzy comprehensive allocation and prediction for NC machine tools reliability and maintainability[D].Changchun: Jilin University China, 2012:1-147.

[10]刘三阳,杜喆. 一种改进的模糊支持向量机算法[J]. 智能系统学报,2007,2(3):30-33.

LIU Sanyang,DU Zhe. An improved fuzzy support vector machine method [J]. CAAI Transactions on Intelligent Systems, 2007,2(3):30-33.

[11]徐立中,林志贵,黄凤辰. 基于模糊证据理论的水质环境状态估计[J]. 智能系统学报,2007,2(3):79-83.

XU Lizhong, LIN Zhigui, Huang Fengchen. Water environmental qual ity assessment based on fuzzy evidence theory [J]. CAAI Transactions on Intelligent Systems , 2007,2(3):79-83.