舰载机阻拦过程动力学仿真

张智, 闻子侠, 朱齐丹, 张雯, 喻勇涛

(哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001)

舰载机阻拦过程是一个很复杂的物理运动过程，阻拦系统包括主液压缸、滑轮缓冲系统、末端缓冲系统等多个部分，并由阻拦钢索系统在各个液压滑轮间穿绕而成，阻拦过程钢索会产生复杂的波动和应力传递，并带动各个液压缓冲系统和滑轮组系统综合运动，形成复杂的综合运动规律，飞机阻拦过程还可能会出现不同偏心距、偏航角、俯仰和横滚姿态等变化，且飞机尾钩具有两个摆动自由度，挂索过程中飞机尾钩、飞机机体、和阻拦索之间也将产生复杂的运动制约关系。一些学者[1-4]采用力学分析、波动计算等方法分析阻拦过程阻拦索及飞机的受力状态，但仅能研究宏观规律或定性分析，难以细致、准确地反应阻拦过程中各种复杂规律。一些学者建立了阻拦过程仿真系统[5-6]，但大多对飞机、尾钩、阻拦索等一些环节作了较大简化，文献[7-11]侧重阻拦过程液压系统特性研究，建立了液压运动模型。但对阻拦过程飞机运动及阻拦索波动进行了忽略或简化。一些学者[12]采用LS-DYNA和ADAMAS等方法建立阻拦索系统的有限元计算模型，较为完整地反映了阻拦索、滑轮组系统和阻拦液压系统的运动规律，但飞机、阻拦钩模型仍较简化，难以准确反映阻拦过程飞机、阻拦钩和阻拦索之间复杂的运动规律。本文采用动力学仿真和阻拦索的有限元仿真方法结合，不仅建立了飞机、阻拦钩的完整动力学模型，且对阻拦索波动、阻拦系统滑轮组和液压系统的运动过程进行了详细建模。

1 舰载机及尾钩动力学建模

1.1 机体及起落架模型

考虑到着舰时刻飞机与航母的任意相对姿态，文献[8]中已建立完整六自由度机体及起落架模型，该模型可适应任意的飞机着舰过程，并且能实现倾斜姿态冲击地面时，机体和3个起落架支柱的联合动力学仿真，并实现了整个冲击过程的翻滚和颠簸过程模拟。本文只给出机体坐标系的定义形式。

飞机的3个欧拉姿态角定义为：偏航角ψP为纵轴xb在水平面xgyg上的投影与轴xg间的夹角；俯仰角θP为纵轴xb与水平面xgyg之间的夹角；滚转角φP为飞机对称平面xbzb与通过纵轴xb的垂直平面之间的夹角。可求Sb到Sg姿态变换阵：

(1)

式中：Lx(φp)为绕x轴旋转φp角度，Ly(θp)为绕x轴旋转φp角度，Lz(ψp)为绕x轴旋转φp角度。

1.2 尾钩动力学模型

1.2.1 尾钩坐标系定义

定义尾钩坐标系，OxTyTzT(标记为ST)，尾钩坐标系是以飞机坐标系为基准来定义的(即当尾钩3个姿态角均为0时，其坐标系与机体坐标系各轴平行)，坐标系原点定义在尾钩的旋转中心点。

尾钩的3个欧拉姿态角采用与飞机相同的定义形式(只是以飞机本体坐标系为基准)，分别为：偏航角ψT、俯仰角θT和滚转角φT。可求ST到Sb姿态变换阵：

(2)

从而可求ST到Sg变换阵

(3)

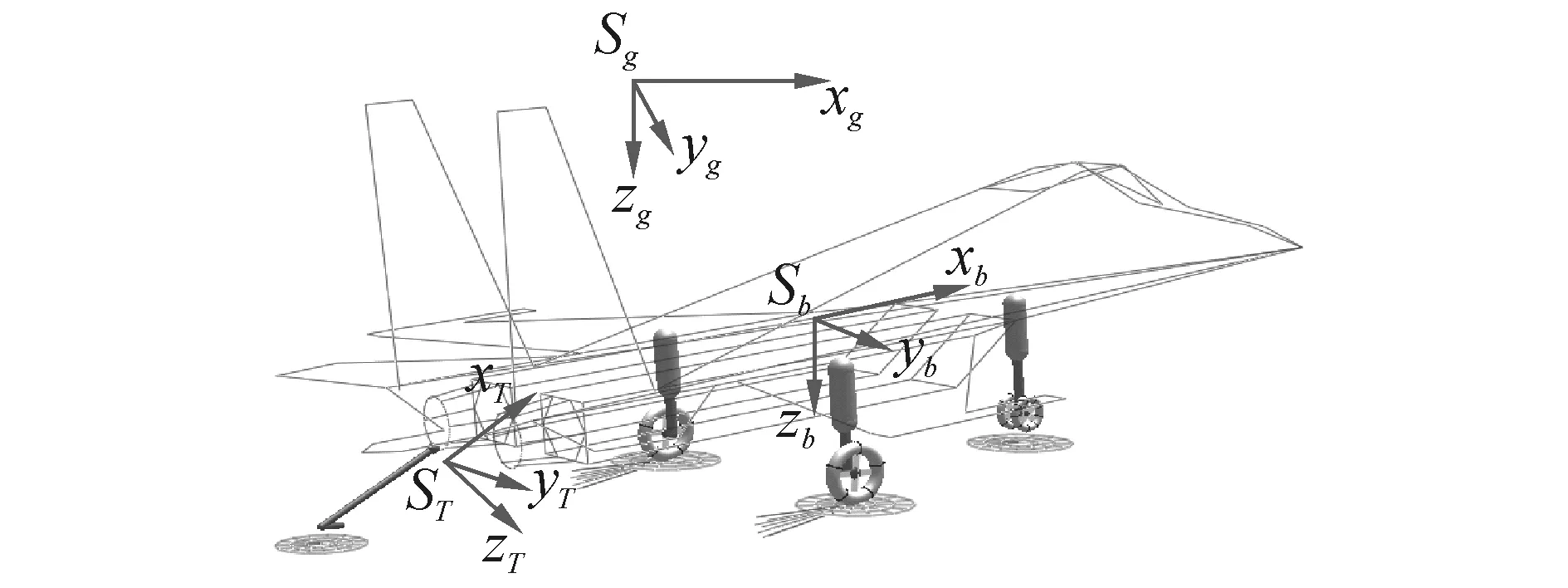
图1 尾钩坐标系

1.2.2 尾钩动力学方程

尾钩的坐标原点选在其旋转中心，与机尾固连，挂索过程机尾速度变化较小，故按惯性系处理。尾钩质量远小于飞机，其原点平动可视为与机尾固连，平动动力学不需计算，只需根据机体动力学模型中求得的飞机位置姿态直接推算其中心点的位置即可，设尾钩旋转中心点在飞机本体坐标系中的坐标PT_b=[xT_byT_bzT_b]T，则其在世界坐标系坐标Sg中的坐标PT_g=[xT_gyT_gzT_g]T可用下式求解:

(4)

式中：PP_b=[xP_byP_bzP_b]T为飞机质心在世界坐标系中的坐标，将式(1)代入式(4)后可求得PT_g。

尾钩旋转动力学及运动学方程如下：

(5)

式中：ωxT、ωyT、ωzT表示尾钩在其本体系ST中的3个角速度分量;IxT、IyT、IzT是尾钩在ST中的惯性矩，IzxT是飞机在ST中的惯性矩的惯性积；∑MT为合外力矩向量在尾钩本体系的表示。

1.2.3 尾钩受力计算

如图2，舰载机着舰过程中，尾钩到自身重力FT.G、地面弹力FT.gnd、纵向阻尼力FδTZ和横向阻尼力FδTH作用，因平动为受限运动，仅计算其旋转动力学模型，故需计算各个力产生的力矩。

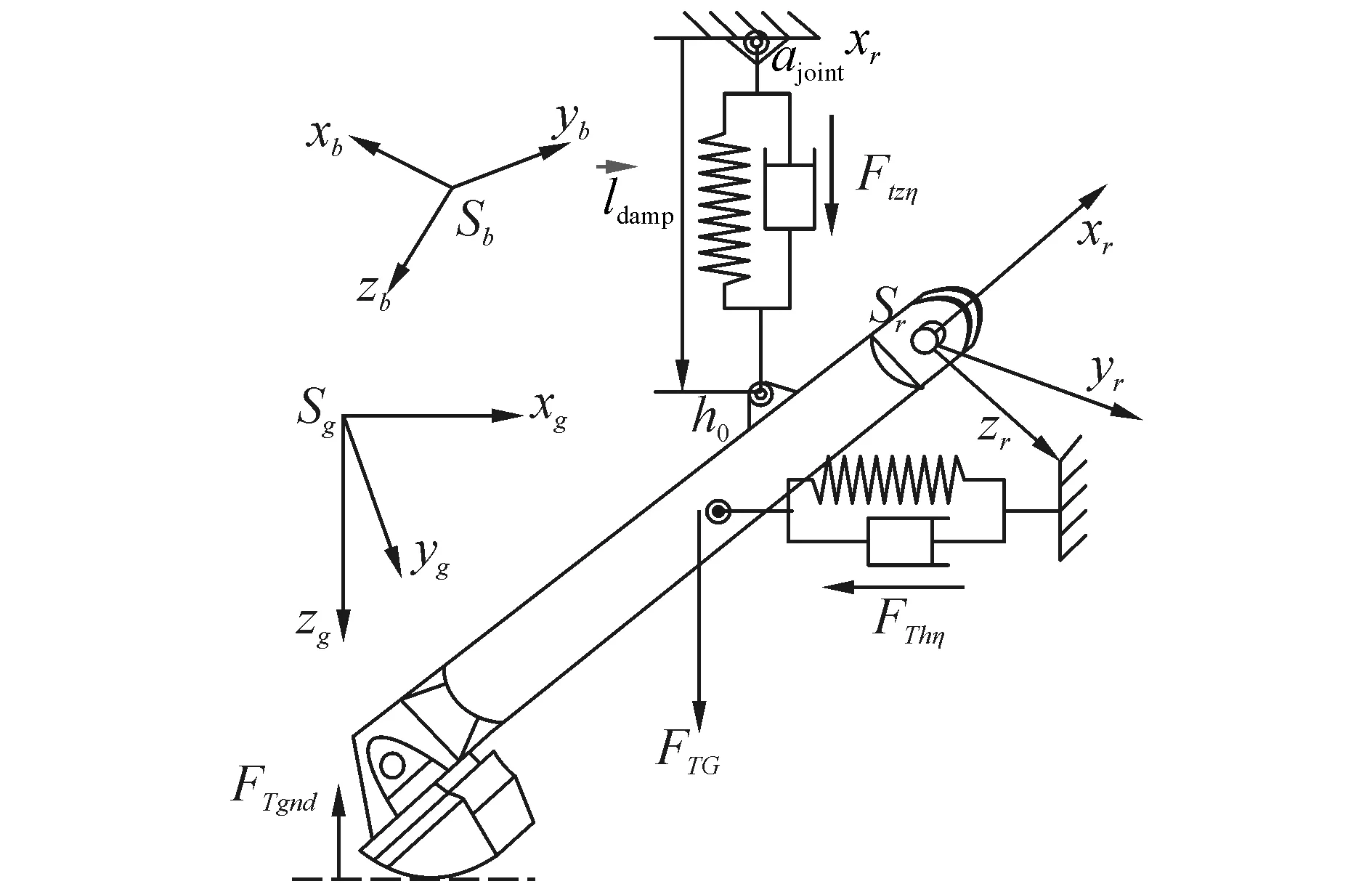
图2 尾钩受力分析

为适应式(5)动力学模型，需推导各力矩在尾钩坐标系中的表示。下面分别推导各个力和力矩的计算过程：尾钩坐标系下自身重力FT.G_G计算：

(6)

式中：LTg为式(3)给出的坐标变换阵的逆阵。则尾钩坐标系重力产生力矩MT.G_T=FZ.T.G_TlT.GE，FZ.T.G_T为FZ.T.G的尾钩系Z轴分量，LT.GO为尾钩重心距铰接点的距离。

尾钩坐标系下地面弹力FT.gnd_T计算：尾钩承受地面弹力FT.gnd_T是一个瞬间碰撞力，为便于与其他受力一起计算合力、并实现尾钩在整个阻拦过程的综合仿真，将碰撞受力过程简化为一个大刚度弹簧力加阻尼力的作用过程，即允许尾钩有垂向微小形变δT.h。设尾钩末端触地点在尾钩本体系的坐标为PT.e_T=[xT_eyT_ezT_e]T，那么其在大地坐标系坐标为：

(7)

则可求得尾钩垂向形变δT.h：

(8)

式中：zgnd为地面高度。从而计算尾钩的地面弹力大小计算公式如下：

(9)

从而计算尾钩坐标系下地面弹力矢量如下：

(10)

式中：kδ_T.gnd和kη_T.gnd分别为尾钩与地面碰撞的等效弹性系数和阻尼系数。

尾钩坐标系地面弹力产生力矩MT.gnd_T=FZ.T.gnd_TlT，其中FZ.T.gnd_T为FT.gnd_T的尾钩系z轴分量，lT为尾钩全长。

阻尼力计算：尾钩的阻尼力分为纵向阻尼力和横向阻尼力，用来限制尾钩着陆后的弹跳幅度，纵向阻尼力大小fT.ηz可由下式计算：

(11)

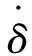
(12)

计算方法与纵向阻尼力类似，计算出阻尼力后，需乘以各自得阻尼力臂(与阻尼器安装位置有关)来求得阻尼力矩。

1.2.4 尾钩对飞机作用力计算

尾钩对飞机的作用力包括2部分:一部分是通过旋转铰接点对飞机传递的力，此处仅可传递拉力或支撑力，且沿着尾钩轴向；另一部分是横、纵向阻尼器连接在飞机上的固定点对飞机传递的阻尼反作用力。对于铰接点作用力，可先将尾钩受到的所有合外力变换至尾钩本体坐标系，并将变换后的y和z方向分量置0，仅保留x方向分量，然后再将该分力变换至飞机本体坐标系或世界坐标系，并施加于飞机机体动力学计算模型即可。

2 阻拦系统建模

2.1 阻拦系统简介

阻拦系统结构复杂[9]，阻拦索从甲板上向下穿绕，经过多个连接变向滑轮，首先经过左右滑轮缓冲系统(左、右滑缓)，然后分别从左右两侧进入主液压缸缓冲系统(主缓冲系统)的连接滑轮，分别在内外滑轮上各自缠绕9圈后，连接至左右末端缓冲系统(左、右末缓)，真实阻拦过程中，力在钢索中不可能是均匀分布，而是包含应力波动、弯折波动、钢索与滑轮的碰撞、摩擦等各种耦合作用，导致钢索中的力变化规律非常复杂，为真实体现索的受力及波动过程，本文引入有限元方法对钢索进行建模，同时对索的微元与滑轮、阻拦索接头、末端缓冲等部分的连接受力关系进行了建模。

2.2 阻拦索及接头建模

图3为本文采用的阻拦系统中的阻拦索和接头的模型简化示意，阻拦索考虑为弹簧质量球系统，接头考虑为六自由度运动的均匀圆柱体，仿真过程中所有的质量球运动状态采用三自由度动力学方程计算(忽略旋转自由度)，2个接头采用六自由度动力学方程计算。图中给出了阻拦索及接头初状态时与大地坐标系的相对位置关系。

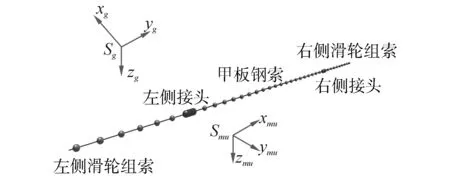
图3 阻拦索和接头仿真模型

2.2.1 阻拦索及接头建模

系统将绳索假设为均匀分布的质量球，以及连接球的弹簧，假设各球质量集中于一点，忽略球的半径及弹簧的质量等参数。这样每个球在收到左右两端弹簧力及外力的综合作用下，进行三维空间的动力学运动，将所有球的运动状态组合起来，就代表了索的波动及各段受力状态。

如图4，针对每个质量球i，设质量为Mbi，其左右两端分别连接着2个弹簧，弹簧另一端连接着Mbi-1和Mbi+1，那么该质量球同时受到左右弹簧的力FHl.i和FHr.i，及重力Gi的作用，则该球合外力为(式中各个力均为三维力矢量)：

(13)

质量球在大地坐标系的动力学及运动学方程描述如下：

(14)

(15)

式中：[Vx.mbiVy.mbiVz.mbi]T和[xmbiymbizmbi]T分别为该质量球在大地坐标系中的位置和速度，质量球只考虑其平动，不考虑转动，故不需列写转动方程。

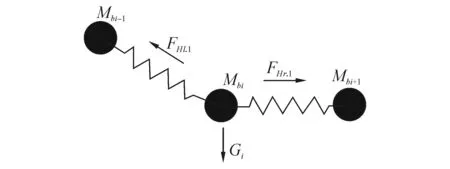
图4 质量球单元受力示意图

下面考虑弹簧力的求解。以左弹簧为例，设弹簧初始长度为l0，拉伸(压缩)后的当前长度为l，则弹簧弹力为：

(16)

式中：Kδ为刚索的弹性模量，拉伸后长度l由下式计算：

(17)

弹簧除受到弹力外，还受到拉伸速度带来的磨擦阻尼力，设连接弹簧两端的质量球运动速度分别为Vmb.i和Vmb.i-1，则弹簧的拉伸速度为

(18)

则该弹簧受到的摩擦阻尼力为

(19)

从而求得弹簧所受合力：

(20)

同理利用式(20)可求出右端弹簧受力FHr.i，分别代入式(13)，即可求得每个质量球的合外力，再由式(14)、(15)质量球动力学方程计算每个质量球的实时状态，即可完成整个阻拦索的仿真计算。

2.2.2 接头的六自由度动力学模型

如图3，接头考虑为均匀圆柱体，与其固连的本体坐标系为Oxmuymuzmu(标记为Smu)，原点定义在圆柱体中心，xmu轴与圆柱体的轴线重合，ymu轴在水平平面内并垂直于xmu轴，zmu轴垂直于Oxmuymu平面并指向下。与1.1节中机体定义相同，接头的3个欧拉姿态角定义为：偏航角ψmu、俯仰角θmu、滚转角φmu，从图3可以看出初始状态下接头与世界坐标系Sg相对位置关系，此时接头的偏航角ψmu=90°，其余2个角度均为0°。同理可求取接头坐标系到世界坐标系的变换矩阵：

(21)

接头的平动动力学方程与索的质量球动力学方程一致，设接头受到的瞬时合外力为FT(下节中求取)，速度和位置矢量分别为[Vx.muVy.muVz.mu]T和[xmuymuzmu]T，那么只要将以上变量分别替换式(14)和式(15)中相应项即可，此处不再列写。

接头的旋转动力学方程与尾钩旋转动力学方程一致，设其在本体系Smu中的角速度为[ωxmuωymuωzmu]T，Ixmu、Iymu、Izmu是接头在Smu中的惯性矩，Izxmu为是接头在Smu坐标系中的惯性矩的惯性积，∑Mmu为合力矩向量在接头本体系的表示。结合上文定义的接头欧拉角，采用式(5)的计算方程，并替换相应参量，即可得到接头的旋转动力学方程，此处不再列写。

2.2.3 接头与索模型的联立仿真

如图5，接头圆柱体两端分别通过弹簧与相邻的质量球相连，只要计算出左右弹簧拉力，并结合接头动力学模型和左右连接球的动力学模型，即可实现钢索与接头的联动仿真。

欲计算左右弹簧力，需计算其各自拉伸(压缩)位移及两端的拉伸(压缩)速度，其中左右连接的质量球的位置与速度已经计算，故在此仅需计算世界坐标系中接头左右两端的位置及速度。

设接头等效圆柱体长度为lmu，则接头左右两端点在其本体坐标系下的坐标分别为[-lmu/2 0 0]T和[lmu/2 0 0]T，从而可求得端点在世界坐标系下的坐标为：

(22)

将式(22)代入式(21)后即可求得接头端点的世界系坐标，继续计算接头两端的世界坐标系速度：

(23)

式中：ωmu_g为接头在世界坐标系中角速度矢量，根据以上计算结果，计算连接接头左右两端弹簧的拉力。以接头左端为例，设其连接的质量球为Mbi，对于接头连接的等效弹簧，其拉伸后长度为：

(24)

当前拉伸速度为：

(25)

当前弹簧拉伸长度为：

(26)

式中：l0为弹簧无伸长状态下的长度。式(25)和(26)已计算出连接接头处的等效弹簧的变形量及变化速度，参照式(16)和(19)的方法，即可计算弹簧的弹力FHl.N和速度摩擦力FHl.μ，从而求得弹簧合力。

图5 阻拦索和接头连接作用力计算

图6 接头与索的联合动力学仿真结果

弹簧合力一端作用于2.2.2节的接头的六自由度动力学模型，另一端作用于2.2.1节索的质量球动力学方程，便实现了索和接头的联合动力学仿真，接头右侧弹簧受力计算方法与左侧相同。对阻拦索及接头仿真模型施加一个虚拟的牵引力，其动态波动过程仿真结果如图6所示。

2.3 阻拦系统建模

2.3.1 阻拦索与滑轮作用模型

如图7，滑轮采用一个等效圆盘模型来计算，对所有与圆盘位置发生干涉的质量球，均受到圆盘的弹力、摩擦力和纵向约束力的作用，在此可令式(29)中δL_mbi的计算是否大于0作为干涉判定条件。阻拦系统中包含多个滑轮，但其摆放姿态可分为3种，分别平行于XY平面、YZ平面或XZ平面，无论是哪一种摆放姿态，均可通过在其摆放平面内计算与索的作用力来简化计算。下面以XY平面滑轮为例，推导其与钢索质量球的作用力，其他平面依此类推。

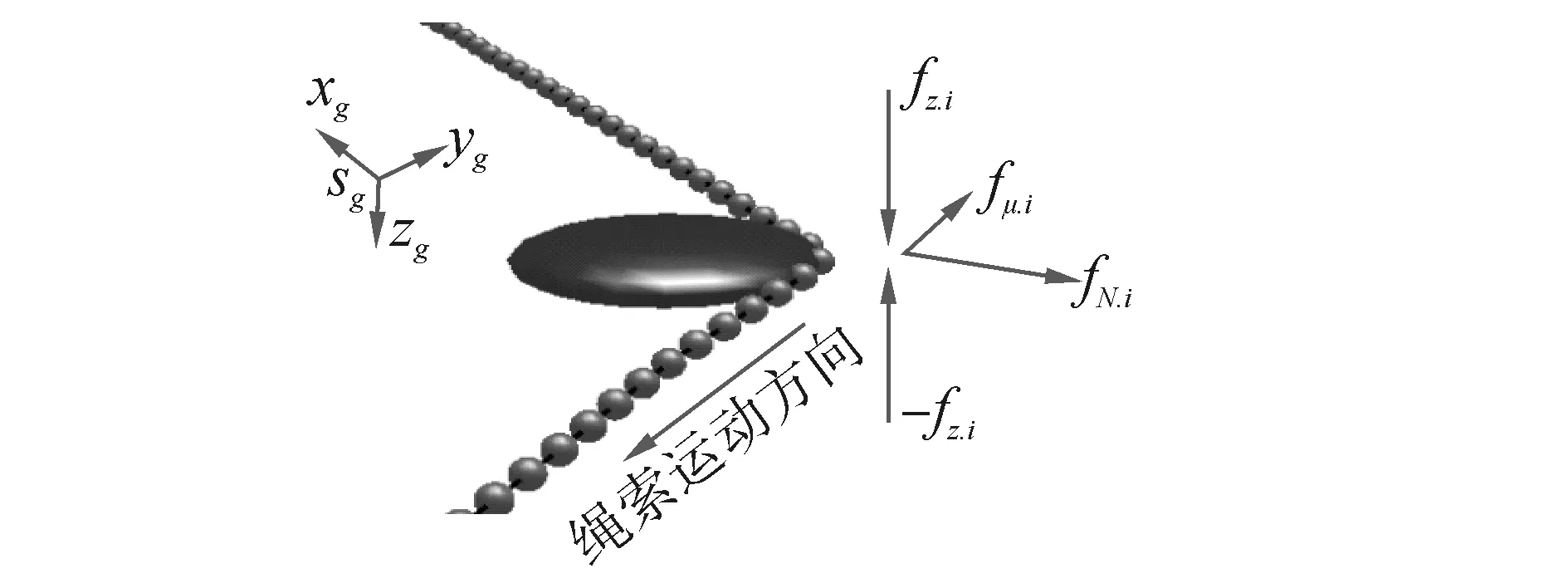
图7 阻拦索与滑轮作用模型

以质量球Mbi为例，设其在世界坐标系中的位置及速度矢量分别为[xmbiymbizmbi]T和[Vx.mbiVy.mbiVz.mbi]T，并设滑轮的中心坐标为[xLyLzL]T，质心在世界坐标系运动速度为[VxLVyLVzL]T，其半径为RL。

如图8，计算质量球位置与滑轮中心相对位置向量在世界坐标系XY平面中的象限角θL_mbi为：

(27)

式中：atan2为广义反正切函数，可根据横纵坐标的相对位置关系，求取其在360°范围内的象限角。

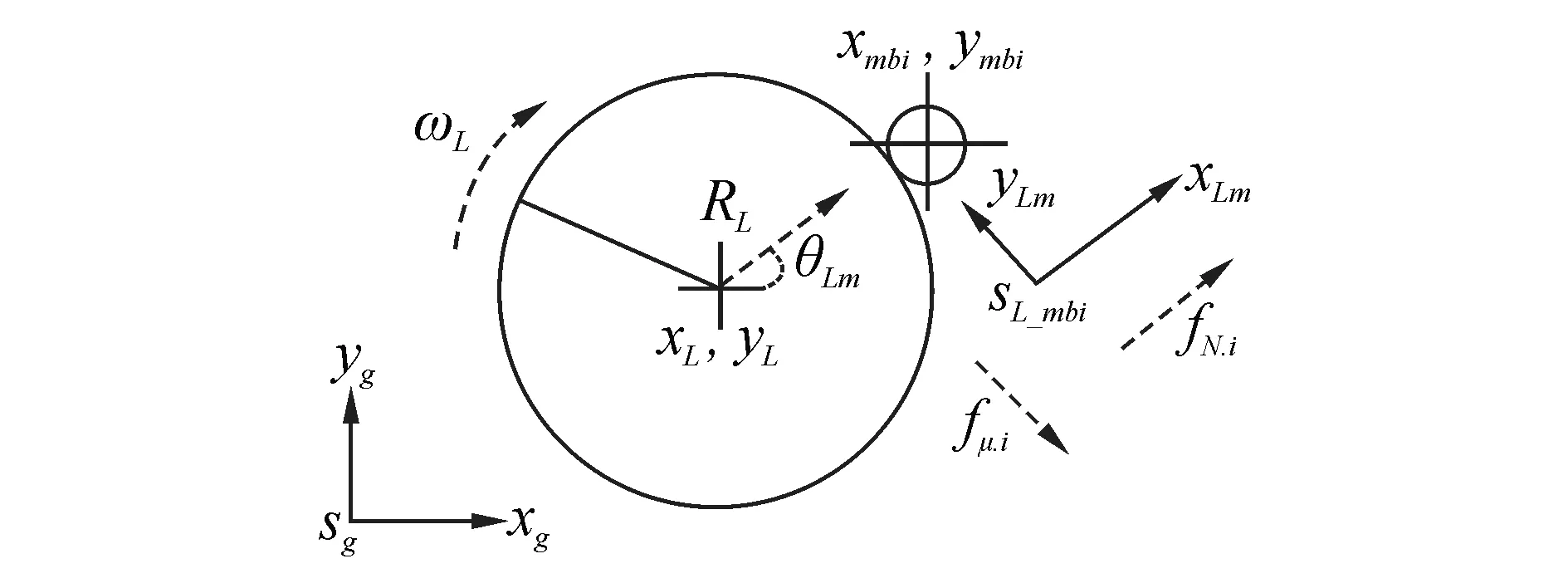
图8 XY平面滑轮与索球作用力关系

为了方便受力计算，根据质量球和索的位置关系，建立局部坐标系SLm，则在该局部坐标系内，滑轮对质量球的弹力恰沿着X轴方向，而摩擦力恰沿着Y轴方向。该坐标系与世界坐标系的XY平面的关系是旋转了角度θLm，由此得到从大地坐标系至该局部坐标系的变换矩阵如下：

(28)

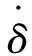
(29)

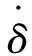
(30)

针对式(30)计算的相对速度ΔVL_mbi，利用坐标变换阵将其变换至局部坐标系表示：

(31)

代入变换阵后求得：

(32)

(33)

从而计算质量球与滑轮间的弹力如下：

(34)

式中：kδ_Lm和kη_Lm分别为质量球与滑轮的等效碰撞弹性系数和阻尼系数。

摩擦力计算：摩擦力分为动摩擦和静摩擦2种情况，需根据质量球与滑轮是否具有切向相对运动判断，即当|ΔVy.L_mbi.Lm|>0时采用动摩擦计算，否则采用静摩擦计算。

动摩擦大小与摩擦系数及压力有关，方向与索和滑轮相对滑移速度有关，从图8可知，索轮滑移速度及摩擦力均沿着SLm坐标系的Y轴方向，其符号相反，计算如下：

(35)

式中：μD_Lm为索与滑轮间的动摩擦系数，该摩擦系数受滑移速度影响，计算如下[12]:

(36)

式中：μD_min为最小动摩擦系数，μS_Lm为静摩擦系数。

静摩擦力的大小需根据该质量球所受的其他合外力而定：设质量球在不考虑滑轮对其作用力的情况下，受到左右相连弹簧的合力为FH.mi，首先利用坐标变换阵Lg.Lm将其从世界坐标系变换至局部坐标系SLm：

(37)

则静摩与FyH.mi_Lm符号相反，且当FyH.mi_Lm小于极限静摩擦力时，静摩擦与其大小相同，否则静摩擦大小即为极限静摩擦力，计算公式如下：

(38)

最终根据上文介绍的动、静摩擦判断条件，得出最终的摩擦力计算公式如下：

(39)

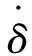
(40)

(41)

进一步计算滑轮槽限制力如下：

(42)

式中：kδZ_Lm和kηZ_Lm分别为质量球与滑轮槽的等效碰撞弹性系数和阻尼系数。

质量球受力合成：在前文引入的局部坐标系SLm内，滑轮对质量球的弹力沿其X轴方向向、摩擦力沿Y轴方向向、轮槽限制力沿Z轴方向，由此得到SL_mbi坐标系内质量球受到滑轮的合力FLm.L_mbi为：

(43)

在式(43)中分别代入式(34)、(35)和式(42)后，即为最终受力结果，最后利用前文给出的变换阵Lg.LmT，计算世界坐标系合力Fg.L_mbi，以便融入阻拦索有限元计算模型中：

(44)

滑轮受力合成：根据作用力与反作用力原理，可直接计算每个质量球对滑轮的反作用力，将所有与滑轮发生干涉的质量球受反作用力求和后，即可计算出阻拦索对滑轮的作用力Fg.mbi_L，将定从第m个球至第n个球与滑轮发生了位置干涉，那么有：

(45)

2.3.2 阻拦系统模型联立

本节利用文献[13]中阻拦系统中液压系统模型，通过压强计算方程描述阻拦系统主液压缸、滑轮缓存器及末端缓冲器的液缸压力，与阻拦索及滑轮系统一同构成完整的阻拦系统仿真模型。

为进一步实现阻拦系统的联动仿真，需计算阻拦索与液压缸滑轮组间的作用力，下面以主液压缸为例，给出计算过程：主液压缸一段连接定滑轮组，一段连接动滑轮组，阻拦索在其两端滑轮组上缠绕9圈。动滑轮组同时受到9圈阻拦索的张力作用和主液压缸的液压压力作用，合力FMEC计算如下:

(46)

式中：FY_g.mb_LMEC为所有与本滑轮位置干涉的质量球对滑轮合力Fg.mb_LMEC在Y轴的分量，Fg.mb_LMEC计算方法参考式(45)，PMEC为主缸压强[13]，SMEC为主缸横截面积。从而建立连接主缸的动滑轮组的动力学方程：

(47)

式中：MMEC为主缸动滑轮组系统质量；yMEC为主缸位移。而滑缓及末端缓冲滑轮与阻拦索的作用力计算过程同理。

3 阻拦过程综合仿真

为实现阻拦过程综合仿真，需建立尾钩与阻拦索的相互作用模型。尾钩钩头形状复杂，阻拦过程会与阻拦索发生复杂的碰撞和摩擦作用，为了简化仿真，借用前文滑轮与阻拦索作用模型，在尾钩末端引入一个虚拟滑轮如图9，利用虚拟滑轮与阻拦索间的作用力模型来模拟钩索过程钩与索的运动约束，虚拟滑轮位于尾钩末端，滑轮外沿与尾够末端顶点相切，且与尾钩运动固连。

与2.3.1节介绍的滑轮与索作用模型不同的是，前文中滑轮是水平或竖直摆放，而此处引入的虚拟滑轮需与尾钩一起运动，其六自由度位置及姿态均是实时变化的，此时，只需要将尾钩附近的弹簧质量球均变换至虚拟滑轮坐标系，并按照前文的方法计算其与滑轮的作用力即可，最终将虚拟滑轮受力代入尾钩动力学模型，并计算其对尾钩产生的附加力矩，最终便实现了挂索过程尾钩与阻拦索间的完整受力计算，从而实现了阻拦过程的综合联动仿真。

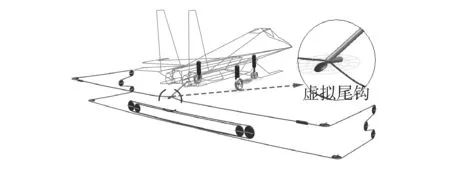
图9 飞机尾钩与阻拦索联合仿真

4 仿真结果

针对上文推导的模型，在VC++6.0平台上上实现了完整的阻拦过程仿真。针对飞机偏心阻拦过程仿真，设定飞机挂索速度220 km/h、飞机质量24.5 t，仰角8°，并以3.5°下滑角，挂索位置右偏4 m。图10给出了挂索初期的飞机和尾钩的运动轨迹，图11为阻拦过程左右滑轮缓冲位移曲线，图12为阻拦合力曲线，图13为主液压缸位移曲线，图14为左右末端缓冲位移曲线，图15为飞机横向位置变化曲线，图16、图17为尾钩的横向和纵向摆动角度曲线。

仿真结果看出，偏心阻拦导致左右侧受力不均，左右滑缓运动产生差别，左右末缓运动出现较大差别，飞机横向位置偏心继续向外侧增加，出现轻微的姿态横滚波动、尾钩出现复杂横向波动。

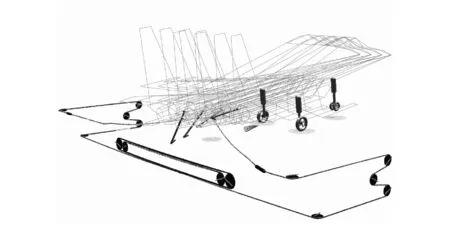
图10 偏心阻拦时挂索初期机体及尾钩运动轨迹

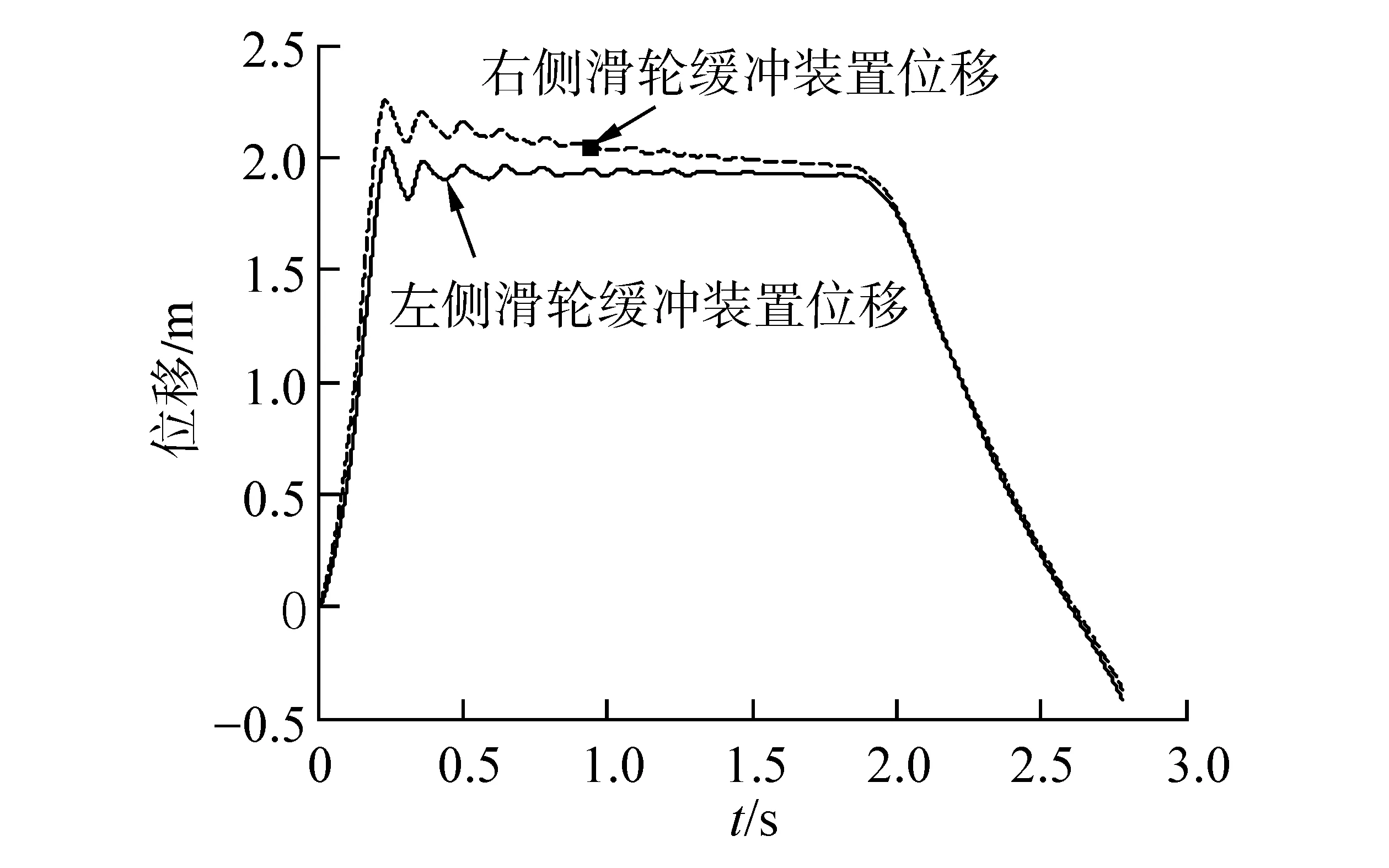
图11 偏心阻拦时滑轮缓冲仿真曲线

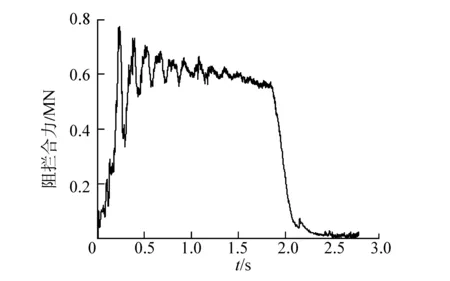
图12 偏心阻拦时阻拦合力曲线

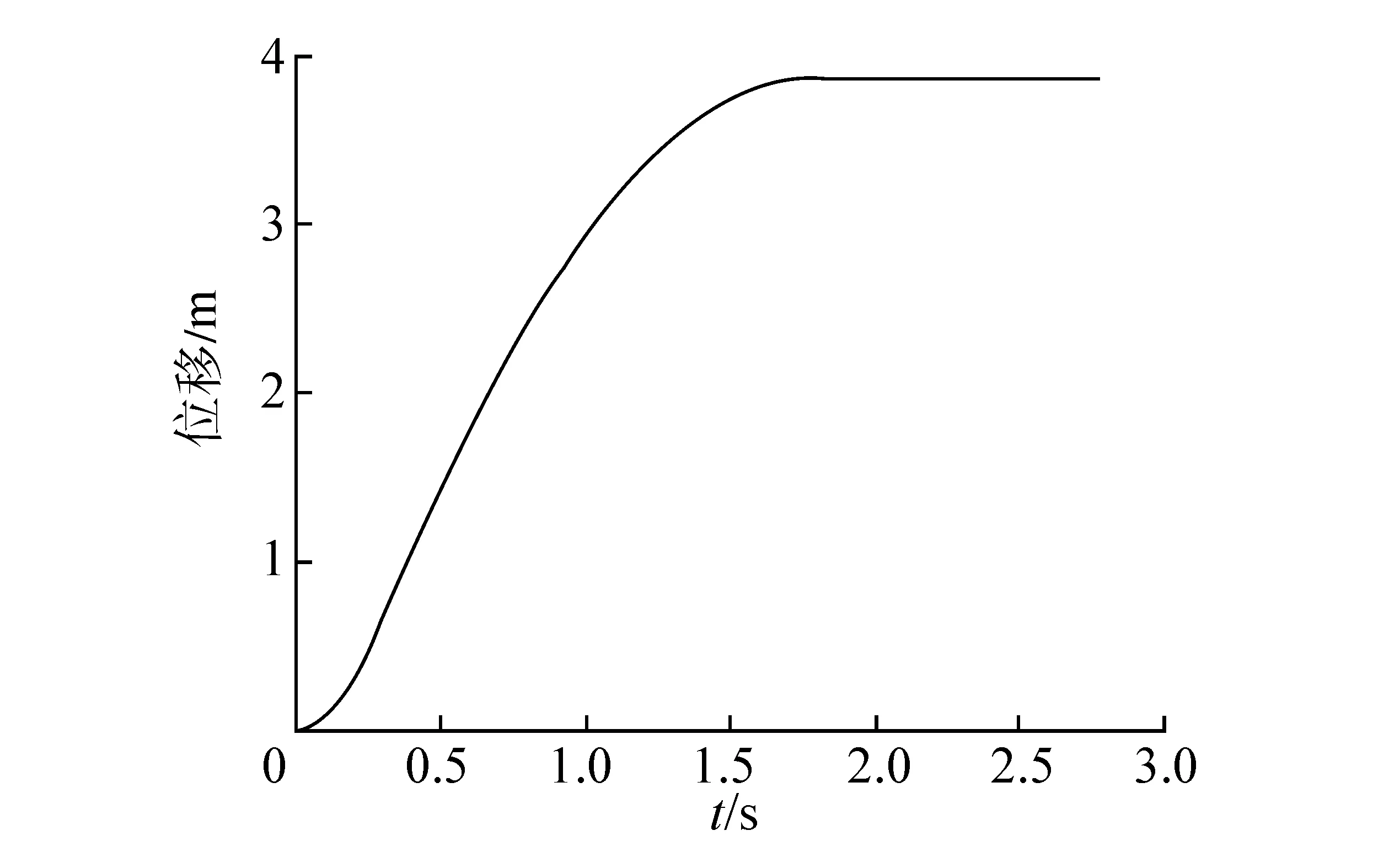
图13 偏心阻拦时主液压缸位移曲线

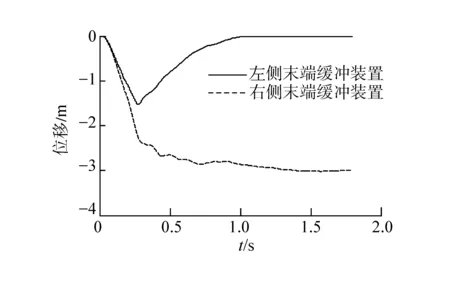
图14 偏心阻拦时左右末端缓冲系统位移

图15 偏心阻拦时飞机横向运动曲线

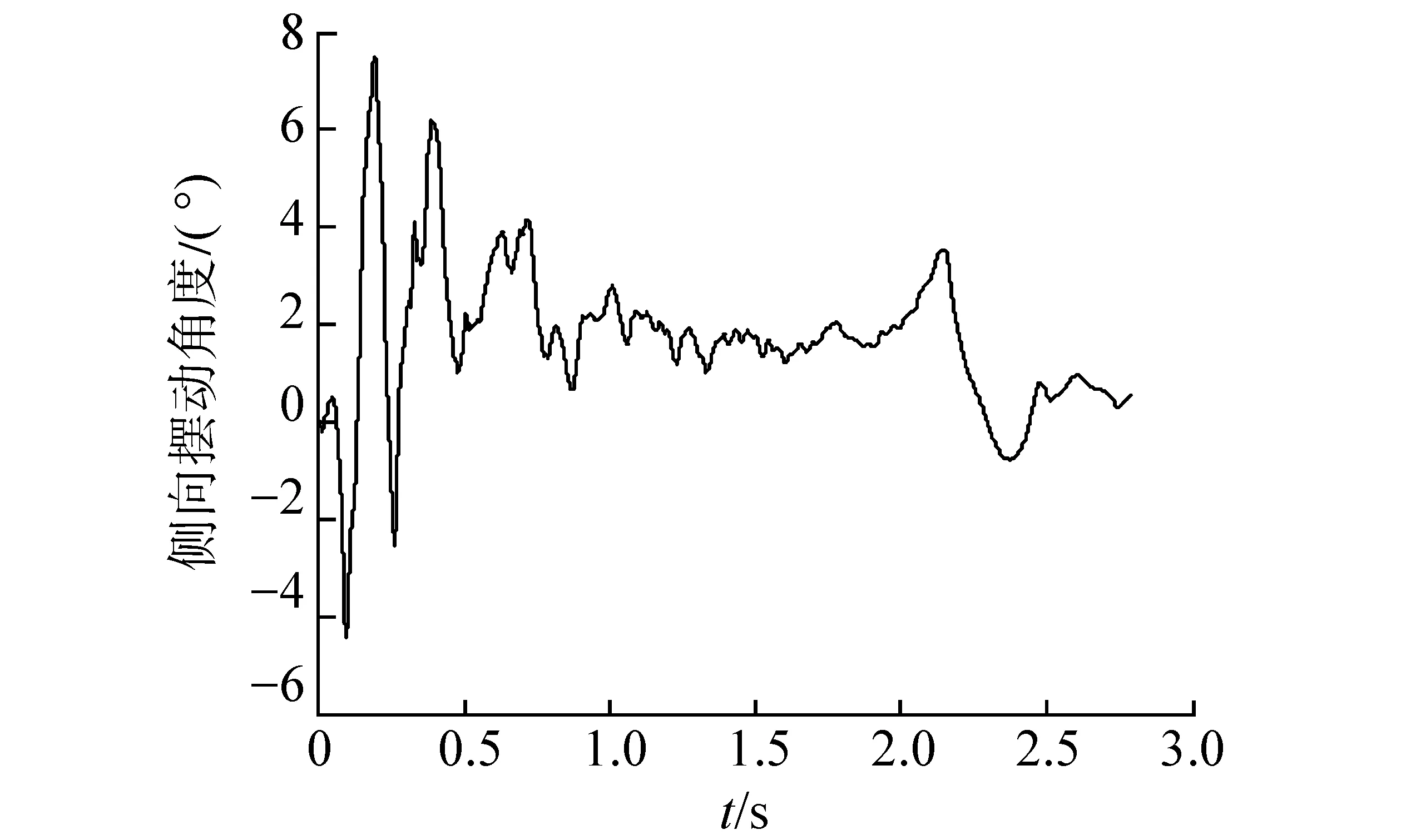
图16 偏心阻拦时尾钩横向摆动角度曲线

图17 偏心阻拦时尾钩纵向摆动角度曲线

5 结束语

本文建立的阻拦过程动力学仿真系统，能够体现飞机阻拦挂索的任意初始质量、速度、偏心、偏航、姿态、角速度等变化，并能体现挂索过程阻拦索的波动、阻拦钩的纵向和横向摆动、钩索滑移等规律，还能体现阻拦过程中左右索的受力不均、阻拦索上各部分应力变化、阻拦索的末端松弛、以及主液压缸、滑轮缓冲和末端缓冲系统的综合运动过程。本系统真正意义上实现了阻拦过程完整的动力学仿真，对研究阻拦过程各项规律具有重要意义，整个仿真系统在VC++平台上调试通过，并给出了阻拦过程多个环节的仿真曲线。在带有摇摆姿态的甲板上阻拦时，可将飞机位置、姿态及速度信息均变换至甲板坐标系，然后再应用本文方法仿真即可。

参考文献：

[1]BLACK R. A study in terminal bending of uniform and encapsulated eire rope with linear and non-linear constitutive equations[R]. Philadelphia,USA,1971.

[2]THOMLINSON J. A study of the aircraft arresting hook bounce problem[R]. American: R&M 2980, 1957.

[3]GIBSON P T, GRESSH A. Analytical study of aircraft arresting gear cable design[R]. American: AD617788, 1965.

[4]GIBSON P T, ALEXANDER G H, CRESS H A. Validation of design theory for aircraft arresting gear cable[R]. American: AD665328. 1968.

[5]柳刚,聂宏.飞机阻拦钩碰撞动力学和拦阻钩纵向阻尼器性能[J].航空学报，2009, 30(11): 2093-2099.

LIU Gang, NIE Hong. Dynamics of bounce of aircraft arresting hook impacting with deck and performance of arresting hook longitudinal damper[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(11): 2093-2099.

[6]柳刚.舰载飞机着舰阻拦钩碰撞及拦阻动力学研究[D].南京：南京航空航天大学，2010: 1-121.

LIU Gang. Investigation on arresting dynamics for carrier-Based aircraft with consideration of arresting hook bounce[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010:1-121.

[7]张萍,金栋平.计及弯折波的舰载机拦阻过程控制[J].南京航空航天大学, 2010,32(11):2008-2015.

ZHANG Ping, JIN Dongping. Control of arresting process for carrier aircraft considering kink-wave[J]. 2010, 32(11): 2008-2015.

[8]ZHANG Wen, ZHANG Zhi, ZHU Qidan, et al. Research on the dynamics model of carrier-based aircraft landing gears on the dynamic deck[J]. Chinese Journal of aeronautics, 2009,22(4):371-379.

[9]MATTHEWS F L, RAWLINGS R D. Landing signal officer reference manual[M]. Virginia Beach: Landing Signal Officers School Naval Air Station Oceana, 1999: I-11.

[10]KRAUT W K, SWIENCINSKI H J. Reliability of the mark 7 mod 3 arresting gear[R]. American: AD-845390, 1968.

[11]张澍森,金栋平.飞机阻拦过程的非线性最优控制[J]. 航空学报, 2009, 30(5): 849-854.

ZHANG Shusen, JIN Dongping. Nonlinear optimal control of aircraft arresting pross[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(5): 849-854.

[12]MIKHALUK D, VOINOV I, BOROVKOV A. Finite element modeling of the arresting gear and simulation of the aircraft deck landing dynamics[C]// European LS-DYNA Conference.Petersburg, Russia, 2008.31-35.

[13]朱齐丹,闻子侠,张智.阻拦系统动力学建模与仿真[J]. 航空学报,2012,33(3):520-529.

ZHU Qidan, WEN Zixia, ZHANG Zhi. Kinetic modeling and simulation of shipboard arresting system[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(3):520-529.