人体通信信道相位特性研究

张南南，杜文才，任 佳，聂泽东

(1.海南大学信息科学技术学院，海南海口570228;2.中国科学院深圳先进技术研究院，广东深圳518055)

1 人体通信信道

无线体域网(Wireless Body Area Network，WBAN)是以“个人”为中心，在不影响患者正常生活、学习和工作的情况下，通过将各种智能的、微型的和低功耗的传感节点放置在人体内、体表和人体周围，通过无线的方式在人周围建立无线个人局域网［1］。大部分的研究都采用现有的无线通信技术，如超宽带［2-3］、蓝牙、ZigBee［4］及其他工作在工业科学医用频段(industrial scientific medical，ISM)内的通信技术来实现人体近端通信。1996年来，美国麻省理工学院的Zimmerman提出了一种新的人体近端通信方式——人体通信(Human Body Communication ，HBC)［5］。HBC是以人体作为信号传输媒介从而实现信号在人体表面/内部的传输，因其所具有的低功耗、连接方便、不易受外界噪声干扰、高保密等特性对实现无线穿戴式医疗监护具有重要意义，引起研究者的广泛关注［5-7］。

人体通信信道特性研究对建立人体通信信道模型、人体通信收发器设计等具有重要意义。目前，有关人体通信信道特性的研究主要集中在人体周围的电磁场分布及人体等效电路模型［8-10］和电极大小、材质，传输频带，信道是否动态，调制方式等对通信质量的影响［11-12］。

然而，有关人体信道的相位—频率特性还未被广泛研究，信道相位—频率的非线性会导致符号间干扰，增大误码率，因此，本文通过测量人体信道群延时研究人体信号在1～200 MHz频段下的相位—频率特性，为后续人体通信样机设计提供参考。

以人体为通信信道实现信号传输是切实有效的，但信号在不同频率下的传播特性和能量分布范围是不同的。1～100 MHz频段内信号能较好地耦合到人体上，当载波频率大于100 MHz时，人体将被作为天线，信号将通过人体以电磁场与电磁波向周边辐射［13-14］。

为了更好地研究人体信道在不同频率下的相位特性及传播延时特性，选择合适人体通信频段，提高信号传播效率，也为高效收发系统的设计提供依据。本文选定研究频段为1～200 MHz，并将此频段分为2个研究子频段:1～100 MHz和100～200 MHz进行对比研究。

2 实验设置

2.1 群延时

时延是指信号通过通信系统所需要的传播时间。当一个单一频率的信号通过任意系统时，其传播时间可以通过输出信号相对于输入信号的相位移来计算。当复合信号(如发射机发送的调幅波)通过一个系统时，输出信号包络相对于输入信号包络的时延称为包络时延。因其涉及的是一群不同频率振荡在传输过程所表现的时延，故称为群延时，群延时Tg的数学表达式为

在无失真系统中，相位相对频率的响应是一个斜线，其导数是常数;如果相位对频率的响应是非直线，则其导数就不是常数，就会出现群延时失真，群延时在不同频率点上相对于平均值的波动幅度表示信号在此频率点上的相位畸变量。

2.2 实验场景设置

实验选定用安捷伦E5061A网络分析仪(Vector Network Analyzer，VNA)测量群时延，如图1a所示，志愿者静止站立在VNA前，并根据传播信道，在相应的身体部位绑上一对电极，图1b为4个传播路径及电极在人体上的绑定部位，分别是:左臂至右臂，左臂至右腿，右腿至左腿，左臂至左腿。图1c所示为测量中所用的4 cm×4 cm铜电极，VAN的发射端通过发射电极将信号耦合到人体，接收端通过接收电极将人体中信号传输至VAN的接收端。实验选择13名志愿者进行群延时测量，13名志愿者的体重范围为45～70 kg，身高范围为155～175 cm，平均年龄24岁，其中8名男性和5名女性，整个实验中志愿者被要求静止站立在测量仪器前。

3 实验结果

3.1 传播延时

图2为13名被测试者在1～200 MHz频段下，4个传播路径的平均延时。对同一测试者，4个传播路径下的传播延时基本相等;13名被测者中，10号和11号的延时测量结果与其他被测者差异较大，其中10号和11号的身高体重年龄与其他11名被测者均无明显差异，引起较大差异的具体研究，仍需进一步研究。即:1～200 MHz频段下，同一个体的传播延时与传播路径无关，多数个体的传播延时基本一致，个别个体存在较大差异。

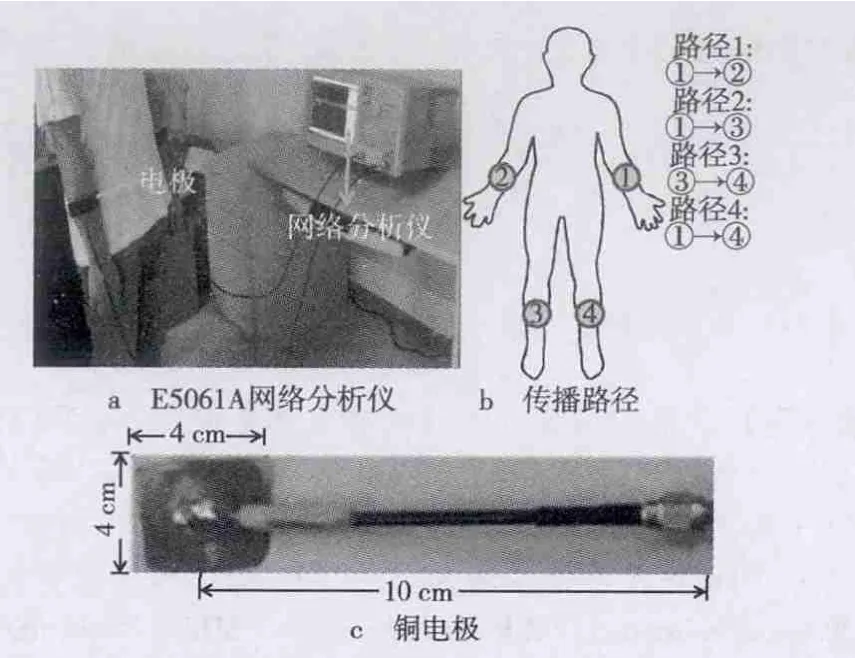
图1 实验场景

图2 1～200 MHz频段内4个路径下的传播延时

图3给出了在1～100 MHz和100～200 MHz频段下，4个传播路径的平均传播延时和标准偏差，其中误差棒代表标准偏差。表1给出了详细的数值描述。在1～100 MHz频段内，4个传播路径的平均延时几乎是相等的，例如，路径2具有最大的传播延时18.37 ns，路径4具有最小的传播延时16.86 ns，路径1和路径3的传播延时分别是17.06 ns和17.74 ns。4个传播路径中，最大的传播延时仅比最小的传播延时大1.56 ns。在100～200 MHz频段内，4个路径的平均延时基本相等，例如4个传播路径的传播延时分别是 15.23 ns，14.56 ns，15.14 ns，14.39 ns，其中最大的传播延时仅比最小的传播延时大0.84 ns。

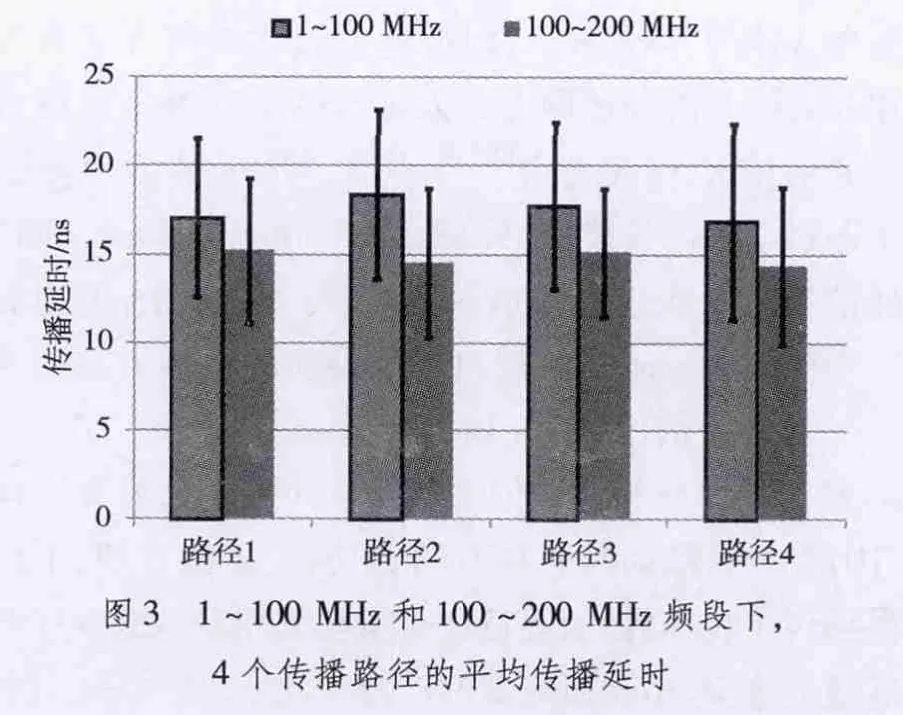
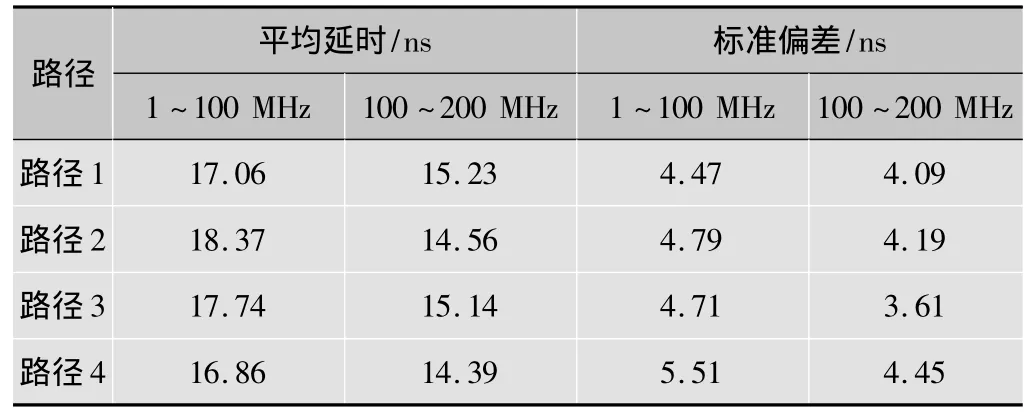
表1 不同传播路径下的平均延时及标准偏差

基于以上分析，在1～100 MHz和100～200 MHz频段内，信号的传播延时和传播路径无关，即信号在人体内传播延时和测量部位无关。1～100 MHz频段上的传播延时均比100～200 MHz频段上的传播延时大，此结果可能由于信号不同的耦合机制导致。

3.2 相位畸变

恒定的群时延代表线性相位。不同频点下，群时延偏离平均值的幅度值代表相应频点下相位的畸变大小。图4为1～200 MHz频段下的群延时测量图，图5为1～200 MHz频段内相位归一化统计结果图，归一化相位偏差值越大，表示在该频点下相位畸变越大。在20～40 MHz频段信号畸变较大。与1～100 MHz频段内的相位—频率特性相比，100～200 MHz频段内的相位—频率保持了较好的线性特性。

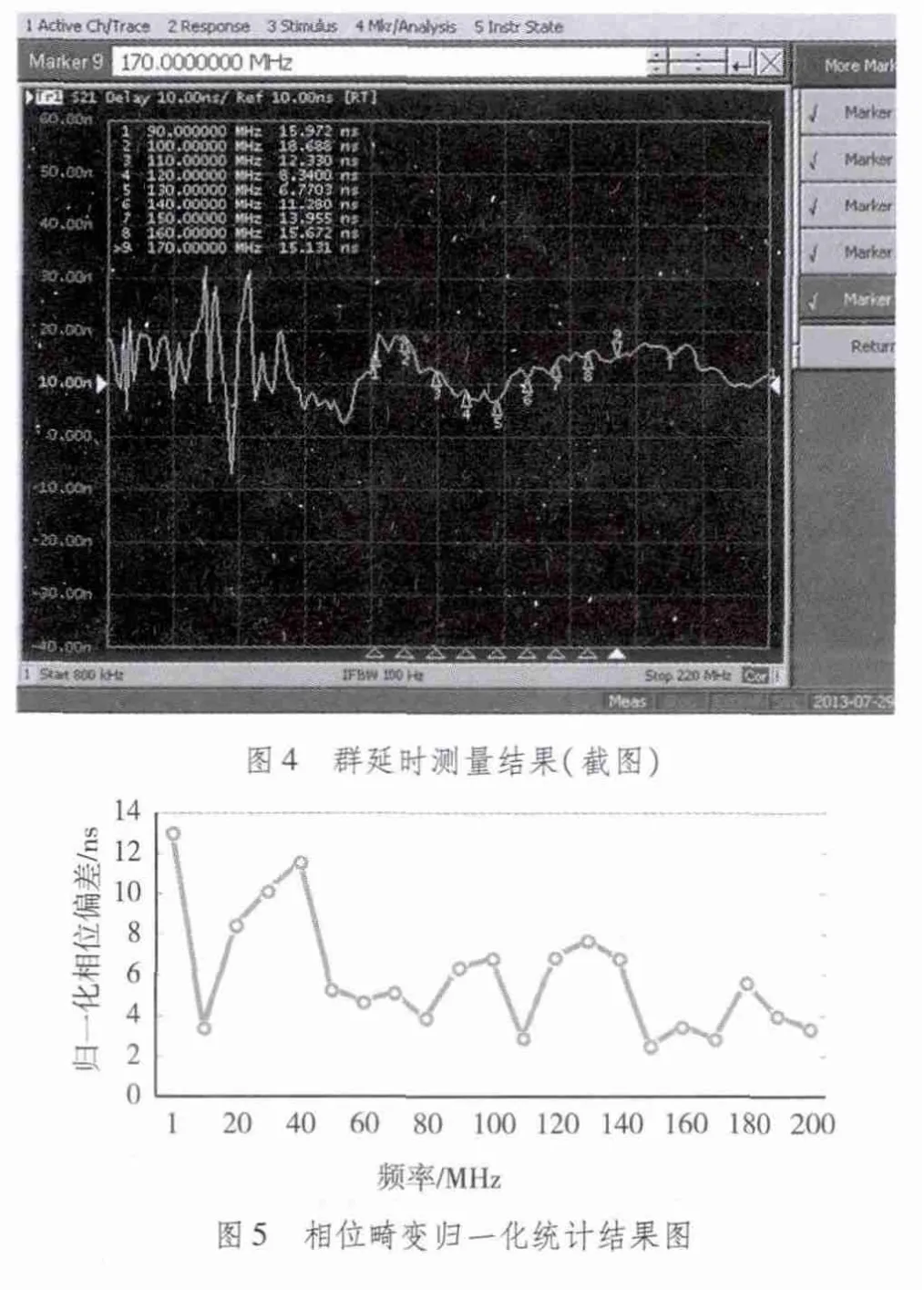
3.3 归一化相位畸变概率密度

为了精确描述人体通信信道相位特性，对1～200 MHz频段下信道相位畸变进行统计分析。分析中采用了3个常用的概率密度分布函数(Probability Density Functions，PDF):Lognormal，Gamma 和 Weibull分布对相位畸变归一化值进行拟合。通过最大似然估计算法(Maximum Likelihood Estimation，MLE)来估计分布参数，并通过Akaike(Akaike Information Criterion，AIC)信息准则来选择最佳分布模型［15］。图6所示为归一化相位畸变的概率密度函数(Probability Density Function，PDF)曲线及拟合模型。表1列出了分布模型和AIC、MLE参数。Lognormal分布具有最佳的拟合效果。所有参数的计算均在95%的置信区间内。

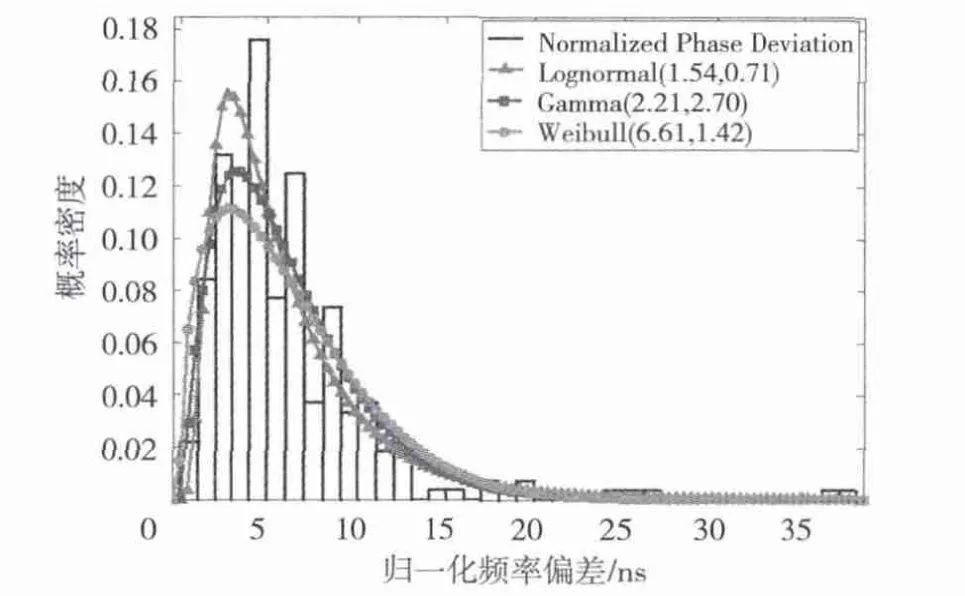
图6 归一化相位畸变概率密度和拟合模型图

表2 统计参数和分布模型

AIC公式定义为

式中:k是分布模型的参数;L是似然函数的最大值。

4 结论

本文主要通过实验统计的方法研究在1～200 MHz频段下人体通信信道的相位—频率特性。实验对13名志愿者分别进行4个传播路径群延时测量。统计分析结果表明，传播延时与传播路径无关。然而，1～100 MHz频段下的传播延时均比100～200 MHz频段下的传播延时大，由此推断此结果可能是由不同的耦合机制引起。

本文给出了1～200 MHz频段下，人体通信信道归一化相位畸变曲线，结果表明在20～40 MHz频段信号畸变较大，与1～100 MHz频段相比，100～200 MHz频段具有更优的相位—频率特性。根据MLE算法和AIC标准，Lognormal分布模型是归一化相位畸变概率密度函数的最佳拟合模型。

:

［1］ LATRE B，BRAEM B，MOERMAN I，et al.A survey on wireless body area networks［J］.Wireless Networks，2011，17(1):1-18.

［2］ ROELENS L，JOSEPH W，REUSENS E，et al.Characterization of scattering parameters near a flat phantom for wireless body area networks［J］.IEEE Trans.Electromagnetic Compatibility，2008，50(1):185-193.

［3］ ZHANG Y P，LI Q.Performance of UWB impulse radio with planar monopoles over on-human-body propagation channel for wireless body area networks［J］.IEEE Trans.Antennas and Propagation，2007，55(10):2907-2914.

［4］ MONTON E，HERNANDEZ J，BLASCO J，et al.Body area network for wireless patient monitoring［J］.IET Communications ，2008，2(2):215-222.

［5］ ZIMMERMAN T G.Personal area networks:near-field intrabody communication［J］.IBM Systems Journal，1996，35(3/4):609-617.

［6］ SEYEDI M ，KIBRET B ，LAI D T H，et al.A survey on intrabody communications for body area network applications［J］.IEEE Trans.Biomedical Engineering，2013，60(8):2067-2079.

［7］ WEGMUELLER M S，OBERLE M，FELBER N，et al.Signal transmission by galvanic coupling through the human body［J］.IEEE Trans.Instrumentation and Measurement，2010，59(4):963-969.

［8］ XU R，ZHU H J，YUAN J.Electric-field intrabody communication channel modeling with finite-element method［J］.IEEE Trans.Biomedical Engineering，2011，58(3):705-712.

［9］ FUJII K，TAKAHASHI M，ITO K.Electric field distributions of wearable devices using the human body as a transmission channel［J］.IEEE Trans.Antennas and Propagation，2007，55(7):2080-2087.

［10］ HAGA N，SAITO K，TAKAHASHI M，et al.Equivalent circuit of intrabody communication channels inducing conduction currents inside the human body［J］.IEEE Trans.Antennas and Propagation，2013，61(5):2807-2816.

［11］ SMITH D B，HANLEN L W，ZHANG J A，et al.First-and second-order statistical characterizations of the dynamic body area propagation channel of various bandwidths［J］.Annals of Telecommunications-annales Des Telecommunications，2011，66(3/4):187-203.

［12］ NIE Z D，MA J J，LI Z C，et al.Dynamic propagation channel characterization and modeling for human body communication［J］.Sensors，2012，12(12):17569-17587.

［13］ BALDUS H，CORROY S，FAZZI A，et al.Human-centric connectivity enabled by body-coupled communications［J］.IEEE Communications Magazine，2009，47(6):172-178.

［14］代鸿文.人体通信信号传输方式与特性研究［D］.杭州:浙江大学，2012.

［15］ BURNHAM K P，ANDERSON D R.Model selection and multi-model inference:a practical information-theoretic approach［M］.New York:Springer-Verlag New York，2002.