基于局部模式加权估计纹理分析的人脸识别

胡钟月

(广西现代职业技术学院，广西河池 547000)

由于人脸识别技术具有低干扰性和高精确性［1］，在很多场合下的应用都高于其他生物识别方法，包括一些大范围的应用，比如护照、驾驶执照鉴别、海关检查等［2］。

随着人脸识别技术的发展，基于纹理分析的方法得到了越来越多的应用。许多研究表明，纹理分析方法的应用能够超过其他人脸识别方法主要是因为其对正面照脸部表情的细节变化进行了处理［3］。纹理特征提取是成功进行图像纹理描述、分类与分割的关键环节，纹理特征的提取直接影响后续处理的质量。提取的纹理特征维数不大、鉴别能力强、稳健性好，且提取过程计算量小。在过去的30多年，很多纹理特征提取的方法被进一步发展。这些纹理特征大致分为基于统计特征、基于模板卷积特征、基于频域特征和基于模型特征这4类［4-7］。

杨关等人曾提出在纹理分析中构建高斯图模型(Gaussian Graphical Models，GGM)［8］，根据纹理特征的局部马尔可夫性和高斯变量的条件回归之间的关系，将复杂的模型选择转变为较为简单的变量选择，应用惩罚正则化技巧同步选择邻域和估计参数，实验显示了基于高斯图模型的纹理特征对纹理分析的有效性。但是，复杂的计算开销使其在应用中受到了限制。结合纹理编码，文献［9］提出了一种基于统一权值的纹理分析(Texture Analysis based on Union Weighting，UWTA)方法，采用一组实验步骤获得一个基于识别率的权值的固定形式，意识到了这些权值并不是最佳的，但是通过比较统一的权值，可以提高识别的能力。此后，大多数基于纹理的人脸自动识别的方法(Automatic Face Recognition，AFR)［10］都开始使用固定权值来进行人脸识别。文献［11］提出运用最小二乘法得出齐次非线性方程组，一定程度上提高了基于纹理编码的人脸识别率。并且通过实验表明，运用最小二乘法要比使用固定权值方法要好。然而，最小二乘法涉及到一个相当复杂的方程组，而且还要计算出大量样本图像的每一个被估计的权值。

根据上述分析，传统的纹理分析方法仅以每个脸部区域的相对贡献来标记全局相似度［12］，针对这种以局部表示全局而导致不能很好地进行特征提取的问题，本文提出了基于局部模式的加权估计纹理分析(Weighting Estimation for Texture Analysis，WETA)方法，使用局部二值模式(Local Binary Pattern，LBP)［13-14］或者局部相位量化(Local Phase Quantization，LPQ)［15-16］对相似空间中最具识别力的坐标轴进行纹理分析，并且利用编码与数据库的不同组合估算出权值，通过权值优化给出最佳解决方案。与最小二乘法相比，该方法中每个权值需要训练样本的数量更少，而且运算起来更高效，实验对两种纹理编码方式进行了详细的分析，验证了所提方法的有效性。

1 纹理编码

1.1 基于局部二值模式(LBP)的纹理编码

利用局部二值模式(LBP)来进行脸部描述，主要通过分配给x=(x，y)坐标的每个像素一个编码后，计算出来在半径为R的范围内，中心像素强度与离中心m等距像素强度之间的差别，决定如何分配编码。根据像素强度正负值之间的差别，分配二进制“0”和“1”，当采样点不符合中心像素时使用双线内插法。LBP纹理编码以一种无序而又固定的二进制串联方式组成，用“0”和“1”来表示m等距内的像素强度。图1包括了4张LBP的影像样本，从中可以看出像素强度与每个像素的LBP编码之间的关系。

图1 样图及相应的LBP、LPQ表示法

1.2 基于局部相位量化(LPQ)的纹理编码

实际应用中，局部相位量化(Local Phase Quantization，LPQ)方法要比LBP更好，因为LBQ图像更模糊，均匀亮度变化更大。与LBP相似，LPQ通过计算x=(x，y)坐标的每个像素编码，用编码代表以x为中心的M×M邻域内(Nx)的像素。

在4个低频区的Nx中观察傅里叶变换Fx(u)，u=(u，v)中的实值、虚值实现相位量化。在这里产生了8位二进制数，“0”和“1”的选择取决于每个值的正、负。这些二进制数随意而又固定地串联成了1个8位二进制数，以此描绘Nx中的纹理，图像中所有的像素都利用这种方法得出相应的LPQ图像表示。

此方法包括一个简单的过程:在量化步骤前解除傅里叶系数的关联，最大限度地保存纹理代码的信息。

2 加权估计纹理分析(WETA)

2.1 人脸匹配

假设人脸数据库中包含很多两眼清晰的图像，而且图像中眼睛的像素坐标也相同，数据库中用Sir表示第i个对象的第r个图像。识别过程中纹理图像将被划分成大小相等且不重叠的从1到B的区域，其中，第b块区域纹理编码的直方图统计中，b=1，2，…，B。

第b块区域中，bHir和bHjt这2个直方图的差别在于图像Sir和图像Sjt用不同的距离函数bdirjt(bHir，bHjt)计算，文中简述为bdirjt。

利用计算直方图间距的线性组合来测量脸部的全局相异度，从而推断出2张人脸是否来自同一个人，即

式中:系数wb为权值，表示第b块区域与最终识别一致的相对相关性。

2.2 权值估计

所提方法主要的工作是估计wb系数，并且对式(1)进行重新阐释，达到权值最优化的目的。把B区域中的Sir和Sjt脸部图像间的直方图间距进行组合，其向量dirjt=［1dirjt，2dirjt，…，Bdirjt］代表B维中的相似空间。进一步组合wi's系数，其向量为w=［w1，w2，…，wB］。式(1)可采取以下形式

因此，全局相异度测量的方法是利用系数向量w来定义相同空间内一个方向的距离向量dirjt。假定最佳加权与相同空间的方向相符合，那么就可以尽可能地把相同对象的配对图像从不同对象的配对图像中分离出来。

如果假定这2种类型图像对的协方差矩阵是相等的，则可以直接使用Fisher准则来找出最佳加权式中和分别是不同对象中配对图像的平均距离向量是协方差矩阵的合集。许多文献中的多元统计分析报告指出，甚至在协方差的假设不成立的情况下，Fisher准则仍然是很有效的。

通过式(3)快速计算权值是非常重要的，一般情况下，它并不遵循从左到右的脸部对称性。然而，通过二等分系数的量值去估计，则可以用来执行权值对称，降低问题的复杂程度。假设区域b，(b+B)/2，甚至B，与对称的脸部区域相符合，则可以令bw=b+B/2w使得权值对称，如此，式(1)就可以改写为

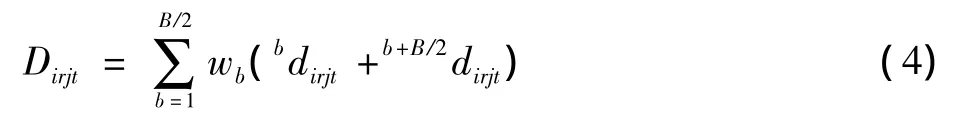
如此，解决了权值估计问题，也就解决了权值最优化问题。

2.3 相似性度量距离转换

采用的相似性度量是一个人脸识别中的局部模式基础方法，它将人脸图像分为一个常规的单元格和与局部模式一致的单元格，最后在人脸识别中的χ2分布上采用最近相邻分类法

式中:p，q分别是图像区域描述符(直方图向量)。

由于不重合的原因，给出所有编码值的目的是为小空间偏差提供光照和离群强健虚拟一致，使用类豪斯多夫距离相似性度量似乎是合适的，即采用图像中每个LBP或者LPQ编码，并测试一个相同的编码是否出现在图像的相近位置上，加权随着图像距离而平滑下降。为了实现区别性基于外貌图像和易于控制的空间松弛度的匹配，可以采用距离转换方案。给出一个二维的参考图像，可以找到二进制或三进制编码的图像，然后将其转化为稀疏二进制图像集，对应每个可能二进制或三进制编码值(例如一致编码的59张图像)。每个编码指定它的特别二进制或三进制编码值的像素出现的位置，然后计算它的距离转换图像。每个像素点给出了带有编码的最近图像的距离，图像与图像之间的距离或者相似性度量可以表示为

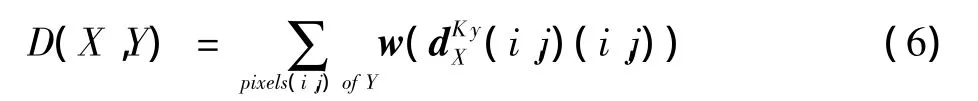
它是图像像素点的编码值，也是一个自定义的函数，它将损失传递给最近匹配编码中的给定空间距离上的一个像素点，所有的全局人脸在一些像素点内对齐，默认参数值是像素点。

2.4 所提方法整个过程

所提方法的整个过程如图2所示，首先利用LBP或LPQ对人脸图像进行纹理编码，然后将纹理图像划分成B个大小相等且不重叠的区域，接着利用Fisher判别分析方法估算出权值系数wb，b=1，2，…，B，并利用式bw=b+B/2w对称权值，当读入一个测试图像时，进行相同的操作，最后利用直方图间距的线性组合进行全局相异度测量，计算测试图像与训练图像之间的欧式距离，最后，利用k近邻分类器完成人脸的识别工作。

3 实验

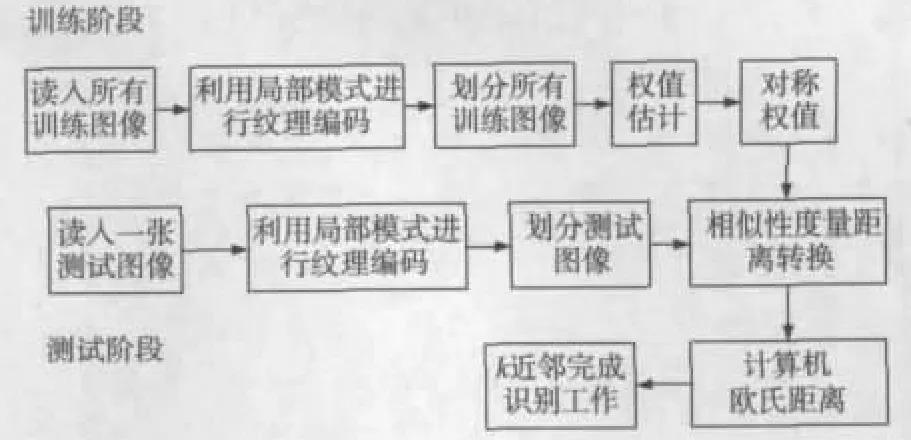
图2 所提方法实现过程

所有的实验均在4 Gbyte内存Intel(R)Core(TM)2.93 GHz Windows XP机器上完成，编程环境为MATLAB 7.0。

3.1 人脸库

FERET人脸库包含200个人的1 400张图像，每人7张，它们是在不同的表情、视觉角度及其光照强度下拍摄的，如图3所示为FERET上某个人脸的7张图像。

图3 FERET上某人的7张人脸图像

ORL人脸库共有40个人的400张图片，每人10张，其中有些图像拍摄于不同的时期，人的脸部表情和脸部细节有着不同程度的变化，如图4所示为ORL上某人的10张图片。

图4 ORL人脸库中某人的10张人脸图像

3.2 实验结果

实验中，图像均被转换为80×64像素分辨率，右侧和左侧眼睛的像素坐标值分别为(20，14)和(20，51)。采用统一的LBP变量图像，图像含有8个采样点(m=8)，半径长为2个像素点(R=2)。计算每一个7×7的像素邻域(M=7)，且在频率值a=1/7时执行相位量化，通过计算大小为8×8像素中超过10×8个非重叠区域，得到2个数据库的直方图。

选取FERET及ORL中每人的前5张人脸图像用于训练，剩下的用于测试，训练阶段利用不同数据库与编码的4种组合估算权值，包括LBP-FERET，LPQ-FERET，LBP-ORL，LPQ-ORL，测试阶段利用相同的4种组合进行识别率的计算，这样估算权值与测试就有16种不同的组合，利用距离转换度量计算测试图像与各个训练图像之间的距离，采用k近邻分类器完成识别，其中，k值取3，图5列出了各种组合加权取得的最好的5个识别率，小图中每个标题显示了用于估算权值的编码与数据库的不同组合。

图5 不同数据库和编码技术配置得出的识别率

从图5可以得出16种组合的最佳识别率，如表1所示，其中，横向表示训练阶段估算权值的编码与数据库的不同组合，纵向表示测试阶段的编码与数据库的不同组合。

表1 16种不同组合取得的最佳识别率 %

从表1可以看出，在相同的人脸数据库上使用相同的纹理编码可以获得最好的表现效果，在不同的人脸数据库上使用不同的纹理编码取得的效果最差。其中，在FERET人脸数据库上取得的最佳识别率为97.92%，在ORL人脸数据库上取得的最佳识别率为99.19%，接近100%。同时可以看出，不管是训练还是测试，LBP与LPQ两种编码技术在同一数据库互相转换，对实验效果的影响都很小，与此相反，当利用某个数据库估算权值而又在另一个数据库上进行实验时，识别效果明显下降。

3.3 比较与分析

为了更好地体现所提方法的优越性，这部分比较了所提方法与其他文献中的方法，包括 PCA［2］、LDA［4］、LBP［5］、LPQ［6］、PCA-NN［7］、高斯图模型(GGM)［8］、基于统一权值的纹理分析方法(UWTA)［9］和基于最小二乘法(Least Squares)的纹理分析方法［11］，分别在FERET和ORL数据库中用LBP和LPQ纹理编码对识别率进行了测试，各个比较方法的参数设置均与各自的文献相同，实验结果取FERET及ORL人脸数据库中每个人的前5幅图像用于训练，剩下的图像用于测试，详细实验结果如表2所示。

从表2可以看出，在各种组合情况下，在FERET及ORL两大人脸库上，所提方法的识别率明显高于其他各个方法，在 FERET上，所提方法比 PCA、LDA、LBP、LPQ、PCA-NN、GGM、UWTA、基于最小二乘法的纹理分析方法的识别率分别高了9.92%、5.71%、3.20%、2.09%、1.62%、1.13%、0.84%、0.60%，在 ORL上，所提方法比PCA、LDA、LBP、LPQ、PCA-NN、GGM、UWTA、基于最小二乘法的纹理分析方法的识别率分别高了7.37%、4.82%、3.62%、2.29% 、2.33% 、1.95% 、1.60% 、0.99% 。

通过引入加权估计，LBP、LPQ的识别率明显提高了很多，进行比较的GGM、UWTA、基于最小二乘法的纹理分析方法都是比较先进的纹理分析方法，所提方法的识别率明显高于这三种纹理分析方法，也正是因为所提方法引入了加权估计，才达到了比较好的识别效果，足以体现了所提的加权估计纹理分析方法的优越性。

表2 各方法在FERET及ORL上识别率的比较 %

4 总结

本文提出了基于局部模式的加权估计纹理分析来估算最佳面部区域的权值，在FERET及ORL两大人脸数据库上进行了实验，利用2种不同的纹理编码技术，通过对本文方法与最近类似文献中其他纹理方法的比较，表明了所提方法在识别性能方面的优越性。实验结果表明，在给定的应用中，所提方法能够捕捉到人脸图像中可能出现的分类的不对称性，例如非对称的视差发光格栅。

对LBP及LPQ进行纹理编码后，进行纹理图像划分、权值推断、权值对称，明显提高了人脸识别率，但同时也增加了额外的开销，所以，如何在提高识别率的前提下提高算法的效率，将是进一步研究的重点。

:

［1］孙吉贵，刘杰，赵连宇.聚类算法研究［J］.软件学报，2008，19(1):48-61.

［2］乔立山，陈松灿，王敏.基于相关向量机的图像阈值技术［J］.计算机研究与发展，2010，47(8):1329-1337.

［3］KOLDA T G，BADER B W.Tensor decompositions and applications［J］.SIAM Review，2009，51(3):455-500.

［4］王佳奕，葛玉荣.基于Contourlet及支持向量机的纹理识别方法［J］.计算机应用，2013，33(3):677-679.

［5］ZHAO Q，ZHANG D，ZHANG L，et al.High resolution partial fingerprint alignment using pore-valley descriptors［J］.Pattern Recognition，2010，43(3):1050-1061.

［6］ZHAO Q，ZHANG D，ZHANG L，et al.Adaptive fingerprint pore modeling and extraction［J］.Pattern Recognition，2010，43(8):2833-2844.

［7］SU Y，SHAN S，CHEN X，et al.Adaptive generic learning for face recognition from a single sample per person［C］//Proc.IEEE International Conference on Computer Vision and Pattern Recognition，2010.［S.l.］:IEEE Press，2010:2699-2706.

［8］HU H.Orthogonal neighborhood preserving discriminant analysis for face recognition［J］.Pattern Recognition，2008，41(6):2045-2054.

［9］杨关，冯国灿，陈伟福，等.纹理分析中的图像模型［J］.中国图象图形学报，2011，16(10):1818-1825.

［10］XIE Z，LIU G，FANG Z.Face recognition based on combination of human perception and local binary pattern［J］.Lecture Notes in Computer Science，2012，72(2):365-373.

［11］CONNOLLY J F，GRANGER E，SABOURIN R.An adaptive classification system for video-based face recognition［J］.Information Sciences，2012，192(1):50-70.

［12］文乔龙，万遂人，徐双.Fisher准则和正则化水平集方法分割噪声图像［J］. 计算机研究与发展，2012，49(6):1339-1347.

［13］ARANDJELOVI O.Computationally efficient application of the generic shape-illumination invariant to face recognition from video［J］.Pattern Recognition，2012，45(1):92-103.

［14］ZHANG Z，WANG J，ZHA H.Adaptive manifold learning［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2012，34(1):131-137.

［15］HAFIZ F，SHAFIE A A，MUSTAFAH Y M.Face recognition from single sample per person by learning of generic discriminant vectors［J］.Procedia Engineering，2012(45):465-472.

［16］LOWE D.Distinctive image features from scale-invariant key points［J］.International Journal of Computer Vision，2004，60(1):91-110.