基于子集矩阵的LDLC短环消除方法

朱联祥，李 想

(重庆邮电大学信号与信息处理重庆市重点实验室，重庆 400065)

20世纪60年代，Gallager在其博士论文中提出了低密度奇偶校验码(Low Density Parity Check，LDPC)［1］。在二进制域的有限字符信道上，拥有一定结构的简单码字能够有效地接近信道容量［2］，LDPC码符合这一要求。随着Mackay［3］对LDPC码的重大发现，LDPC码在近几十年凭借其优良的性能得到了越来越广泛的关注。受LDPC码的启发，2007 年，N.Sommer，M.Feder和 O.Shalvi提出了低密度格码(Low Density Lattice Codes，LDLC)［4］。LDLC码将码字定义在格域［5－6］，具有较低的编码复杂度以及良好的译码收敛性，并且同样能够接近香农限，因此LDLC码具有广阔的应用前景。

在信道编码中，编码是非常重要的一环，想要进行高效的译码，就必须首先得到合适的码字，而码字要通过校验矩阵得到。校验矩阵中环结构的存在，尤其是短环，会影响迭代译码时外部交换信息的独立性，并且在若干次的迭代译码后会因为互相关性而大大降低译码的收敛速度，严重影响译码的效率以及准确度。为了能够有效地消除短环(4环以及6环)，本文提出了一种基于子集矩阵的短环消除方法。使用该方法消除短环，具有很低的计算复杂度，同时仿真结果表明，使用这种方式去环，能够很大地改善码字的译码性能。

1 LDLC中H矩阵与Tanner图的关系

编码去环时，通常是借助Tanner图来观察校验矩阵H中校验节点和变量节点之间的关系，然后利用相关的算法达到去环的目的［7］。H矩阵中，变量节点对应着码字，校验节点表示校验矩阵的某一行。Tanner图中，校验节点和变量节点分属两个区域，若第i行第j列元素非0，Tanner图中校验节点i就与变量节点j相连［8］。与LDPC码不同，LDLC校验矩阵中的非0元素取值不全为1，而是首先确定一个生成序列，H矩阵中非0元素的取值就是生成序列中元素的值。非0元素的取值有两个原则:第一，每一行每一列的元素不相同;第二，赋值后随机给非0元素添上正负号。一个度为3的5阶H矩阵，若生成序列为{0.3，0.5，1}，该 Tanner图如图1 所示，H 矩阵为

2 基于子集矩阵的短环消除算法

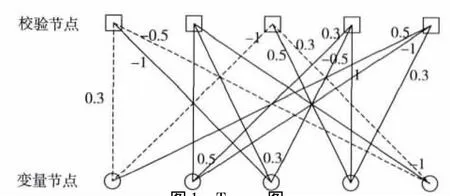
图1 Tanner图

基于Tanner图可以看到环的存在，如图1所示，存在4环(虚线部分)。环是由某一个节点开始并且由这个节点结束过程中所经过的路径，通常将所有可能环的最短长度称为Girth。迭代译码算法中，当校验节点和信息节点进行信息传递时，如果传递的信息不包含上一轮迭代过程中节点的信息，此时的译码效率最高。但是环一定存在，经过若干次迭代以后，某一个节点一定会接收到自身的信息。环的存在破坏了迭代译码中外部信息交换的独立性，所引起的互相关性不仅使得收敛过程变的缓慢，同时译码过程中产生的误比特信息会通过环放大返回给这个比特，破坏了算法的简洁性且影响了纠错算法的正确性。学者通过实验得到［4］，在LDLC中，破除6环以后，破除更大的环并不能给译码性能带来明显的提高，因此本文将重点放在破除4环以及6环上。

LDLC的编码去环方法已经有一些学者进行了研究，其中主要有穷尽搜索［4］以及准循环搜索［9］两种。前一种方法计算量太大，而且仿真表明在码长大于100时，完全消除4环非常困难。准循环的方法大大降低了复杂度，但是这种方法的码长构造并不灵活，而且计算复杂度也会随码长的增加而增大。

2.1 LDLC中的子集矩阵

子集矩阵是将校验矩阵的变量节点和校验节点各自分成一定数量的子集，并且每个子集中的节点个数相等。每个子集中元素的个数称为Base1，若矩阵的阶数为R，则变量和校验节点均分为了R/Base1个子集，Base1应该被R整除。当知道了校验子集和变量子集的个数，可以得到子集矩阵的大小，这里子集矩阵S的阶数为R/Base1，子集矩阵中元素的取值范围是0～(Base1－1)。

子集矩阵S中，某个元素的取值就是校验子集中各校验节点与变量子集中各变量节点的相对位置连接关系。若Si，j=k，0≤k≤(Base1－1)，校验子集Ci与变量子集Vj中元素的连接关系为 {Ci，m，Vj，n}，1 ≤m≤Base1，1 ≤n≤Base1，那么有

式中:mod是模Base1计算。

已知一个3阶S矩阵，且Base1取值为5。由矩阵和可以得到H的Tanner图，如图2所示。Tanner图的上半部分是校验节点子集，下半部分是变量节点子集。S矩阵为

图2 由子集矩阵得到Tanner图

子集矩阵S是一个全元素3阶矩阵，因此由该Tanner图能够得到一个度为3的15阶H矩阵。H矩阵的度d与子集矩阵S的阶数相同。

2.2 LDLC中消除4环、6环的方法

图2是一个较为复杂的Tanner图，但是依靠子集矩阵可以得到该 Tanner图中 Girth的大小。J.Lu和 J.M.F.Moura在文献［10］中证明了Tanner图中Girth的大小由S矩阵封闭路径中各个元素大小关系决定，将这些元素进行mod运算，通过判断结果是否为0，可以得到Girth的值。对于S中任意封闭路径长度为k的k个元素s1，s2，…，sk，若

则该矩阵的Tanner图中没有k环存在［11］，这里的mod是模Base1计算。因此，对所有封闭路径长度为6的6个元素进行对应的运算，如果所有的计算结果都不为0，那么Tanner图中没有6环存在。

在S中清除4环非常容易，清除了以后可以得到无4环H矩阵。6环的可能情况有8种，如图3所示，清除4环后，最后两种6环情况不存在。在S中直接清除6环比较困难，去环过程中很容易产生新的4环和6环。本文利用两个子集矩阵S1、S0以及Base1、Base2分两步去除4环以及6环，得到无6环度为d的H矩阵。

图3 封闭路径长度为6的8种情况

d值通常较小，选定一个较小的Base1给S1矩阵赋值，S1矩阵的阶数为d。利用穷尽搜索法迅速消除d阶S1矩阵中的4环，由式(2)得到H1的Tanner图，然后能够得到矩阵H1，H1无4环。选定Base2，给H1中的元素1赋值，元素0不参与计算，赋值完毕后，H1变为另一个子集矩阵S0。S0中封闭路径长度为6的情况有8种，如图3所示。任取S0中所有封闭路径长度为6的6个元素，进行式(5)计算，如果为0，某个元素自增1，循环若干次，直到S0中的6环被完全去除。再由式(2)及S0得到H0的Tanner图，最终可以得到度为d的无6环校验矩阵H0。算法描述如图4所示。

2.3 无4环、6环LDLC码的实现

要生成一个码长为1 000、度为5且无6环的LDLC码。首先选定一个较小的Base1，令Base1=5，然后随机生成一个d阶矩阵S1，S1中元素取值范围为0～(Base1－1)，用穷尽搜索法完全消除S1中的4环。无4环S1可表示为

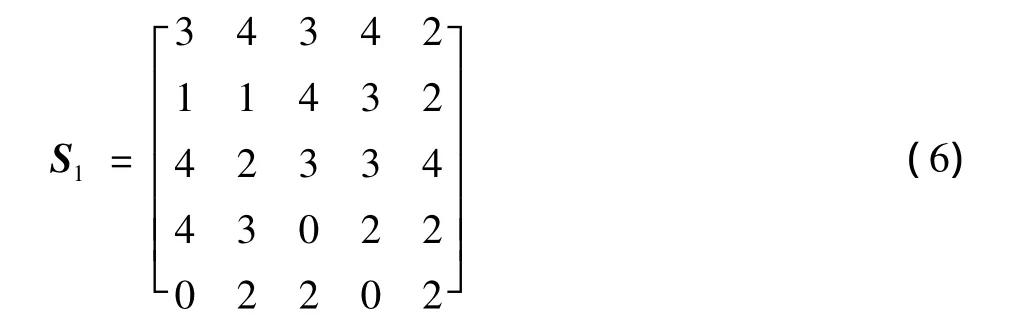
S1中无4环存在，那么能得到一个d·Base1=25阶无4环H1矩阵。

LDLC码利用位置矩阵表示校验方阵，位置矩阵的列数和方阵的列数相同，行数是方阵的度d。位置矩阵第i列的d个取值分别为方阵第i列所有非0元素的行数。由S1可以得到H1的Tanner图，根据这个Tanner图可以得到H1的位置矩阵h1，如图5所示。

由h1得到H1，此时H1没有4环，存在6环，因此将H1转换为另一个子集矩阵S0。要构造一个码长为1 000的LDLC码，Base2的取值为1 000/(d·Base1)=40。S0是一个25阶矩阵，度为5，将所有的非0元素进行0～(Base2－1)的随机赋值，零元素用N代替(不参与运算)。用图4的算法消除6环，可以得到无6环的矩阵，如图6所示S0。

图4 算法描述

图5 位置矩阵

S0矩阵已经消除了6环，结合Base2的取值得到这个子集矩阵所对应的Tanner图，由Tanner图就得到无6环，度为5，码长为1 000的校验矩阵H0以及H0对应的位置矩阵h0。H0的输出结果如图7所示(横坐标为校验矩阵的列，纵坐标为校验矩阵的行)。

图6 无6环子集矩阵

图7 无6环LDLC校验矩阵

H0是无6环的校验矩阵，但是与LDPC不同的是，此时的H0还不能参与译码计算，因为在LDLC中，校验矩阵中非0 元素的值应从生成序列中取得。{r1，r2，r3，r4，r5}是生成序列的5个值，在对H0的非0元素赋值时，应该保证每一行和每一列没有重复的赋值，赋值完毕以后，再给这些非0元素随机赋上正负号［4］。接下来对H0进行标准化处理，让H0的行列式为1。经过上述步骤处理以后的H0可以参与译码。

3 仿真结果

在本文的仿真中，度为5的LDLC码所选取的生成序列为{1/2.31 1/3.17 1/5.11 1/7.33 1/11.71}。仿真码长分别为500和1 000，仿真环境为无功率限制的高斯白噪声信道［12］，概率密度函数的分辨率Δ=1/64，译码帧数为250，译码的迭代次数为50，误比特率作为仿真结果的纵坐标，信号噪声σ2与香农限的距离(dB)为横坐标。

本仿真所选取的同一码长的LDLC码分别是用穷尽搜索去除4环和利用子集矩阵消除6环得到的，仿真结果如图8所示。可以看到，去除了6环的LDLC码(4环也被完全清除)的译码性能明显好于只去除了4环的LDLC码，这说明本文基于子集矩阵的方法能够有效消除短环。

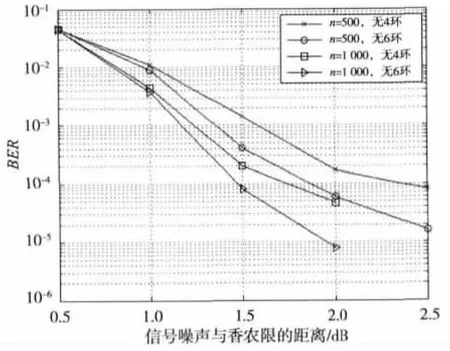
图8 仿真结果

4 小结

本文采用基于子集矩阵的方法消除LDLC码中存在的4环和6环，与穷尽搜索的方法相比，本文计算复杂度大大降低，并且可以保证不产生新的短环。与准循环的方法相比，在构造码长较大的LDLC码时，本文的方法更具有优势。

采用基于子集矩阵消除短环的方法，复杂度并不取决于码长，而是基于S0矩阵，S0仅与度数d以及Base1有关，即使码长增加，去除6环的步骤仍然在S0中进行，与码长的大小无关。随着码长的增加，虽然存在额外的运算量，不过该部分运算量很小，可以忽略不计。

当无6环存在时，选定的值可以构造任意长度的LDLC码，而算法复杂度不会增加，这是本文算法的一大优点。

采用基于子集矩阵消除短环的方法可以灵活得到各种长度的码长，并且具有更低的复杂度和较好的译码性能，这对于LDLC码的推广和应用具有积极的意义。

:

［1］GALLAGER R G.Low－density parity－check codes［J］.IRE Trans.Information Theory，1962，8(1):21－28.

［2］SHANNON C E.A mathematical theory of communication［J］.ACM SIGMOBILE Mobile Computing and Communications Review，2001，5(1):3－55.

［3］MACKAY D J C，NEAL R M.Good codes based on very sparse matrices［EB/OL］.［2013－05－10］.http://link.springer.com/chapter/10.1007/3－540－60693－9_13#page－1.

［4］SOMMER N，FEDER M.Low density lattice codes［J］.IEEE Trans.Information Theory，2008，54(4):1561－1585.

［5］RUDE D B.The upper error bound of a new near－optimal code［J］.IEEE Trans.Information Theory，1975，21(4):441－445.

［6］RUDI D B.Some optimal codes have structure［J］.IEEE Trans.Information Theory，1989，7(6):893－899.

［7］BOUTROSJ，POTHIER O，ZEMOR G.Generalized low density(Tanner)codes［C］//Proc.IEEE International Conference on Communicaitons.Vancouver，BC:IEEE Press，1999:441－445.

［8］TAO Xiongfei，ZHENG Lixin，LIU Weizhong，et al.Recursive design of high Girth(2，k)LDPC codes from(k，k)LDPC codes［J］.IEEE Communications Letters，2008，15(1):70－72.

［9］朱联祥，杨海燕.一种构造八环准循环LDLC码的搜索算法［J］.重庆邮电大学学报:自然科学版，2011，23(5):570－573.

［10］LU J，MOURA J M F.Structured LDPC codes for high－density recording:large Girth and low error floor［J］.IEEE Trans.Magnetics，2006，42(2):208－213.

［11］FAN Jun，XIAO Yang.A method of counting the number of cycles in LDPC codes［C］//Proc.8th International Conference on Signal Processing.Beijing:IEEE Press，2006:156－163.

［12］SHANNON C E.Communication in the presence of noise［J］.Proceedings of the IEEE Publication，1984，72(9):1192－1201.