分布式空频码自适应联合编译码方案性能研究

刘 伟，李 宇

(河南科技大学电子信息工程学院，河南洛阳 471023)

MIMO技术和OFDM技术的结合为无线通信提供了新的发展方向［1］。但是由于在小体积的移动设备上安装多根天线并确保各天线相互独立是很难实现的，人们提出了协作通信系统，若干地理位置分散的单天线移动终端通过相互协作实现虚拟的MIMO系统［2－4］。将空时编码应用于OFDM系统中，空频编码便由此诞生。在各种空时编码技术中，线性分散码(LDC)具有突出的优势，它能够在分集增益和复用增益之间进行折中［5－6］。在各种检测算法中，最大似然检测(ML)是最优算法，但其译码复杂度随着天线数目和调制阶数的增加成指数增长，线性检测算法如ZF、MMSE等，虽然复杂度较低但性能与ML相比有较大差距［7］。信道矩阵条件数对信道容量有重要的影响，文献［8］表明，次优检测算法与ML算法性能差异的根源在于条件数的影响。文中针对分布式线性分散码空频编码系统，充分利用信道条件数，提出了一种新的自适应编码和自适应译码联合的方案。中继节点根据信道状况自适应选择分散矩阵和调制方式，接收端根据设定的信道条件数阈值自适应选择译码算法，并在COST207典型城市信道模型下进行了MATLAB仿真。仿真结果表明文中所提算法能够有效改善系统的性能。

1 系统模型

分布式空频编码系统模型如图1所示，系统由1个源节点、M个中继节点和1个接收节点组成，其中源节点和中继节点为单天线，接收节点为多天线，接收天线数目为N，OFDM子载波数为K。源节点将调制后的数据发送给各中继节点，中继节点进行空频编码并采用OFDM调制发射出去，接收端进行OFDM解调并译码得到发送信息。

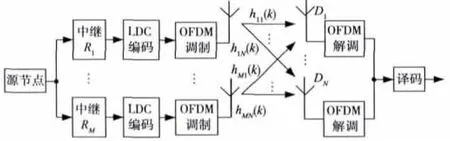
图1 空频编码系统模型

当CP的长度大于多径时延，系统能够完全消除符号间干扰(ISI)和载波间干扰(ICI)。接收端去除CP并进行FFT计算后，可得第k个子载波接收符号的表达式为

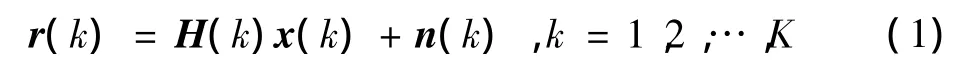
式中:x(k)=［x1(k)，x2(k)，…，(k)］T是各中继节点第k个子载波发送符号矢量;n(k)=［n1(k)，n2(k)，…，(k)］T为高斯白噪声;是频域信道矩阵。假设系统完全同步，源节点、中继节点以及接收端能够获得理想的信道信息，则系统可以看作一个虚拟的M×N的MIMO系统，接收端就可以采用MIMO系统的检测算法进行译码。

2 线性分散码(LDC)

式中:Q为每组编码要发送的信息符号数，即S=［s1，s2，…，sQ］T;αq，βq是第q个发送符号的实部和虚部。LDC的设计关键是一组符号的持续时间T、信息符号数目Q以及分散矩阵Aq和Bq的确定。通过参数的设定，LDC能够在分集增益和复用增益之间进行折中。具体的设计过程在文献［5－6］中有详细介绍。

在协作通信空频编码系统中，由于编码是在空域和频域进行的，第一阶段的发送时间是Q个符号周期，第二阶段符号的持续时间体现在占用子载波的个数，设为N。这里重新定义系统的发送速率为

线性分散码［5］定义为

式中:r为信号的调制阶数(如r－QAM，r－PSK)。

3 自适应空频编码和译码方案

信道矩阵H的条件数定义为

式中:λmax和λmin分别为信道矩阵H的最大和最小奇异值。矩阵条件数反应了方程组的病态程度，在MIMO系统中有着重要的作用。文献［8］表明，次优检测算法与ML算法性能差异的根本原因在于条件数的影响。条件数描述了多维星座被扭曲的程度［8－9］，条件数越大扭曲程度越高，噪声对发射信号的影响也就越大，信号的译码也就变的更为困难。信道矩阵条件数越趋向于1，信道容量就越大，此时线性检测也能够获得和最大似然检测相同的分集阶数［8］。根据信道状况和信道条件数，设计如下自适应编码和译码方案:

1)中继节点自适应选择编码方案

信噪比是衡量信道状态的关键指标之一，不同的线性分散码在相同信噪比下会有不同的性能，因此可以根据当前信道的信噪比选择不同的线性分散码来提高系统的性能。

2)接收端自适应选择译码方案

条件数可以由CH=‖H‖*‖H－1‖计算得到，根据CH的大小，设置阈值θ，当CH＜θ时采用MMSE译码方法;反之采用ML译码方法。CH越接近于1，线性检测的性能越接近于最大似然检测。由于线性检测的复杂度要低于ML译码，可以通过调节θ的大小来权衡译码复杂度与系统误码率性能。

4 性能仿真

中继节点数目为2，接收端天线数目为2，源节点到中继节点的信道为平坦瑞利衰落，中继节点到目的节点的信道采用6径COST207典型城市信道模型。中继节点以及目的节点能获得理想的信道信息。OFDM子载波个数为256，带宽10 MHz，每帧40 bit循环前缀。信道的多径衰落和多径延迟为

图2在文中所提分布式空频编码系统中仿真了T=2，Q=2，16QAM 和T=2，Q=4，8PSK 两种线性分散码的误码率性能，采用ML译码。这两种编码方案码率相同，从图中可以看出，在不同的信噪比区间，两种编码的误码率性能并不一样。因此有必要根据不同的信道状态使用不同的编码方式和调制方式来改善系统的性能。

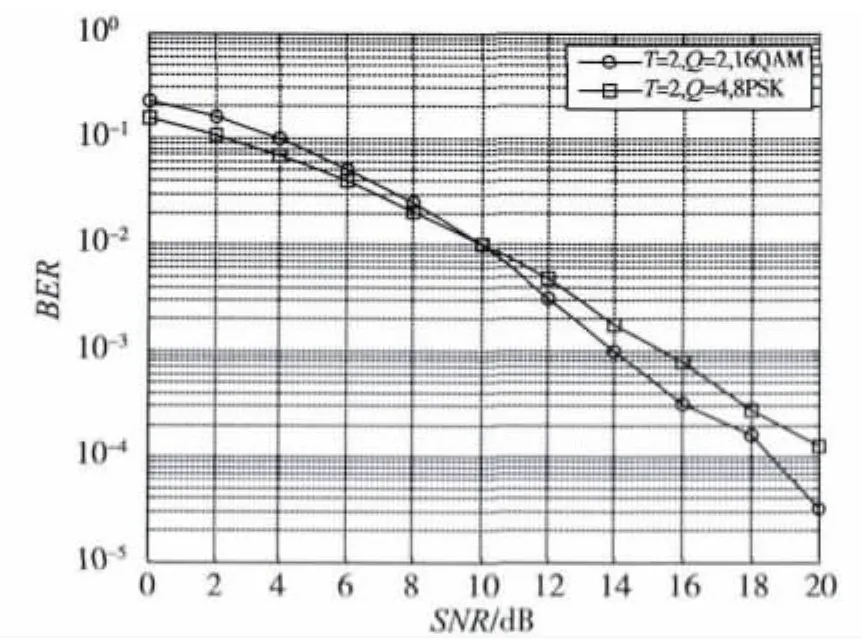
图2 码率相同，分散矩阵不同的线性分散码性能对比

图3仿真了文中所提自适应译码方案，线性分散码使用T=2，Q=4，8PSK，译码条件数阈值 θ分别为3，5和7。仿真结果表明，阈值θ越小，译码性能越好，但随着阈值的减小，会更大可能地使用ML译码，译码复杂度也相应升高。因此可以通过调整阈值θ的大小，来调节译码复杂度。

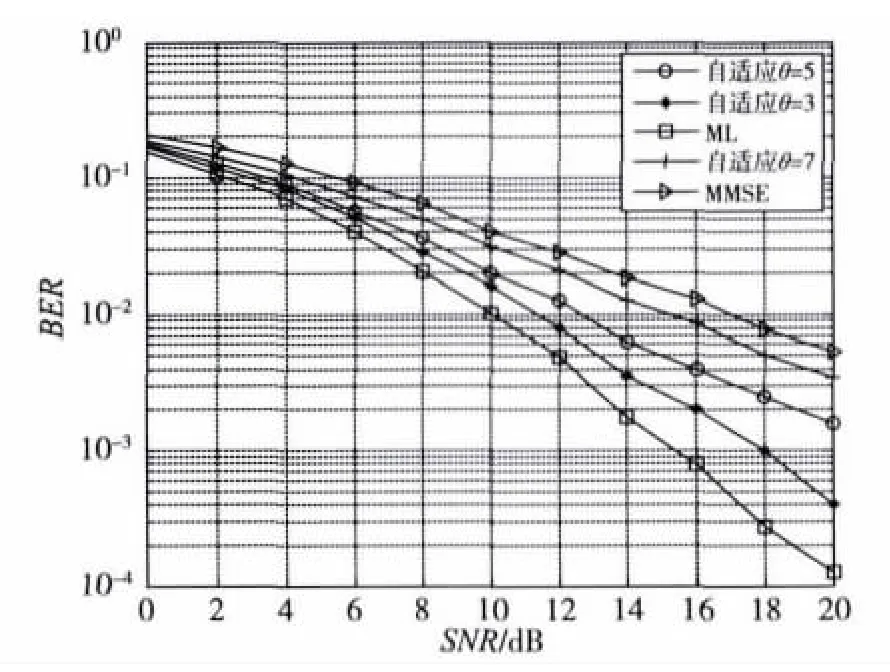
图3 自适应译码算法性能T=2，Q=4，8PSK

图4将自适应编码和译码结合在一起进行了仿真，译码条件数阈值θ=3，候选编码选用图2中所用编码，自适应信噪比阈值设为10 dB。可以发现，加入自适应编码后系统的性能进一步得到了提高，自适应编码在信道状况不好时会选取低阶调制，在一定程度上也降低了译码复杂度。自适应编码和译码相互配合，能够最大可能地提高系统的误码率性能，降低译码复杂度。

图4 自适应编码和译码算法性能，θ=3

5 小结

文中针对分布式线性分散码空频编码系统，充分利用信道条件数，提出了一种新的自适应编码和自适应译码联合的方案。中继节点根据信道状况自适应选择分散矩阵和调制方式，接收端根据设定的信道条件数阈值自适应选择译码算法，并在COST207典型城市信道模型下进行了MATLAB仿真。仿真结果表明文中所提算法能够有效改善系统的性能。

:

［1］周恩，张光，吕召彪，等.下一代宽带无线通信OFDM与MIMO技术［M］.北京:人民邮电出版社，2008.

［2］ZHANG Y，CHEN H H，GUIZANI M.Cooperative wireless communications［M］.［S.l.］:CRC Press，2009.

［3］DOHLER M，LI Y H.Cooperative communications:hardware，channel＆ PHY［M］.［S.l.］:John Wiley and Sons Press，2010.

［4］肖小潮，郑宝玉，许晓荣.协作MIMO中分布式空时编码技术的研究［J］.信号处理，2011，27(3):340－345.

［5］HASSIBI B，HOCHWALD B M.High－rate codes that are linear in space and time［J］.IEEE Trans.Information Theory，2002，48(7):1804－1825.

［6］GOHARY R H，DAVIDSON T N.Design of linear dispersion codes:asymptotic guidelines and their implementation［J］.IEEE Trans.Wireless Communications，2005，4(6):2892－2906.

［7］项玉玲.多天线系统中信号发射方案与检测技术研究［D］.成都:电子科技大学，2008.

［8］MAURER J，MATZ G，SEETHALER D.Low－complexity and full－diversity MIMO detection based on condition number thresholding［C］//Proc.IEEE International Conference on Acoustics，Speech and Signal Processing.Honolulu，HI:IEEE Press，2007:61－64.

［9］MA Xiaoli，ZHANG Wei.Fundamental limits of linear equalizers:diversity，capacity，and complexity［J］.IEEE Trans.Information Theory，2008，54(8):3442－3456.