煤矿北京54和西安80平面坐标最优转换模型研究

2014-09-18刘作军李崇贵朱学军

地下水 2014年4期

刘作军，李崇贵，朱学军

(1.四川省川煤矿山勘测设计有限责任公司，四川成都610031;2.西安科技大学，陕西西安710054)

1 常用转换模型

两套坐标系平面坐标之间常用的转换模型包括赫尔默特相似变换、仿射变换、双线性变换、二次曲面变换和考虑高程起伏的仿射变换等［3，7］。不同模型所包含待求参数的个数、模型的转换精度和对控制点数量及分布的要求不尽相同。最优模型应该是转换精度最高、所需公共点数量最少、对控制点空间位置分布要求不高的模型。

1.1 赫尔默特相似变换

图1 北京54坐标系和西安80坐标系转换关系

如图1所示，设在某矿范围内，XOY为80坐标系，xoy为54坐标系，两坐标系之间的夹角为θ，两坐标系原点之间的偏差为(ΔX0，ΔY0)，设P为矿区任一控制点，其对应的54坐标和 80 坐标分别为(xp，yp)，(Xp，Yp)。

可以推证，赫尔模特相似变换用于两套坐标系平面坐标之间的转换关系为

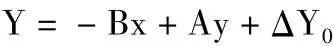
当利用个公共点解算(1)式中的待求参数时，可得如下观测方程

待定参数的最小二乘解为

求解赫尔模特相似变换模型，至少需要2个控制点。

1.2 仿射变换

仿射变换也称为6参数变换，其变换模型为

黑石集团下属的管道运营商EagleClaw中游公司宣布，将以9.5亿美元的现金收购美国卡普罗克中游控股公司（Caprock Midstream Holdings），交易预计年内完成。卡普罗克拥有4套天然气处理设施，其中2套在建，完工后的总处理能力将达到5.4亿立方英尺/日。此外，该公司还运营总计300英里长的管道储运设施，目前主要为特拉华盆地的勘探开发企业提供油气以及水的加工和处理服务。收购卡普罗克将有助于EagleClaw成为特拉华盆地重要的油气处理和管道储运商。

式中，(X，Y)和(x，y)分别为80坐标系和54坐标系中的坐标点对，a1、a2、a3、b1、b2、b3为待求参数。其中，a1、b2分别确定点(x，y)在80坐标系中X、Y方向上的缩放尺度，a2、b1确定旋转尺度，a3、b3确定在X、Y方向上的平移量。可根据矿区n个公共点，建立仿射变换模型的纵横坐标转换方程。求解仿射变换模型，至少需要3个控制点。

1.3 考虑高程的仿射变换

若在(5)式的模型中，考虑控制点高程的影响，则可得改进的仿射变换模型为

该模型的求解，至少需要4个公共点。

1.4 双线性变换

为探讨矿区54坐标系和80坐标系在不同位置处转换可能存在的异常差异，可以考虑采用以下双线性变换模型

该模型求解，也至少需要4个公共点。

1.5 二次曲面变换

典型的二次曲面变换模型为

求解该模型，至少需要6个公共点。

2 试验研究

为分析各种模型的坐标转换精度，控制点数量和空间位置分布对建模精度的影响规律，现选择陕西某煤矿若干地面和井下控制导线点，这些控制导线点既有54坐标，又有80坐标。各控制导线点坐标成果如表1所示。

表1中各控制点在这些控制点中，E91、E92和E93是地面四等GPS控制点，已经验证E91点存在较大点位误差。为分析各种转换模型的坐标转换精度、受控制点数量和空间位置分布的影响规律，以便研究最优转换模型，现设计以下3种建模方案:

(1)取表1中序号为奇数行的控制点建模，用偶数行的控制点检验所建模型的预报精度;

(2)取表1中序号为1～20的点建模，用其余点检验建模精度;

(3)取表1中序号为20～39的点建模，用其余点检验建模精度。

分别就上述各方案建立转换模型，计算各模型的纵横坐标残差和对未参与建模控制点的纵横坐标预报偏差，残差和预报偏差中误差对应表2中各种模型的第一行和第二行值。

分析可得，模型1、2和4的残差和预报偏差相近，模型5效果最差。因建模所用控制点E91存在较大误差，该模型在纵轴方向的残差显著增大，而模型5和3在横轴方向的残差也比其模型略大。综合考虑残差和预报偏差，模型2表现最佳。方案1建模所用控制点数量较多，且空间位置分布相对均匀，说明模型5受已知点精度影响的敏感性较大，模型2受其影响则很小。

分析当建模用控制点集中分布在导线的一端时，各种模型的残差相对较小，且比较稳定，只有模型1相对其它模型略显偏大。就预报偏差而言，模型1效果最好，其次是模型2和模型4。虽然模型5的残差较小，但预报偏差却很大。当预报控制点离开建模用控制点越远，预报偏差就越大。此方案说明，若建模用控制点分布集中，各种模型受建模用控制点存在较大误差的影响不敏感，模型残差虽然较小，但预报偏差却可能很大，残差已经不能反映建模精度。建模控制点越集中，所建模型适用的空间范围就越小。

分析当建模用控制点集中在导线的另一端，且控制点没有较大误差时，各种模型的纵横坐标残差均很小。但就预报偏差而言，模型5效果还是最差，其次是模型3。预报效果最好的是模型2和模型4。伴随预报控制点逐步远离建模用控制点，预报偏差将逐渐增大，当被预报点本身有较大误差时，预报值偏差也非常明显。