基于信道特征量化的自适应密钥生成方案设计

戴峤，金梁，黄开枝

(国家数字交换系统工程技术研究中心，河南 郑州 450002)

1 引言

与有线通信相比，无线通信在一定范围内不受地理环境的限制，覆盖范围更大，使用更加灵活自由，因此无线通信的应用日益普及。伴随着无线通信应用领域的拓展，对其安全性的要求也越来越高。与有线信道不同，无线信道具有开放性和广播性，如果使用与有线通信相同的加密方法，密钥的分发十分困难，所以需要寻找一种适合无线信道的加密方法。

Ahlswede和Csiszar[1]，以及Maurer[2]首先提出了合法用户利用共享随机信息生成密钥的思想。之后，Hershey[3]等提出在时分双工的通信系统中，利用无线信道的互易性实现合法用户对物理层信道特征的共享，并从中提取密钥，达到密钥分发的目的；同时利用信道特征的随机性和独有性，保证密钥的安全性。在之后的十几年中，针对不同信道特征的特点，众多实际的密钥生成方案被提出[4~10]，这些方法至少包含2个步骤：信道特征量化与信息协商，分别用于生成保密序列及纠正其中的不一致位。

研究表明量化与协商算法对密钥强度与系统有效性的影响显著[11,12]。量化算法中过高的量化精度或不适合的量化区间会增大噪声对量化结果的影响，导致生成的保密序列不一致率过高，不仅无法用于加密，还需要耗费大量资源进行信息协商，降低系统的有效性；若为了保证保密序列的一致率，对信道特征采用较低的量化精度，又会导致生成密钥熵率低，易被破解，降低通信的安全性。同时，由于不同协商方法对不一致位的处理方法不同，导致协商之后的密钥性能不同。但是由于密钥速率与量化及协商算法之间不存在简单的函数关系，所以现有方法均选择了固定的量化及协商算法，导致系统不能自适应信道信噪比的变化，无法同时满足密钥强度及系统有效性的需要。

针对这一问题，本文通过优化信道特征的量化算法及协商方案，提出了一种基于信道特征量化的自适应密钥生成方案。由于实际的密钥速率曲线复杂，本文首先提出了密钥速率的上界函数曲线，该曲线假设在量化精度小于密钥速率上限时不存在量化不一致的情况，是实际密钥速率的上界函数，并据此提出了自适应量化算法；然后通过消除量化噪声，在减小量化不一致率的同时提高密钥速率，使实际曲线与上界函数曲线更加接近；接着利用该上界函数曲线代替实际曲线对量化精度进行分析，指出当量化精度大于密钥速率上限时，不一致率将迅速上升导致密钥速率不再提高，所以选用密钥速率上限作为量化精度，以同时保证较低的不一致率与较高的密钥速率。在该算法的基础上，通过分析不同协商方案生成密钥的熵率，得到了依据信道噪声阈值进行协商方案选择的方法。最后，利用上述关键算法得到自适应的密钥生成方案。仿真结果表明，与现有方法相比，在量化精度较低时，利用量化噪声消除算法可以将密钥熵率提高1 bit/时隙。在任意信道噪声条件下，利用本文方案可实现不低于理论上限0.3 bit/时隙的密钥熵率以及95%以上的一致率，同时保证密钥强度及系统有效性。

2 系统模型及问题描述

2.1 基于信道特征量化的密钥生成模型

基于信道特征提取的密钥生成模型如图1所示。Alice为发送者，Bob为合法接收者，Eve为被动窃听者，三者均为单天线。其中，Alice与Bob之间的信道称为主信道，选取主信道的相位响应0u作为生成密钥的随机变量。假设信道为块衰落信道，则0u在一个时隙内不变，在不同时隙取值独立。

Alice与Bob通过在同一时隙内测量对方发送的导频信号对0u进行估计，得到Au和Bu

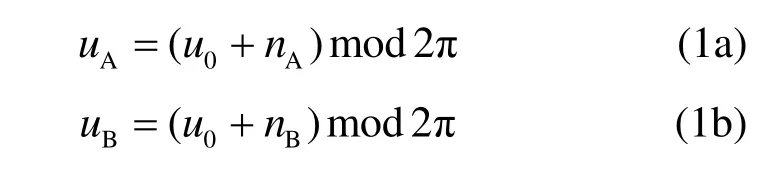
其中，uA与uB为零均值复高斯噪声。令ΔB=uA- uB为Alice与Bob对 u0的测量误差，结合式(1)可得 ΔB= uA- uB。实验表明，信道具有短时互易性[4~8]， uA与 uB的相关性非常大，且 uA与 uB方差相等，假设为σ2，则ΔB~ N(0,2σ2) 。同时由于无线信道的独有性，当Eve与Bob相距超过通信波长的一半时，信道相位响应的相关性就会降到 0.2以下[9]，所以认为 uA与 uB是安全的。

如图1所示，Alice与Bob通过量化 uA和 uB得到保密序列 vA与 vB。其中， QL(⋅)为量化函数，量化级数为L。 Pe为 vA与 vB不一致的概率，当 Pe≠0时，为了保证最终密钥的一致性，合法用户需要通过公共信道发送协商信息协商C，使保密序列达成一致。假定公共信道是无噪的，且C可被Eve得到。

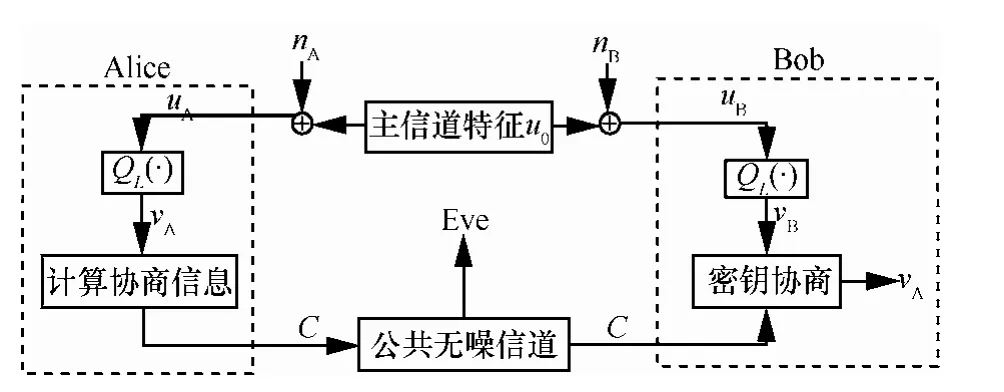
图1 基于无线信道特征的密钥生成模型

协商方案有纠错[12]与检错[4,6]2种。纠错方案是指Alice将可实现纠错的协商信息发送给Bob，Bob利用此信息纠正保密序列中的不一致位；密钥检错方案是指Alice将可实现检错的信息发送给Bob，后者根据收到的信息判断自己的保密序列是否与Alice一致，若一致则利用其生成密钥K，否则就丢弃。

2.2 问题描述

密钥生成的关键是如何利用Au和Bu生成一致的密钥K，下面从生成密钥的强度以及系统的有效性2个方面对密钥生成方案进行分析。

在保密通信中使用密钥熵率对密钥的强度进行衡量。密钥熵率定义为在K安全的条件下合法用户每时隙生成K的平均熵值。熵的物理概念为不确定性，当量化精度较低时，量化结果取值单一、不确定性较小，导致利用其生成的密钥空间小、强度差。所以需要通过提高量化精度来扩大密钥空间，达到提高密钥强度的目的。

虽然通过提高信道特征的量化精度可以提高生成密钥的强度，但是过高的量化精度会导致噪声的影响增大，使不同用户量化结果的不一致率增加。而较高的不一致率导致需要多轮协商才能完全去除不一致比特，消耗资源过多。同时由于协商会暴露保密序列的信息，所以当保密序列的不一致率大于11%时，利用现有信息协商方法将无法获得一致的密钥。所以应该在保证双方量化一致率较高的前提下提高量化精度，从而保证系统的有效性。

现有文献也发现了存在于密钥强度及系统有效性之间的权衡问题[11]，但是由于密钥速率、不一致率与量化及协商算法的关系复杂，所以并未出现有效的解决方法。针对这一问题，本文提出了密钥速率上界函数的概念，并在此基础上提出了自适应量化算法。该上界函数由不同量化精度下密钥速率的上界构成，物理意义为当量化精度小于密钥速率上限时不存在量化结果不一致的情况。所以量化结果的不一致率越小，密钥速率就越接近该上界函数。自适应量化算法通过消除量化噪声来提高密钥速率，使上界函数更加接近实际的密钥速率。在此基础上通过分析上界函数曲线，发现当量化精度超过密钥速率上限时，保密序列的不一致率迅速上升而密钥速率基本不变，所以提出将密钥速率上限作为量化精度。接着通过比较不同信噪比条件下2种协商方案在该算法基础上生成密钥的熵率，给出了信息协商方案的选择方法。

最后，本文在上述算法的基础上给出了基于信道特征量化的自适应密钥生成方案，达到同时保证系统强度与有效性的目的。

3 关键算法设计与分析

本节给出了基于信道特征量化的自适应密钥生成方案中的2个关键算法：自适应量化算法以及协商方案选择方法。其中，自适应量化算法在密钥速率上界函数的基础上得到，包含量化噪声消除以及量化精度优化2个子算法。

3.1 密钥速率上界函数曲线

无线通信信道的相位响应与电磁波的传播路程有关，因此通信双方只要是处在移动中，0u就在不停地变化，且服从[0,2π)上的均匀分布。而当信道中障碍物较多时，即使通信双方不移动，信道的相位响应也为均匀分布。同时因为An、Bn与0u独立，所以Au 与Bu服从[0,2π)上的均匀分布，采用均匀量化器对Au与Bu进行量化。

纠错方案下的密钥熵率cR等于密钥速率[1,2,13]

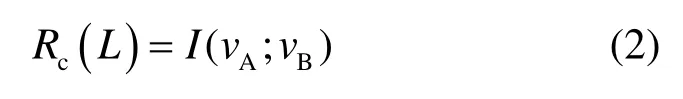
当量化精度趋于无穷大时，得到密钥速率的上确界R为[14]

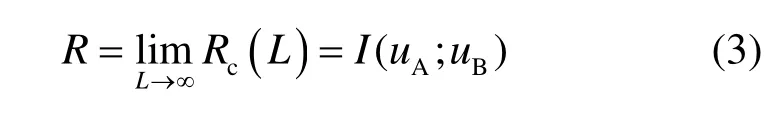
而当量化精度较小时有

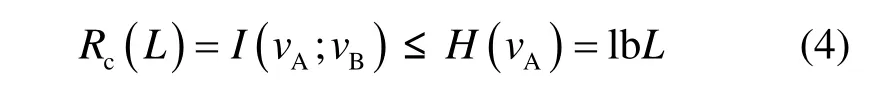
其中，L为量化精度。据此给出密钥速率的上界函数为

对任意L，都有 Rc'（L）≥ Rc（L）。该曲线的物理意义为当 lb L ＜ I（ uA; uB）时，不存在量化不一致的情况。实际上，当L接近 I（ uA; uB）时，Pe逐渐增大，I（ vA; vB）≤lbL，导致式（5）与实际曲线出现误差。通过采用3.2节中的量化噪声消除算法可使 Pe大大减小，进而减小该误差，具体的误差大小将在 3.3节中说明。

检错方案的密钥熵率为

其中，1 - Pe为Alice与Bob对信道特征量化结果一致的概率，即密钥可用的概率。 Rd满足

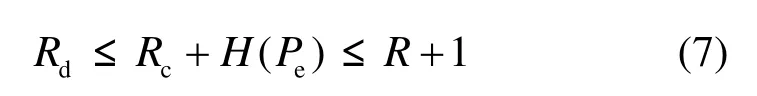
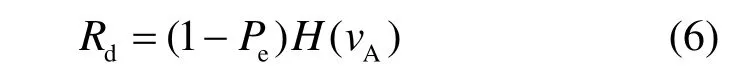
证明见附录 A。从式（6）可以看出：当量化精度较低时，由于 Pe较小，所以 Rd十分接近H（ vA） ；又因为 Pe≥ 0 ，所以有 Rd≤H（ vA） 。同时根据式（7）可知， Rd的上限也受到R的限制。所以利用式（5）得到的自适应量化算法同样适用于检错策略。不同之处在于 Pe较大时 Rd接近0，采用检错方案将会造成密钥生成的中断，依据自适应量化算法可以避免这种情况出现。

Rd定义为信息论安全条件下密钥熵率的最大值，之所以会出现 Rd大于R的情况，是因为检错方案的安全性还来源于计算安全。实际中常采用散列函数值作为检错信息，假定当窃听者的计算能力有限时，无法通过散列函数值 VA= h ash(vA)得到vA，所以广播 VA不会影响 vA的安全性。由于 vA的安全性不仅来源于信息论安全，还包含计算安全，所以利用检错方案得到的密钥熵率可能大于密钥速率。

3.2 自适应量化算法

Alice对Au量化得到Av，产生量化噪声Qn，则有关系

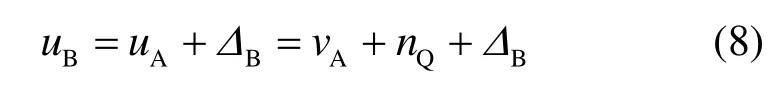
从式（8）中可以看出 nQ会导致 uB与 vA的误差增大，使 Pe上升。所以有必要通过消除 nQ来减小Pe。容易证明，均匀分布的量化结果与量化噪声相互独立，所以公开 nQ不会影响 vA的安全性。

所以，当Alice量化完成之后，可以将 nQ公开地发送给Bob。Bob对 uB平移 nQ得到 uB'，再进行量化则可消除量化噪声的影响。

Bob对 uB'量化得到 vB，则量化结果的不一致率为

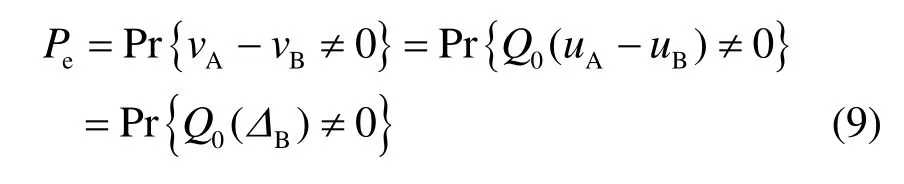
同时可知

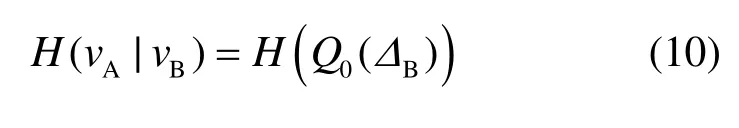
根据高斯分布，当均值与量化区间的中点重合时，落在其他量化区间的概率最小。所以经过量化噪声消除之后， Pe与 H ( vA|vB)均取到最小值，系统有效性最高。同时，根据

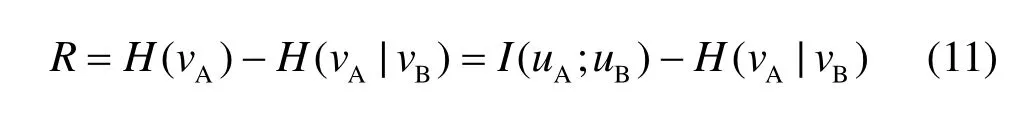
可知，此时密钥速率接近上界，所以可以保证生成密钥的强度。

经过量化噪声消除之后， Rc（L）与 Rc'（L）已十分接近。依据式（5）给出的 Rc'（L）可知，当lbL＞I（ uA; uB）时， Rc'（L）不再随L增大；且当lbL＞I（ uA; uB）时，一定有 Pe＞ 0 。这是因为

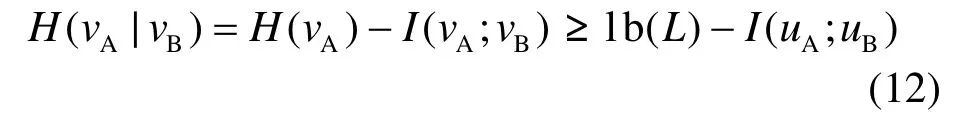
所以当 l b L ＞I( uA; uB)时，有H( vA|vB) ＞ 0 ，依据Fano不等式可知 Pe＞ 0 。为了使 Pe较小，应满足lb L ≤ I ( uA; uB)。据此得到量化精度的优化算法

其中，[]⋅表示取整。

3.3 协商方案选择方法

实际中为了保证生成密钥的强度，需要接收导频信号的信噪比足够大。所以本文对上述算法在大信噪比条件下的性能进行分析，并在此基础上给出协商方案的选择方法。

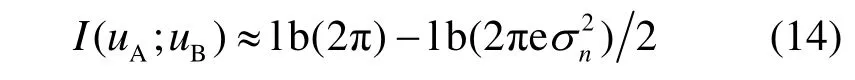
将lb L = I ( uA; uB)代入式（14）得到量化间隔根据自适应量化函数可知噪声均值位于量化区间中点，正态分布的随机变量落在均值附近4.13倍标准差区间内的概率为0.960 6，所以有 Pe=0.039 4。 Pe较小说明上界函数曲线可以较好地近似实际曲线。同时得到 H ( vA|vB)=0.278 9，代入式（2）与式（6）得到

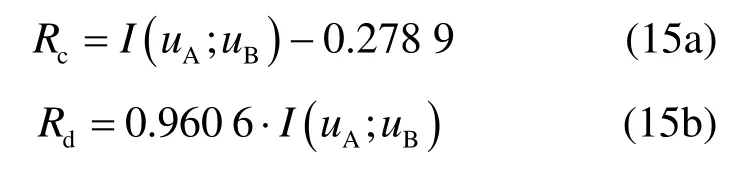
比较以上两式，得到当 I （ uA; uB）≤ 7 .07时，Rc＜Rd，否则Rd较大。将这一结果代入式（14），得到协商方案选择方法如表1所示。其中， S NR0=- 2 0lg，为接收导频信号的信噪比。表1说明在主信道信道条件较好时，应利用密钥纠错方案减少协商暴露的信息，从而提高生成密钥的强度；否则应采用检错方案保证生成密钥的一致性。所以协商时应根据 S NR0的取值自适应地选择合适的协商方案。

表1 协商方案选择方法

之所以能够得到表1的结论，是因为采用量化精度自适应选择与自适应量化函数生成密钥的不一致率不变，但是当信噪比较小时，量化精度较低，检错方案丢弃不一致密钥对性能影响较小，同时由于协商时泄露信息较少，所以与纠错方案相比性能更好；而信噪比较大时可采用较高的量化精度，丢弃不一致密钥的同时将大量一致的密钥比特丢弃，导致检错方案性能下降。

4 基于信道特征测量的自适应密钥生成方案

下面结合自适应量化算法与协商方案选择方法，给出基于信道特征测量的自适应密钥生成方案的具体步骤。

1) Alice与Bob在一个时隙内交替发送导频信号，并对接收信号进行多次测量，Alice计算接收导频信号的信噪比 S NR0。

2) Alice将 S NR0代入式（3）对生成密钥的速率进行估计，并判断该速率能否满足系统安全性的要求。

3) 若通过步骤2）判断得出生成的密钥速率较低，则通知Bob增加导频信号的发送功率，并回到步骤1）。否则根据表1确定采用的协商方案，并利用式（13）计算量化精度L，同时通过无噪公共信道将选定的协商方案以及L告知 Bob。由于 Alice与Bob接收到的噪声功率相同，所以Bob可以直接对 uB进行L级量化。

4) Alice对 uA进行L级量化得到 vA，计算nQ= uA- vA，并通过无噪公共信道发送给Bob，Bob将 uB平移 nQ得到 uB'，量化 uB'得到 vB。

5) Alice根据所选的协商方案进行信息协商。若使用检错方案，Alice利用散列函数生成校验信息VA，并将 VA发送给 Bob，Bob用相同的方式生成校验信息 VB，并与 VA进行比较。若 VA= VB说明两端对信道相位响应量化得到的保密序列相同，可用于生成密钥；否则，说明保密序列不同，通知Alice将其丢弃，并开始新一轮的量化；纠错方案协商方法与分布式信源编码类似，具体步骤可参考文献[2,3,15,16]。

需要说明的是，虽然散列函数具有较好的单向性，Eve很难根据AV推算出Av，但是AV还是会造成Av的泄露，所以应尽可能地降低量化结果的不一致率，减少协商信息的传递。

6) Alice与Bob将量化结果转换为二进制保密序列，并进行存储。

7) 当保密序列的累积长度达到密钥长度的要求（如128 bit、256 bit等）时，将保密序列组装成新的密钥，更新原有密钥。

整个过程由于窃听信道的相位响应Eu与0u独立，所以Eve无法得到量化结果，保证了密钥的安全。

5 仿真分析与比较

本节首先将密钥速率的上界函数曲线与实际曲线进行了比较，接着对比了直接量化与经过量化噪声消除之后生成密钥的性能，并对不同协商方案生成密钥的熵率进行了比较，最后对自适应量化精度选择方法的效果进行了仿真。仿真结果通过 10×104次蒙特卡洛实验得到，仿真条件如下：

1) u0在[0,2π)上均匀分布；

2) 导频信号为正弦信号， S NR0的取值范围为20 dB~60 dB；

3) 采用均匀量化函数，量化点坐标为{0,Δ,2Δ,…,(L-1)Δ}。

图2为不同信噪比条件下的密钥速率。从图中可以看出，由蒙特卡洛实验得到的实际密钥速率曲线经过量化噪声消除之后，能够较好地由上界函数曲线近似得到。

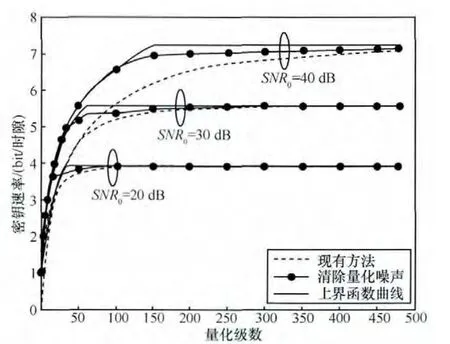
图2 密钥速率与量化级数的关系

从图2可以看出，在量化级数较低时，通过消除量化噪声可以有效降低不一致率，从而提高密钥速率。这是由于Au在量化区间上均匀分布，当Au接近区间边界时，Bu与Au落在不同量化区间的概率接近0.5，若Bob端直接对Bu量化，结果不一致的概率接近0.5；而消除量化噪声之后，Au等效为始终位于量化点上，Bu与Au落在不同量化区间的概率大大降低。

图3对检错方案与纠错方案生成的密钥熵率进行了比较。从图3中看出，量化精度较低时，由于密钥的不一致率较低，所以检错方案的平均密钥熵率要稍高于纠错方案；同时，检错方案的密钥速率与纠错方案之差又不超过1 bit/时隙，可以部分验证式（7）的结论。而当量化级数较大时，生成的保密序列不一致率较大，使用纠错方案可以对不一致位进行纠正，而使用检错方案会因较多不一致保密序列被丢弃，导致密钥熵率迅速下降。

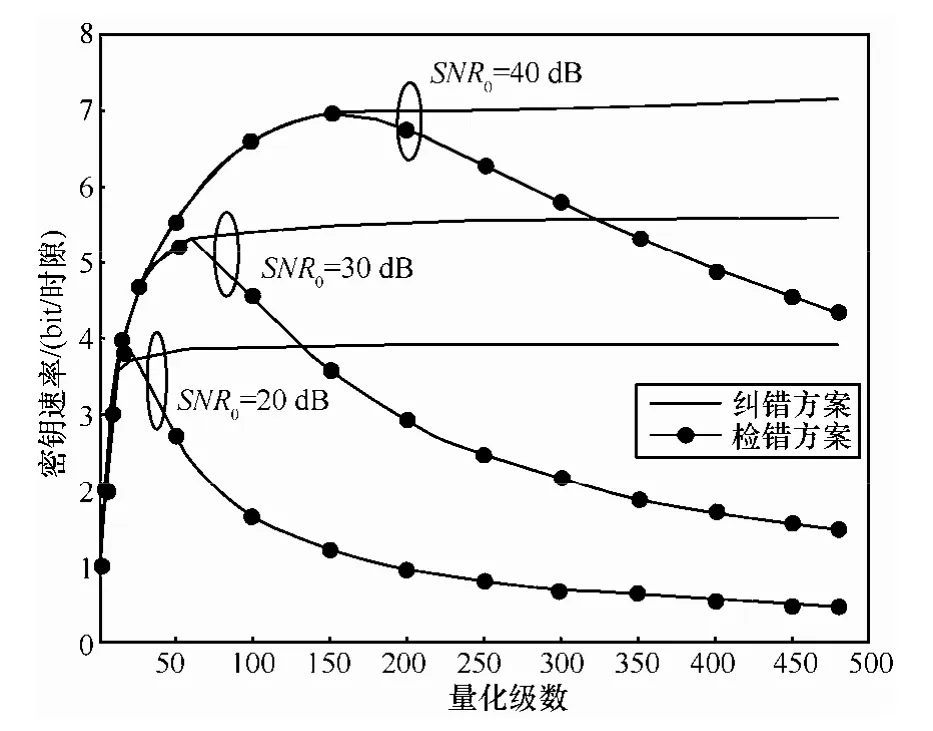
图3 纠错方案与检错方案密钥熵率比较

图 4为对信道特征采用不同量化方案在相同信道条件下的密钥性能比较图，从图 4中可以看出，使用自适应量化算法可以较好地适应信道，生成密钥的熵率接近采用 16 bit量化生成的密钥速率，同时量化结果的不一致率在 0.05之内，可以同时保证系统的安全性与有效性。而其他2种固定精度的量化方案则无法适应信道条件的变化：采用16 bit量化生成的密钥速率较高，但是不一致率也非常高，可能导致无法生成一致的密钥；而 1 bit量化的密钥速率受限于量化精度，每个时隙生成的密钥熵率不大于 1 bit，若信道变化较慢，则无法满足通信需求。

从图4（a）中可以看出，在SNR0小于40 dB时，检错方案的平均密钥速率大于纠错方案的密钥速率；而当SNR0大于40 dB时，检错方案的平均密钥速率逐渐低于纠错方案的密钥速率。所以应根据表1选择合适的协商方案。

6 结束语

通过量化信道特征得到密钥，利用信道的时变性及独有性保障通信的安全，是一种有效的物理层安全方法。如何选择信道特征的量化参数，同时保证系统的安全性与有效性是该方法的主要问题。本文首先提出了自适应量化算法：选择密钥速率上界函数曲线代替实际复杂的曲线对量化精度及一致率进行分析，同时通过消除量化噪声的影响，在保证一致率的条件下提高信道特征的量化精度。然后在该算法的基础上，通过分析不同协商方案生成密钥的熵率，得到了依据信道噪声阈值进行协商方案选择的方法。最后，利用这2种算法得到基于信道特征量化的自适应密钥生成方案，并通过仿真验证了该方案的有效性。

本文研究了如何利用相位响应生成密钥，下一步将考虑利用信道的幅度及相位响应构建的二维随机变量生成密钥，进一步提高生成密钥的强度。

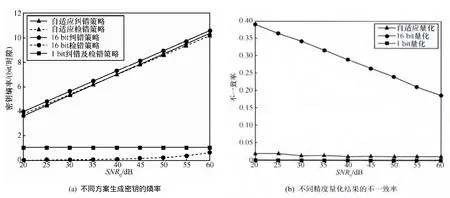
图4 不同量化方案密钥性能比较

附录A 式(7)的证明

证明 引入错误指示变量E。

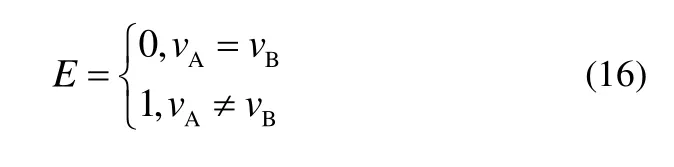
则有

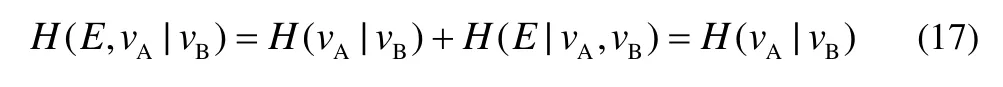
利用熵计算法则展开得到

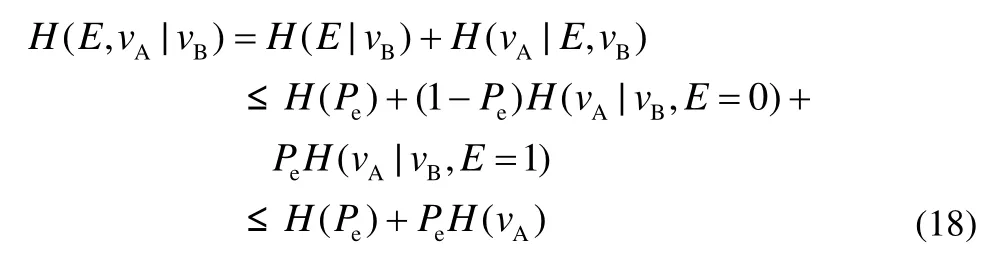
联立式（8）、式（9）可得

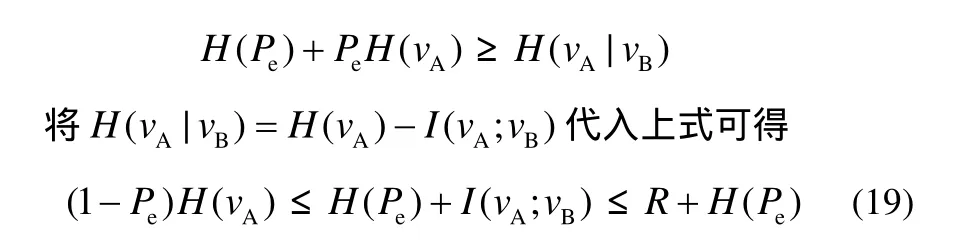
证毕。

[1] AHLSWEDE R, CSISZAR I. Common randomness in information theory and cryptography secret sharing[J]. IEEE Trans on Information Theory, 1993, 39(4):1121-1132.

[2] MAURER U M. Secret key agreement by public discussion from common information[J]. IEEE Trans on Information Theory, 1993,39(3):733-742.

[3] HERSHEY J E, HASSAN A A, YARLAGADDA R. Unconventional cryptographic keying variable management[J]. IEEE Trans on Communication, 1995, 43(1):3-6.

[4] MATHUR S, TRAPPER W, MANDAYAM N, et al. Radio-telepathy:extracting a secret key from an unauthenticated wireless channel[A].Proc of the 14th ACM International Conf on Mobile Computing and Networking[C]. San Francisco, USA, 2008. 128-139.

[5] AONO T, HIGUCHI K, OHIRA T, et al. Wireless secret key generation exploiting reactance domain scalar response of multipath fading channels[J]. IEEE Trans on Antennas and Propagation, 2005,53(11): 3776-3784.

[6] JANA S, PREMNATH N S, CLARK M, et al. On the effectiveness of secret key extraction from wireless signal strength in real environments[A]. Proc of the 15th ACM Conf on Mobile Computing and Networking[C]. Beijing, China, 2009. 321-332.

[7] WILSON R, TSE D, SCHOLTZ R A. Channel identification: secret sharing using reciprocity in UWB channels[J]. IEEE Trans on Information Forensics and Security, 2007, 9(3):17-30.

[8] YE C, MATHUR S, REZNIK A, et al. Information-theoretically secret key generation for fading wireless channels[J]. IEEE Trans on Information Forensics and Security, 2010, 5(2):240-254.

[9] SASAOKA H, IWAI H. Securing Wireless Communications at the Physical Layer[M]. Springer Publishing Company, 2010. 261-280.

[10] HAMIDA S, PIERROT J, CASTELLUCCIA C. An adaptive quantization algorithm for secret key generation using radio channel measurement[A]. The 3rd International Conf on New Technologies,Mobility and Security (NTMS)IEEE[C]. Cairo, Egypt, 2009. 1-5.

[11] YE C, REZNIK A, SHAH Y. Extracting secrecy from jointly gaussian random variables[A]. ISIT2006[C]. Seattle, 2006. 2593-2597.

[12] WANG S H, REN K. Fast and scalable secret key generation exploiting channel phase randomness in wireless networks[A].INFOCOM, 2011 Proceedings IEEE[C]. Shanghai, China, 2011.

[13] 1M4A22U-1R4E3R0 .U M, WOLF S. Information-theoretic key agreement: from weak to strong secrecy for free[A]. Advances in Cryptology-EUROCRYPT 2000[C]. Bruges, 2000.351-368.

[14] GAMAL A E, KIM Y. Network Information Theory[M]. Cambridge:Cambridge University Press, 2011.

[15] BRASSARD G, SALVAIL L. Secret-key reconciliation by public discussion[A]. Advances in Cryptology-EUROCRYPT’93[C]. Lofthus,1994. 765:410-423.

[16] YE C, NARAYAN P. Secret key and private key constructions for simple multiterminal source models[J]. IEEE Trans on Information Theory, 2012, 58(2):639-651.