Bloch空间上的积分算子的有界性和紧性*

周 林,曹成堂

(连云港广播电视大学 建筑工程系,江苏 连云港 222006)

0 引言

本文将要讨论的算子如下:

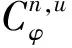
1 预备引理

引理1[5]设f∈B,那么对于任意正整数n,

‖f‖B≅∑|f(j)(0)|+

引理2[5]在B0中的一个闭子集K是紧的充要条件是K是有界的且满足

由Montel定理及紧算子定义,可以得出下面的引理.

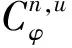
2 主要定理及证明

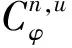
(1)

证明首先假设(1)成立,那么对于任意f∈B,由引理1可得

(1-|z|2)|u(z)f(n)(φ(z))|≤

C‖

(2)

所以

C<∞.

(3)

(4)

又因为

浙江力普在精制棉制备纤维素粉碎加工技术领域更是一枝独秀———“医药辅料纤维素醚专用高效剪切粉碎机的研究和产业化项目”“GWM-730纤维素高效剪切磨开发”相继被列入省市科技项目；高效纤维素剪切粉碎机、短纤维粉碎机均已获得国家专利。为我国纤维素粉体行业提供了一种技术国际领先的超细纤维粉碎设备。

C<∞.

由上式以及(3),(4)可得(1)成立.

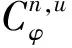
(5)

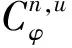
(6)

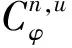
(7)

由(6)以及(7)可知,当i>i0时,有

下证‖φ‖∞=1的情况.令(zi)i∈∈D是使得|φ(zi)|→1,i→∞的点列.

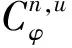
(8)

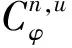
(1-|z|2)|u(z)p(n)(φ(z))|≤

(1-|z|2)|u(z)|‖p(n)(φ(z))‖B.

(9)

证明首先假设(9)成立.在(2)中对‖f‖B≤1的f取上确界,且让|z|→1,可得

(10)

由(8)成立可得,∃δ∈(0,1),当δ<|z|<1时,

(1-|z|2)|u(z)|≤ε(1-r2)n.

(11)

由(10)可得,当δ<|z|<1,r<|φ(z)|<1时,

(12)

由(11)可得,当δ<|z|<1,|φ(z)|≤r时,

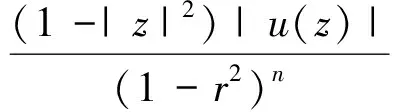
(13)

由(12)以及(13)可得(9)成立.

参考文献:

[1] ZHAO Ruhan. Composition operators from Bloch type spaces to Hardy and Besov spaces[J]. Journal of Mathematics Analysis and Applications, 1999, 233(2): 749-766.

[2] ZHU Kehe. Bloch type spaces of analytic functions[J]. Rocky Mountain Journal of Mathematics, 1993, 23(3): 1143-1177.

[3] STEVIC S. On an integral operator from the Zygmund space to the Bloch-type space on the unit ball[J]. Bulletin des Sciences Mathematiques, 2010, 134(4): 329-339.

[4] STEVIC S. On an integral operator between Bloch-type spaces on the unit ball[J]. Glasgow Mathematical Journal, 2009, 51(2): 275-287.

[5] STEVIC S. Composition by followed by differentiation fromH∞and Bloch spaces to nth weight-type spaces on the unit disk[J]. Applied Mathematics and Computation, 2010, 216(12): 3450-3458.

[6] YU Yanyan, LIU Yongmin. The product of differentiation and multiplication operator from the mixed-norm to the Bloch-type space[J]. Acta Mathematics Science Series A, 2012, 32(1): 103-122.

[7] LI Songxiao, STEVI’C S. Products of Volterra type operator and composition operator fromH∞and Bloch spaces to Zygmund spaces[J]. Journal of Mathematics Analysis and Application, 2008, 345: 40-52.