基于区间数理论的基坑周边建筑物风险模糊评判*
2014-09-17吴朝阳吴红华李正农赖华勇
吴朝阳,吴红华,李正农†,赖华勇
(1.湖南大学 土木工程学院,湖南 长沙 410082; 2. 国网江西省电力公司经济技术研究院,江西 南昌 330043)
基坑工程可能引起地层沉降、周边建筑物倾斜、开裂等,进而造成建筑物的破坏,因此对周边建筑进行风险评估和控制已逐渐成为基坑工程的关键问题之一.影响周边建筑安全的因素有很多,且机理复杂,获取相应评价指标的方法也有较大差别[1],因此很难全面评判其破坏风险.许多行业针对独立的评价指标建立了本行业的评价标准,如沉降值[2-3]、角变量[4]、裂缝[5]、倾斜度[6]等,但存在一些问题:忽略了建筑在基坑开挖前已存在的损伤状况[1];由于理论的局限性、勘测误差等原因,导致评价指标存在不确定性和随机性;一些指标不能被量化描述,只能根据专家经验粗略地评价风险;部分研究引入模糊理论来避免评判工作,如文献[7],但采用的模糊隶属函数和权重分配方案不符合基坑周边建筑风险的特点.
因此,本文以长沙某地铁车站基坑对周边大刚度建筑[8]的风险评判为例,首先,将建筑破坏风险分为4个等级,提出以最大沉降值和倾斜度[9]、损伤系数[10]为风险评价指标;其中,沉降值和倾斜度由数值法计算得到,除建筑损伤现状外,已考虑几乎所有的影响因素;可量化描述的“损伤系数”,则由相关规程[11]定性评价建筑损伤现状的方法插值来得到.其次,引入区间数理论[12-13],合理地描述指标的范围和分布概率,来反映其不确定性和随机性.最后,根据模糊理论[14]提出了S型可变模糊隶属函数,引入并改进超标加权法[15],对基坑周边建筑的风险进行有针对性的模糊综合评判.
1 模糊综合评判模型
1.1 有代表性的风险评价指标
建筑物的破坏往往是由多种因素的综合作用引起的,其风险评价的指标差异较大.文献[1]总结了预测多种指标的经验法流程,但大部分指标以沉降值和倾斜度为基础来推导,且求解难度大,常由于不能有效地预测而只能在施工监测中采用.
综合考虑指标应有的代表性和实用性,本文首先选用最大沉降值和倾斜度为基本评价指标,主要原因有:①在一定程度上可推导其他指标;②目前已被工程界广泛接受;③本文涉及的建筑为大刚度建筑[8],适合用沉降值和倾斜度来评价;④数值法[9]可以简便地计算出沉降值和倾斜度,且其模拟过程已能考虑除建筑损伤现状之外几乎所有的影响因素,如:地层条件、基坑方案、建筑在自重下的变形、建筑与基坑的位置关系等.
此外,本文考虑建筑在基坑开挖前的损伤状况,按规程[11]的评判标准改进文献[10]的方法,由房屋鉴定报告得到量化的“损伤系数”.最终,建立了代表性和实用性较强的模糊综合评判模型,如图1所示.
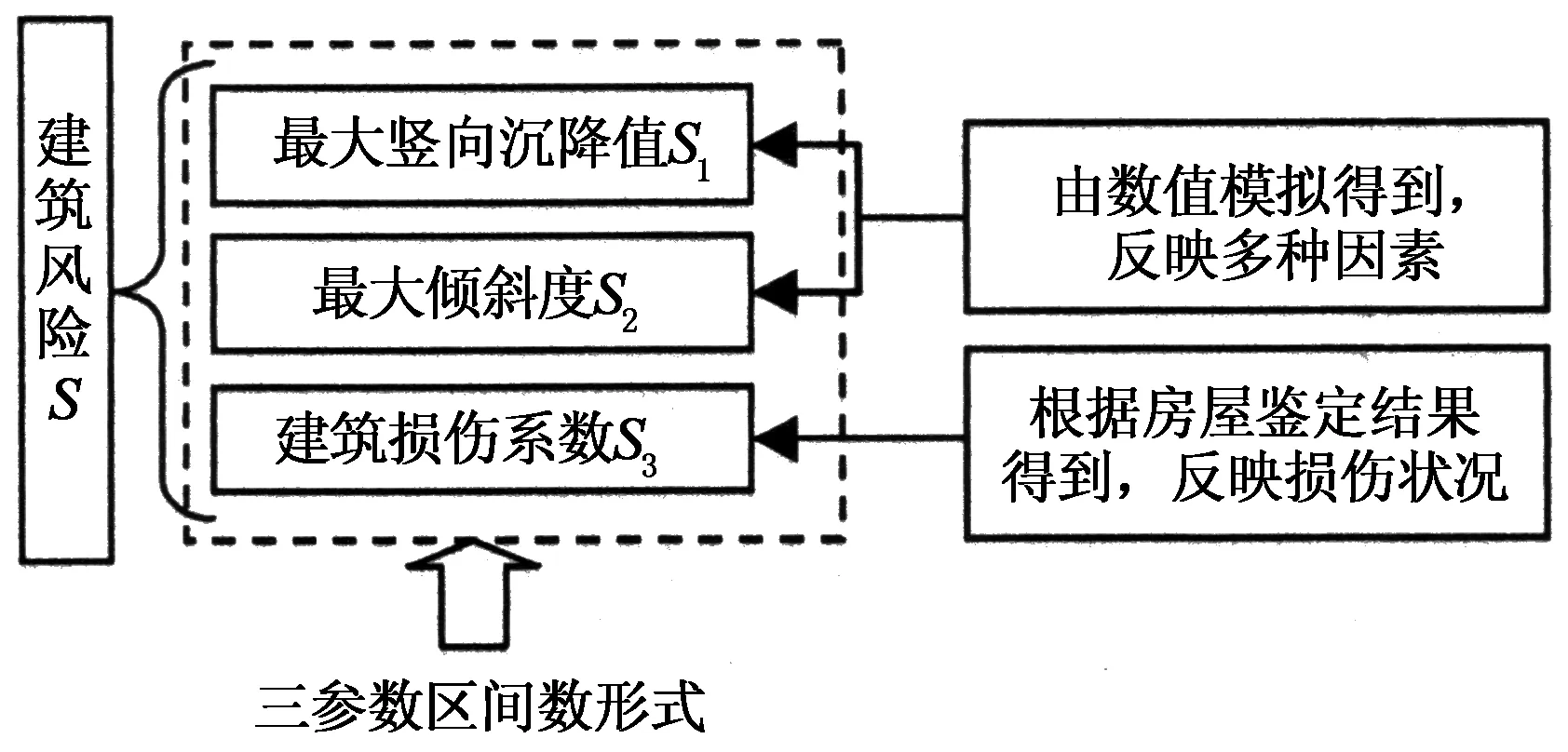
图1 模糊综合评判模型
1.2 风险的等级
对模型中的指标值,本文采用三参数区间数来描述其不确定性和随机性(见2.1节);参照文献[1,3]对沉降值、规程[11]对建筑损伤的风险分类方法,将风险分为4级:①可忽略,②一般,③较高,④很高.对每个评价指标Si,其4个风险等级区间之间由3个评价值δi1,δi2和δi3来划分.
1.3 沉降值和倾斜度
建筑沉降值的风险划分采用文献[13]的4级标准,如表1所示.此外,参考相关规程[6]取建筑在自重作用下的倾斜度限值2‰,以及基坑工程中常按此限值的60%,80%来设定预警、报警的方法,确定基坑周边建筑的倾斜度风险等级标准如表1所示.

表1 最大沉降值和最大倾斜度的风险等级
1.4 损伤系数
1.4.1 损伤系数与损伤状态
当房屋出现损伤时,可按相关规程[11]定性地评判风险.为了量化描述风险值,文献[10]提出了损伤系数的概念,定义单个构件和整个建筑的损伤系数分别为Di和D,其风险区间值如表2所示.

表2 损伤系数与损伤状态的关系
1.4.2 改进子单元的损伤系数
文献[10]先对单个构件的损伤系数Di估值,再逐步组合计算建筑的损伤系数D,但其对Di估值的方法过于主观.规程[11]的评定标准则较为客观,对子单元的每种主要承重构件的评定方法见表3.

表3 主要构件安全性等级的评定
表3对第i级的评定内容有3项,即子单元含i+1级构件的层数、每层含i+1级构件的个数、每轴或每跨含有i+1级构件的个数,可以通过计算这三项的达标程度(插值)来描述子单元(柱或墙、梁)的损伤系数e.因此,本文以多层及高层房屋为代表,定义:
当某种主要构件无任何损伤时,e=0;
当某种主要构件已被评定为第i级,即仅含i和i+1级单个构件时:
i=1,2,3.
(1)
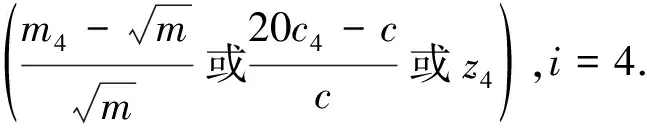
(2)
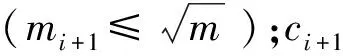
e的风险区间:a-1∈[0,k1];b-2∈[k1,k1+k2];c-3∈[k1+k2,k1+k2+k3];d-4∈[k1+k2+k3,k1+k2+k3+k4].ki为与风险级别有关的系数,可参考表2取:k0=0,k1=k2=k3=k4=0.2.计算得到的e将有3个数值,取其最小值为e-,最大值为e+,最可能值为0.5(e-+e+),即可用三参数区间数来描述(见2.1节).
1.4.3 建筑的损伤系数
规程[11]由多个子单元的鉴定结果进一步组合评定整个待鉴定单元,但其方法较为繁琐.文献[10]分析了各主要构件与房屋安全的关系,提出忽略次要构件的影响,直接由柱、墙、主梁等主要构件的损伤系数e,组合计算建筑的整体损伤系数E:
E=0.6ec/w+0.4eb.
(3)
式(3)中:ec/w为柱或墙的损伤系数,eb为主梁的损伤系数.
2 风险等级评判方法
2.1 三参数区间数原理
三参数区间数,可记为A=[a-,a△,a+]且a-≤a△≤a+,表示A的值在a-和a+之间,最可能为a△,具体定义和运算规则详见文献[12].其典型概率分布函数如图2所示,且满足式(4):
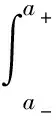
2/(a+-a-).
(4)
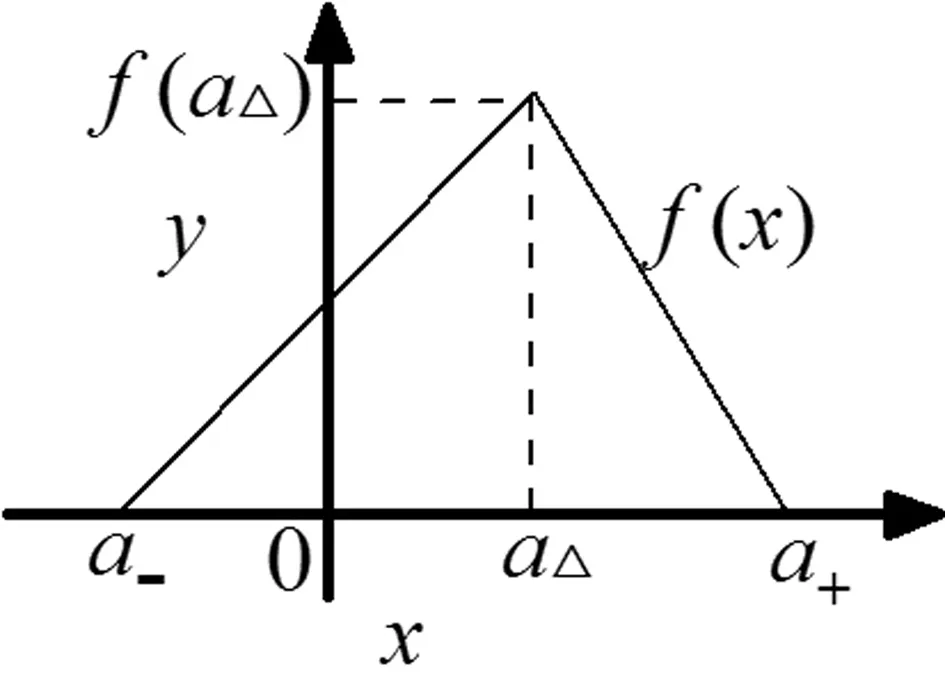
图2 三参数区间数的典型分布函数
目前,二参数区间数在地下工程风险分析中已有一些应用,如分析岩土结构的可靠性[13]等,但三参数区间数的应用尚未见报道.三参数区间数包含了最可能取值点的信息,其在区间内的分布是非均匀的,比二参数区间数更适于描述不确定的评价指标.由于表达形式和分布函数不同,导致对两者作风险比较的难度差别较大,详见2.6节.
2.2 模糊隶属函数
工程领域常采用线性的梯形、三角形隶属函数,来建立指标集和风险备择集之间的映射关系,但这些函数的参数均不可变,只适于简略评价单一指标的风险.多个指标由于有不同的评价标准,因此,需要引进可变隶属函数,来与多个评价标准相对应.
另一方面,建筑的风险评价标准本身存在一定的模糊性,在某些分界值附近误差较大.因此,应在这些界限值(即评价值)附近,采用分辨率较低的模糊集[14],即斜率较小的隶属函数.
因此,本文由评价值{δi1,δi2,δi3}(见1.2节),构造了更合理的4个S型可变模糊隶属函数u=uj(x)如图3所示,每个函数依次对应于4个风险等级:
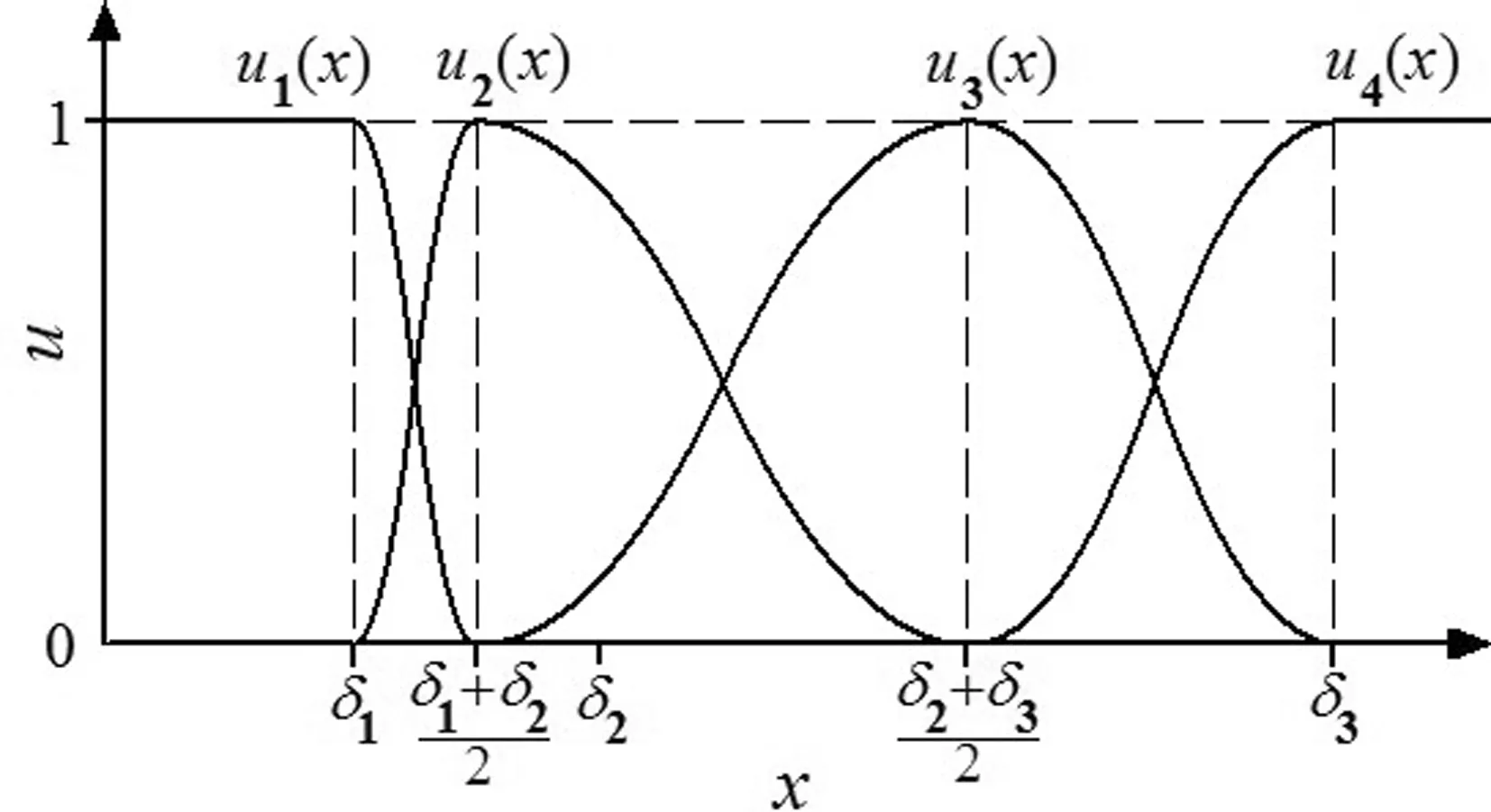
图3 S型模糊隶属函数
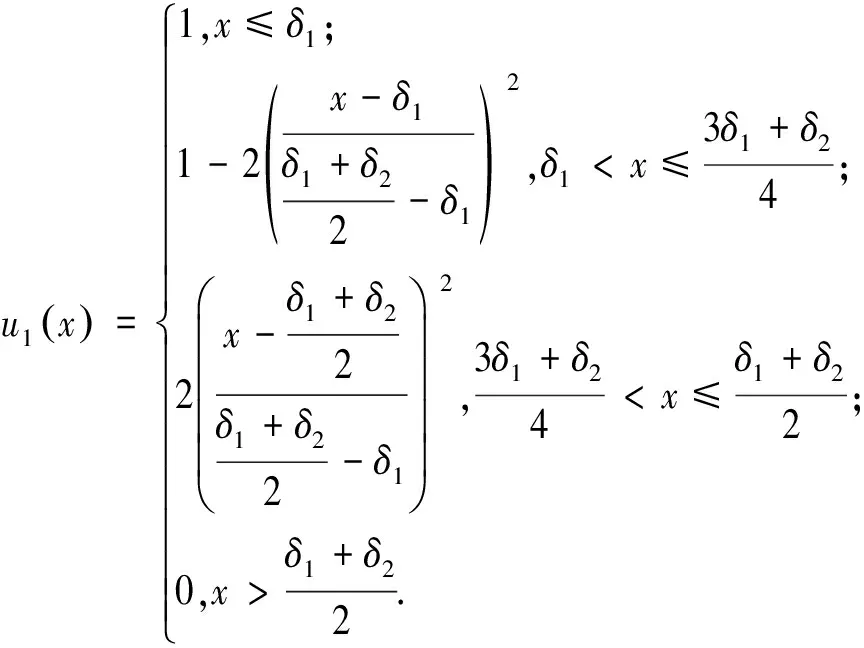
(5)
u2(x)=
(6)
限于篇幅,在此不列出u3(x)和u4(x)的表达式,但将u1(x)表达式中的(δ1+δ2)/2换成δ3,(3δ1+δ2)/4换成(δ2+3δ3)/4,δ1换成(δ2+δ3)/2,可得到u4(x)的表达式.同理,亦可由u2(x)表达式推导出u3(x)的表达式.
2.3 单因素评判矩阵
将1.1节中的代表值Xi=[xi-,xi△,xi+]代入上述四级S型隶属函数,可得其在第j风险区间的隶属度:{uj(xi-),uj(xi△),uj(xi+)},令rij-=min{uj(xi-),uj(xi△),uj(xi+)},rij△=uj(xi△),rij+=max{uj(xi-),uj(xi△),uj(xi+)},可得到单因素评判矩阵[12]:
rij∈[rij-,rijΔ,rij+].
(7)
2.4 评价指标的权重
由于建筑风险的特点,某个指标值越大时,其风险也越大,且超过某些限值时可能突发严重的损坏,相当于水筒的“短板效应”.针对普通实数的超标加权法[15]正好符合这一思想,即通过增大超标指标的权重,来更客观地描述其风险状态.因此,本文引入超标加权法,以三参数区间数的“重心”(普通实数形式,如下式中的Yi)为基础来计算权重,令:
Yi=(xi-+4xiΔ+xi+)/6,δiav=
(δi1+δi2+δi3)/3,
(8)
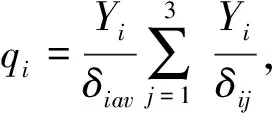
(9)
(10)
与普通实数指标不同,通过式(8)~式(10)来计算三参数区间数指标的归一化权重时,常出现某些评价指标“超标”很多,其他指标由于“超标”较少而权重很小,甚至可以忽略.因此,本文借鉴相关研究经验[14-15]进行修正,设定各指标权重的下限:
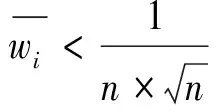
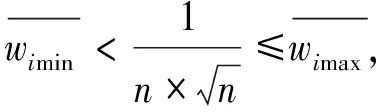
(11)
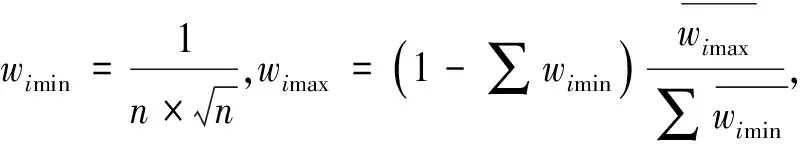
组成权重集W={wi}1×n,满足
(12)
2.5 模糊综合评判区间
将修正后的权重集与单因素评判矩阵相乘,可得到模糊综合评判区间[12]:
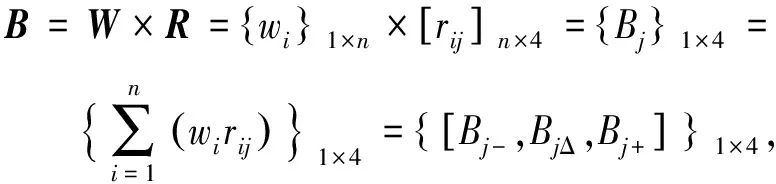
(13)
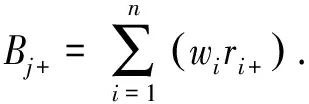
(14)
2.6 风险排序
风险评判模型一般采用可能度法[16],来对风险区间数B1,B2,B3和B4的大小排序;具体方法有多种,其中最合理的为分布函数积分法[15].
设三参数区间数X=[a,b,c],Y=[e,f,g],其分布函数依次为F(x),G(y),记X大于Y的可能度为Px>y;当Px>y=0.5时,认为X与Y等价.
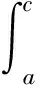
(15)
由图2可知:F(x)和G(y)均为分段函数,使得待积分的区域有20种情况,求解过程复杂,且不适于编程.为了推广使用,本文推导了全部20种工况的求解方法,详见作者的个人网站,在此省略.
根据式(15),对模糊综合评判区间B={[Bj-,Bj△,Bj+]}1×4={B1,B2,B3,B4}1×4作两两比较,即可得到风险可能度矩阵P={Pjk}4×4,其中Pjk为三参数区间数Bj大于Bk的可能度.
根据可能度矩阵P,可对B1,B2,B3和B4可能出现的大小排序;也可计算排序向量V=(V1,V2,V3,V4)T,对Vj的排序即相当于对Bj排序[16]:
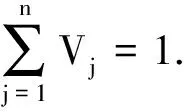
(16)
3 工程应用
3.1 风险评判流程
将评判模型(第1章)和评判方法(第2章)相结合,归纳基坑周边建筑的风险评判流程如图4所示.为了验证流程的可行性与合理性,本文在长沙地铁袁家岭站基坑工程中作了风险评判应用,并由施工监测结果进行了检验.
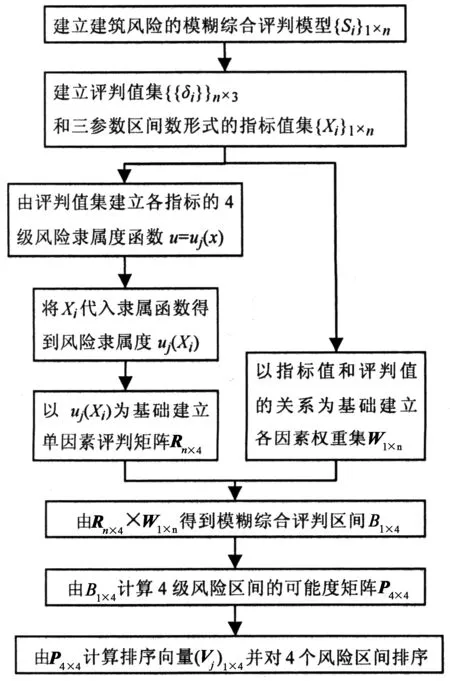
图4 风险评判流程图
3.2 工程概况
袁家岭站基坑周边有众多建筑,其中一栋7层砖混结构距基坑边缘仅3.45 m,如图5中所示的建筑A,按文献[8]可划分为大刚度建筑;车站采用明挖基坑,围护排桩的设计厚度为1.2 m,设计标准挖深为-18.4 m,远离建筑处的挖深为-18.8 m.从上至下设置三排钢筋混凝土支撑,分别支撑在-0.6 m,-8.7 m,-13.9 m处.根据地质勘察报告,从上至下分布的主土层及其平均厚度依次为:杂填土2 m,粉质粘土7.2 m,卵石4.2 m,粉质粘土1.0 m,强风化泥质粉砂岩3.4 m,强风化泥质粉砂岩>32.2 m.
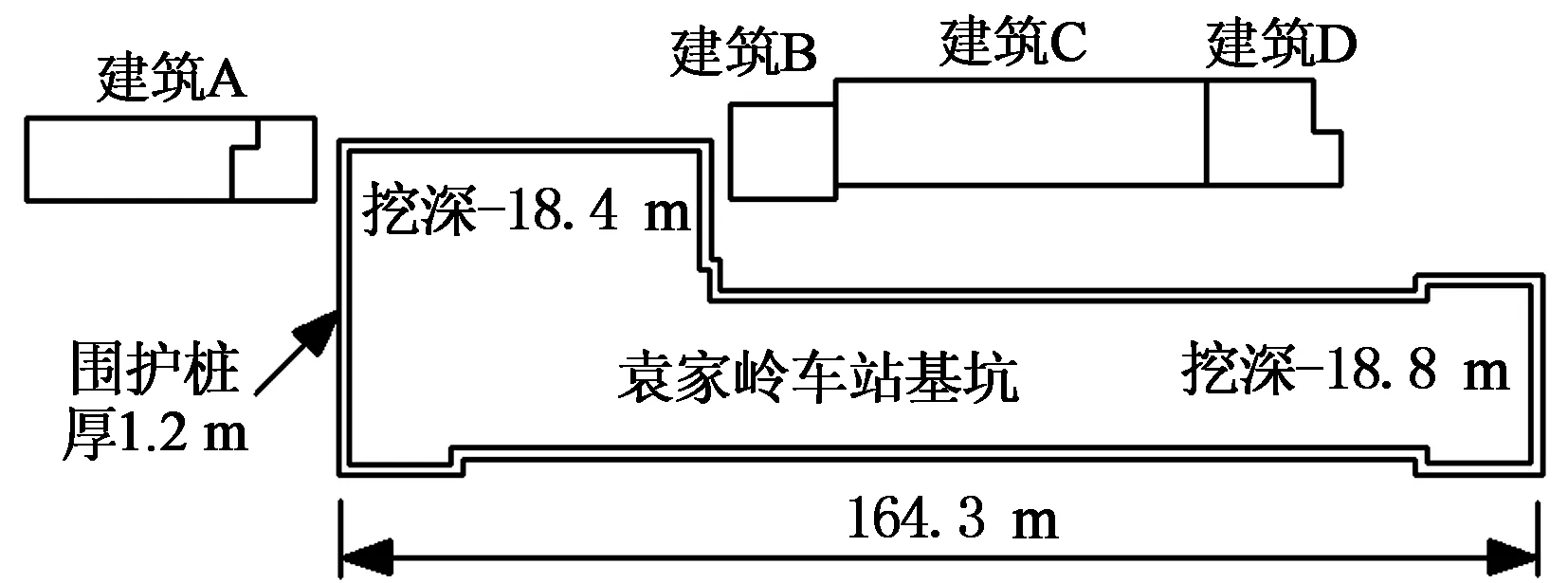
图5 基坑及建筑位置关系图
3.3 基坑施工模拟
由于建筑风险大,设计阶段对基坑和建筑沉降开展了详细的有限元模拟.采用有限元软件ABAQUS,建立三维实体模型[9],模型的竖向边界从地表向下取约2.5倍挖深,水平边界取至坑外3倍挖深,如图6所示.
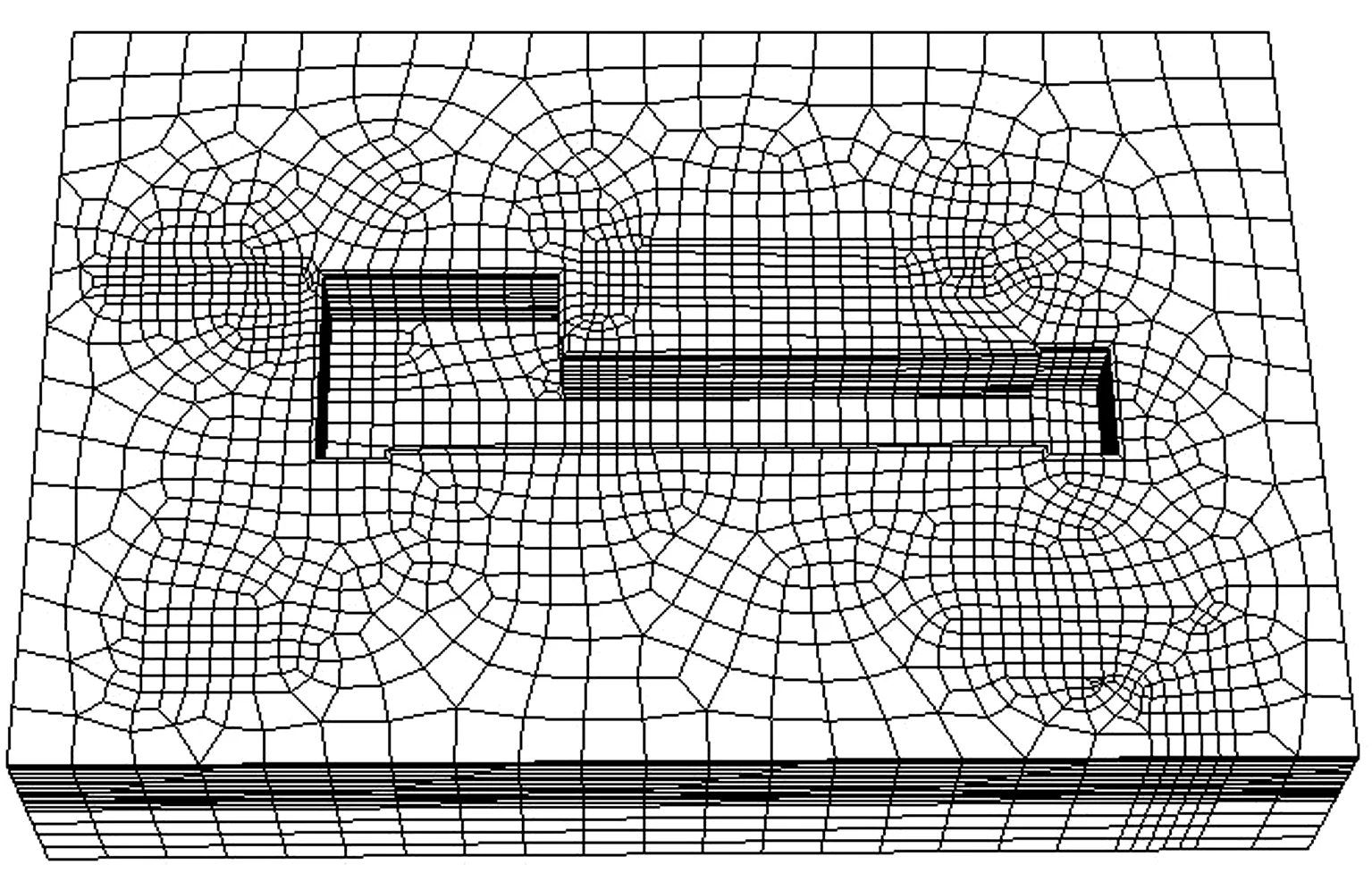
图6 三维有限元模型
模拟工作采取了一些假定:土体采用摩尔-库仑模型,考虑渗透性和排水固结作用;按结构、基础类型将建筑等效为荷载作用在地表上;考虑重力效应、建筑的初始变形;用等效荷载或指定位移模拟基坑支撑体系.
基坑开挖用杀死单元实现,坑内外的水压差引起坑底渗水;按设计方案逐层开挖、加设支撑、模拟降水;最终挖至设计挖深后,得到建筑的最大沉降值和倾斜度.
多种组合工况下的计算结果如表4[9]所示,其中“最可能”指按工程经验分析最可能出现的工况.

表4 最大沉降值和最大倾斜度的取值范围
3.4 房屋损伤鉴定
基坑开挖前对建筑A进行了损伤鉴定,部分鉴定结果如表5所示,可由此计算建筑的损伤系数.

表5 建筑鉴定结果及损伤系数
由式(1)~式(3)计算建筑的损伤系数为E=[E-,E△,E+]=[0.349,0.399,0.449],损伤等级为c~d.
3.5 风险评判
1)取表4和表5中的数据建立评价指标集S1×3,则指标值的集合X1×3为:{[24.1,51.7,86.5],[0.31,0.71,1.59],[0.349,0.399,0.449]}.
由表1和表2建立评价值集{{δi1,δi2,δi3}}3×3为:{{10,50,75},{1.2,1.6,2},{0.2,0.4,0.6}}T.
若直接由上述指标和相应的评价值分别评判风险,按沉降值评判大致应为3级,按倾斜度评判大致应为2级,按损伤系数评判应为2~3级之间,相互之间并不统一,因此需要进一步作综合评判.
2)由式(5)~式(7),得到单因素评判矩阵R3×4:

(17)
3)由式(8)~式(12),得到经修正的权重集W1×3:W={0.597,0.167,0.255}.可以看出,本模型的风险评判将主要依靠沉降值,其次为损伤系数和倾斜度,与各指标单独评判的风险危险程度一致,符合建筑的风险特点.
4)由式(13)和式(14),得到模糊综合评判区间B1×4:B={[0,0.167,0.267],[0.033,0.258,0.794],[0.031,0.576,0.748],[0,0,0.579]}.
5)上述风险区间可由主观排出大小为:3级>2级>4级>1级,但无法了解各级风险可能性的差距.因此,应按2.6节的方法计算综合评判区间的可能度矩阵P4×4:

(18)
6)由式(16),计算上述矩阵的排序向量:
V= (0.172,0.294,0.334,0.200)T.
因此,计算风险排序为3级>2级>4级>1级,最可能为3级“较高”,其次为2级“一般”.由于评判结果表明,建筑A在基坑施工期间的风险较大,以及工期紧、加固难度大、不经济等原因,建设单位放弃了对该建筑的加固,准备随时拆除.
3.6 实测结果检验
基坑施工过程中,当大部分施工段开挖至-18 m时(设计挖深约-18.4 m),建筑测点的最大沉降值为42.4 mm(略小于预测的最可能值);最大倾斜度约为0.5‰(略小于预测值的最可能值);多处裂缝超过了相关规程的限值(高于预测的损伤程度),已不适于继续使用,最终该建筑被拆除.
从3个指标的效果来看,沉降值的作用最大,且评判结果较合理;倾斜度的评判结果偏安全;按损伤系数评判的风险程度略小于实际情况;综合评判的结果基本符合实际情况.
4 结 论
本文主要提出了一套新的综合评判基坑周边风险的方法,所采用的沉降值、倾斜度、损伤系数3个指标有较全面的代表性,且能考虑指标的随机性和评判准则的模糊性.通过在实际工程中的应用,得到如下结论:
1)三参数区间数较好地体现了指标值的随机性;结合准确的可能度算法,可使评判结果更合理.
2)S型可变函数更适合在模糊的评判标准下判别风险的隶属度;超标加权方法能突出地反映不利因素对建筑风险的影响.
3)本工程中按沉降值评判较合理,按倾斜度评判的风险略大,而按损伤系数评判的风险略小.三者综合评判的风险等级则基本符合实测结果,说明本文的方法可有效地弥补前人研究的不足,使基坑邻近建筑的风险评判更加合理、有效.
[1] 刘国彬, 王卫东. 基坑工程手册[M]. 北京: 中国建筑工业出版社, 2009: 1063-1100.
LIU Guo-bin, WANG Wei-dong. Excavation engineering manual[M]. Beijing: China Architecture & Building Press, 2009: 1063-1100.(In Chinese)
[2] BOWLES J E. Foundation analysis and design[M]. New York: McGraw-Hill Book Company, 1986: 38-42.
[3] RANKIN W J. Ground movements resulting from urban tunneling: Predictions and effects[C]// Engineering Geology of Underground Movements, London, 1988: 79-92.
[4] GB 50007-2002 建筑地基基础设计规范[S]. 北京: 中国建筑工业出版社, 2002.
GB 50007-2002 Code for design of building foundation[S]. Beijing: China Architecture and Building Press, 2002.(In Chinese)
[5] 龚东庆. 深基坑引致邻近建筑物损害评估方法[J]. 岩土工程学报, 2008, 10(S1): 138-143.
GONG Dong-qing. Procedure for evaluating excavation induced damage of adjacent buildings[J]. Chinese Journal of Geotechnical Engineering, 2008, 10(S1): 138-143.(In Chinese)
[6] 边亦海, 黄宏伟. 深基坑开挖引起的建筑物破坏风险评估[J]. 岩土工程学报, 2006, 28(S11): 1892-1896.
BIAN Yi-hai, HUANG Hong-wei. Risk assessment of building damage induced by deep excavation[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(S11): 1892-1896(In Chinese)
[7] 张驰, 黄广龙, 李娟. 深基坑施工环境影响的模糊风险分析[J].岩石力学与工程学报, 2013, 32(S1): 2669-2675.
ZHANG Chi, HUANG Guang-long, LI Juan. Fuzzy risk analysis for influence of deep foundation pit excavation on surrounding environment[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S1): 2669-2675. (In Chinese)
[8] 黄宏伟, 陈龙, 胡群芳, 等. 隧道及地下工程的全寿命风险管理[M].北京: 科学出版社, 2010: 149-176.
HUANG Hong-wei, CHEN Long, HU Qun-fang,etal. Life-cycle risk management of tunnel and underground engineering[M].Beijing:China Science Press,2010: 149-176.(In Chinese)
[9] 吴朝阳, 李正农, 罗叠峰, 等. 长沙地铁袁家岭车站基坑对周边建筑影响的有限元模拟研究[C]//第19届全国结构工程学术会议论文集(Ⅱ). 北京: 清华大学出版社, 2010: 331-335.
WU Zhao-yang, LI Zheng-nong, LUO Die-feng,etal. Finite element modeling research for the impact of the yuanjialing subway station in changsha to the nearby buildings[C]// Proceedings of the 13th national conference on structure engineering(Ⅱ). Beijing:Tsinghua University Press, 2010: 331-335.(In Chinese)
[10]李瑞礼. 历史建筑损伤检测与寿命预测的数值仿真[M]. 上海: 上海科学技术文献出版社, 2005: 46-52.
LI Rui-li. Damage detection and numerical simulation of life prediction of historical building[M]. Shanghai: Shanghai Scientific and Technological Literature Press, 2005: 46-52.(In Chinese)
[11]GB 50292-1999 民用建筑可靠性鉴定标准[S]. 北京: 中国建筑工业出版社, 2000.
GB 50292-1999 Standard of appraiser of reliability of civil buildings[S]. Beijing: China Architecture and Building Press, 2000.(In Chinese)
[12]卜广志, 张宇文. 基于三参数区间数的灰色模糊综合评判[J]. 系统工程与电子技术, 2001, 23(9): 43-45.
BU Guang-zhi, ZHANG Yu-wen. Grey fuzzy comprehensive evaluation method based on interval numbers of three parameters[J]. Systems Engineering and Electronics, 2001, 23(9): 43-45.(In Chinese)
[13]蒋冲, 赵明华, 曹文贵. 基于区间分析的岩土结构非概率可靠性分析[J]. 湖南大学学报: 自然科学版, 2008, 35(3): 11-14.
JIANG Chong, ZHAO Ming-hua, CAO Wen-gui. Non-probabilistic reliability research on uncertain parameters in rock mechanics[J]. Journal of Hunan University: Natural Sicences, 2008, 35(3): 11-14.(In Chinese)
[14]谢季坚, 刘承平. 模糊数学方法及其应用[M].3版. 武汉: 华中科技大学出版社, 2006: 28-36.
XIE Ji-jian, LIU Cheng-ping. Fuzzy mathematics method and application[M]. 3rd Edition. Wuhan: Huazhong University of Science & Technology Press, 2006: 28-36.(In Chinese)
[15]徐肇忠. 专题制图中各有关专题要素求权方法的比较研究[J]. 测绘学报, 1995, 24(1): 64-70.
XU Zhao-zhong. A comparative study on weighting the related thematic features in thematic cartography[J]. Acta Geodaetica et Cartographica Sinica, 1995, 24(1): 64-70.(In Chinese)
[16]徐泽水, 达庆利. 区间数排序的可能度法及其应用[J]. 系统工程学报, 2003, 18(1): 67-70.
XU Ze-shui, DA Qing-li. Possibility degree method for ranking interval numbers and its application[J]. Journal of Systems Engineering, 2003, 18(1): 67-70.(In Chinese)
