广义逆矩阵A-的计算方法及应用
2014-09-17戴中林
戴中林
(西华师范大学 数学与信息学院 四川 南充 637002)
众所周知,求解矩阵方程AX=B时,当A为可逆方阵,则解X=A-1B;当A为不可逆方阵或为长方矩阵时,A-1失去意义.为此我们利用广义逆矩阵A-(减号逆)的概念[1-3],将求逆矩阵运算进行推广,使得无论A是何种矩阵,A-均有意义. 这时矩阵方程AX=B的解都为X=A-B,当A-为A的全部广义逆时,X=A-B为通解.特别地,当B为n维列向量时,该解即为线性方程组AX=B的通解.
1 广义逆矩阵A-(减号逆)的定义
定义设矩阵A为m×n矩阵,若存在n×m矩阵G,使得AGA=A,则称G为A的一个广义逆矩阵,记为G=A-.即有AA-A=A.
一般情况下,满足定义的A-不是唯一的.一般可求出矩阵A的一个或全部广义逆矩阵.
2 广义逆矩阵A-的计算方法
2.1 求矩阵A的一个广义逆A-的公式计算法
定理2.1设A为m×n的行满秩矩阵,即秩rA=m A-=AT(AAT)-1. 证因为A为m×n矩阵,则AT为n×m矩阵,故矩阵AAT为m阶可逆方阵,有 AAT(AAT)-1=Em, 等式两边右乘矩阵A,得A[AT(AAT)-1]A=A,故由广义逆矩阵的定义有惟一个广义逆矩阵 A-=AT(AAT)-1. 解应用上述公式可求得A的一个广义逆 证由广义逆定义即得 即R-=RT. P-1RQ-1A-P-1RQ-1=P-1RQ-1, 即R(Q-1A-P-1)R=R. 由广义逆的定义及引理得Q-1A-P-1=R-=RT,即得A-=QRTP. 定理2.3矩阵A的全部广义逆矩阵为 其中Y1,Y2,Y3为自由未知量矩阵,总共包含m·n-r2个自由未知量. 成立.故本定理成立. 解对矩阵A先后进行行及列的初等变换,即 定理3.1若A-是A的一个广义逆矩阵,则矩阵方程AX=B的通解为 X=A-B+(En-A-A)Y. 证首先证明矩阵方程AX=O的通解为X=(En-A-A)Y. 因为A-是A的一个广义逆矩阵,A-A是一个n阶方阵,由定义AA-A=A,即有A(En-A-A)=O.若令n阶方阵C=(En-A-A),则有AC=O.设Y为与C可乘的矩阵,有A(CY)=O,故取X=CY=(En-A-A)Y,则有AX=O,故X=(En-A-A)Y是矩阵方程AX=O的通解. 又矩阵方程AX=B的一个特解为X=A-B,根据矩阵方程AX=B的通解结构定理,即得通解 X=A-B+(En-A-A)Y。 解由例2.1求得的A-,代入通解公式, 其中z1,z2为自由未知量. 根据广义逆矩阵的计算方法,如果能求出矩阵A的全部广义逆A-,而广义逆中又自然带有若干个自由未知量,即可由X=A-B求得该矩阵方程的通解,且自由未知量的个数也相应确定. 定理3.2若A-为A的全部广义逆矩阵,则矩阵方程AX=B的通解为X=A-B. 利用定理3.2再解例3.1.由例2.2得A的全部广义逆A-,故通解为 其中z1,z2为自由未知量. 解对矩阵A进行行及列的初等变换,可求得 故矩阵A的全部广义逆矩阵 其中y1,…,y8为自由未知量.而通解为 其中z1,…,z4为自由未知量. 从上例可得出以下结论:由于A-的自由未知量的个数是m·n-r2,而线性方程组AX=B的自由未知量的个数本应是n-r个,显然m·n-r2≥n-r,但当计算通解X=A-B时,经中间变量代换后,自由未知量的个数就必然会从m·n-r2个减少到n-r个,否则前面的计算必有错误.这个结论即是判断求逆计算是否正确的依据. [参 考 文 献] [1] 陈祖明.矩阵论引论[M].北京:北京航空航天大学出版社,1998:218-234. [2] 周海云.矩阵理论简明教程[M].北京:国防工业出版社,2011:156-170. [3] 黄有度.矩阵理论及其应用[M].合肥:合肥工业大学出版社,2013:137-144.
2.2 求矩阵A的全部广义逆A-的初等变换法
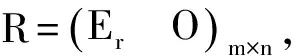

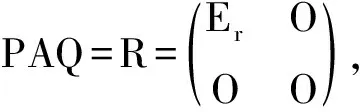
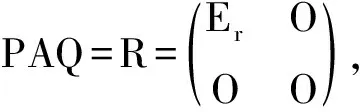
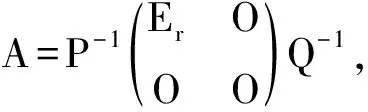
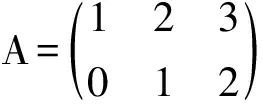
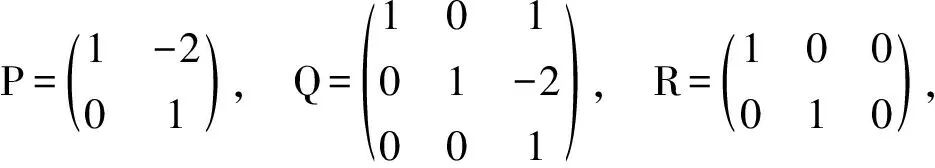

3 广义逆矩阵A-的应用
3.1 利用矩阵A的一个广义逆A-,求矩阵方程AX=B的通解

3.2 利用矩阵A的全部广义逆A-,求矩阵方程AX=B的通解