不定积分的代数解法
2014-09-17郑华盛
郑华盛
(南昌航空大学数学与信息科学学院,江西南昌330063)
众所周知,微积分学是高等数学的主要内容,积分运算与微分运算二者互为逆运算. 但积分的计算要比微分的计算更为复杂,更为灵活,更具有技巧性.文献[1]对不定积分的一些基本计算方法作了较为详细地介绍.文献[2]从微分的角度研究了不定积分的解法.本文主要从线性代数的角度研究如何求解不定积分,进而探索新的积分方法,提出一种计算不定积分的代数方法,并成功地应用于求解高等数学中几类特殊函数的不定积分.
1 主要结论
先给出有关分块矩阵逆的一个结论:
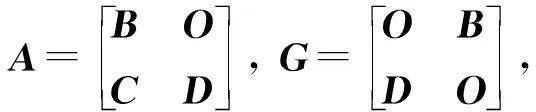

定理1设V为上全体可微函数所组成的一个线性空间,pi(x)∈V,(i=1, 2, …,n) ,p1(x) ,p2(x) ,…,pn(x)线性无关,
W=Span(p1(x),p2(x),…,pn(x)),f(x)∈W,
且微分运算D关于W是封闭的,即∀p(x)∈W,Dp(x)=p′(x)∈W,则
(i)D(p1(x),p2(x),…,pn(x))=(p1(x),p2(x),…,pn(x))A,其中A∈n×n;
(ii) 若Dp1(x),Dp2(x),…,Dpn(x) 线性无关,则A可逆;
(iii) 若A可逆,不妨设A-1=(bij)n×n,则
其中C为任意常数.
证(i)由已知,有
Dp1(x)=p′1(x)=a11p1(x)+a21p2(x)+…+an1pn(x),
Dp2(x)=p′2(x)=a12p1(x)+a22p2(x)+…+an2pn(x),
……
Dpn(x)=p′n(x)=a1np1(x)+a2np2(x)+…+annpn(x).
即
D(p1(x),p2(x),…,pn(x))=(p1(x),p2(x),…,pn(x))A,
其中A=(aij)n×n.
(ii) 若Dp1(x),Dp2(x),…,Dpn(x) 线性无关,则由
λ1·Dp1(x)+λ2·Dp2(x)+…+λn·Dpn(x)=0,
得λ1=λ2=…=λn=0 ,即
只有零解,从而得A≠0,即A可逆.
(iii) 若A可逆,不妨设A-1=(bij)n×n,则在相差任意常数的情况下,微分变换D可逆,且其逆变换D-1满足
D-1(p1(x),p2(x),…,pn(x))=(p1(x),p2(x),…,pn(x))A-1+C,
即

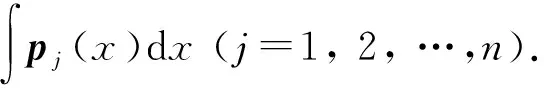
2 应用实例
为了验证本文方法的有效性,我们计算以下五种类型的不定积分.


解设f(x)=eαxcosβx, 则f′(x)=αeαxcosβx-βeαxsinβx,且由eαxcosβx及eαxsinβx求导后的表达式,可知选取基函数
p1(x)=eαxcosβx,p2(x)=eαxsinβx,
则有
D(p1(x),p2(x))=(p′1(x),p′2(x))=(p1(x),p2(x))A,


解设f(x)=cosαxsinβx, 则
f′(x)=-αsinαx·sinβx+βcosαx·sinβx,
且由sinαxsinβx及cosαxsinβx求导后的表达式,可知选取基函数
p1(x)=cosαxsinβx,p2(x)=sinαxcosβx,
p3(x)=sinαxsinβx,p4(x)=cosαxcosβx,
则有
D(p1(x),p2(x),p3(x),p4(x)) =(p′1(x),p′2(x),p′3(x),p′4(x))
=(p1(x),p2(x),p3(x),p4(x))A,
其中

而由引理1,得
其中s=α2-β2, 故由定理1得
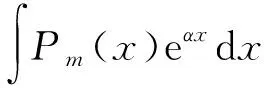
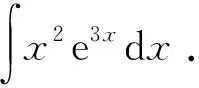
解设f(x)=x2e3x, 则
f′(x)=2xe3x+3x2e3x,
且由xe3x及x2e3x求导后的表达式,可知选取基函数
p1(x)=x2e3x,p2(x)=xe3x,p3(x)=e3x,
则有
D(p1(x),p2(x),p3(x)) =(p′1(x),p′2(x),p′3(x))
=(p1(x),p2(x),p3(x))A,
注 (i)当m较大时,A为稀疏矩阵,可将A分块后由引理1求A-1,计算并不复杂;
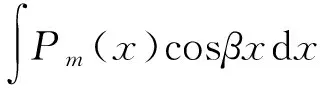

解设f(x)=x3cos2x, 则f′(x)=3x2cos2x-2x3sin2x,且由x2cos2x与x3sin2x求导后的表达式,可知选取基函数
则有
D(p1(x),p2(x),…,p8(x))=(p1(x),p2(x),…,p8(x))A,
其中

而由引理1可先求B-1,D-1,再求A-1,得
故由定理1可得


解设f(x)=xeαxcosβx, 则
f′(x)= eαxcosβx+αxeαxcosβ-βxeαxsinβx,
且由eαxcosβx,xeαxcosβx及xeαxsinβx求导后的表达式,可知取基函数
p1(x)=xeαxcosβx,p2(x)=xeαxsinβx,
p3(x)=eαxcosβx,p4(x)=eαxsinβx,
则有
D(p1(x),p2(x),p3(x),p4(x))=(p1(x),p2(x),p3(x),p4(x))A,
其中

由引理1得
其中l=α2+β2, 故由定理1得
[参 考 文 献]
[1] 同济大学应用数学系. 高等数学(上册)[M]. 5版.北京:高等教育出版社,2005:182-221.
[2] 郭鹏云,云文在,田强,陈向华,宋志平. 不定积分解法研究[J]. 大学数学,2012,28(3):149-153.
[3] 同济大学应用数学系. 线性代数[M].4版. 北京:高等教育出版社,2008:46-56;141-157.
[4] 北京大学数学力学系. 高等代数[M].北京:人民教育出版社,1978:177-189.
