Lebesgue 积分列的等度绝对连续性

王向东， 张彩霞， 戎海武

(佛山科学技术学院理学院， 广东佛山528000)

设E是Lebesgue 可测集，对于定义在E上的可测函数列fn(x)(n=1,2,…)，若对于任意的ε>0，存在δ>0，对于任意可测集e⊂E，当me<δ时，都有

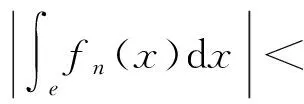
则称fn(x)的积分列在E上等度绝对连续.

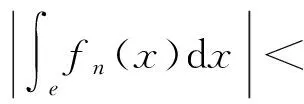
对于满足条件me<δ(e⊂E)的集e，令

于是有

从而

故得

即

故有

令δ=minδ1,δ2，则δ>0且当me<δ(e⊂E)时，有

注意到

则当me<δ,e⊂E时，

从而可知fn(x)(n=1,2,…)在E上的积分是等度绝对连续的.

定理2设mE<∞，若定义在E上的可测函数列fn(x)满足条件：

fn(x)≤g(x) (n=1,2,…)

在E上几乎处处成立，并且函数g(x)在E上可积，则fn(x)在E上的积分是等度绝对连续的.

证由于

fn(x)≤g(x) (n=1,2,…)

在E上几乎处处成立，根据积分的单调性，有

即fn(x)在E上可积.

从而

即fn(x)在E上的积分具有等度绝对连续性.

[参 考 文 献]

[1] 郭大钧,等.实变函数与泛函分析[M]. 济南：山东大学出版社，1984.

[2] 王向东,等.度量空间与Lebesgue 积分[M]. 郑州：河南大学出版社，1994.