基于分位数回归的国内黄金价格影响因素分析

2014-09-17周云丽汪金菊

大学数学 2014年4期

周云丽，汪金菊

(合肥工业大学数学学院，安徽合肥230009)

1 引言

在人类社会的经济活动中，黄金发挥着极为重要的作用，它是国家货币的储备金，是个人金融资产投资保值的工具，具有货币和商品双重属性.黄金价格自然也受到各国的关注，而黄金作为一种特殊的产品，其价格的影响因素是多方面的.

关于国际黄金价格的影响因素的研究，国内外学者得出了不少具有实证意义的结论.国际上，Graham Simith[1]选用美国的四个黄金价格和六个股票价格数据通过实证分析得出黄金价格与主要股票指数(如美国道琼斯指数)之间存在负相关关系，并通过格兰杰因果检验发现美国股票收益单向影响黄金价格.Capie，Mills和 Wood[2]通过对美元汇率、英镑汇率和日元汇率的相关性展开研究，结果证实黄金价格与上述三种汇率之间存在负相关关系.Colin Lawrence[3]通过简单的相关性检验和使用动态VAR分析研究得出石油价格和黄金价格之间具有显著相关关系等.国内也有不少此方面的研究，傅瑜[4]对黄金价格与美元汇率、证券价格、GDP、石油价格的关系进行了相关性分析，并建立了单因素回归模型，结果表明黄金价格与这些因素之间都是呈现负相关关系.杨柳勇和史震涛[5]运用简单回归分析的方法讨论了黄金价格的长期决定因素，结果表明股价指数和汇率对黄金价格有负的影响，通货膨胀率与利率对黄金价格有正的影响.樊元和王群[6]利用非线性的Markov区制转换VAR模型和脉冲响应方法分析了货币政策与黄金价格之间的关系，实证结果表明货币政策对于黄金价格的影响在金价的上涨期和下跌期的作用效果和响应时间是有所不同的.

我国发现和使用黄金的历史非常悠久，并且也一直将其作为权势和财富的象征.新中国建立初期只能从新生产的黄金中获得黄金储备，没有历史的积累.黄金开采企业必须将产出的黄金交给人民银行，再由银行配给用金单位，国内黄金市场一直是封闭的.直到2002年10月30日，上海黄金交易所正式运行，中国黄金市场才开始全面对内开放，而黄金交易的品种也日益丰富.2008年1月9日，黄金期货在上海黄金交易所挂牌交易，实现了中国黄金市场由商品市场向金融市场的转变.我国黄金市场是进入新世纪以来发展最为迅速的新型市场之一，上海黄金交易所已成为全球交易量第一的场内实金交易市场.黄金饰品的需求量在2010年已超过300吨，成为仅次于印度的全球第二大首饰市场.居民的黄金投资需求旺盛，在短短几年内就形成了一个多形态市场组成的黄金投资市场体系.

随着国内黄金市场的发展，关于国内黄金价格的影响因素的研究近年来成为一个热点，叶莉和周砚青[7]运用普通最小二乘法建立多元回归模型，对影响我国黄金市场价格的因素进行实证研究，并利用Granger因果关系检验了黄金市场价格变动与其它金融市场的关联性，研究结果表明，黄金市场与外汇、货币、资本市场间存在着较强的联动性.文胜雄[8]通过建立中国黄金价格，经济增长率和上证指数这三个变量之间的关系，探求中国黄金价格与经济增长率和上证指数的相关性，结果表明中国的黄金价格与GDP和上证指数都具有正相关关系.王珏[9]利用相关性检验讨论了中国宏观经济数据与国内黄金的关系，并运用最小二乘法对建立的多元回归模型进行分析，结果表明消费者物价指数与国内黄金价格同向变动，汇率和利率与黄金价格反向变动，但是中国经济数据尚不能很好的解释黄金价格的变动.钟欣然[10]以通货膨胀预期及国内金价为变量建立自适应预期模型，并将其转化为一阶自回归模型，结果表明在其他影响因素不变的情况下，人们对未来通胀预期值越高，金价越高等等.

国内外的研究结果为本文研究黄金价格波动的影响因素提供了很好的基础和参考价值.众多学者对黄金价格进行实证分析时通常采用最小二乘估计方法，这种方法只能度量自变量对因变量的平均影响，而无法体现在条件分布不同位置时自变量对因变量的影响差异，这样大量重要信息就被淹没了.而分位数回归可以很好的解决这个问题，因此本文采用分位数回归模型对黄金价格的影响因素进行分析研究.以中国黄金交易市场的黄金价格为研究对象，基于世界原油价格、道琼斯指数、美元汇率、上证指数、利率的经济数据，建立国内黄金价格多因素分位数回归分析模型.

2 分位数回归的基本思想

分位数回归最早由Koenker和Bassett[11]于1978年提出来的，它是对以古典条件均值模型为基础的最小二乘法的延伸，分位数回归依据因变量的不同分位点对自变量进行回归，可以得到所有分位点下的回归模型，即用几个分位函数来估计整体模型.分位数回归法的特殊情况就是中位数回归，也就是通常的最小二乘回归，用对称权重解决残差最小化问题，而其他条件分位数回归则需要用非对称权重解决残差最小化.

一般地，分位数回归模型方程为

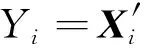
得到τ分位数上的参数估计值，因此对于不同的τ∈(0,1)得到不同的回归模型.

相对于普通最小二乘回归，分位数回归具有四个方面的优势：①分位数回归模型特别适合具有异方差性的模型；②对条件分布的刻画更加的细致，每个分位点回归都赋予条件分布上某个特殊点(中央或尾部)一些特征；把不同分位点的回归集中起来就能给出一个关于条件分布的更完整的统计特征描述.并且不同分位点下的参数估计本身也可能具有进一步探讨的意义；③分位数回归不需要对模型中的随机扰动项做很强的分布假设，在扰动项非正态的情况下，分位数回归估计可能比最小二乘估计更为有效.④与最小二乘回归通过使误差平方和最小的参数的估计不同，分位数回归通过使加权误差绝对值之和最小得到参数的估计，因此估计值不容易受到异常值的影响，从而估计更加稳健.

实际上，求解

的过程十分复杂，目前常用的方法有单纯形法、内点法、平滑算法等. 而这些计算方法一般都要利用计算机并通过迭代方法进行求解，分位数回归在大部分统计软件(Sas，Stata，Eviews，R等)中都能实现.

3 国内黄金价格的分位数回归模型

国际金价主要受原油价格、主要工业国家的股票指数、美元汇率、黄金储备、国际政治事件等复杂因素的影响，而国内黄金价格(G)的波动更为复杂，除上述国际因素外，本国的经济状况也会对其产生影响.基于经济学上的基本原理以及对国内黄金价格走势和相关影响因素的变动趋势的分析，本文选取以下几个因素建立黄金价格的回归分析模型.

(i)石油价格(RBRTE).石油是重要的战略资源和经济资源，是衡量世界经济发展的指标.石油价格过高往往会引发通货膨胀，而黄金作为重要的保值商品必然会吸引更多的投资者，从而加大黄金的需求，提高了黄金价格，石油价格一直是黄金价格的风向标.本文选取能代表世界石油价格的布伦特原油价格(RBRTE).

(ii)道琼斯指数(DJIA).由于黄金具备抗风险的作用，在投资组合中常被用来冲抵部分风险.一般金融市场的规律是：股票市场涨，资金流入多;股票市场跌，资金流出多.流出去的资金部分流入黄金市场，进而推动了黄金价格的上涨.道琼斯指数作为影响国际黄金价格的因素被引入到该模型中.

(iii)美元汇率(USD).众多研究表明，美元汇率与黄金价格有很强的联动性.一方面，由于美元与黄金一样是国际储备资产，美元坚挺就削弱了黄金作为储备资产和保值功能的地位，即美元涨，金价跌；反之，美元跌，金价涨.

(iv)上证指数(SH).股票市场和黄金市场是我国金融市场的有机组成部分，作为两种重要的投资产品，两者之间必定有一定的联动性.本文选取了国内重要的股票指数：上证指数.

(v)利率(SHIBOR).这里利率作为黄金替代品价格被引入到模型当中的，因为利率可以作为衡量其他一切资本的价格，利率波动也就代表其他资产的波动，利率和黄金价格的波动有一定的关系.该模型中利率选取的是中国银行间隔夜拆借利率.

建立国内黄金价格的分位数回归模型如下：

Gt=β0(τ)+β1(τ)RBRTEt+β2(τ)DJIAt+β3(τ)SHt+β4(τ)USDt+β5(τ)SHIBORt+εt，

(1)

其中β0(τ) ,β1(τ),β2(τ),β3(τ),β4(τ)和β5(τ)分别表示对各个变量进行参数估计的第τ分位数的系数，εt为随机误差项.

4 实证分析

4.1 数据的来源及分析处理

本文选取的数据时间是2008年1月到2013年6月(共1326个数据)，其中国内黄金价格来自上海黄金交易所的AU99.95现货黄金价格，石油价格、道琼斯指数和上证指数的数据来自雅虎金融网，美元汇率来自中国人民银行，利率的数据来自东方财富网数据中心.实验所用的软件为Eviews6.0.

在建模之前，我们对上述六个变量的时间序列做了一般性的统计分析，分析结果由Eveiws6.0得出，详见表1.从表1中可以看到，黄金价格序列的偏态系数约为-0.091078，峰态系数约为1.646249，J-B统计量显示其不服从正态分布，且有轻微的左偏现象.而其他五个序列也都不是正态分布.由此可以看出这里所使用的数据都具有非正态性、非对称性的特点，如果采用最小二乘法进行回归分析则会使结果可能出现偏误.

表1 数据的统计描述

一般地，对于时间序列模型，建模之前通常要先对序列进行平稳性检验，以保证建模的有效性. 本文采用ADF单位根检验，结果见表2.由表2结果可知，G，RBRTE，DGIA, USD，SH，SHIBOR这六个时间序列中只有SH是平稳的，其他都是不平稳的.对于非平稳时间序列，Engle和Granger[13]提出了协整理论，即一些经济变量本身是非平稳时间序列，但是，它们的线性组合却有可能是平稳的，所以我们运用Johansen方法对上述变量做协整关系检验，结果见表3.

表2 各变量单位根检验结果

表3 协整检验结果

从表3可以看出，在选定的0.05的检验水平下，149.3090>95.75366, 83.67228>69.81889, 38.96378<47.85613.所以这六个序列之间至少有两组解，即G，RBRTE，DJIA，USD，SH，SHIBOR之间存在协整关系.故模型(1)的建立具有一定的合理性.

对于上述非平稳时间序列，除了建立模型(1)这种方法，我们还可以将其平稳化，利用平稳化之后的数据建立新的模型.而一般平稳化采取差分处理的方法，一阶差分之后的检验结果见表2，表2结果显示一阶差分后的时间序列是平稳的.因此，为了与模型(1)进行比较，我们还考虑了下面的分位数回归模型：

ΔGt=φ0(τ)+φ1(τ)ΔRBRTEt+φ2(τ)ΔDJIAt+φ3(τ)lnSHt+φ4(τ)ΔUSDt

(2)

4.2 模型对比分析和实证结果分析

上面我们分别基于非平稳的原时间序列和差分处理后的平稳时间序列建立了国内黄金价格的回归分析模型，为了选择更有效的模型，运用Eviews6.0软件对模型(1)和模型(2)进行分位数回归，系数估计结果分别见表4和表5.为了便于比较，表中同时给出了最小二乘回归系数估计结果.

表4 模型(1)的分位数回归和最小二乘回归系数估计结果

注1 ***，**，*分别代表1%，5%，10%水平上显著.

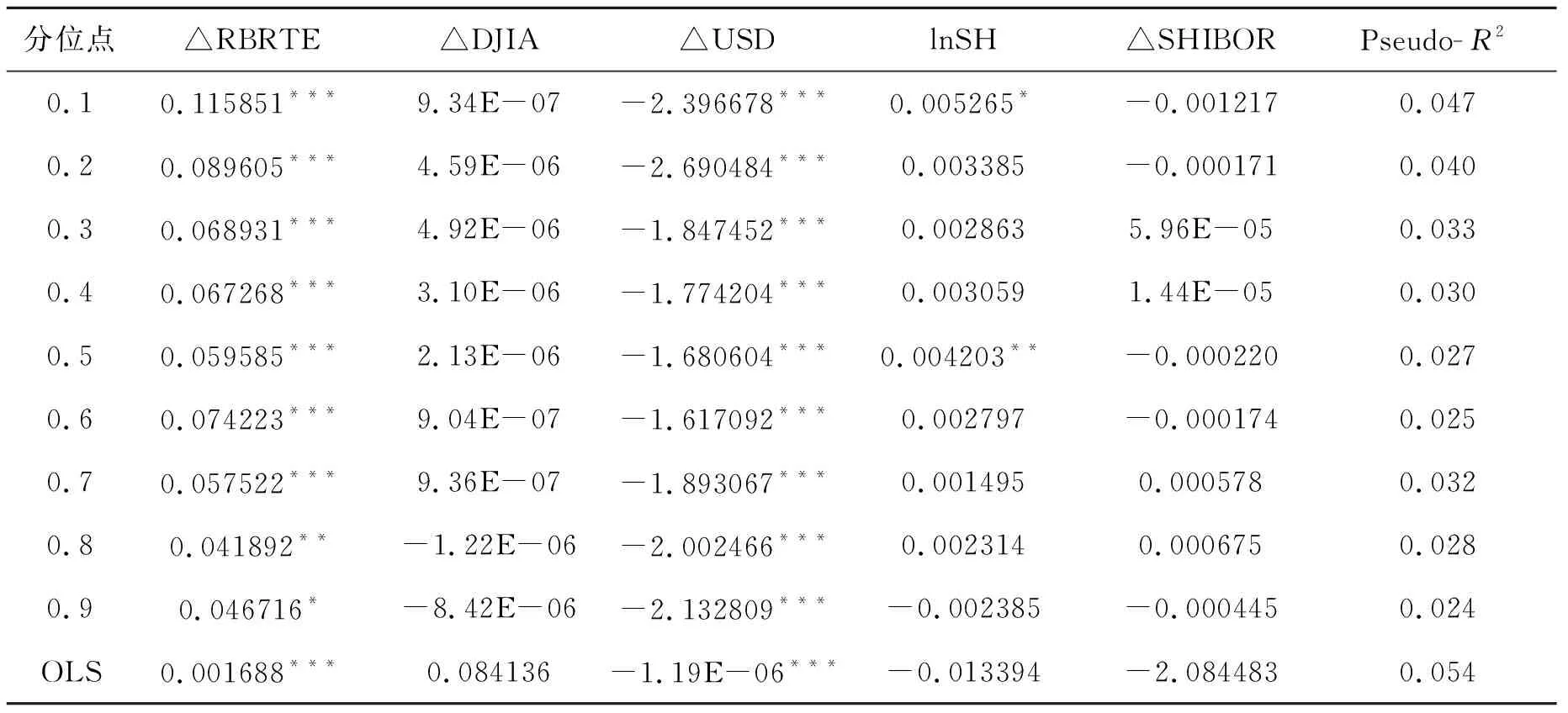
表5 模型(2)的分位数回归和最小二乘回归系数估计结果

注1 ***，**，*分别代表1%，5%，10%水平上显著.

在对模型(1)和模型(2)进行系数估计时，表4和表5分别给出了两个模型的10个分位点上的分位数回归结果和最小二乘回归结果.从结果看：(a) 模型(1)和模型(2)的回归估计的系数符号基本一致，只有DJIA这一解释变量的系数估计值的符号不同，但其在模型(1)中通过了显著性检验，从这一点来看模型(1)更能反映DJIA与G之间的关系.(b) 从各个解释变量的系数估计值的大小来看，对数据进行差分会削弱各解释变量与被解释变量G之间的关系.也就是说，可能在进行差分平稳化处理时我们丢失了原数据的某些信息，导致模型中多个变量系数估计结果数值较小且不显著.(c) 表4和表5的最后一列反映了两个模型的拟合优度，模型(1)的拟合优度明显好于模型(2).

虽然非平稳时间序列经差分后变换成平稳时间序列，但是差分变换后的序列对所讨论的经济问题有一定的局限性，并且有时变换后的序列通常都不具有直接的经济意义，使得化为平稳时间序列后所建立的模型不便于解释.因此模型(1)更能说明各个因素对国内黄金价格的影响.

表4显示了模型(1)的分位数回归和最小二乘回归系数估计结果，相对于最小二乘回归只能给出原油价格、道琼斯指数、美元汇率、上证指数、利率对国内黄金价格的平均影响效果而言，分位数回归给出的是处于不同分位数水平时各个变量对国内黄金价格的影响，对比发现分位数回归挖掘出了更多的信息：

①美元汇率作为一种国际常用汇率对黄金价格的影响比较大，影响效果显著且稳定，表现出较强的负相关，也即美元汇率每上涨1个百分点，就会带来约3个百分点的国内黄金价格的下跌.但是，在0.8，0.9高分位点和0.1低分位点处，其对黄金价格的影响效果相对减弱.由于黄金和美元都可以作为国际储备资产，美元升值就削弱了黄金的地位；反之，美元贬值就会抬高黄金的储备功能.但是黄金价格过高或过低时，相对的风险也大一些，这时美元对其影响自然就小一点.

②从表4第三列估计结果的符号看，道琼斯指数与国内黄金价格是负相关，从黄金价格低分位点到高分位点，道琼斯指数对其影响呈现U型关系，而且除了在低端分位点不显著外，在其他分位水平上均显著呈U型关系，说明在黄金价格较低和较高的时候，道琼斯指数对黄金价格的抑制作用较大，也就是说黄金作为保值工具的风险较大时，股票作为另一种保值工具就会受到更多的青睐.

③从此模型的分位数估计的结果中我们得到这样的结论：石油价格对国内黄金价格的影响在0.1-0.3低分位点显著表现出约0.51的影响力，从0.4分位点到更高分位点影响都不显著了，也就是说石油价格作为黄金价格的风向标只有在黄金价格平稳较低的时候其影响是显著且稳定的.在0.6分位点时石油价格对国内黄金价格的影响表现出了较小的抑制作用，虽然不显著，但也可能在某些时候在其他因素的影响下，黄金和石油价格的运动趋势会发生背离.而最小二乘回归得到的结果只有一个，表现为石油价格对黄金价格的平均影响效果；模型(1)的估计结果显示它与分位数回归低分位点的结果比较接近，显然当黄金价格处于高分位点时最小二乘的结果就会出现较大的误差.

④表4第五列给出了上证指数的系数估计结果，可以看出，上证指数与国内黄金价格呈显著正相关，但影响力较小.一般情况下，表现出约0.05左右的影响力，而当黄金价格较高或较低时，其影响力减弱，约为0.02左右.综合来看国内股票价格对国内黄金价格的影响比较稳定而且它们成正相关关系，在我国这样一个严格控制的经济体内，资金的流出受到严格控制，多余的资金的流向有多种选择，从而导致国内黄金价格与国内股票价格呈正相关.

⑤从最小二乘回归估计结果看，利率对国内黄金价格的平均影响力约为0.65，且呈负相关.表4中分位数回归结果分析可知，在中低分位点上黄金价格与利率呈显著正相关，利率上升导致黄金价格上升，影响力在2.0左右，而在较低和较高分位点其影响表现出明显的差异性，就其影响力来看，在尾部的影响比较大.这就说明在不同分位点处利率对黄金价格的影响波动很大，仅仅用最小二乘估计的结果去说明两者之间的相关性存在很大误差.

综上，在对黄金价格的影响因素进行分析时，分位数回归模型表现出较明显的优势.相对于最小二乘回归只得到的单一结果，即各个因素的平均影响效果，分位数回归可以根据分位点的选取得到不同的回归分析模型.比较表4中模型(1)的九个分位点回归结果：从模型的拟合优度来看，各个分位点的结果相差不大，相对来说中等分位点的拟合优度较高约为0.64；从各个因素变量的系数估计显著性来看，在低分位点处的模型结果都通过显著性检验，说明各因素对黄金价格的影响在黄金价格较低时更为显著.

5 结论和不足

本文以上海黄金交易所具有代表性的AU9995黄金价格为研究对象，经过建模前的分析和模型比较，最终选取原油价格、道琼斯指数、美元汇率、上证指数、中国银行隔夜拆借利率几个影响因素建立回归分析模型，运用分位数回归模型分析国内黄金价格的影响因素，并与最小二乘回归方法进行比较，得到以下结论：

第一，在该模型中，国内黄金价格与美元汇率、道琼斯指数之间显著呈负相关关系，与上证指数显著呈正相关关系，这与之前的理论分析部分的结果基本一致.分位数回归结果还表明在黄金价格的不同分位点它们的影响力有的有着明显的不同.

第二，该模型中原油价格对国内黄金价格的影响在不同分位点是不稳定的，但总体表现出正相关关系.一直以来原油价格都被视作黄金价格升降的信号灯，高油价加剧通货膨胀，剧烈的通货膨胀引发金价上升.分位数回归结果表明，其影响力在中间分位点和尾部之间表现出了明显的差异，也就是说黄金价格与原油价格之间长期存在一种非确定数字比例的正向联动作用，同时结果也表明这种关系也并不是绝对的，黄金价格和石油价格的运动趋势有时也可能会发生背离.

第三，利率是资金的价格，作为影响一切资产的重要因素，它直接影响着金融资产的价格和收益状况.利率上升，投资一般性金融市场的收益也就会上升，同时也伴随着风险的上升，从而黄金投资就会成为一种较好的投资.在该分位数回归模型中，银行隔夜拆借利率对国内黄金价格的影响的回归分析的结果与相关性分析的结果一样都表现为正相关关系.

第四，关于股票价格与黄金价格的反向关系已经被许多研究所证实，但从该模型结果中我们却发现，国内黄金价格与道琼斯指数之间存在负相关关系，而与上证指数存在着正相关关系，这与中国严格的资金流出的严格控制有关，在严格控制的经济体内，充沛的资金可能选择进入多个市场，从而导致国内黄金价格与国内股票价格(上证指数)呈正相关关系.

本文中使用的是2008年1月到2013年6月共1326个数据，是中国黄金市场进入新的阶段以来的这些因素的长期平均影响效果.当然，一国国内的黄金价格的波动比较复杂，不仅受文章中讨论的这些因素的影响，一国的经济状况(如GDP)、通货膨胀等因素也会对其产生影响.短期内一些突发事件、某些国家的政治经济危机、一些国家和组织对黄金的抛售等也会对国内的黄金价格产生影响，这些将是我们的后续研究内容.

[参考文献]

[1] Graham Smith.The price of gold and stock price indices for the United States[R].The World Gold Council,2001.

[2] Forrest Capiea;Terence C. Millsb and Geoffrey Wooda.Gold as a hedge against the dollar[J].Journal of International Financial Markets, Institutions and Money,2005,15(4):343-352.

[3] Colin Lawrence.Why is gold different from other assets An empirical investigation[R].The World Gold Council,2003.

[4] 傅瑜.近期黄金价格波动的实证研究[J].产业经济研究,2004,(1):30-40.

[5] 杨柳勇,史震涛.黄金价格的长期决定因素分析[J].统计研究,2004,(6):21-24.

[6] 樊元，王群.货币政策对黄金价格的影响研究[J].商业时代,2013(2):55-57.

[7] 叶莉,周砚青.中国黄金市场价格影响因素的实证研究[J].河北工业大学学报,2012,2(4):15-20.

[8] 文胜雄.中国黄金价格，经济增长率与上证综指相关性探究[J].生产力研究,2012,(4):84-85.

[9] 王珏.中国宏观经济数据与黄金价格的关系[J].探求,2012(2):96-104.

[10] 钟欣然.通货预期对国内黄金价格的影响—基于自适应预期模型[J].中国商贸，2013,(14):116-117.

[11] Koenker R, Bassett G Jr. Rgression quantile[J].Econometrica,1978,46(1):33-50.

[12] 李育安.分位数回归及应用简介[J].统计与信息论坛,2006,21(3):35-44.

[13] Engle,Robert F and GrangerC W J. Co-integration and error correction:representation, estimation,and testing[J].Econometrica,1987,55(2):251-276.

[14] 孙毅.黄金价格变动影响因素及未来走势分析[J].大连海事大学报,2011,10(6):6-10.