基于模糊偏好关系的工艺资源评价与选择的多准则群决策方法

刘晓军 倪中华 杨章群

(东南大学机械工程学院，南京 211189)(江苏省微纳生物医疗器械设计与制造重点实现验室，南京 211189)

基于模糊偏好关系的工艺资源评价与选择的多准则群决策方法

刘晓军 倪中华 杨章群

(东南大学机械工程学院，南京 211189)
(江苏省微纳生物医疗器械设计与制造重点实现验室，南京 211189)

摘 要:以加工操作序列的选择过程为例，提出了基于模糊偏好关系的工艺资源评价与选择的多准则群决策方法.首先将加工效率、加工成本、设备负载、尺寸精度、表面粗糙度、形状精度和位置精度等评判准则分为定性、定量2种模糊偏好类型，实现定性模糊偏好准则的定量化，建立定量模糊偏好准则的隶属度函数.基于此，建立各评判准则的模糊偏好矩阵，并基于C-IOWA算子对多个决策专家的评估结果进行集结，生成一致性模糊偏好矩阵.然后，求出评判矩阵的排序向量，从而实现对备选加工操作序列评价和选择.最后，通过实例验证该方法的有效性.

关键词:工艺资源选择;模糊偏好关系;多准则群决策;定量化;隶属度函数

工艺规划的一个重要任务是为制造特征选择合适的制造工艺资源，工艺资源选择的合理性保证了工艺的优化性和合理性，工艺资源选择的速度决定了工艺设计的效率.所以，研究工艺资源的评价和选择方法，实现工艺资源的智能推荐和自动选择，对提高工艺设计智能化和自动化水平，提高工艺设计效率具有重要现实意义.

有许多学者利用模糊偏好关系解决选择问题，Garcia 等［1］和 Ertay［2］利用模糊偏好关系解决群体决策问题.Amindoust等［3］建立了模糊排序模型进行供应商选择.Chen等［4］利用模糊偏好关系解决了供应商选择问题.Wu［5］研究了综合运用数据包络分析法，并对模糊偏好关系进行绩效评价.

也有许多学者对工艺资源的评价和选择方法进行了研究，主要包括基于人工神经网络、模糊算法、知识及专家系统等方法.Deb等［6］根据领域知识，建立了为对称回转类零件选择可行加工操作序列的BP神经网络.秦宝荣［7］应用模糊综合推理的理论和方法解决了特征加工方案的选择问题.肖九一等［8］应用模糊数学和模糊决策理论建立了基于模糊偏好关系的制造工艺资源评价数学模型，解决了工艺资源评价和选择中的决策与排序问题.Radwan［9］在分析了零件表面特点与加工操作间关系的基础上，建立了可用于加工操作选择的专家系统，并给出了特征面与加工操作序列的映射图.Jiang等［10］在利用成组编码为设计特征进行编码的基础上，建立了用于为特征选择加工过程的专家系统，该系统可为平面、台阶、槽、腔体及孔等特征选择合理的加工操作.

上述研究中，基于人工神经网络和模糊理论的评价和选择方法，考虑了匹配过程中的多个评判准则，但仅考虑了一个决策专家的评判结果，由于决策专家评判结果的局限性，使得匹配结果不能完全反映实际生产中复杂多变的情况;基于专家系统和知识的匹配方法中，匹配规则和知识扩展性不够，且系统的适应性差，匹配规则中没有涉及的特殊情况不能很好地处理.本文将同时考虑多决策专家和多评判准则，采用基于模糊偏好关系的加工操作序列评价和选择方法，实现了制造特征与操作序列的匹配.

1 加工操作间的模糊偏好关系矩阵

定义1［11-13］对于∀~A，~B，~C∈P，若模糊偏好关系矩阵R满足如下条件:

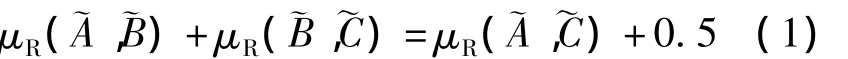
则称R是完全一致性模糊偏好关系矩阵，简称完全一致性偏好矩阵，完全一致性偏好矩阵具有互补性和中值传递性［11-13］.

定理 1［13］对于模糊偏好矩阵 R=(rij)n×n，若对其进行如下数学变换:

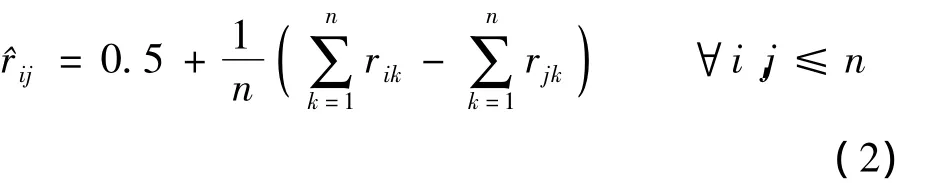
则由此建立的矩阵=(ij)n×n满足加性一致性.

加工操作序列的选择过程，是在综合考虑加工效率、加工成本、设备负载及加工精度等因素的基础上，为某一或一组制造特征从备选操作序列集合中选择合适的加工操作序列的过程.

其中，决策方案集是备选操作序列集合O={o1，o2，…，oi，…，on}，n≥2，其中，oi为第i个备选方案.设备评估准则集为Q={q1，q2，…，qj，…，qm}，m≥2，其中，qj为第j个评估准则.工艺专家或经验丰富的工艺师构成了决策群体，即T={t1，t2，…，tk，…，tl}，l≥2，其中，tk为第k个决策者.

评估准则主要包括加工效率、加工成本、设备负载、尺寸精度、表面粗糙度、形状精度、位置精度.其中，尺寸精度、表面粗糙度、形状精度、位置精度4个准则可以给出精确的偏好区间边界值，采用定量形式.加工效率、加工成本和设备负载3个准则难以用精确的数值表示，而是采用自然语言等模糊信息的表示方式，即采用定性偏好.

1.1 定性模糊偏好的定量化

为了实现对定性模糊偏好的判断，首先将定性偏好的概念空间映射成数值空间，也就是定性模糊偏好的定量化.定性模糊偏好数量值的确定是一个从概念到数值，从概念空间到数值空间的转化过程［14］.

针对不同的评估准则，首先将目标定义为模糊语言变量，建立用于描述各偏好区间的语言值集.以加工成本为例，语言值集为{“非常高(EH)”，“很高(VH)”，“高(H)”，“较高(QH)”，“中等(M)”，“较低(QL)”，“低(L)”，“很底(VL)”，“非常低(EL)”}.采用三角模糊数表示上述9级模糊语言值，偏好区间如图1所示.

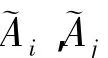
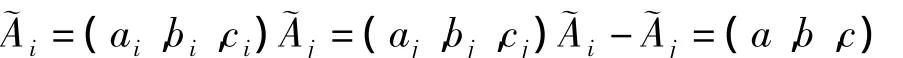
针对定性评估准则，一致性模糊偏好矩阵的求解方法如下(方法1):

①根据工艺专家针对第j个评估准则对各加工操作序列的评定，对各方案进行两两比较，利用式(3)建立各个专家的模糊偏好关系矩阵.

②根据式(2)对模糊偏好关系矩阵进行一致化处理，得到互补一致性矩阵Rk j.

1.2 定量模糊偏好

采用分段函数定义尺寸精度、表面粗糙度、形状精度、位置精度等4个准则的隶属函数，以尺寸精度和表面粗糙度为例介绍隶属函数的定义方式.

1.2.1 尺寸精度的隶属函数

假设某一个加工操作序列的尺寸精度范围为DH～DL，而被加工特征的尺寸精度为D.由于尺寸精度的等级越大，要求越低，越容易满足.当D＜DH时，该加工操作序列不能满足加工特征的尺寸精度要求，它的隶属度为0.当DH＜D＜DH+1时，该加工操作序列有可能保证加工精度，但对工人的操作技能、设备的状况有较高的要求，所以此时的隶属度应小于1.当DH+1＜D＜DL时，该加工操作序列完全可以保证加工精度，但有可能没有完全发挥该加工操作序列的能力，造成一定程度加工资源的浪费，所以此时的隶属度应等于或小于1.当D=DH+1时，该加工操作序列既能充分满足尺寸精度的要求，保证加工质量，同时也充分发挥了该加工操作序列的加工能力，减少了优势工艺资源的浪费，所以此时的隶属度为1;随着尺寸精度要求的降低，加工质量肯定能得到保证，但加工操作序列的加工能力的发挥程度却越来越小，所以隶属度会不断下降;当D=DL时，隶属度为0.8;当D=DL+1时，此时已经远不能发挥该加工操作序列的能力，所以此时隶属度为0.3;当D＞DL+1时，一般不选用该加工操作序列，所以隶属度为0.

根据加工操作序列尺寸精度上下限间相差级数，尺寸精度与加工操作序列之间的模糊映射的隶属函数有2种定义方式.

式中，DH，oi，DL，oi分别为操件序列oi的加工精度的上、下限.

隶属函数的分布曲线如图2(a)所示.当相差级数为1级时，即|DH－DL|=1，隶属函数如下式所示:

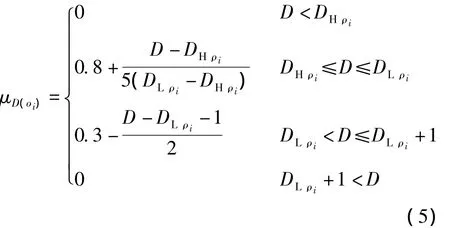
隶属函数的分布曲线如图2(b)所示.

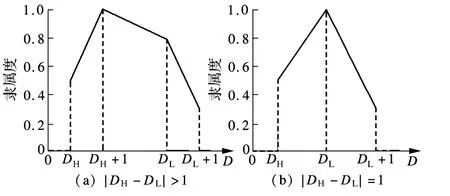
图2 尺寸精度的隶属函数的分布曲线

位置精度、形状精度与加工操作序列之间的模糊映射隶属函数的定义方法与尺寸精度相似，这里不做详细介绍.

1.2.2 表面粗糙度的隶属函数

表面粗糙度与尺寸精度具有相似的特点，表面粗糙度值越小，就越难满足加工要求，对加工操作序列的要求就会提高.假设某一个加工操作序列的表面粗糙度范围为HH～HL，而被加工特征的表面粗糙度为H.由于表面粗糙度的标准系列近似成等比数列，所以在定义它与加工操作序列之间的模糊映射的隶属函数时，需要对粗糙度值进行预处理，即

1.2.3 一致性模糊偏好关系矩阵

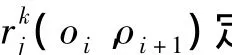
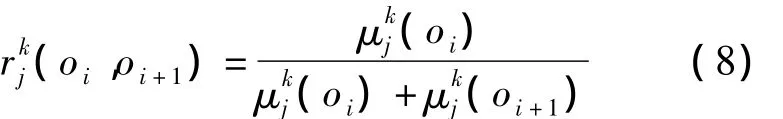
利用式(8)可以求取针对某一特征的模糊偏好矩阵，但该矩阵仅能满足互补性，不具有一致性，下面给出了一致性模糊偏好矩阵的求解方法(方法2).

①根据第k个决策者针对第j个准则给出的评价，利用上述隶属函数(式(4)～(7))计算被加工特征与各加工操作序列模糊映射的隶属度，得到

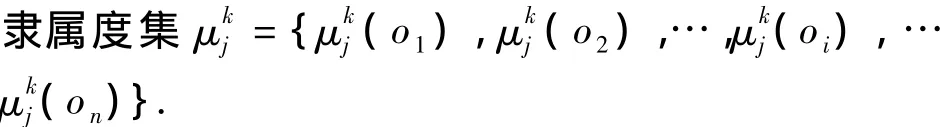
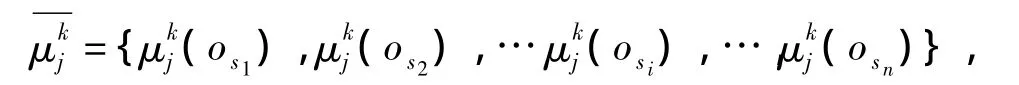
③根据式(8)，计算加工操作序列os1相对于加工操作序列osi关于第j个评估准则的二元比较模糊标度值

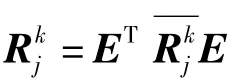
2 模糊偏好关系矩阵的集结及加工操作的选择

定义 2［15］有模糊一致矩阵 S=(sij)m×n，T=(tij)m×n，取pij=ω1sij+ ω2tij，ω1+ ω2=1，则称 P=(pij)m×n为矩阵 S=(sij)m×n和 T=(tij)m×n的合成.

定理2［15］模糊一致矩阵和的合成矩阵是模糊一致矩阵.

定理3［13］模糊偏好关系矩阵 R=(rij)n×n满足互补性，则其因素权重计算公式为

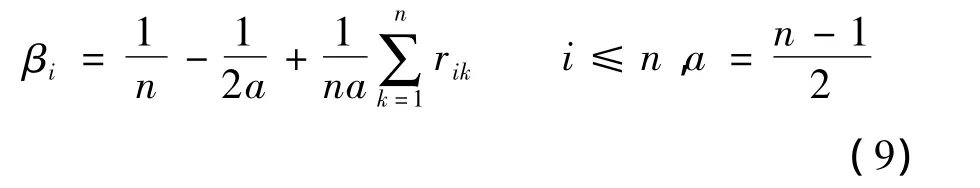
2.1 基于C-IOWA算子的多决策专家评估结果集结

如果满足以下条件，则称定义函数fj是由所产生的n维一致性IOWA算子，简记为C-IOWA算子.

条件 1［13］(k≤l)是(k≤l)中第k个元素所对应OWA对中的第2个分量，并且称〈，〉中的第1个分量为诱导分量，为数据分量的定义如下:

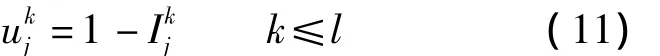
式中为专家建立的模糊偏好关系矩阵的一致性指数，它由模糊偏好关系矩阵与其自身的一致性模糊偏好关系矩阵的距离来确定，即

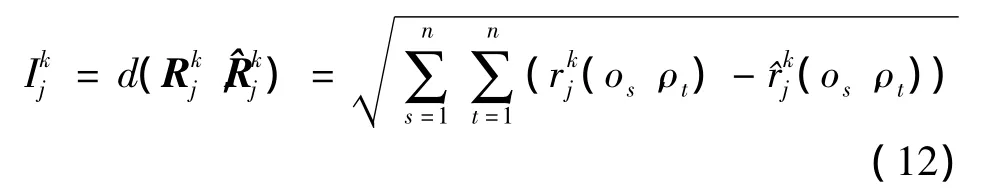
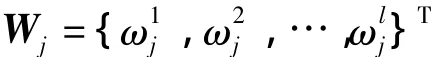
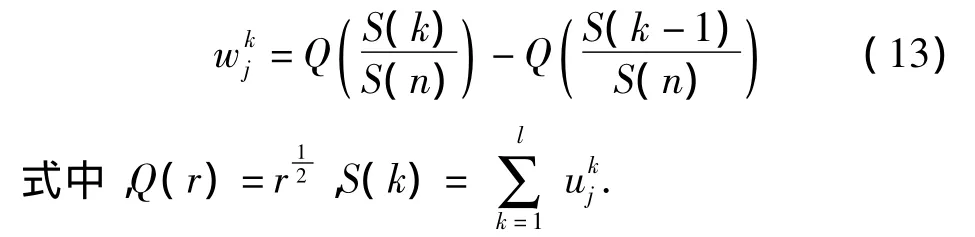
利用式(13)求得的专家权重系数，评估结果集结公式为

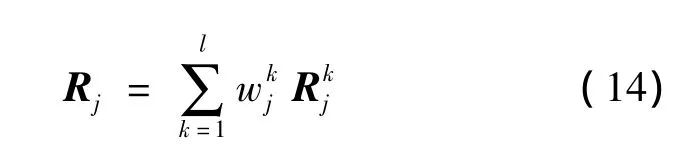
由于资深工艺师或工艺专家在经验、能力、认识等方面存在差异，他们对备选工艺方案的评价和判断不尽相同.所以针对某一评估准则，对不同资深工艺师或工艺专家的评估结果进行集结成为合理选择加工操作序列的关键所在.本文采用基于C-IOWA算子的决策者评估结果集结方法，具体过程如下(方法3):

① 利用式(12)计算各个矩阵的一致性指数，并利用式(11)，根据一致性指数求出C-IOWA集结算子的诱导分量

②利用式(13)求出各决策者的集结权重系数

③根据以上集结权重，利用式(14)得到针对第j个评估准则的集结评判矩阵Rj.

2.2 多评判准则的集结

将不同评判准则下的评判矩阵进行合成，得到集结后的评判矩阵.根据定理2可知，集结后的评判矩阵R仍是模糊一致矩阵，计算方法如下:

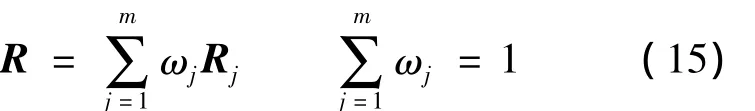
式中，ωj为相对于不同评判准则的权重系数，由工艺专家对不同评判准则重要性的评判得到，下面介绍评判准则权重系数的求解过程.

工艺专家对评估准则的重要性也给出了评价，本文将重要性分为5个等级，评估等级的重要语言集为{“不重要(UI)”，“较不重要(QUI)”，“中等(M)”，“较重要(QI)”，“重要(I)”}，采用三角模糊数表示评估等级的重要性，偏好区间如图3所示.

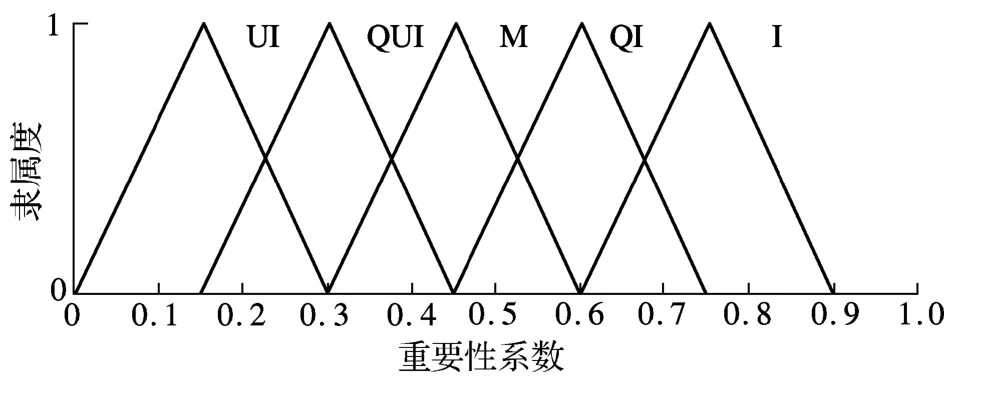
图3 工艺专家对评估准则的重要性的语义规则

不同评判准则的模糊评判矩阵的集结方法(方法4):

①根据工艺专家对评判准则重要性的评定，对评价准则的重要性进行两两比较，利用式(3)建立多个模糊偏好关系矩阵.

②根据式(2)对模糊偏好关系矩阵进行一致化处理，得到互补一致性矩阵.

③ 利用式(12)计算各个矩阵的一致性指数，并利用式(11)，根据一致性指数求出C-IOWA集结算子的诱导分量

④利用式(13)求出各决策者的集结权重系数W={w1，w2，…，wm}.

⑤根据以上集结权重，利用式(15)求解最终的模糊偏好关系矩阵R.

2.3 加工操作的选择

以上介绍了用于加工操作序列选择的基础方法，下面介绍加工操作选择的完整过程，详细过程如下(方法5):

①提取特征的尺寸精度、表面粗糙度、位置精度及形状精度等信息.

②利用方法1求取针对加工效率、加工成本及设备负载等3个评估准则的完全一致性偏好矩阵

③利用方法2求取针对尺寸精度、表面粗糙度、形状精度及位置精度等4个评估准则的完全一致性偏好矩阵

④利用方法3求取针对第j个评估准则的模糊偏好关系矩阵

⑤利用方法4求取最终的模糊偏好关系矩阵R.

⑥ 根据定理3，利用式(9)求出评判矩阵R的排序向量 D={d1，d2，…，dn}.根据向量可得到加工操作序列的排列顺序，并从备选操作序列集合O={o1，o2，…，oi，…，on}中选择合适的操作序列.

3 加工操作序列选择实例

根据某制造企业的工艺条件和工艺习惯，可将加工操作分为面腔类和孔类两类操作，详细如表1所示［7］.

加工成本的语言值集为{“非常高(EH)”，“很高(VH)”，“高(H)”，“较高(QH)”，“中等(M)”，“较低(QL)”，“低(L)”，“很低(VL)”，“非常低(EL)”}，加工效率的语言值集为{“很低(VL)”，“低(L)”，“较低(QL)”，“中等(M)”，“较高(QH)”，“高(H)”，“很高(VH)”}，设备负载的语言值集为{“很忙(VB)”，“忙(B)”，“较忙(QB)”，“中等(M)”，“较闲(QI)”，“闲(I)”，“很闲(VI)”}.由于篇幅原因，本文只给出了专家1针对孔类特征的10个加工操作序列的评估结果，如表2所示.

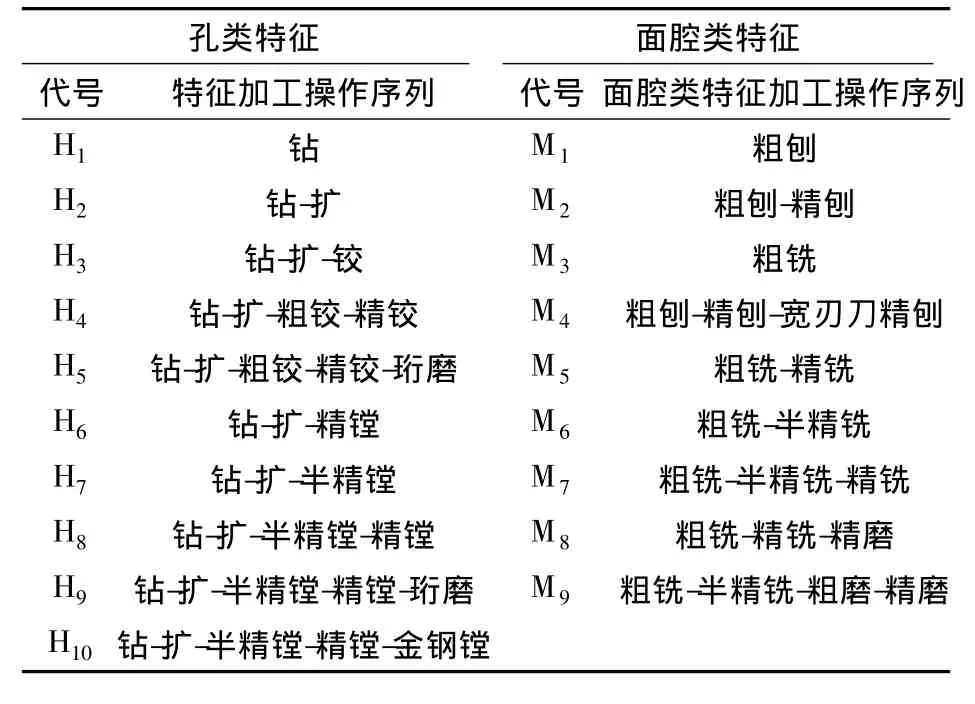
表1 孔类特征加工操作序列集合

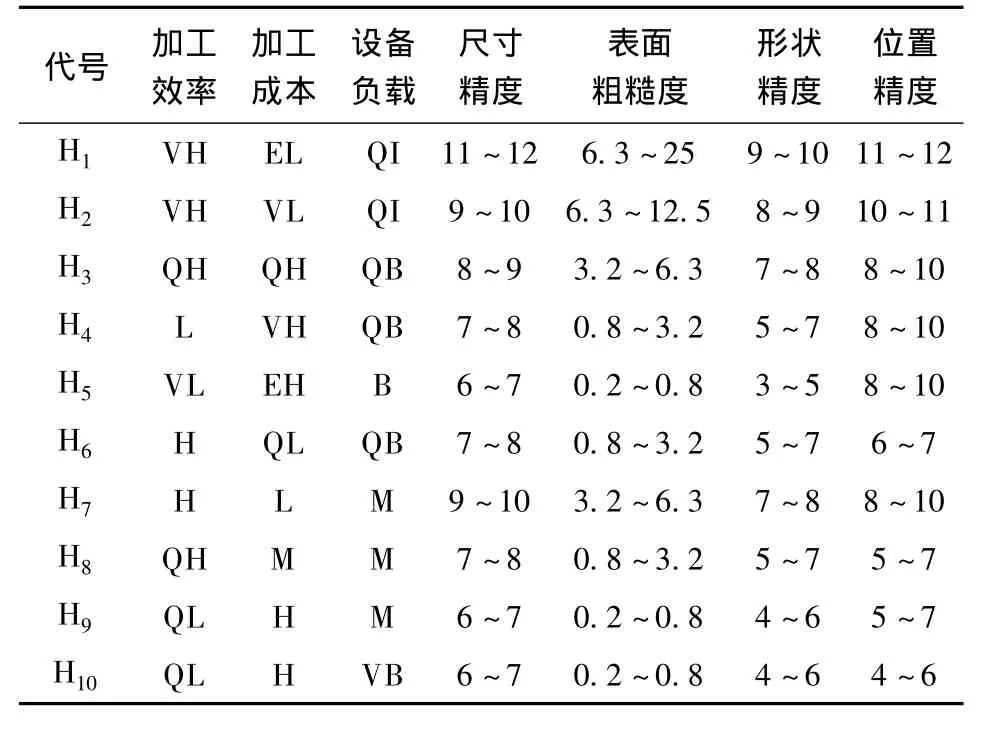
表2 专家1对孔类特征操作序列给出的评估结果

假设某一孔的尺寸精度为7，粗糙度为1.6，形状精度为6，位置精度为8，执行方法5的前5个步骤，得到集结后的评判矩阵如表3所示.

表3 集结后的评判矩阵

最后，执行方法5的第6个步骤，得到评判矩阵R的排序向量D={0.070 6，0.079 4，0.074 8，0.111 1，0.094 5，0.134 5，0.109 6，0.129 6，0.103 3，0.092 9}，由排序向量D可知，排在前3位的操作序列分别为:H6(钻-扩-精镗)，H8(钻-扩-半精镗-精镗)和 H4(钻-扩-粗铰-精铰).

4 结语

本文基于模糊偏好关系提出了用于评价和选择工艺资源的多准则群决策方法.针对不同的评判标准，将模糊偏好分成定量模糊偏好和定性模糊偏好，建立不同评判准则下的加工操作间的模糊偏好关系矩阵，提出了多专家评估结果和不同准则下评判结果的集结方法，最后根据评判矩阵的排序向量实现加工操作序列的评价和选择.本文提出的工艺资源评价和选择方法充分考虑了评判准则的多样性和领域专家间的差异性，较好地克服了工艺资源选择过程中随意性强和对工艺人员经验依赖大等不足，增强了工艺设计过程中的智能化和自动化，提高了工艺设计的效率.最后通过算例实现了基于模糊偏好关系的工艺资源评价与选择的多准则群决策方法的应用，验证了该方法的科学性和适用性.

［1］Garcia J M T，del Moral M J，Martinez M A，et al.A consensus model for group decision making problems with linguistic interval fuzzy preference relations［J］.Expert Systems with Applications，2012，39(11):10022-10030.

［2］Ertay T，Kahveci A，Tabanl R M.An integrated multicriteria group decision-making approach to efficient supplier selection and clustering using fuzzy preference relations［J］.International Journal of Computer Integrated Manufacturing，2011，24(12):1152-1167.

［3］Amindoust A，Ahmeda S，Saghafiniab A，et al.Sustainable supplier selection:a ranking model based on fuzzy inference system［J］.Applied Soft Computing，2012，12(6):1668-1677.

［4］Chen Y H，Chao R J.Supplier selection using consistent fuzzy preference relations［J］.Expert Systems with Applications，2012，39(3):3233-3240.

［5］Wu D D.Performance evaluation:an integrated method using data envelopment analysis and fuzzy preference relations［J］.European Journal of Operational Research，2009，194(1):227-235.

［6］Deb S，Ghosh K，Paul S.A neural network based methodology for machining operations selection in computer-aided process planning for rotationally symmetrical parts［J］.Journal of Intelligent Manufacturing，2006，17(5):557-569.

［7］秦宝荣.智能CAPP系统的关键技术研究［D］.南京:南京航空航天大学机电学院，2003.

［8］肖九一，李双跃，郭春香.基于偏好关系的制造工艺资源评价与选择的模糊决策方法［J］.模糊系统与数学，2008，22(5):95-100.

Xiao Jiuyi，Li Shuangyue，Guo Chunxiang.The evaluating and selecting of manufacturing process resource based on preference relation［J］.Fuzzy System and Mathematics，2008，22(5):95-100.(in Chinese)

［9］Radwan A.A practical approach to a process planning expert system for manufacturing processes［J］.Journal of Intelligent Manufacturing，2000，11(1):75-84.

［10］Jiang Bing，Lau Henry，Chan Felix T S，et al.An automatic process planning system for the quick generation of manufacturing process plans directly from CAD drawings［J］.Journal of Materials Processing Technology，1999，87(1/2/3):97-106.

［11］杨莉，李南，和媛媛.三角模糊数互补判断矩阵的加性一致性及排序［J］.系统工程，2009，27(3):89-92.

Yang Li，Li Nan，He Yuanyuan.Additive consistency and prioritization for triangular fuzzy number complementary judgment matrix［J］.Systems Engineering，2009，27(3):89-92.(in Chinese)

［12］张细香，刘建勋，雷静，等.模糊互补矩阵的加性一致性阈值仿真［J］.计算机仿真，2010，27(1):316-318，333.

Zhang Xixiang，Liu Jianxun，Lei Jing，et al.The approximate threshold of additive consistency index for fuzzy complementary matrix［J］.Computer Simulation，2010，27(1):316-318，333.(in Chinese)

［13］王雪青，邴兴国，李海丽.基于模糊偏好关系的工程项目方案优选方法研究［J］.科技进步与对策，2008，25(10):91-93.

［14］张旭.决策信息不明确的多目标模糊优化模型与方法［D］.大连:大连理工大学机械工程学院，2009.

［15］周文坤，武振业，刘家诚.模糊偏好条件下多目标群决策的方法［J］.西南交通大学学报，2001，36(3):232-234.

Zhou Wenkun，Wu Zhenye，Liu Jiacheng.Multi-attribute group decision-making method under fuzzy preferences［J］.Journal of Southwest Jiaotong University，2001，36(3):232-234.(in Chinese)

Multi-criteria and multi-experts decision-making method for process resource evaluation and selection based on fuzzy preference relation

Liu Xiaojun Ni Zhonghua Yang Zhangqun

(School of Mechanical Engineering，Southeast University，Nanjing 211189，China)
(Jiangsu Key Laboratory for Design and Manufacture of Micro-Nano Biomedical Instruments，Southeast University，Nanjing 211189，China)

Abstract:Taking the selection process of a machining operation sequence for example，the multi-criteria and multi-experts decision-making method for process resource evaluation and selection based on fuzzy preference relations is proposed.The fuzzy preference relations for different assessment criteria，such as processing efficiency，processing costs，equipment load，dimensional accuracy，surface roughness，form accuracy and position accuracy，are divided into quantitative fuzzy preference and qualitative fuzzy preference.The quantitative depiction of qualitative fuzzy preference criteria is given，and the function for quantitative fuzzy preferences criteria membership is established.Based on the C-IOWA，the aggregate method of the fuzzy preference relation matrices for multi-criteria and multi-experts assessment results is studied，which is used to obtain the consistency fuzzy preference matrix.Then，the method for computing the priority weight vector，which is used as the evaluation and selection criteria，is given.Finally，an example is used to verify the validity of the proposed method.

Key words:process resource selection;fuzzy preference relations;multi-criteria and multi-experts decision making;quantitative;membership function

中图分类号:TH16

A

1001－0505(2014)01-0063-07

doi:10.3969/j.issn.1001 －0505.2014.01.012

收稿日期:2013-06-20.

刘晓军(1980—)，男，博士，讲师，liuxiaojun@seu.eud.cn.

基金项目:某部预研资助项目(513180102，51318010103)、某部预研重点基金资助项目(9140A18010111JW0602)、教育部青年基金资助项目(10YJC880109).

刘晓军，倪中华，杨章群.基于模糊偏好关系的工艺资源评价与选择的多准则群决策方法［J］.东南大学学报:自然科学版，2014，44(1):63-69.［doi:10.3969/j.issn.1001 －0505.2014.01.012］