基于滑模变结构的高超声速飞行器控制律设计

刘涛, 闫斌斌, 顾文娟, 于云峰

(西北工业大学 航天学院, 陕西 西安 710072)

0 引言

高超声速飞行器具有重要的军事意义和战略价值,近年来成为国内外研究的热点[1]。由于高超声速飞行器采用机体推进一体化结构设计,飞行速度很快,处于高动压飞行条件下,且飞行距离远,使得飞行器模型的参数不确定性和外部干扰十分显著,因此其控制问题一直是研究难点。高超声速飞行器控制系统必须对参数摄动和外部干扰具有强鲁棒性。文献[2]针对线性化模型,设计了两种基于线性二次调节器技术的控制器,虽然设计的控制律在一定巡航条件下是有效的,但是需要增加增益调度环节,这就增加了设计复杂性。文献[3]提出了一种基于近似反馈线性化的非线性控制设计方法,尽管对大量包线可以实现稳定跟踪,但是由于控制律设计过于复杂,因此难以对其稳定性和鲁棒性能进行解析分析。

本文针对高超声速飞行器纵向模型,首先在平衡状态建立一个线性模型,然后通过设计一个参考模型构造出一个误差跟踪模型。进而设计一个鲁棒滑动面以及自适应滑模控制器,使得跟踪误差在有限时间内进入预设滑动面,以保证模型存在参数不确定和外部干扰时的渐进稳定性和对控制输入的精确跟踪。

1 高超声速飞行器纵向运动数学模型

1.1 数学模型描述

文中的高超声速飞行器纵向模型采用文献[3]中的设计,模型方程组在此不再赘述。

将非线性方程组在平衡点(x0,u0)处泰勒展开,只保留一阶项,可以得到状态空间形式的线性模型:

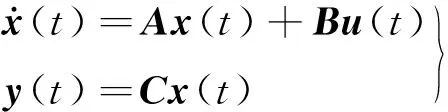
(1)

式中,x(t)=[V,μ,h,α,q]T为状态变量;u(t)=[φ,δe]T为控制输入;y(t)=[h,V]T为输出向量。

由于飞行器模型存在时变的参数不确定和干扰,因此需要考虑包含参数不确定和干扰的系统为[4]:

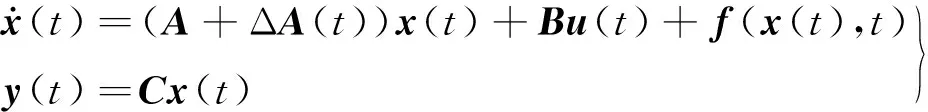
(2)

式中,ΔA(t)为矩阵A的参数摄动矩阵;f(x(t),t)为一个未知的外部干扰非线性函数。上述不确定系统的参考模型选取如下[5]:

(3)

式中,xm(t)为参考模型的状态;Am和Bm为实常矩阵,假设Am稳定;r(t)为参考模型的输入。

模型参考控制系统的跟踪误差向量定义为:

e(t)=x(t)-xm(t)

(4)

由上述式(2)～式(4)推导出误差模型为:

Am)x(t)+f(x(t),t)-Bmr(t)

=Ame(t)+Bu(t)+(A-Am)x(t)-

Bmr(t)+ΔA(t)x(t)+f(x(t),t)

(5)

其标称模型为:

1.2 参考模型设计

构造的参考模型满足完全跟踪的模型匹配条件:

因此,需要对参考模型进行设计,使其满足完全跟踪的条件。此外,参考模型的设计还应保证模型具有一定的动态品质,且保证(Am,B)为完全可控对。

假设希望的参考模型的特征多项式为:

D(s)=sn+an-1sn-1+…+a1s1+a0

根据上式及完全跟踪的模型匹配条件,取

式中,P为非奇异变换阵;Km∈{K∈Rm×l,rank(K)=l}。

2 滑模变结构模型参考控制系统设计

滑模变结构模型参考控制系统设计包括:设计滑模参数矩阵,以保证滑动模态运动稳定且具有良好的动态品质;构造滑模变结构控制律,以保证系统到达滑动模态并且不脱离滑动模态[6]。

2.1 滑动模态参数矩阵设计

针对式(5)描述的误差模型,选取全程滑动模态切换超平面:

S(e,t)=Ce(t)

(6)

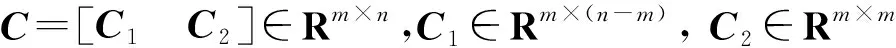
由标称系统和S(e,t)=Ce(t),则有:

令S=Ce=0,解得:e2=-Ke1。则误差的滑动模态运动方程为:

(7)

式中,K=C2-1C1。

由于(Am,B)为完全可控对,则(Am,11,Am,12)也为完全可控对。选择K使(Am,11-Am,12K)的特征根为系统希望的特征根,从而保证系统在滑动阶段具有良好的动态品质。取C2为单位矩阵,则有:

2.2 滑模变结构控制律设计

构造滑模变结构控制律为:

u=um+uv

(8)

式中,um为模型参考控制系统的匹配控制律;uv为变结构控制律。

根据完全跟踪的模型匹配条件,考虑误差的标称模型为:

则匹配控制律设计为:

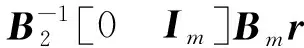
(9)

将上式代入完整误差模型,则有:

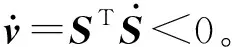
uv=-g(t)(CB)-1sgn(S)

(10)

式中,g(t)为待求的标量控制系数。此时:

ΔA(t)x(t)+f(x(t),t)]

=-g(t)STsgn(S)+STC[Ame(t)+

ΔA(t)x(t)+f(x(t),t)]

≤ -g(t)‖ST‖+‖ST‖[‖CAm‖‖e‖+

φa‖C‖‖x‖+φf‖C‖]

g(t)= ‖CAm‖‖e‖+φa‖C‖‖x‖+

φf‖C‖+ε

(11)

式中,ε为一个小的正常数。

颤振是滑模控制系统的常见现象[7]。为了减弱通常由滑模控制器方程式(10)中的sgn(S)引起的颤振现象,本文采用一种简单实用的消颤方法,即用M(S)代替sgn(S),则

式中,δi为一个小的正常数。

综合式(8)～式(11),构造的滑模变结构控制律为:

[‖CAm‖‖e‖+φa‖C‖‖x‖+

φf‖C‖+ε](CB)-1M(S)

(12)

3 仿真结果及分析

仿真采用文献[8]中的模型参数,模型的初始平衡状态参数为:h=30 km,v=3 026.5 m/s,α=0.105 59°,μ=0°,q=0,φ=0.058 4(无量纲),δe=-10.802°。基于2.1节中飞行器纵向模型的设计方法,获得线性模型如下:

高超声速飞行器的飞行过程中存在气动参数摄动和外部干扰。假定不确定参数在标称值40%以内变动,外部干扰是有界的,可以被看作为阵风[9],本文选取f(x(t),t)=[sint,0.3 sint,2,5 cost,0.5 sint]T。

仿真的控制目标是验证飞行器能否精确跟踪指令速度和指令高度。选择通过滤波器的阶跃输入作为参考模型的输入,取速度和高度增量分别为500 m/s和5000 m,即要求速度和高度跟踪阶跃变化。每个指令均通过一个滤波器:

式中,阻尼比ξ=0.95,ωn=0.05 rad/s。速度和高度跟踪结果如图1所示。

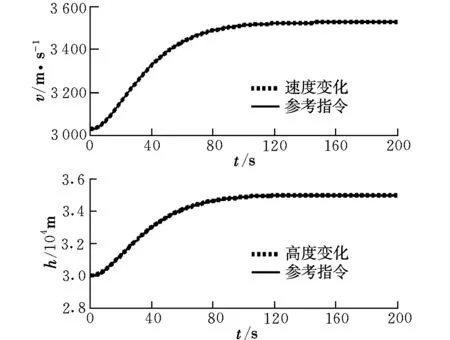
图1 速度和高度跟踪曲线Fig.1 Curves for speed and height tracking

迎角和飞行航迹角变化如图2所示。从图2可以看出,迎角和飞行航迹角响应良好。

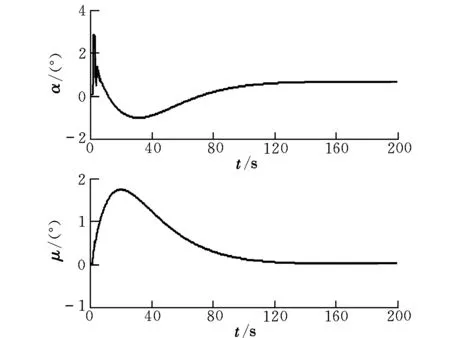
图2 迎角和飞行航迹角变化曲线Fig.2 Curves for AOA and flight path angle

燃空比和升降舵为系统控制输入,二者的响应曲线如图3所示。从图3可以看出,控制器的控制响应时间和收敛速度都比较快。

图3 燃空比和舵偏角响应曲线Fig.3 Response curves for fuel-air ratio and elevator deflection

通过以上仿真结果可知,高超声速飞行器的速度和高度可以快速、精确跟踪指令要求,跟踪误差很小,具有良好的鲁棒性能。这表明,设计的控制方法可以有效解决高超声速飞行器存在的气动参数摄动和外部干扰问题。

4 结束语

考虑高超声速飞行器的气动参数摄动和外部干扰因素,根据线性模型设计了参考模型和滑模变结构模型参考控制系统,并通过李雅普诺夫稳定性定理验证其稳定性。数字仿真结果表明,速度和高度可以快速、精确跟踪指令要求,具有良好的鲁棒性能,说明所设计的滑模变结构模型参考控制系统可以有效解决高超声速飞行器存在的气动参数摄动和外部干扰问题。

参考文献：

[1] Bolender M A.An overview on dynamics and controls modelling of hypersonic vehicles[C]//American Control Conference,2009(ACC’09).IEEE,2009:2507-2512.

[2] Groves K P,Sigthorsson D O,Serrani A,et al.Reference command tracking for a linearized model of an air-breathing hypersonic vehicle [R].AIAA-2005-6144,2005.

[3] Parker J,Serrani A,Yurkovich S,et al.Control-oriented modeling of an air-breathing hypersonic vehicle [J].Journal of Guidance,Control,and Dynamics,2007,30 (3):856-869.

[4] Buschek H,Calise A.Uncertainty modeling and fixed-order controller design for a hypersonic vehicle model [J].Journal of Guidance,Control,and Dynamics,1997,20 (1):42-48.

[5] Choi H.Variable structure control of dynamical systems with mismatched norm-bounded uncertainties: an LMI approach [J].International Journal of Control,2001,74 (13):1324-1334.

[6] 李言俊,张科.自适应控制理论及应用[M].西安:西北工业大学出版社,2005:157-176.

[7] Hung J,Gao W,Hung J.Variable structure control: a survey [J].IEEE Transactions on Industrial Electronics,1993,40(1):2-22.

[8] Clark A,Wu C,Mirmirani M.Development of an airframe propulsion integrated generic hypersonic vehicle model[C]//The 44th AIAA Aerospace Sciences Meeting and Exhibit.Reno:AIAA,2006:206-218.

[9] Gibson T,Crespo L,Annaswamy A.Adaptive control of hypersonic vehicles in the presence of modeling uncertainties[C]//American Control Conference,2009(ACC’09).IEEE,2009:3178-3183.