恶意代码的函数调用图相似性分析

2014-09-15刘星，唐勇

计算机工程与科学 2014年3期

关键词：函数调用调用相似性

刘星，唐勇

(国防科学技术大学计算机学院，湖南长沙 410073)

恶意代码的函数调用图相似性分析

刘星，唐勇

(国防科学技术大学计算机学院，湖南长沙 410073)

恶意代码的相似性分析是当前恶意代码自动分析的重要部分。提出了一种基于函数调用图的恶意代码相似性分析方法，通过函数调用图的相似性距离SDMFG来度量两个恶意代码函数调用图的相似性，进而分析得到恶意代码的相似性，提高了恶意代码相似性分析的准确性，为恶意代码的同源及演化特性分析研究与恶意代码的检测和防范提供了有力支持。

恶意代码；函数调用图；图的相似性距离；指令序列；最大权匹配

1 引言

恶意代码分析是检测和防范恶意代码的重要基础。随着基于蜜罐技术的恶意代码自动捕获器及大量恶意代码样本上传网站的建立，恶意代码样本的捕获已不存在技术困难，关键问题是如何对数量呈海量化趋势的恶意代码样本进行自动、及时和准确的分析。

恶意代码的相似性分析是当前恶意代码自动分析的重要部分。现有的恶意代码相似性分析方法要么过多地关注于恶意代码的byte级特征，如Kolter J Z和Maloof M A[1]提出用byte代码的n-gram作为特征对恶意代码进行分类；要么过于关注恶意代码的函数调用图的结构，比如文献[2]提出了一种用图的编辑距离来度量两个恶意代码函数调用图的相似性的分析方法。

鉴于这些方法的缺陷和不足，本文提出了一种用图的相似性距离来度量两个恶意代码函数调用图的相似性的分析方法，该方法考虑了恶意代码中函数的指令级信息以及函数之间的调用关系信息。

文章组织结构如下：第2节是文章的主要内容，2.1节介绍了函数调用图的相似性距离的定义， 2.2节是完全二分图的构建方法，2.3节是完全二分图的边权矩阵的计算方法，2.4节是二分图的最大权匹配的计算方法以及两个函数调用图相似性距离SDMFG(Similar Distance of Malware Function-call Graphs)的计算方法;第3节是实验部分;第4节是文章总结。

2 图的相似性分析

2.1 函数调用图的相似性距离

首先给出恶意代码函数调用图的相似性距离SDMFG的定义。

定义1 (SDMFG)设图G和H是两个恶意代码函数调用图，图G和H间所有匹配路径中匹配成本最小的匹配路径，称为图G和H的最优匹配路径，这个最优匹配路径的匹配成本就是两个恶意代码函数调用图G和H的相似性距离SDMFG。

这里，图G和H之间的一个匹配路径是指由G转化为H所需的所有顶点匹配操作。顶点的匹配操作包括匹配两个点、删除一个点和插入一个点三种。只有当两点所对应的函数很相似且它们的调用函数序列也很相似时才会进行匹配操作，而对G中其余点做删除操作，对H中其余点做插入操作。如G由点x1和x2构成，而H由y1构成，则G和H之间有三条匹配路径：

(1)点x1匹配点y1，删除点x2；

(2)点x2匹配点y1，删除点x1；

(3)删除点x1和点x2，插入点y1。

每个匹配操作σ都有一个成本，即匹配成本c(σi)，依操作类型分为三类：匹配点成本、删除点成本和插入点成本。我们从两个方面来考虑两个点是否匹配：两点所对应的函数的相似性以及两点的邻接边所对应的调用关系的相似性。两点所对应的函数越相似，两点的匹配成本越小，两点也就越相匹配；两点所对应函数的调用函数序列越相似，两点的匹配成本也越小，两点也就越相匹配；若有两个点与另一个点所对应的函数相似性相同时，则它们之中与另一点所对应的函数调用关系越相似的那个点与另一个点更匹配。

完全相同的两个点的匹配成本c(σi)=0，完全不同的两个点的匹配成本c(σi)=1；插入一个点和删除一个点的成本很高，接近于1。一条匹配路径的匹配成本就是构成这条路径的所有得到顶点匹配操作的匹配成本之和。由于恶意代码函数调用图的相似性距离SDMFG被定义为两图间最优匹配路径的成本，恶意代码函数调用图的相似性问题就转换成了求两图的最小成本匹配问题。

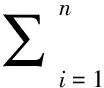
(1)

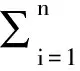
因此，恶意代码函数调用图的相似性问题就转换成了求最大权匹配问题，可以通过Kuhn-Munkres算法[3,4]解决。下面介绍通过求最大权匹配来求恶意代码函数调用图的SDMFG值的过程。

2.2 构造完全二分图

求最大权匹配问题可以通过Kuhn-Munkres算法[3,4]来解决。首先，利用两个恶意代码函数调用图G1和G2构造一个完全二分图G；然后，计算该二分图的边权矩阵C；接着，利用Kuhn-Munkres算法计算该二分图的最大权匹配M；最后，根据M计算恶意代码函数调用图的相似性距离。

根据两个恶意代码函数调用图的函数调用信息构造一个完全二分图的算法如算法1所示。其中，函数调用信息是用反汇编工具提取并以邻接矩阵的形式存放的。

算法1 构造完全二分图

输入：两个恶意代码函数调用图G1和G2的函数调用信息；

输出：完全二分图G=(X∪Y,E)；

步骤1 根据两个恶意代码函数调用图的函数调用信息,分别提取两个函数调用图G1的顶点集V1和G2的顶点集V2；把G1的顶点集V1加入到X中，把G2的顶点集V2加入到Y中。

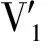
步骤3 根据步骤1和步骤2计算得到的图的顶点集V=X∪Y，对X中任一点和Y中任一点之间都加上一条边，构造二分图的边集；对所有边都进行加权就得到了一个|X|*|Y|的边权矩阵C。

2.3 计算二分图的边权矩阵

对一个完全二分图的边权的选择是图比对算法的核心部分之一，因为它表述了两个比对图的信息，是图比对算法的输入前提，对边权选择得越好，图比对算法的结果就越接近实际情况。边权矩阵中元素的值是通过计算权衡函数的相似性和函数调用关系的相似性得到的。下面，我们先计算函数的相似性和函数调用关系的相似性，然后计算边权矩阵。

2.3.1 计算函数的相似性

函数的相似性是通过求用IDA工具提取的函数指令助记符序列最佳匹配，并计算最佳匹配情况下所有指令中匹配指令所占百分比得到的。

算法2 计算函数的相似性

输入：函数调用图G1中函数v1和图G2中函数v2；

输出：函数v1和v2的相似性。

步骤1 用反汇编工具IDA提取函数v1和v2的指令助记符序列S1和S2，若提取函数v1或v2的指令助记符序列不成功，那么记两个函数的相似性分数Sf=0。

步骤2 运用生物信息学中的双序列比对算法Needleman-Wunsch[5]做全局序列比对，找到两个序列S1和S2之间的最佳匹配。

步骤1 把匹配数在所有指令助词符数中所占得的百分比作为两个函数v1和v2的相似性分数。

例如，两个函数指令助记符序列S1=(push, push, call, push, mov, add, push, push, call, retn)，S2=(push, mov, call, test, jz, push, call, pop, mov, pop, retn)，则最佳Needleman-Wunsch匹配结果如图1所示。

Figure 1 The best matching between sequences S1 and S2图1 S1和S2序列的最佳匹配

显而得之，S1和S2两个序列只有3个指令助记符是匹配的，在S1序列中插入了一个空格，且有7个指令助记符是不匹配的，总的指令助词符数是11。所以两函数的相似性Sf=3/11。

2.3.2 计算函数调用关系的相似性

一般来说，如果两个函数相似的话，那么这两个函数的指令序列肯定在很大程度上也是很相似的，因此，当两个函数的指令序列的相似性达到一定程度时，就可以判定这两个函数是相似的。在生物信息学中已有大量研究表明，当DNA或氨基酸序列的相似性达到一定程度时，一般就可以判定两个序列是相似序列。

如果根据2.3.1小节中的方法来计算指令序列的相似性，那么当函数的指令序列的相似性达到一定程度时就可以判断两个函数是相似的。通过大量实验可以得出结论，只要指令序列的相似性达到50%，就可以判断两个函数是相似的。

当然，如果同时有两个函数的指令序列与某个函数的指令序列的相似性都很高，那么，为了保证函数调用图中各个函数的一对一匹配，则取与之相似性最大的那个函数作为这个函数的相似函数。两个相似函数称为一个相似函数对。

两个函数的调用关系的相似性是指这两个函数的调用函数和被调用函数中相似函数对所占的比例。算法如下所示：

算法3 计算函数调用关系的相似性

输入：函数调用图G1中函数v1和图G2中函数v2的调用函数集和被调用函数集，图G1中任意函数x与G2中任意函数y的相似性；

输出：函数v1与函数v2的调用关系的相似性。

步骤1 计算函数v1调用的函数(即调用函数)和函数v2调用的函数所构成的相似函数对的数量N1，计算调用函数v1的函数(即被调用函数)和调用函数v2的函数所构成的相似函数对的数量N2；

步骤2 计算函数v1的调用函数和被调用函数中不与函数v2的任何调用函数及被调用函数相似的数量N3，计算函数v2的调用函数和被调用函数中不与函数v1的任何调用函数及被调用函数相似的数量N4；

步骤3 以N1+N2+N3+N4作为总数，并以相似函数对的数量N1+N2在其中所占的比例作为两个函数v1和v2的调用关系的相似性分数Se，即Se=(N1+N2)/(N1+N2+N3+N4)。

2.3.3 计算边权矩阵

在文献[6]中，匹配任何两个实节点的成本都被简单地定义为重标成本。而在文献[2]中，将匹配任何两个实节点的成本定义为重标成本与邻居成本之和。它们都没有考虑函数内部信息(如指令序列)的相似性，匹配结果精确性太低。本文提出如下加权算法：

算法4 计算边权矩阵

输入：完全二分图G=(X∪Y,E)，X中任一顶点所对应函数v1和Y中任一顶点所对应函数v2的相似性及其调用关系的相似性；

输出：二分图G的边权矩阵C。

步骤1 若函数v1和函数v2都是实节点，则它们对应的边的权值为:

C(v1,v2)=[Sf(v1,v2)+Se(v1,v2)]/2

(2)

步骤2 若函数v1和函数v2两者之中有一个是虚节点或者都是虚节点，则它们对应的边的权值C(v1,v2)=0.1(这意味着它们所对应的点是插入或者删除操作)。

2.4 求最大权匹配和两图的相似性距离

得到了完全二分图G的边权矩阵C之后，利用Kuhn-Munkres算法在完全二分图的C上求最大权匹配M。然后根据二分图的最大权匹配M求两个恶意代码函数调用图的相似性距离SDMFG，计算算法如下。

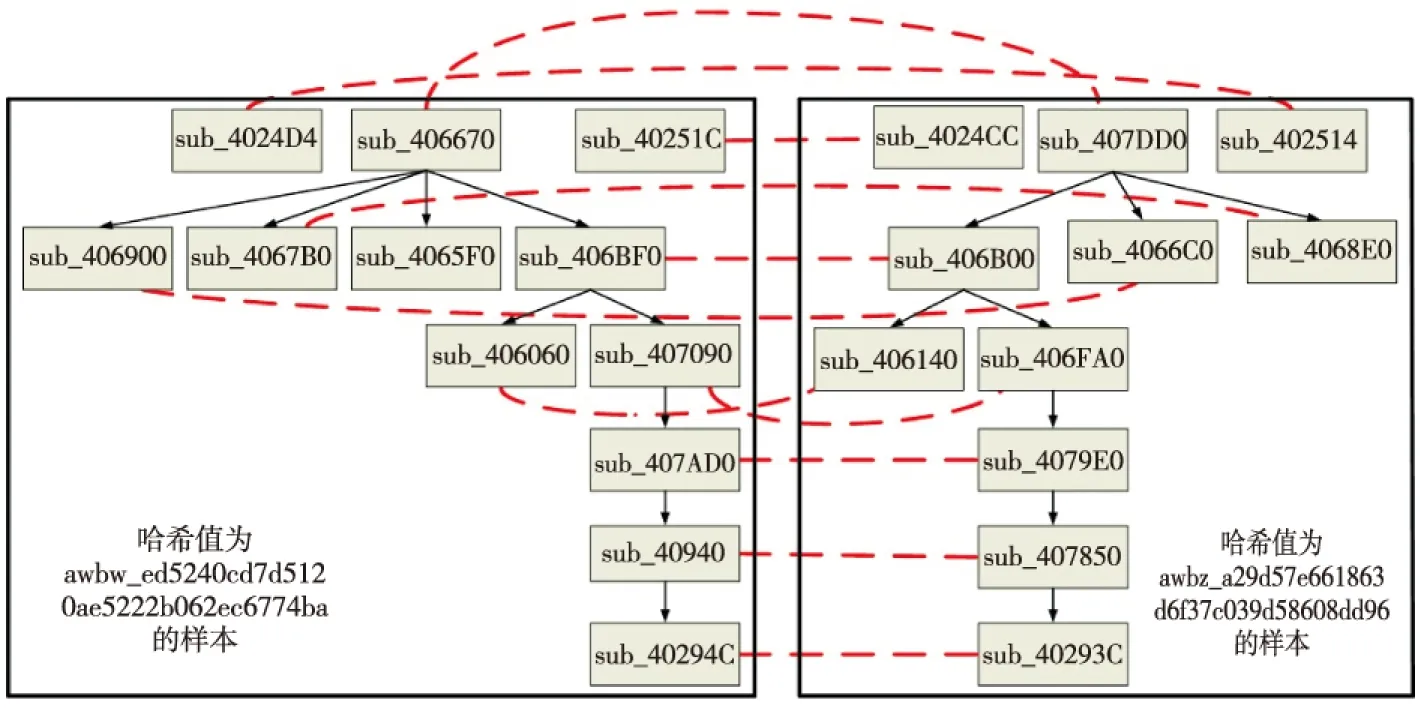
Figure 2 The result of SDMFG algorithm图2 SDMFG方法结果

算法5 求最大权匹配算法

输入：完全二分图G的最大权匹配M及其权值w；

输出：两个恶意代码函数调用图G1和G2的相似性距离SDMFG。

步骤1 找出M中的实节点与实节点的匹配边(匹配点操作)、实节点与虚节点的匹配边(删除点或插入点操作)和虚节点与虚节点的匹配边(非匹配操作)，并分别计算它们数量以及二分图的一个划分的点数n(这里n的含义同上文)；

步骤2M中的实节点与实节点的匹配边(匹配点操作)、实节点与虚节点的匹配边(删除点或插入点操作)构成了G1和G2的最优匹配路径，它们匹配成本就是G1和G2的相似性距离。设虚节点与虚节点的匹配边的数量为n1，则两个恶意代码函数调用图G1和G2的相似性距离SDMFG=(n-w)-n1*(1-0.1)。

3 实验结果

本节应用SDMFG算法对恶意代码的函数调用图进行相似性比对，并评估方法的性能与效率。整个方法是在Windows XP系统上用VC实现的。

3.1 比较SDMFG方法和文献[2]方法的准确性

对两个哈希值分别为awbw_ed5240cd7d5120ae5222b062ec6774ba和awbz_a29d57e661863d6f37c039d58608dd96的样本，用两种方法做函数调用图相似性分析的结果分别如图2和图3所示，两个小框中分别是两个函数调用图，匹配的函数点用虚线连接(由于篇幅的原因，图中没有画出被调用的库函数，所以匹配的两个函数的调用函数数量在图中看起来不一样)。很明显，在图2中函数sub_4024D4匹配sub_402514，在图3中却是函数sub_4065F0匹配sub_402514。由于三个函数sub_4024D4、sub_4065F0和sub_402514都无法提取到函数的指令助记符序列，故函数sub_4024D4与sub_402514、函数sub_4065F0与sub_402514的相似性分数均为Sf=0，两组函数对的顶点重标成本也均为1，这时只能通过比较函数sub_4024D4与sub_402514的调用关系相似性(出入度邻接成本)以及函数sub_4065F0与sub_402514的调用关系相似性(出入度邻接成本)来判断哪一组函数对相匹配更贴近实际情况。然而，函数sub_4024D4和sub_402514都只调用了库函数(且都只调用了同一个库函数DllFunctionCall)，但是函数sub_4065F0却被函数sub_40-6670调用(且调用了一个不同的库函数——vbaFreeVar)，即函数sub_4024D4与sub_402514的调用关系相似性(值为1)比函数sub_4065F0与sub_402514的调用关系相似性(值为0)要大，且前一组函数对的出入度邻接成本(值为0)比后一组函数对的(值为1)要小。这里文献[2]方法给出了错误的结果，因为在求最大权匹配M时，sub_4065F0与sub_402514匹配可以使得M的权值最大，即使sub_4065F0与sub_402514并不应该相匹配。显然，文献[2]方法的准确性没有本文方法好。

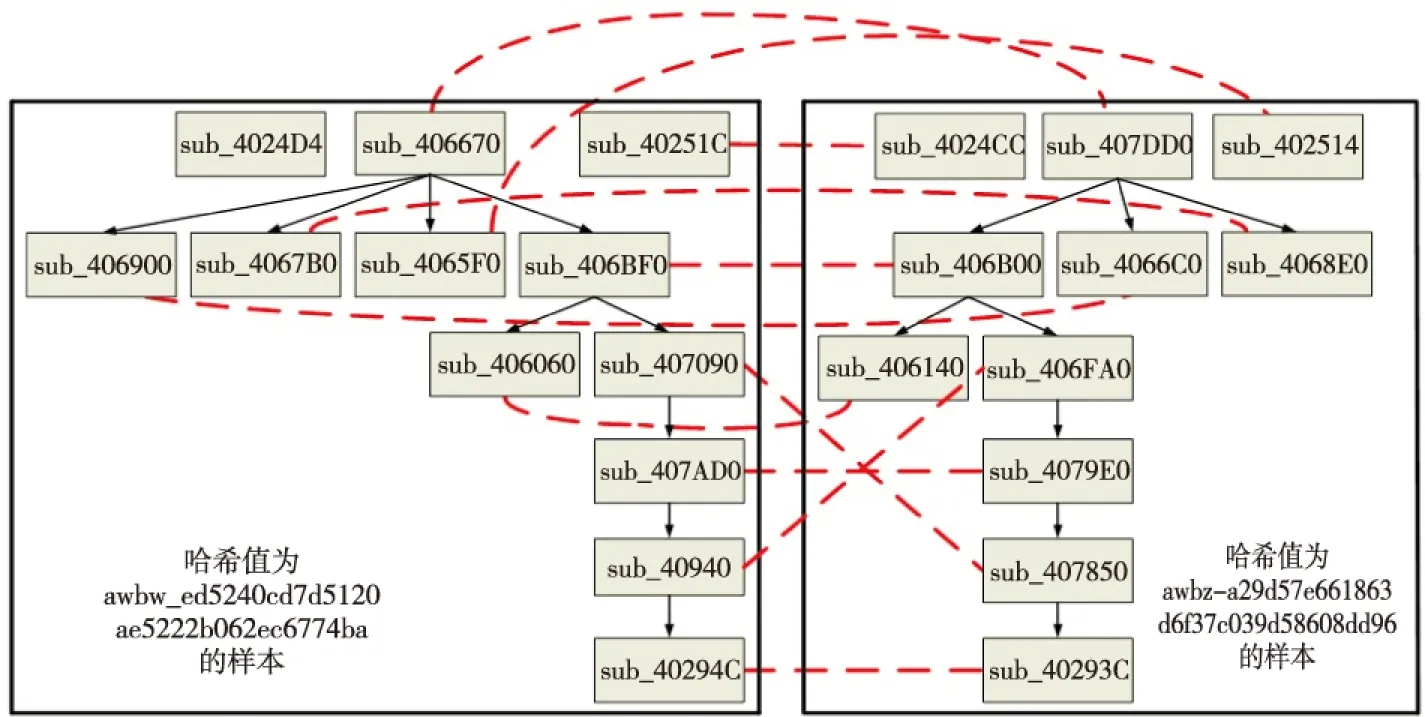
Figure 3 The result of reference[2] algorithm图3 文献[2]方法结果

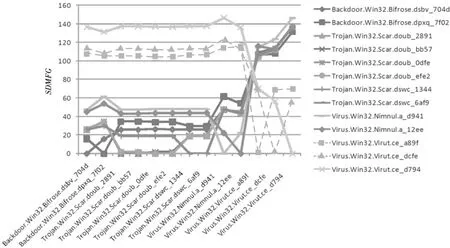
Figure 4 Similar distance of malware function-call graphs图4 恶意代码的相似性距离

3.2 比较SDMFG方法和文献[2]方法的效率

假设两个比对图的顶点集平均大小为t，则本文中构建二分图的时间复杂度是O(2t)。假设两个函数的指令助记符序列平均长度为l，计算所有函数对的指令助记符序列相似性的时间复杂度是O(t2*l2)。假设两个函数的调用和被调用函数个数平均为m，计算所有函数对的调用关系相似性的时间复杂度是O(t2*m2)。计算加权矩阵的时间复杂度是O((2t)2)。用Kuhn-Munkres算法求二分图的最大权匹配的时间复杂度是O((2t)3)。所以,SDMFG方法的时间复杂度总和是O(2t+t2*l2+t2*m2+(2t)2+(2t)3)。文献[2]中，构建二分图的时间复杂度是O(2t)，计算重标成本的时间复杂度是O((2t)2),计算邻居成本的时间复杂度是O(t2*m2),计算加权矩阵的时间复杂度是O((2t)2),用Kuhn-Munkres算法求二分图的最大权匹配的时间复杂度是O((2t)3)。所以,文献[2]方法的时间复杂度总和是O(2t+t2+t2*m2+(2t)2+(2t)3)。很容易就能发现，两种方法的时间复杂度的区别主要在于计算所有函数对的指令助记符序列相似性和计算重标成本，前者要比后者大，所以后者效率要稍高些。

3.3 一组恶意代码样本的函数调用图相似性分析

任取2个Backdoor.Win32.Bifrose样本、6个Trojan.Win32.Scar样本、2个Virus.Win32.Nimnul样本和3个Virus.Win32.Virut样本进行恶意代码函数调用图相似性分析，它们的图相似性距离SDMFG结果如图4所示。图4横轴是各个样本，纵轴表示样本与样本之间的函数调用图相似性距离，即SDMFG值，每条曲线都表示一个恶意代码样本与其它所有样本的函数调用图的相似性距离。可以很容易看出，同一恶意代码的样本之间的SDMFG值比较小且相差不大，而它们与其他恶意代码的样本之间的SDMFG值则要比较大，而且与不同恶意代码的样本之间的SDMFG值相差较大。

4 结束语

恶意代码的相似性分析是当前恶意代码自动分析的重要部分之一。本文利用生物信息学中的序列比对方法计算函数的相似性，并据此计算函数调用关系的相似性以及函数对应点之间的匹配边的权值；然后利用图论中的二分图最大权匹配方法计算两个恶意代码函数调用图的相似性距离。此方法提高了恶意代码相似性分析的准确性，为恶意代码的同源及演化特性分析研究与恶意代码的检测和防范提供了有力支持。

[1] Kolter J Z, Maloof M A. Learning to detect and classify malicious executables in the wild[J]. The Journal of Machine Learning Research, 2006,7:2721-2744.

[2] Hu Xin, Chiueh T, Shin K G. Large-scale malware indexing using function-call graphs[C]∥Proc of the 16th ACM on Computer and Communication Security, 2009:611-620.

[3] Gao Sui-xiang. Graph theory and network flow theory [M]. China Higher Education Press, 2009.(in Chinese)

[4] Kuhn H W. The hungarian method for the assignment problem[J]∥Naval Research Logistics Quarterly, 1955,2(1-2):83-97.

[5] Krane D E, Raymer M L. Fundamental concepts of bioinformatics[M]. Sun Xiao, Translation. Tsinghua:Qinghua University Press, 2004.(in Chinese)

[6] Riesen K, Neuhaus M, Bunke H. Bipartite graph matching for computing the edit distance of graphs[C]∥Proc of the 6th International Conference on Graph-Based Representations in Pattern Recognition IAPRTC-15, 2007:1-12.

附中文参考文献：

[3] 高随祥. 图论与网络流理论[M]. 高等教育出版社, 2009.

[5] Krane D E, Raymer M L. 生物信息学概论[M]. 孙啸，译.北京：清华大学出版社,2004.

LIU Xing,born in 1986,MS candidate,his research interests include network and information security.

唐勇(1979-),男,湖南衡阳人，博士，助理研究员，研究方向为网络与信息安全,数据挖掘与机器学习。E-mail:ytang@nudt.edu.cn

TANG Yong,born in 1979,PhD,assistant researcher,his research interests include network and information security，and data mining and machine learning.

Similarity analysis of malware’s function-call graphs

LIU Xing,TANG Yong
(College of Computer,National University of Defense Technology,Changsha 410073,China)

The similarity analysis of malware is an important part of the current automatic analysis of malware. The paper proposes a new method of similarity analysis of malware based on function-call graphs. This method uses the similarity distance of malware’s function-call graphs (called SDMFG) to measure the similarity of two malwares’ function-call graphs, and then analyzes the similarity of the two malwares. This method improves the accuracy of similarity analysis of malware, providing a strong support for analysis of the homology and evolution characteristics of malware and malware detection and prevention.

malware;function-call graph;SDMFG;instruction sequence;max-weight matching

2012-12-03;

2013-02-17

国家自然科学基金资助项目(61003303)

1007-130X(2014)03-0481-06

TP309

10.3969/j.issn.1007-130X.2014.03.018