Matlab软件在矩阵运算教学中的应用

杨淑菊 YANG Shu-ju；宋爱苹 SONG Ai-ping

（云南经济管理职业学院，昆明650304）

线性代数是现代数学的重要分支，是解决线性问题的重要工具，它的理论和方法广泛应用于物理、化学、工程技术、计算机等各个学科领域中，是理工科学生的一门公共必修课，目前一般的线性代数教材以理论为主导思想，偏重理论体系的完整性，过多强调证明和推理，再加上该课程本身所固有的抽象性和逻辑性，计算的繁琐性，使得学生学起来费时费力，造成学之后无法应用的尴尬局面。矩阵是线性代数中一个重要的内容，学生学习矩阵的目的是学会利用矩阵这个工具区解决实际中的问题，而实际中的问题涉及到的矩阵规模比较大，笔算非常冗繁，直接影响到了问题的求解。Matlab软件是由美国Mathworks公司于1984推出的科技应用软件，具有强大的数值计算和符号计算，计算结果和编程可视化等优点。线性代数中几乎所有的运算都可用Matlab简单编程实现，教学中采取用低阶矩阵的演算讲授有关的理论，对高阶矩阵用Matlab软件处理的教学方法。这样做可提高学生应用计算机和数学知识解决实际问题的能力。下面以矩阵的乘方、特征值和特征向量为例，说明Matlab软件应用过程。

例：某地区对城乡人口流动做年度调查，发现有一个稳定的往城镇流动的趋势：①每年农村居民的2.5%移居城镇。②每年城镇居民的1%移居农村。

假定城乡的总人口数保持不变，现在总人口的60%住在城镇，并且人口流动的这一种趋势保持不变，那么一年以后住在城镇的人口所占比例为多少？20年后的比例是多少？多年后的比例为多少？

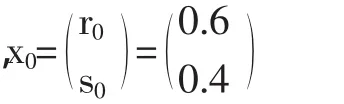
则一年之后，城镇与农村的分布为：

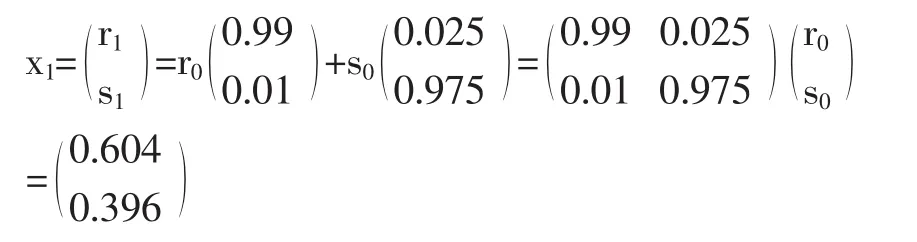
clear;A=[0.99 0.025;0.01 0.975];X=[0.6;0.4];for i=1:20;X=A*X;end;X20

运行结果为：x20=（0.66，0.34）′，该结果表明 20 年后，总人口的65.82%住在城镇，总人口的34.18%住在农村。考虑多年后城乡人口平衡时的比例，只需在Matlab的命令窗口再输入：X=[0.6;0.4];C=[1 1]';n=0;while X～=C;C=X;n=n+1;X=A*X;end;format rat;X,n

用Matlanb的eig(A)命令可求矩阵A的特征值和特征向量，只需在Matlab中输入：clear;A=[0.99 0.025;0.01 0.975];[P,T]=eig(A),format rat;

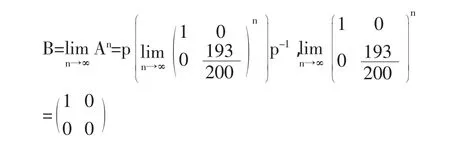
根据上面的分析，只需在Matlab命令窗口输入：

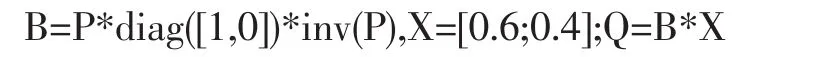
上述问题是简单人口的迁移模型，该模型还可用于研究我国当前农村的城镇化和与城市化过程中农村人口与城市人口的迁移问题。这个模型还可广泛应用于生态学、经济学和工程学的许多领域。教学中让学生用同样的方法去解决生态学、经济学、工程学中的相应问题，能提高学生数学建模能力。

从上面实例可以看出，线性代数中很多冗繁的笔算计算问题在Matlb中只需要一条简单的命令就可以解决。可见Matlab是求解线性代数问题的强大工具，将其融入线性代数教学中不仅能激发学生的兴趣，又能培养学生解决问题的能力，为学生后续课程中应用线性代数知识打下了良好的基础，也为线性代数教学适应信息化社会提供了良好的借鉴作用。

[1]吴赣昌，线性代数[M].中国人民大学出版社，2010.

[2]朱旭，李换琴，籍万新.MATLAB软件与基础数学实验[M].西安交通大学出版社，2008.

[3]林晶.Matlab在线性代数教学中的实现[J].数学学习与研究，2011(03).