近距平行跑道基于相关平行进近模式排序研究

孙 佳，田 勇

(南京航空航天大学 民航学院，南京 210016)

随着民航运输业的不断发展，航班流量不断增加，航班延误现象越来越严重，势必给航空公司带来巨大的经济损失.近距平行跑道(Closely Spaced Parallel Runway,CSPR)相比于单跑道在容量上有大幅增加，且占地面积少、投资成本低，因此，越来越成为各大、中型机场主选的平行跑道类型之一.美国联邦航空局于2011年提出了近距平行跑道相关平行进近这一概念[1]，相比于现有的一起一降模式，相关平行进近模式能最大程度地提升跑道容量空间，改善近距平行跑道运行模式单一的现状.

影响跑道容量的决定性因素是连续航班流之间的间隔，它与天气、导航设施、航班类型等因素密切相关.因此，优化航班的着陆顺序，缩减航班流之间的间隔，对提高机场容量，增大机场流量意义重大[2].国内外学者对进场航班排序已有一定的研究，主要是通过建立混合整数线性规划模型，应用遗传算法[3]、蚁群算法[4]、模糊办法[5]等方法进行求解，但对于近距平行跑道的航班排序研究则较少，特别是对于新近提出的相关平行进近模式，更是处于研究空白状态.本文建立相关平行进近模式的近距平行跑道航班排序模型，综合考虑各个约束条件，计算在该模式下的航班延误成本，并与一起一降模式的延误成本进行对比，凸显相关平行进近模式的优势，为未来我国实施相关平行进近提供理论基础.

1 近距平行跑道相关平行进近模式

最早提出配对进近这一思想的是美国学者Jonathan Hammer，当两架航空器建立了各自的航向道后，前机与后机可以在保持一定斜距的条件下配对进近[1-6].近距平行跑道相关平行仪表进近模式是采用配对进近的思想，对平行跑道上进近的两架航空器配备一定的雷达间隔(斜向间隔、垂直间隔).相关进近中前后机要有一定的纵向间隔.考虑到前机可能会发生错误进近，闯入后机的航向道，造成危险接近甚至碰撞的风险[7]，因此要保证后机距离前机在最小配对界限(LPB)之后，前机发生错误进近时，后机可以及时进行避让机动；考虑到若前机为重型或中型机，其产生的尾流在最大不利侧风的影响下会对后机的正常进近造成影响，为了避开尾流，要保证后机距离前机在最大配对界限(UPB)之前.相关平行进近过程中，后机的安全区域如图1所示.

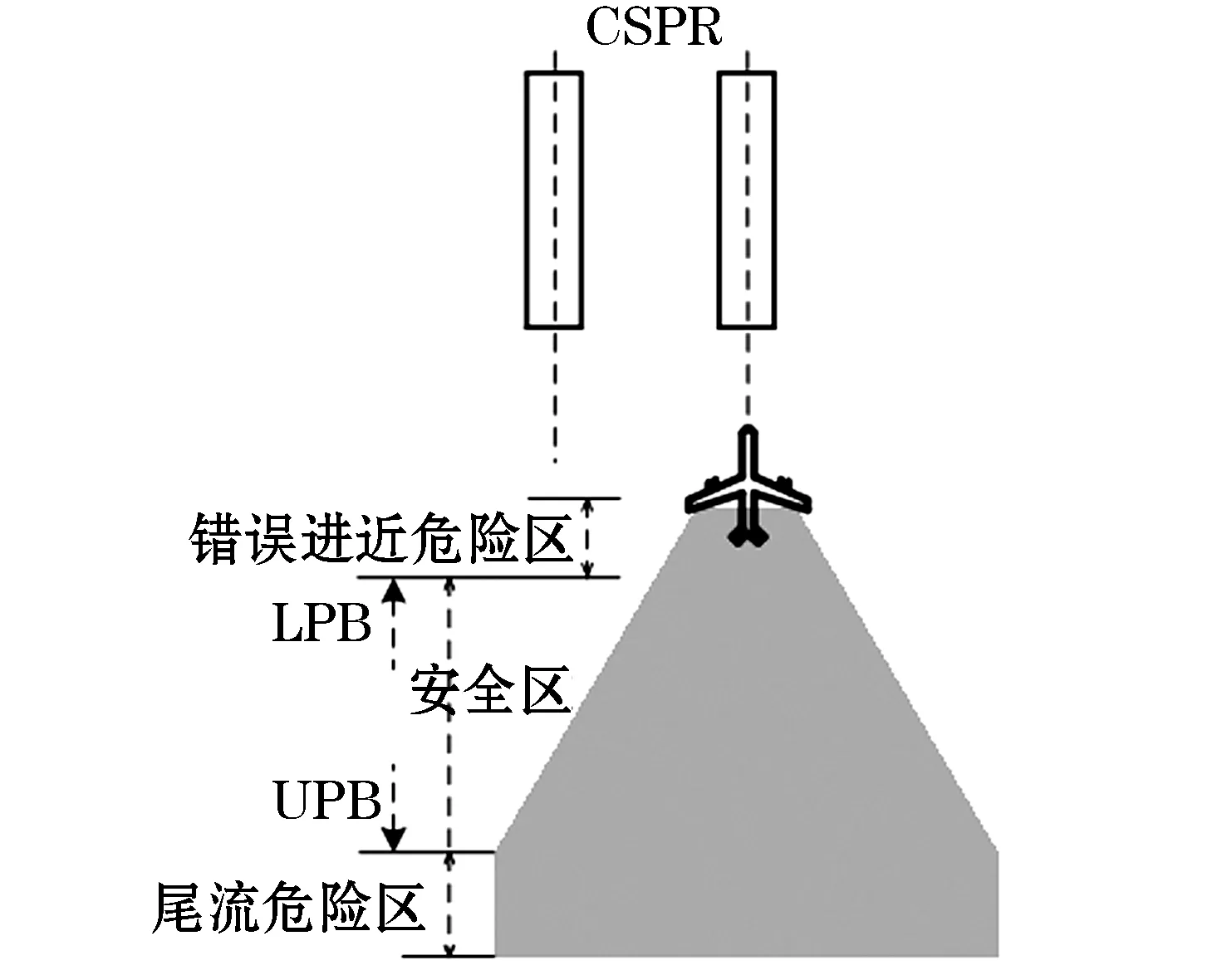
图1 相关平行进近模式下的CSPR安全区

2011年，美国联邦航空局公布了基于仪表着陆系统/微波着陆系统(ILS/MLS)的近距平行跑道相关进近程序文件，这表明美国已正式开始授权一些机场进行CSPR相关平行进近，文件规定被授权机场导航设施应满足CATI类ILS精密进近程序，需在CATI类天气条件下实施，前后机之间保证一定的斜向间隔，应用错列跑道以及满足一定的机型组合下实现CSPR的相关进近.

我国虽还未实现近距平行跑道的相关平行进近，但一起一降运行模式不能充分发挥近距平行跑道的优势，利用相关平行进近模式，实现满足约束条件的航空器之间配对进近，可以大大缩短前后机的时间间隔，从而减少延误成本，因此，对近距平行跑道相关平行进近模式的航班排序方案进行研究具有很大的经济效益.

2 着陆航班排序模型的建立

航班排序问题是指为到达航班分配不同的跑道，在满足航班间最小安全间隔的基础上充分利用机场容量，减少航班延误.某航空枢纽机场在某个时间段内共N有架航空器，tETA为航空器的预计到达时刻(ETA,estimated time of arrival)，即是该架航空器的计划着陆时刻，tSTA为航空器的实际到达时刻(STA,scheduling time of arrival)，即是该架航空器经过排序后实际到达的时刻，Ci为航班i的延误成本，建立航班的最小总延误成本为目标函数，如式(1)所示.

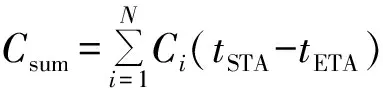
(1)

近距平行跑道的相关平行进近模式相比于现有的一起一降模式较为复杂，因此，需考虑的约束条件较多，本文主要从跑道约束、着陆时刻约束、配对约束、排序约束和间隔约束等多个约束条件着重进行分析.

2.1 跑道约束

从各个方向进场的航班流分单独着陆和配对着陆两种情况考虑跑道分配约束.单独着陆的航空器遵循规则R1，配对着陆的航空器遵循规则R2，如式(2)、(3)所示.

R1={(m,y)|m∈M,y∈Y}

(2)

R2={((m1,y1),(m2,y2))|m1,m2∈Mandy1,y2∈Y}

(3)

式(2)表示单独着陆的航空器从m方向进场航班着陆在跑道y上，式(3)表示配对着陆的航空器前机m1着陆在跑道y1上，后机着陆在跑道y2上.

以某机场终端区为例，有五个方向的着陆航班流，分别为m1,m2,m3,m4,m5，如图2所示，建立其跑道分配规则R为：

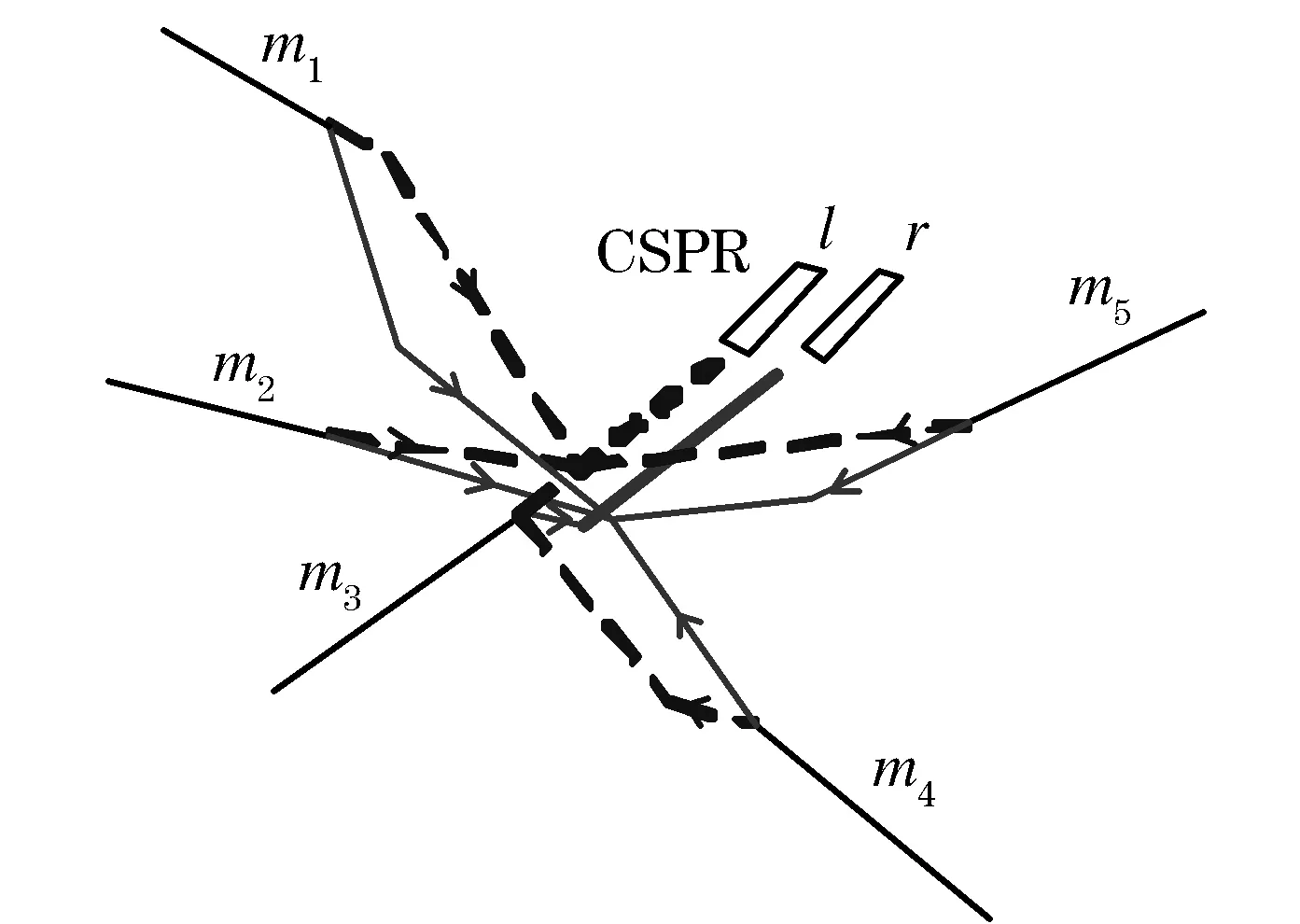
图2 某机场终端区着陆航班流示意图

R=R1∪R2

(4)

R1={(m1,l),(m2,l),(m3,l),(m4,r),(m5,r)}

(5)

R2={((m1l,l),(m1,r)),((m1,l),(m2,r)),((m1,l),(m3,r)),((m1,l),(m4,r)),((m1,l),(m5,r)),

((m2,l),(m2,r)),((m2,l),(m3,r)),(m2,l),(m4,r),((m2,l),(m5,r)),

((m3,l),(m3,r)),(m3,l),(m4,r),(m3,l),((m3,l),(m5,r)),

((m4,l),(m4,r))((m4,l),(m5,r))

((m5,l),(m5,r))}

(6)

式(5)表示单独着陆的航空器的跑道着陆规则，从m1,m2,m3着陆流着陆的航空器从左跑道着陆，从m4,m5着陆流着陆的航空器从右跑道着陆；式(6)表示配对着陆的航空器的跑道着陆规则，着陆航班流靠右的航空器，在配对进近中，在右跑道上配对着陆，相反，着陆航班流编号较小的航空器，在配对进近中，在左跑道上配对着陆.

2.2 着陆时刻约束

航空器排序后的着陆时刻应当比最晚预计到达时刻(ti,L-ETA)要早，应当比最早预计到达时刻(ti,E-ETA)要晚，如式(7)所示.

ti∈[ti,E-ETA,ti,L-ETA],∀i∈(1,…,N)

(7)

2.3 配对约束

定义两个决策变量zij和yij，其中，当航空器i和航空器j配对进近且航空器i为配对前机时，zij=1，否则，zij=0；当航空器i和航空器j非配对进近且航空器i在航空器j之前时，yij=1，否则，yij=0.航空器在相关平行进近过程中应遵循配对约束，如式(8)～(10)所示.

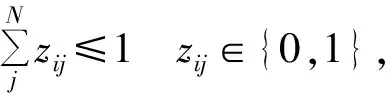
(8)

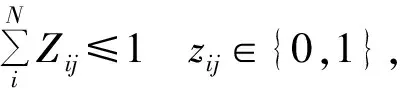
(9)

对于i,j∈(1,…,N),i≠j:

zij+zij+yij+yit=1,zij,zji,yij,yij∈{0,1}

(10)

式(8)表示第架航空器仅可以与一架航空器配对进近且作为配对航空器的前机.式(9)表示第j架航空器仅可以与一架航空器配对进近且作为配对航空器的后机.式(10)表示航空器i和航空器j配对且前机为航空器i，或前机为航空器j；航空器和航空器j不配对且前机为航空器i，或前机为航空器j.

2.4 排序约束

在同一着陆航班流中，航空器着陆顺序不能改变，即排在较后的航空器不能比排在较前的航空器先着陆.对于在着陆航班流mk(k∈{1,…,5})中的任意航空器i和航空器j，若ti,ETA≤tj,ETA,则需满足ti,STA≤tj,STA.

2.5 间隔约束

对于单架航空器或配对的航空器之间均应保持一定的纵向时间间隔.对于不能配对的航空器之间应根据民航局86号令《中国民用航空空中交通管理规划》(CCAR-93TM-R2)第46条：“前后起飞离场或前后进近着陆的航空器，其雷达间隔的尾流间隔最低运行标准如下规定”，在本文中见表2所示.

表2单跑道运行下不同机型组合时的最小尾流间隔

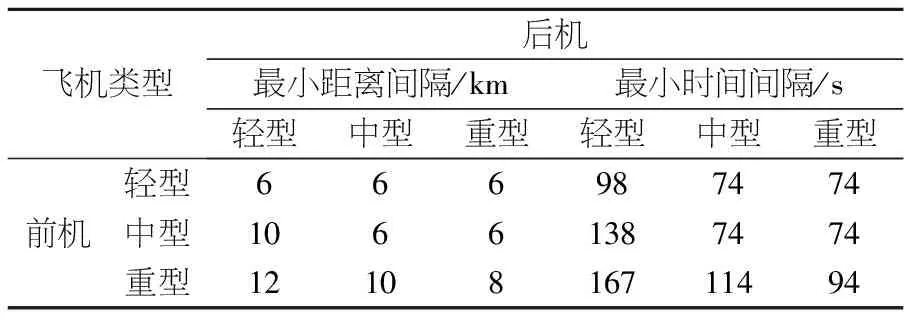
飞机类型后机最小距离间隔/km最小时间间隔/s轻型中型重型轻型中型重型轻型666987474前机中型10661387474重型1210816711494

对于配对的航空器对，本文考虑最小配对界限时间tLPB=5 s，最大配对界限时间tUPB=25 s，综合考虑各种情况，可以得到如式(11)～(13)所示的配对间隔时间约束.

对于i,j∈(1,…,N),i≠j:

ti-ti≥-(yji+zji)·C+yij·Δtij,yjizjt,yij∈{0,1}

(11)

tj-ti≥-(yji+zji)·C+(yij+zij)·tLPB,zjt,yjt∈{0,1}

(12)

tj-ti≤(yij+zji)·C+zij·tUPB,zjt,yij∈{0,1}

(13)

其中：ti、tj分别表示航空器i,j的排序后着陆时刻；C为一较大常数，本文中取C=105min；Δtij表示航空器i,j需保持的最小间隔时间要求，当航空器i,j未配对时，该最小间隔要求参考表2；当航空器i,j配对时，本文考虑该最小间隔要求为15 s.

相关平行进近模式的近距平行跑道航空器进近过程中，根据前后机的机型、前机着陆的跑道以及安全区域等条件的限制，前后机并非都能配对成功，本文考虑四架连续着陆航班，即航空器、航空器、航空器和航空器，则四架航空器可能出现的配对情况如下四种情况：

1)航空器i和航空器j配对，航空器k和航空器l未配对；

2)航空器i和航空器j配对，航空器k和航空器l也配对；

3)航空器i、航空器j、航空器k和航空器l均未配对；

4)航空器i和航空器j未配对，航空器k和航空器l配对.

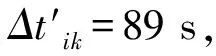
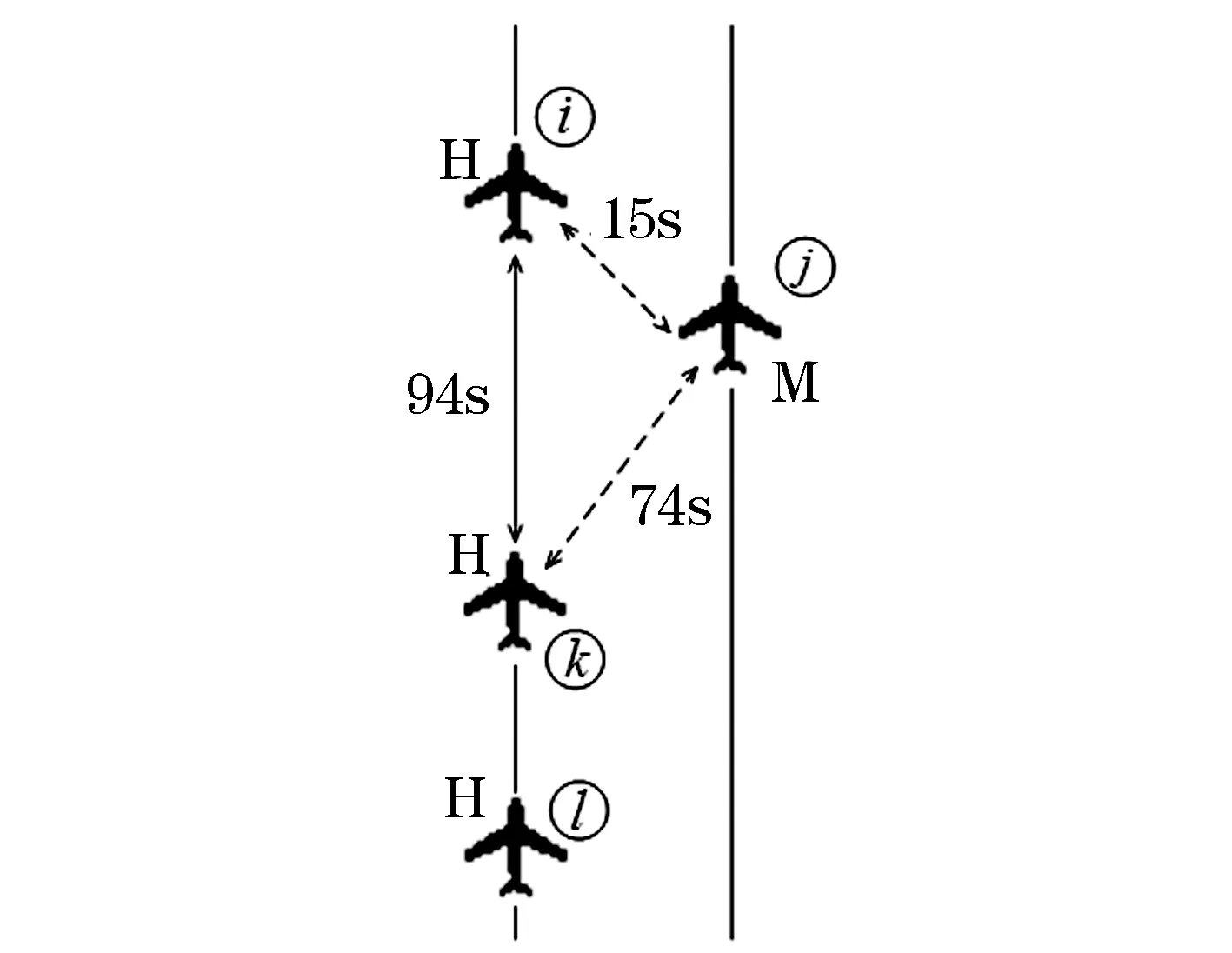
图3 第1种情况下间隔约束示例图

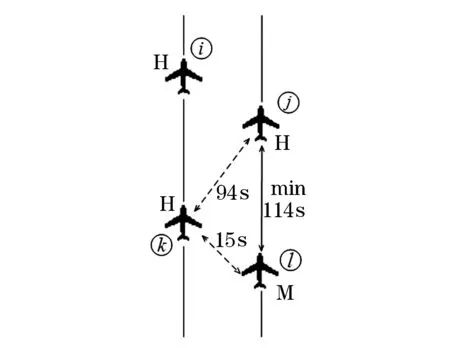
图4 第2种情况下间隔约束示例图

3 模型求解算法及仿真程序设计

由于对相关平行进近模式的近距平行跑道排序方案研究还处于起步阶段，因此本文采用改进的先到先服务(FCFS)算法，综合考虑跑道约束、着陆时刻约束、配对约束、排序约束和间隔约束等约束条件，对模型进行求解，具体步骤如下：

步骤1：初始化N架航空器航班计划时刻，建立航班着陆流队列，每一队列按照tETA进行排序.

步骤2：从每一个着陆航班流队列中选出第一架航空器并按tETA进行排序，组成队列C，继续下一步.

步骤3：按照跑道约束条件分配航空器着陆跑道，判断前后机是否满足配对约束条件，若是，则按配对时间间隔进近，ti,STA=max{ti,ETA,(ti-1,STA+15),(ti-2,STA+Δti-2,i)},并将C其从队列剔除；若否，则按航空器尾流间隔进近，ti,STA=max{ti,ETA,(ti-1,STA+Δti-1,i),(ti-2,STA+Δti-2,1)}，并将其从队列中剔除；继续下一步.

步骤4：转步骤2，重新排序，直到C为空，继续下一步.

步骤5：计算总的延误成本，算法结束.

根据设计的算法，采用Visual C++进行编程，图5为相关平行进近模式的仿真算例流程图.

4 实例分析

上海虹桥国际机场作为我国长三角地区的交通枢纽机场，飞行流量大且趋于饱和，现阶段的近距平行跑道(18L/36R、18R/36L)一起一降运行模式虽较单跑道的容量有一定的提高，但并未最大程度地发挥近距平行跑道的优势.本文结合上海虹桥国际机场的实际情况粗略设计近距平行跑道相关平行进近各个方向的进近航线，如图6所示，分三个方向的进近航班流，在此基础上建立跑道约束，如式(14)、(15)所示.

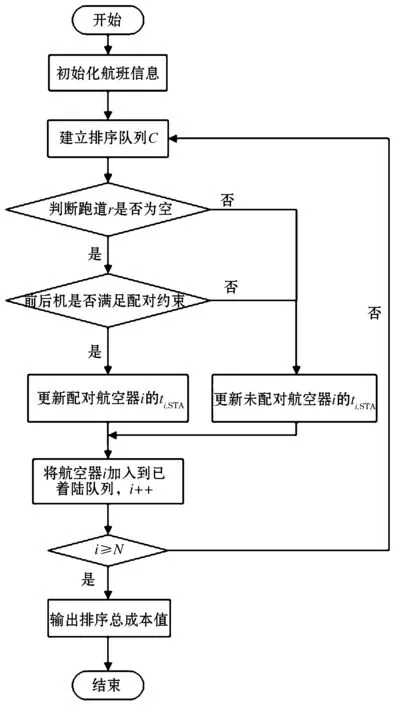
图5 仿真算例流程图

R1={(CHONGGU,36L),(DADAT,36L),(BELOP,36r)}

(14)

R1={((CHONGGU,36L),(CHONGGU,36R)),((CHONGGU,36L),(DADAT,36R)),

((CHONGGU,36L),(BELOP,36R)),((DADAT,36L),(DADAT,36R)),

((DADAT,36L),(BELOP,36R))}

(15)

式(14)表示从CHONGGU和DADAP方向进近的航空器在36L号跑道单独着陆，从BELOP方向进近的航空器在36R号跑道单独着陆；式(15)表示从CHONGGU,DADAT,BELOP进近的航班流配对进近时需着陆的跑道.

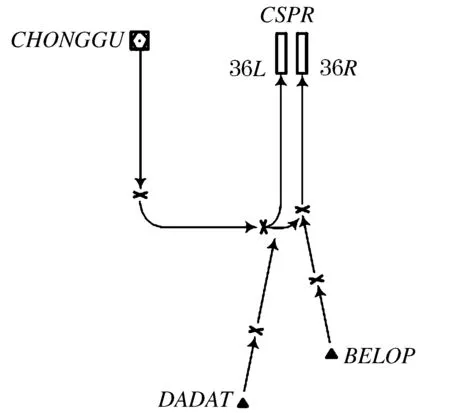
图6 上海虹桥国际机场进场航线示意图

假设各方向的着陆航班流繁忙程度均衡，采用某时间段的20架航班时刻作为原始数据，设定tLPB=5 s，tUPB=25 s，当航空器i,j配对成功时，Δtij=15 s，当航空器i,j未配对成功时，Δtij参考表2尾流间隔标准.本文考虑重型机和中型机两种机型，重型机以B747-400为例，中型机以B737-500为例，重型机和中型机的每分钟延误损失分别为360.8元、143.3元.采用Visual C++对模型进行仿真计算，可得到各航班的延误时间及总的延误成本，对比近距平行跑道采用一起一降模式时，采用FCFS计算航班排序后的延误成本.见表3.

表3航班信息和排序仿真结果

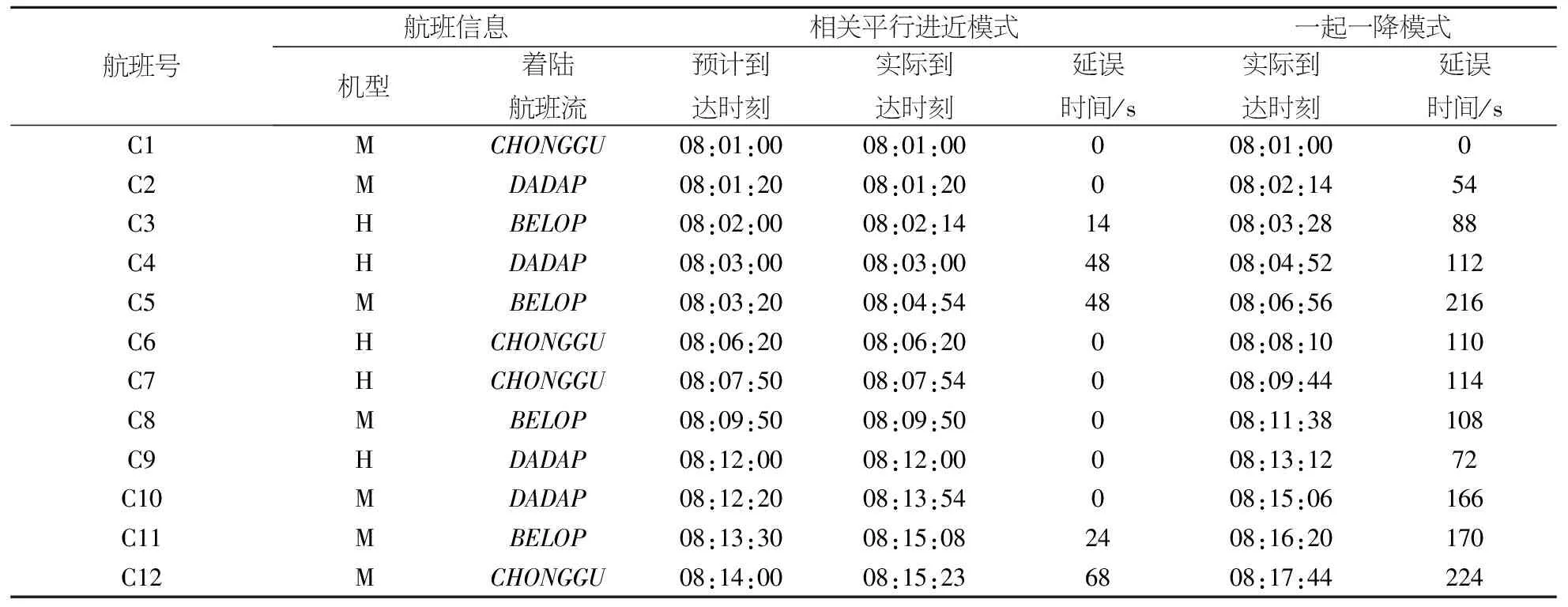
航班号航班信息相关平行进近模式一起一降模式机型着陆航班流预计到达时刻实际到达时刻延误时间/s实际到达时刻延误时间/sC1MCHONGGU08:01:0008:01:00008:01:000C2MDADAP08:01:2008:01:20008:02:1454C3HBELOP08:02:0008:02:141408:03:2888C4HDADAP08:03:0008:03:004808:04:52112C5MBELOP08:03:2008:04:544808:06:56216C6HCHONGGU08:06:2008:06:20008:08:10110C7HCHONGGU08:07:5008:07:54008:09:44114C8MBELOP08:09:5008:09:50008:11:38108C9HDADAP08:12:0008:12:00008:13:1272C10MDADAP08:12:2008:13:54008:15:06166C11MBELOP08:13:3008:15:082408:16:20170C12MCHONGGU08:14:0008:15:236808:17:44224

续表

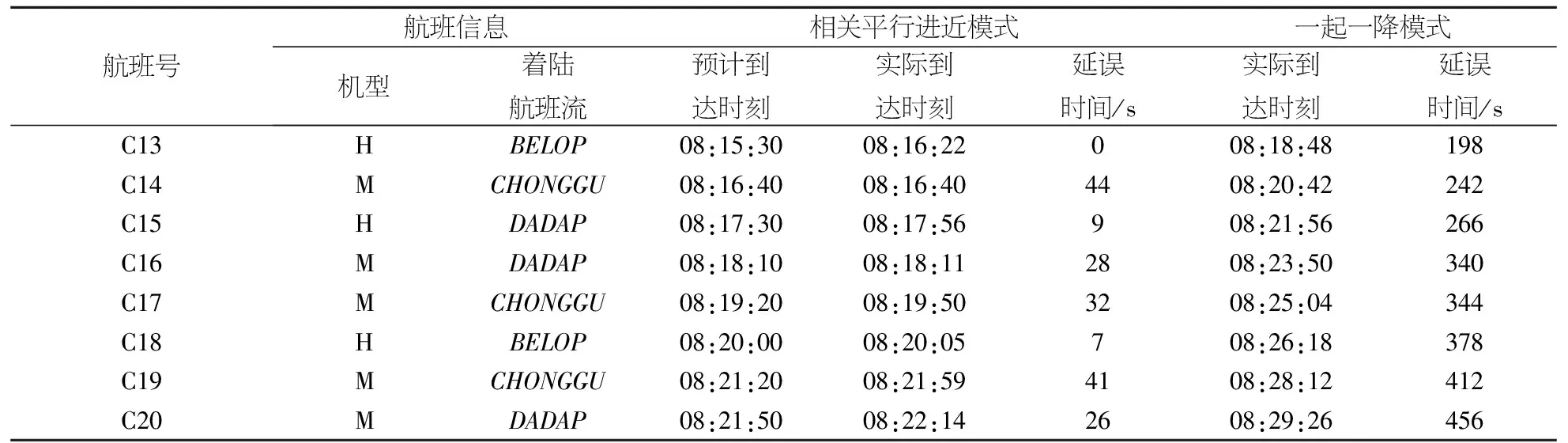
航班号航班信息相关平行进近模式一起一降模式机型着陆航班流预计到达时刻实际到达时刻延误时间/s实际到达时刻延误时间/sC13HBELOP08:15:3008:16:22008:18:48198C14MCHONGGU08:16:4008:16:404408:20:42242C15HDADAP08:17:3008:17:56908:21:56266C16MDADAP08:18:1008:18:112808:23:50340C17MCHONGGU08:19:2008:19:503208:25:04344C18HBELOP08:20:0008:20:05708:26:18378C19MCHONGGU08:21:2008:21:594108:28:12412C20MDADAP08:21:5008:22:142608:29:26456

由表3可以看出，采用改进的FCFS算法对排序模型进行求解，得到近距平行跑道相关平行进近模式下上海虹桥国际机场某时间段的航班延误情况，总延误时间为564 s，总延误成本为1 051.8元；采用传统的FCFS算法计算近距平行跑道一起一降模式下的航班延误情况，可以得到，航班总延误时间为4 070 s，总延误成本为14 570.8元.从分析结果可以看出，近距平行跑道采用相关平行进近模式能很大程度地减少航班延误，节约延误成本，为航空公司带来巨大的经济效益，因此，近距平行跑道实施相关平行进近具有重要的意义.

5 结 语

本文阐述了近距平行跑道的相关平行进近模式，建立了相关运行模式下的着陆排序模型，以总延误成本最小为目标函数，综合考虑跑道约束、着陆时刻约束、配对约束、排序约束和间隔约束等约束条件，采用改进的FCFS算法对模型进行了求解，并以上海虹桥国际机场为例，得到了某一时间段内20架航空器采用相关平行进近模式的延误时间及总延误成本，将仿真数据与一起一降模式的延误时间和总延误成本进行对比分析，凸显了相关平行进近模式的经济性.由于对近距平行跑道相关平行进近模式的研究还处于起步阶段，因此本文着重排序模型的建立，未来将在算法的改进方面进行重点研究.

参考文献：

[1] RDER JO 7110.308, 1.5-Nautical mile dependent approaches to parallel runways spaced less than 2500 feet apart[S].

[2] 丁 峰, 贺尔铭, 吴盘龙. 空中交通自动化管理中飞机等待队列的排序算法[J].西北工业大学学报, 2001, 19(3): 456-460.

[3] BEASLEY J E, SONANDER J, HAVELOCK P. Scheduling aircraft landings at London Heathrow using a population heuristic[J]. Journal of the operational Research Society, 2001, 52: 483-493.

[4] 李志荣, 张兆宁. 基于蚁群算法的航班着陆排序[J].交通运输工程与信息学报, 2006, 4(2): 66-69.

[5] JOHN E. Fuzzy reasoning-based sequencing of arrival aircraft in the terminal area[C]//AIAA Guidance, Navigation and control Conference,New Orleans, LA, 1997: 1-11.

[6] HAMMER J. Case study of paired approach procedure to closely spaced parallel runways [J]. Air Traffic Control Quarterly, 2000, 8(3): 223-252.

[7] 孙 佳，田 勇.近距离平行跑道配对进近中的碰撞风险分析[J]. 哈尔滨商业大学学报：自然科学版，2014，30(2)：241-245.