加权Markov链权重计算及其应用
2014-09-14周庆欣吴玉东范红霞孙李红王树忠
周庆欣,吴玉东,范红霞,王 旭,孙李红,王树忠
(哈尔滨商业大学 基础科学学院, 哈尔滨 150028)
股票市场是一个国家的晴雨表,它充分反映着一个国家的经济运行状况.股票价格的联动效益在世界各市场中日益表现出来,也反映出了市场的资本价格.股票价格随时间的变化一直对预测者有巨大的吸引力,也是各种预测方法应用的热门领域.
Markov是享誉世界的著名数学家,在1906~1912年期间,他提出并研究了一种能用数学分析方法研究自然过程的一般图式,后人把这种图式以他的姓氏命名为Markov链.Markov链是一种特殊的随机过程,它具有Markov性,即未来状态不受过去状态影响.Markov性所表达的是在已知“现在”的条件下,“将来”与“过去”是独立的,这种性质也称“无后效性”[1].
加权Markov链在Markov链基础上在权重方面进行了改进.国内各行业的科技工作者都在运用加权马氏链理论结合实际情况进行预测.从预测的方法上来看,有直接用加权Markov链转移概率来做预测的;有结合模糊数学利用Markov链来预测的;有结合时间序列线性模型利用Markov链来预测的;还有各种利用加权Markov链来预测的[2-4].从预测的结果看,加权Markov链的实用性和准确性较高,思路清晰.客观易懂、计算简便、准确可靠值得我们进行研究和推广.
1 加权Markov链基本理论
1.1 随机过程的“马氏性”检验
检验随机变量序列是否具有“马氏性”,是应用加权Markov链模型分析和解决实际问题的必要前提.对于离散序列的加权Markov链,一般用χ2统计量来检验.具体方法如下:

1.2 加权Markov链进行预测的基本步骤
股票收盘价是随时间的变化而变化的随机序列,所以我们可以对股票的收盘价进行分析,并预测下一状态股票收盘价的变化区间.现以股票市场股票价格变化Xn(元)为随机序列,搜集按时间序列排序的股票收盘价构成随机序列Xn,根据加权马尔可夫预测的基本思想,按如下步骤进行[6]:
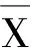
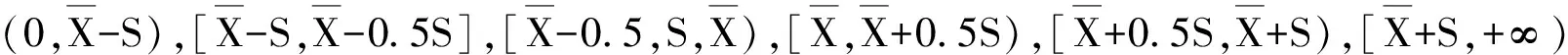
3)依据第二步的分级标准,分别确定不同时间段的股票价格的状态值.
4)对已知序列指标值进行“马氏性”检验.通常χ2用统计量来检验:当统计量
服从自由度为(m-1)2的χ2分布时,该序列具有马氏性.其中fij为从状态i到状态j的频数,m为序列状态数,pij为从状态i到状态j的一步转移概率,pkj为j状态的边际概率.
5)计算序列指标值的各阶自相关系数rk以及各种步长的马尔可夫链权重wk.
(1)
(2)
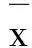
6)根据第三步所确定的序列状态值,统计步长分别1,2,…,6的转移概率矩阵.
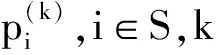
8)根据不同步长将同一状态的各预测概率加权和作为指标值处于该状态的预测概率,则该时刻指标值所对应的预测状态j应满足:pj=max{pi,i∈E}.
将同一状态的各预测概率加权和作为指标值处于该状态的预测概率,即

9)对该马尔可夫链其他特征进行分析.
2 加权Markov链预测的实证分析
2.1 实例中的“马氏性”检验
针对中体股价为研究对象,若要使用加权Markov链对股票收盘价进行预测,必须首先对其“马氏性”进行检验.现以中体产业2009年2月6日~2010年6月11日70个交易周的股价变动情况为例,运用加权Markov链模型进行预测.
通过大智慧行情软件采集到的中体产业在2009年2月6日~2010年6月11日的70个周的股票周收盘价,我们利用Excel软件对采集的数据进行分析.
现在以样本均方差为标准,将中体产业股票的收盘价的变动分为大跌、平跌、平下、平上、上涨和大涨等6个状态区间,对应的状态空间E={1,2,3,4,5,6}.
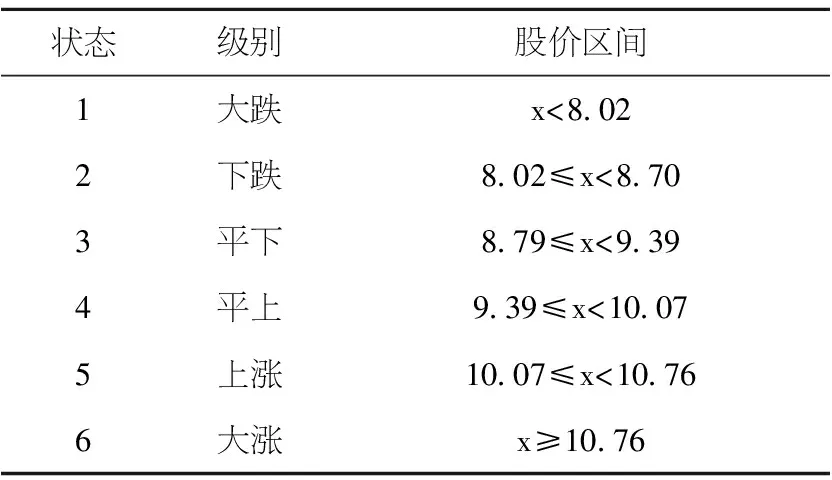
表1 中体产业股票收盘价状态划分表
由股票收盘价划分表及股价历史数据可将可以得出股票六大区域划分图,见图1.
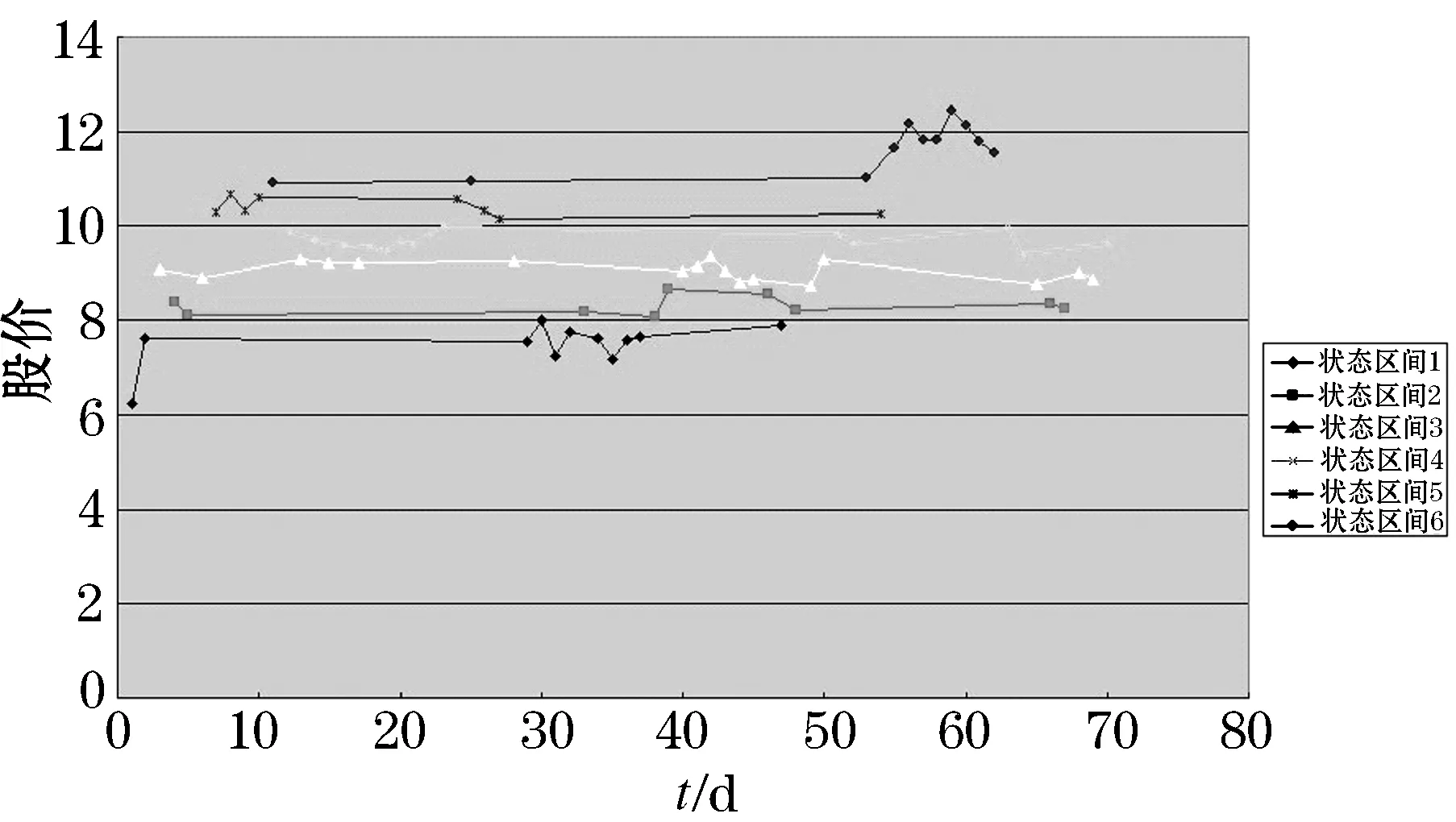
图1 中体股票收盘价依六类区间划分图
图1中,横轴代表时间,纵轴代表股价,系列i即为状态i,i=1,2,……6.图1更清晰的反映出了股票收盘价的划分区域.各步长的转移概率矩阵为:
(3)
由式(3)可计算得各步长的转移概率矩阵pij(k) ,式中fij(k)表示从状态经过步转移到状态的频数.
为了利用加权Markov链对股价进行预测,现对过程进行“马氏性”检验.针对2009年2月6日~2010年6月11日期间的70个周的收盘价数据进行统计,得出股价各状态间的频数矩阵fij如下:
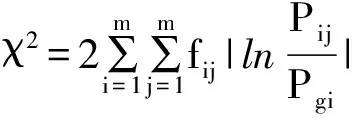
2.2 权重的计算
加权Markov链预测方法和Markov链预测方法的主要区别就在于初始状态的权重.加权Markov链预测得初始状态的权重不简单的只为1或0,而是根据合理的计算公式对每一状态进行分析,重新计算权重.现在将权重的计算方法示例介绍如下[7-8].
根据前面介绍的加权马尔可夫链模型在股价预测中的预测方法,由公式,计算各阶自相关系数和各步长的权重,见表2.

表2 各阶自相关系数和各步长的权重
表2中的各阶自相关系数和各步长的权重都是式(1)、(2)计算出来的,以方便下面对价格区间的预测.其中k表示自相关阶数,rk表示各阶自相关系数,wk表示各步长的马尔可夫链的权重,从而可以为后面求取各状态的预测概率做好准备.
2.3 价格区间的预测
我们对未来股价所处的状态进行预测,如果依据第66,67,68,69,70周的股票收盘价为初始状态及其相应的状态转移概率矩阵对第71周股票的收盘价进行预测,由公式
可得表3.
由表3知,max{pi,i∈E}=0.4414,此时i=3,即第71周中体产业股票的收盘价状态为3(即为平下),收盘价满足区间8.70≤x<9.39,概率为44.14%.由历史记录的资料知,第71周的实际收盘价为8.70,与预测区间相符.
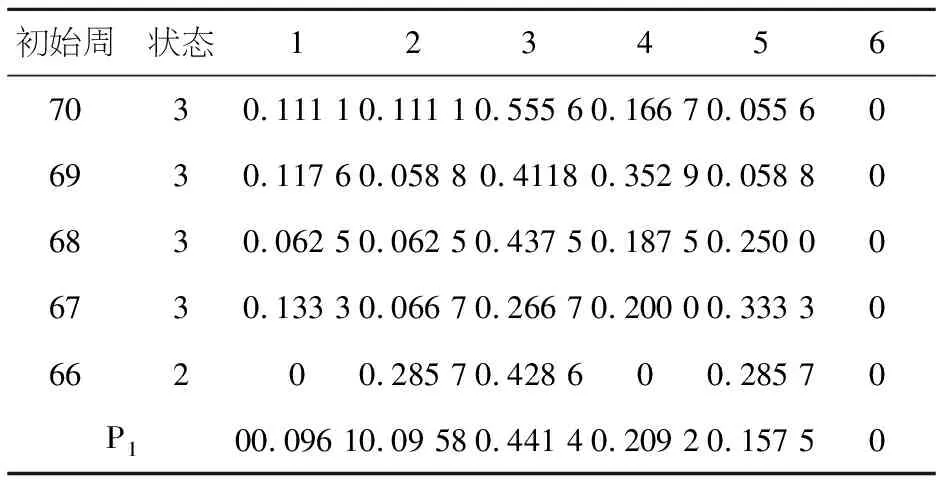
表3 第71周股票收盘价状态预测表
接下来将第71周的状态加入初始状态,也就是以67,68,69,70,71周的状态作为初始状态对第72周的股票收盘价状态进行预测.利用上面的方法可以依次预测出第72,73,74,周的股票收盘价,分别为满足8.70≤x<9.39,第75,76周的股票收盘价,分别为满足9.39≤x<10.07.而实际收盘价分别8.9,9.20,9.38,9.43,9.63,预测结果与实际结果相符.
3 模型的评价
另一方面,我们利用Markov链预测方法对未来几周的股票收盘价进行预测,预测结果表明,加权Markov链的预测结果更接近实际值,而Markov链预测的误差相对较大.下面用这两种预测方法对股票收盘价的预测误差进行比较(股价实际值为8.70).见表4.

表4 第71周预测中两种预测方法结果的比较
在Markov链进行预测的工程中,一般假定外部经济条件比较稳定,也就是所要预测的区间不会出现利好或者利空的消息使股票价格暴涨和暴跌.但是在实际股价市场中,这完全是可能的,所以这两种方法较适用于短期的预测,对于中长期的预测结果不是很理想.
本文在应用模型时只是选取了70个数据,对于更高精确度上的预测来说还远远不够.另外,如何更好的划分各状态区间以提高预测精度,也值得进一步的深入研究.
4 结 语
本文基于股票价格和期权价格序列的马氏性,用加权马尔科夫模型预测股票价格变化区间、运行周期和期权价格的变化,为个人或集体进行个人投资提供一定的参考价值. 由于股票和期权投资风险较大,影响投资回收期的因素也比较复杂,在积累了足够多的股票价格、期权价格数据后可以对股票价格、股票回收期以及期权价格的变化进一步丰富和完善,发现分析结果与实际数据一致.而且资料的代表性日益增强,自相关系数、状态转移矩阵、权重将会发生一定的变化,而这种变化将使得预测更加完善,进一步提高预测的精度.
参考文献:
[1] 王 军,王 娟.随机过程及其在金融领域中的应用[M]. 北京:清华大学出版社、北京交通大学出版社,2007.
[2] 纪跃芝,史 磊. 马尔可夫链及其在经济预测中的应用[J]. 长春工业大学学报:自然科学版, 2003, 24(2): 26-28.
[3] 宋庆龙,宋程成.马尔可夫链在市场经济预测中的应用[J]. 商业研究, 2009(2): 46-49.
[4] 党小超,郝占军,王筱娟. 模糊加权Markov链的用户行为预测[J]. 兰州大学学报:自然科学版, 2011, 47(1): 109-114.
[5] 樊平毅.随机过程理论与应用[M]. 北京:清华大学出版社,2005
[6] 金峻炎,陈 进.加权马氏链在房地产投资回收期预测中的应用[J]. 湖南科技大学学报, 2010, 6: 25-66.
[7] 庄悉备,伍海华.加权马尔科夫理论及在股市中的应用[J]. 金融经济, 2008(2): 82-83.
[8] 周庆欣.Markov分解法在企业经营中的应用[J].哈尔滨商业大学学报:自然科学版,2012,28(3):369-371.
