提高金属结构动态应力计算精度的方法研究

2014-09-14谭韶毅陈欢欢谢慈航

哈尔滨商业大学学报（自然科学版） 2014年6期

谭韶毅，薛璞，陈欢欢，谢慈航

(西北工业大学航空学院，西安 710072)

飞机在使用中会受到由于滑跑、突风、机动、着陆撞击以及坐舱增压等所造成的重复载荷的作用，飞机结构的一些部位特别是局部高应力区，如局部应力集中区，有缺陷区等部位就会产生由于交变应力引起的疲劳裂纹，交变应力的继续作用，使疲劳裂纹不断扩展而导致疲劳破坏.当交变载荷的频率与结构的某一阶(甚至某几阶)固有频率一致或比较接近时，结构将会发生共振，这时一定的激励将会产生更大的响应，使结构更加易于产生破坏，而且结构内部动态应力变化剧烈，常规有限元很难得到准确的动应力分布.目前对于动应力的计算思路大体基于系统运动方程对位移的求解，然后通过位移求解动应力，例如基于位移模态叠加法、直接积分法的常规有限元方法[1-5]、模态加速度方法[6]等.常规有限元法中，动应力的计算是通过单元形函数求导得到的.模态加速度方法中提出动态修正项的概念，将动态修正项应用于应力的模态叠加法中，考虑了高阶模态对动应力的影响.这几种方法对于普通动态问题，其计算精度已经可以满足正常动应力分析的需求.但是对于振动疲劳问题，由于振动应力水平是决定振动疲劳寿命的主要因素之一，微小的应力误差会导致较大的寿命预估误差[7].因此，常规的动应力计算理论无法满足我们对动态应力精度的要求，并且国内外对于提高动应力精度的研究也十分缺乏.近几年，基于模态叠加理论的虚拟激励法被越来越多的应用于结构的随机响应分析中，该方法考虑了不同模态之间的耦合效应[8].本文基于虚拟激励法以及应力的模态叠加理论，提出求解动态应力的虚拟激励法，避免了由位移求解动应力的二次误差，以及考虑了模态之间的耦合效应，从而达到提高动应力精度的要求.

1 模态叠加理论

1.1 模态叠加法

在结构动响应分析中，通常是把结构离散为线性或非线性多自由度系统，然后通过求解多自由度系统得到结构在任意激励下的动态响应.

多自由度系统的运动方程如下：

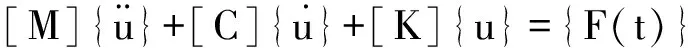
(1)

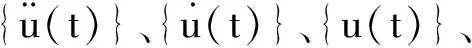
模态叠加法是基于系统运动方程，利用固有频率和振型来计算结构动响应的方法.其基本原理是：对结构自由振动进行模态分析，得到结构的固有频率和固有振型φi，利用固有振型φi组成的模态矩阵[φ]对式(1)进行解耦，将结构的动力学方程转化为各主坐标的非耦合方程.

通过坐标变换

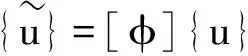
(2)

代入运动方程(1)得到：

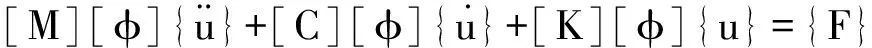
(3)

上式两边前乘[φ]T得

(4)

对式(4)进行求解，求出各主坐标的响应uj，最后利用物理坐标和主坐标的关系，得到物理坐标下的响应

(5)

其中：uj为j第模态的模态坐标；{φ}j为第j模态的模态位移向量；

在模态变换中，式(5)包含了全部的N阶模态，事实上并不需要知道所有的模态，一方面工程实际证明并不是所有的模态都能被激起；另一方面，模态位移法中，当系统中仅包含少数的一些模态时，此法将更加有效的显示出优越性.至于取几阶模态为好，一般根据精度要求或工程中的经验来定.

1.2 由模态叠加法确定动应力

根据模态叠加理论，对于线性系统，结构响应都可以表示成为模态坐标的叠加形式，所以通过模态位移法以及下面的公式，便可以确定结构的动应力

(6)

其中：uj为第模态的模态坐标，σj为第j模态的模态应力向量.

2 改进的虚拟激励法

对于平稳随机系统，离散结构受加速度激励的运动方程为：

(7)

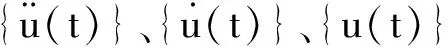
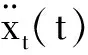
(8)

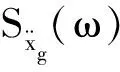
令

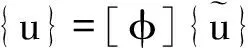
(9)

把上式代入运动方程(7)得到：

(10)

将[φ]T左乘以式(10)得到：

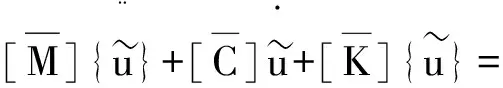
(11)

则上式可分解为个互相独立的单自由度方程

(12)

这是单自由度简谐振动方程，易得其稳态解为

(13)

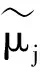
其中

(14)

ωj为模态的固有频率，ω为简谐激励的频率.

因此

(15)

根据式(6)动应力可以表示为：

(16)

因此应力的响应功率谱可以表示为：

[Sσσ]={σ}**{σ}T=

(17)

Sσσ为应力响应功率谱，γj为第j阶模态的模态参与系数，σj为第j阶模态的模态应力向量，Hj(ω)为第阶模态的频响函数.

上式即为基于应力模态叠加法的虚拟激励法，公式中计入了所有的参振振型耦合项，充分反映了模态之间的耦合效应.

3 数值计算

本文采用改进的虚拟激励法计算薄板有限元模型的动态应力，并与ABAQUS随机响应分析结果进行比较，最后通过实验数据进行验证.薄板模型尺寸为300×200 mm，厚度为1.8 mm，边界条件为四边固支，如图1所示.材料选取LY12CZ铝合金，弹性模量为E=70 GPa，密度为ρ=2 780 kg/m3,泊松比υ=0.33，直接模态阻尼比ξ=0.015.

图1 薄板模型

3.1 模态分析

通过模态分析，可以为改进的虚拟激励法提供一些所需的参量，如固有频率、模态参与系数等.采用Abaqus模态分析模块提取前10阶模态信息，如表1，2所示.

表1 固有频率

表2 模态参与系数

3.2 频率响应分析

通过Abaqus稳态瞬时模态分析，绘制危险位置处的频率响应曲线如图2所示.

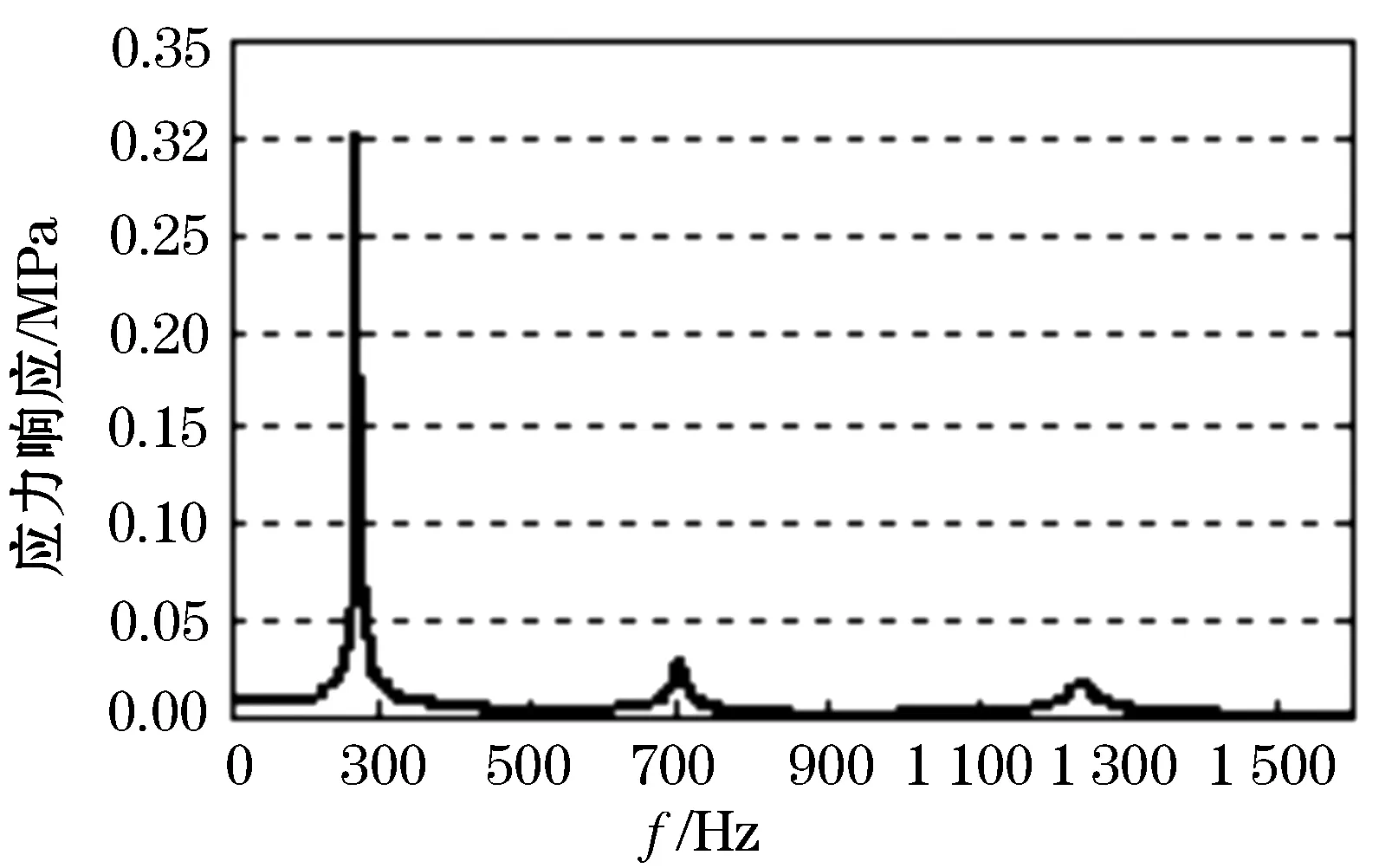
图2 危险位置处的频率响应曲线

由频率响应曲线可以看出，结构应力响应在第一阶、第四阶、第八阶固有频率附近各有一个峰值，第一阶固有频率附近的应力响应远比第四阶以及第八阶的大，通常情况下，本文只考虑第一阶模态的应力响应.但是当结构处于共振状态下，尤其是当多阶模态被同时激起时，模态之间存在耦合效应，第四阶以及第八阶模态的影响也不可忽略.

3.3 应力结果分析

本文对薄板结构施加一个频带范围为0～1 500 Hz，大小为0.2 g的高斯白噪声，使结构前10阶模态都能够达到共振状态，采用ABAQUS随机响应分析、Matlab编制改进的虚拟激励法程序对图1中1、2两节点(1、2两节点为薄板结构距离左边与顶边20mm的中心位置)的动态应力进行计算并进行比较分析，最后通过实验数据进行验证，结果如表3所示.

表3 三种方法得到的RMS应力值对比

从表3可以看出，试验得到节点1的RMS应力值为11.5 369 MPa，有限元方法得到的值为9.7 422 MPa，两者的误差为15.56%，而采用本文方法计算得到的RMS应力值为10.136 MPa，与试验结果相比，误差为12.14%，相较于有限元方法计算精度提高了21.98%左右.用同样方法所得到的节点2的计算精度提高了24.96%左右.因此可以看出，对于动态应力的计算，本文方法相较于有限元方法精度有了明显的提升，更接近试验结果.这是因为该方法避免了有限元方法中通过位移求解动应力所造成的二次误差，并且考虑了模态间的耦合效应以及高阶模态对动态应力响应的贡献.因此，该方法相较现有的有限元方法，更适用于求解结构在共振状态下的动态应力响应问题.