共固化补片预修补铝板的阻尼和疲劳寿命研究
2014-09-14李才华刘双燕
李才华,邓 琼,刘双燕
(西北工业大学 航空学院,西安 710072)
在航空航天领域,某些结构在实际应用过程中,常受到振动载荷的作用.特别是当激励频率和结构的固有频率重合或者接近时,结构会发生共振现象[1].共振引起的响应幅值远大于非共振时的响应幅值,从而导致结构迅速破坏.研究表明,共振响应的幅值主要取决于激励幅值和结构阻尼的大小[2].如果能抑制激励幅值或者提高结构的阻尼,则可以大大地降低共振引起的疲劳破坏.因此,通过提高结构阻尼比来延长结构的振动疲劳寿命成为众多学者研究的主要方法.黏弹阻尼层共固化复合材料具有高强度、高刚度和良好阻尼特性的优点,使得这种复合材料阻尼结构成为研究的热点.哈尔滨工业大学的潘利剑和张博明利用动态力学热分析技术(DMTA)测试了黏弹阻尼层共固化复合材料的动态力学性能,考察了树脂的渗透、阻尼层厚度和复合材料柔性层对共固化复合材料阻尼特性的影响[3].西安交通大学的张少辉应用基于有限元的模态应变能法研究了黏弹阻尼层共固化复合材料的损耗因子[4].青岛理工大学的张忠胜和梁森考察了共固化复合材料阻尼结构层间易脱层的问题[5].尽管有不少的研究人员对黏弹阻尼层共固化复合材料进行了研究,并应用纤维增强复合材料对结构件进行了修补[6-7],但是将黏弹阻尼层共固化复合材料应用到抑制结构振动疲劳中还鲜有研究.因此,本文针对黏弹阻尼层共固化复合材料补片,展开了如何增加结构阻尼和提高振动疲劳寿命的研究.首先,制备了黏弹阻尼层共固化复合材料补片,对四周固支薄铝板的应力集中区域进行预修补.使用基于频域的半功率带宽法测试了修补前后的结构阻尼比.其次,通过ABAQUS软件建立有限元模型,采用滞后阻尼理论计算了组合结构的等效阻尼比,并对比实验值验证了该模型.最后,用频域法估算了结构随机振动疲劳寿命,并考察了阻尼层厚度、补片长度和纤维层层数对结构等效阻尼比和振动疲劳寿命的影响.研究结果为开展结构的抗振动疲劳研究工作提供了理论支持.
1 宽带随机振动疲劳寿命估算
1.1 Dirlik 方法
宽带载荷谱的随机振动寿命的估算有很多方法,其中Dirlik方法以其估算准确而得到了广泛应用[8].Dirlik公式是通过模拟“雨流计数”的应力幅值得到应力幅值概率密度函数的半经验公式,由一个指数分布密度函数和两个瑞利分布密度函数叠加而成,计算可得到近似地接近雨流计数法的统计结果.Dirlik公式确定的应力幅值概率密度函数为[9]:
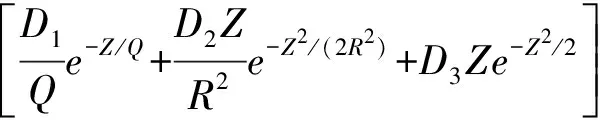
(1)
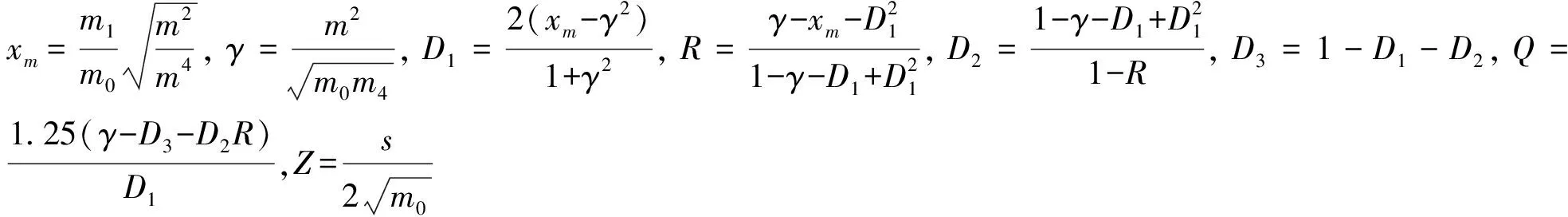
其中:m0、m1、m2、m4分别是功率谱密度函数的0、1、2、4阶惯性矩,γ为不规则因子.功率谱密度函数的n阶惯性矩公式为:
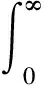
(2)
其中:G(f)为某一频率处的单边功率谱密度值.
由各阶惯性矩可以得到:
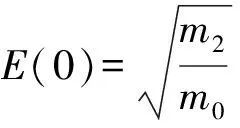
(3)
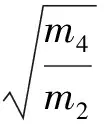
(4)
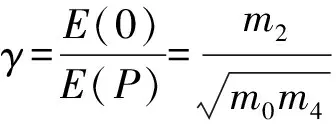
(5)
那么可以得到各个载荷的分布情况:
n(s)=P(s)E(P)T
(6)
其中:n(s)是时间长度为T,应力幅值为s的应力循环次数.
1.2 Miner线性累积损伤理论
根据Miner线性累积损伤理论,应力幅值连续变化下的累积损伤表达式:
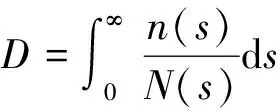
(7)
其中:n(s)为应力幅值为s的实际循环数,N(s)为破坏循环数.
材料的疲劳曲线:
SmN(s)=C
(8)
其中:m、C为材料常数,由疲劳实验获得.
令D=1,将式(6)、(8)代入式(7),可以得到结构发生破坏时的疲劳寿命表达式:
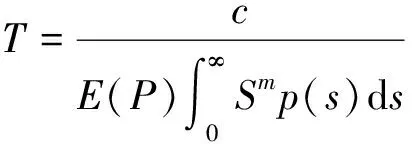
(9)
2 实验部分
2.1 实验设备和实验原理
测试结构阻尼比常用的方法有基于时域的自由衰减法和基于频域的半功率带宽法.其中半功率带宽法原理简单、操作方便,在实际测试中应用最广泛.测试原理是:实验件在固有频率点处发生共振,此时振幅达到最大,通过对这个阶段的时域信号进行FFT变换处理,可以获得实验件在共振时段内的频率响应.实验件的频率响应与阻尼系数η有密切的关系,在相同力激励的情况下,共振曲线的峰值随着η增大而降低,而这时带宽(也就是共振曲线峰值两侧下降到峰值的0.707倍)变大,表明结构振动变弱,这样可以根据振幅响应与阻尼性能的关系,通过半功率带宽法来计算结构阻尼比.由于本文考虑的主要是实验结构件第一阶固有频率对结构的影响,所以此次测试只考虑到第一阶的阻尼比.计算公式如下[10]:
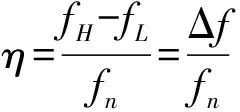
(10)
其中:fH为升高到共振频率0.707倍的频率,fL为下降时的频率,fn为第n阶共振频率,Δf为半功率带宽.
由于阻尼系数与结构阻尼比之间存在2倍的关系,结构阻尼比ζ可以由下式得到:
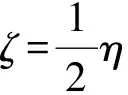
(11)
本文采用基于半功率带宽法振动台扫弦激励的方法测试四周固支的薄铝板实验件的结构阻尼比,测试系统如图1所示.

图1 补片修补下的薄铝板振动台测试系统
2.2 材料及制备工艺条件
铝板的尺寸为l=300 mm,b=300 mm,h=1.8 mm.碳纤维预浸料由威海光威复合材料有限公司生产.碳纤维复合材料补片尺寸l=120 mm,b=40 mm,h=1.12 mm.单层参数是E11=125 GPa,E22=10.3 GPa,G12=4.3 GPa,υ12=0.29,ρ=1635 kg/m3.纤维的铺设方向是与长边垂直的90°方向,共铺设八层,单层厚度0.14 mm.黏弹阻尼层共固化复合材料补片在碳纤维补片的纤维层中间嵌入0.5 mm的阻尼层,阻尼层材料为丁腈橡胶,制备时在120 ℃温度中固化3 h.共固化复合材料补片的结构如图2所示.补片胶接在薄铝板四周应力集中的区域.粘胶剂采用黑龙江省科学院石油化学研究院研制的J-302室温快速固化高强度结构粘胶剂.

图2 黏弹阻尼层共固化复合材料结构
实验件的排号规则是没有补片的薄铝板为1#件,碳纤维复合材料补片修补的薄铝板为2#件,黏弹阻尼层共固化复合材料补片修补的薄铝板为3#件.
2.3 实验条件
测试的方法是对薄铝板实验件进行定幅扫频激励,扫频的范围是实验件一阶固有频率的0.8~1.2倍.实验件的上方架设激光位移传感器,测试点位于薄铝板的中心点,记录实验件振幅的时域响应.薄铝板使用的型号是6061-T651,弹性模量72 GPa,泊松比0.33,边界条件是四周固支.
3 结果与讨论
3.1 阻尼比测试结果
四周固支薄铝板实验件结构阻尼比测试的结果如图所示.从图3~5可以看到三个实验件不同频率响应曲线,因为补片起到移频的作用,可以看到贴有补片薄铝板的一阶固有频率比未贴补片的提高了.
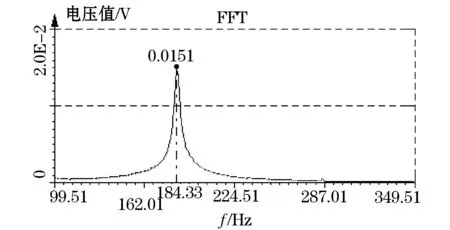
图3 未贴补片薄铝板FFT变换得到的第一阶频域响应
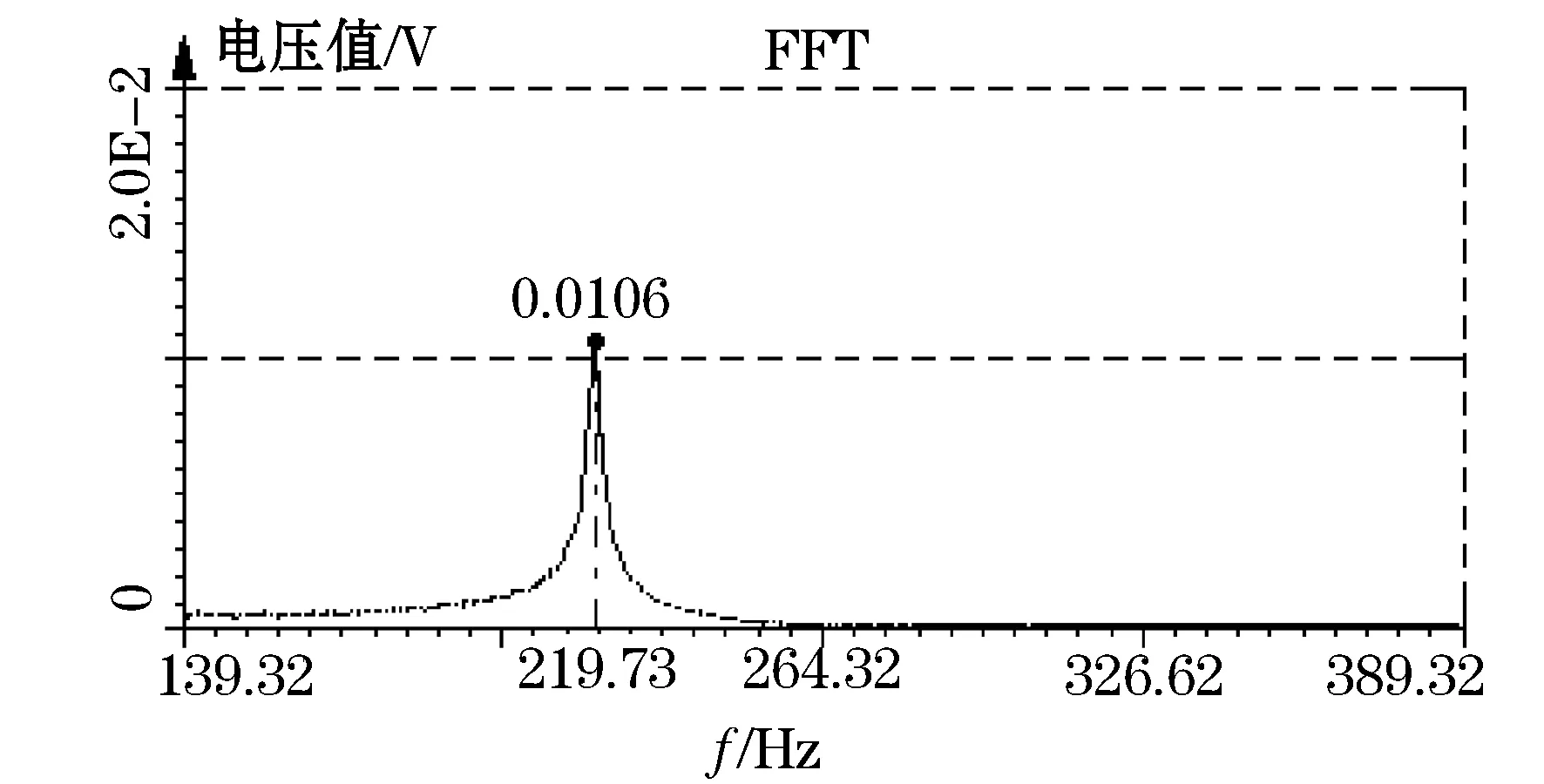
图4 碳纤维复合材料补片—薄铝板FFT变换得到的第一阶频域响应
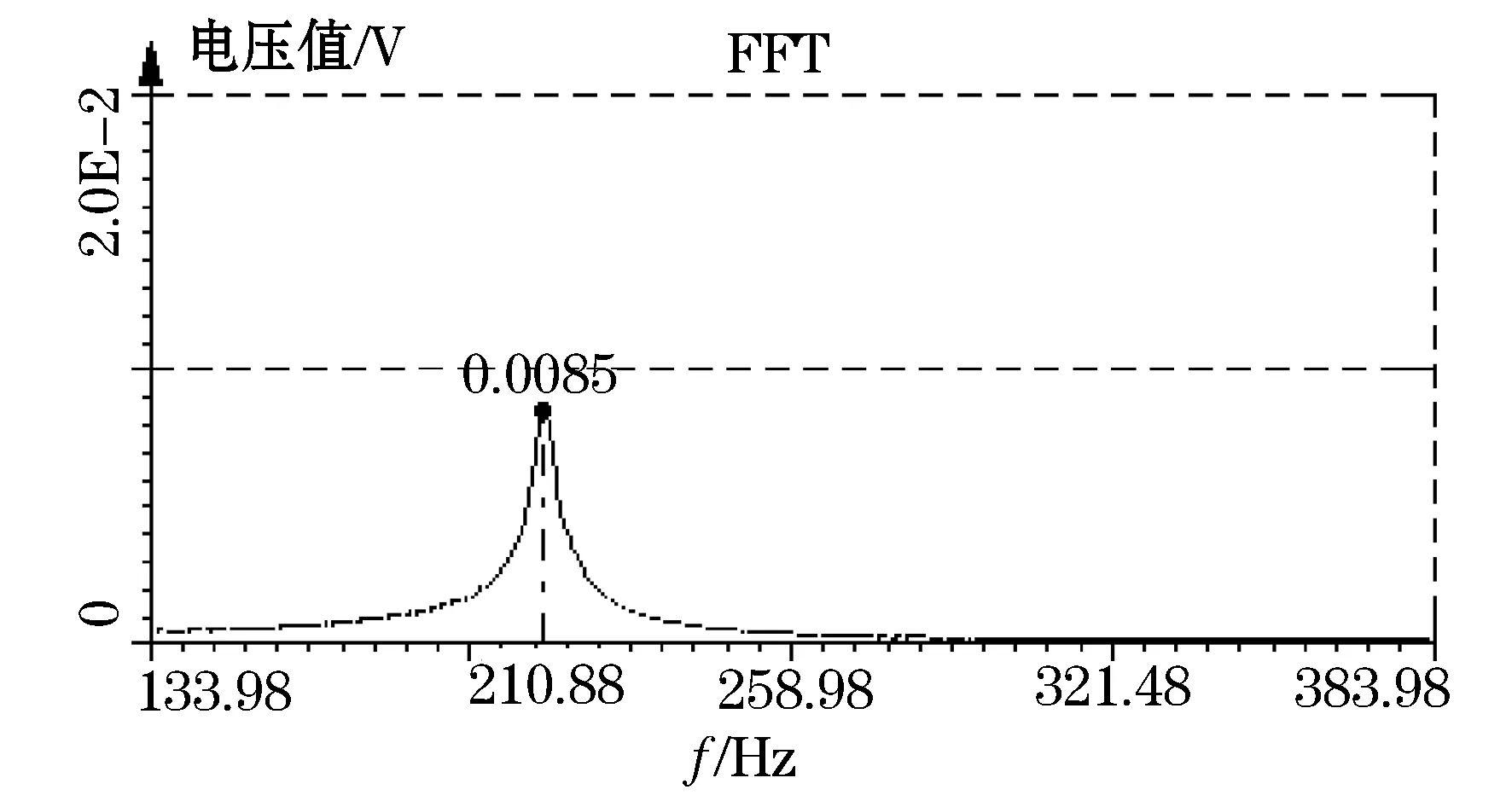
图5 共固化补片—薄铝板FFT变换得到的第一阶频域响应
时域数据经FFT转换后成频域响应后,将通过半功率带宽方法计算三个实验件的结构阻尼比,结果如表1所示.
从表1可以看出,贴有碳纤维复合材料补片的2#件、黏弹阻尼层共固化复合材料补片的3#件均比未贴补片的1#验件结构阻尼比增大,而3#件补片起到的阻尼作用更明显.显然,黏弹阻尼层共固化复合材料补片可以较大地提高实验件的结构阻尼比.
表1结构件一阶固有频率和阻尼比的实验值和仿真值对比
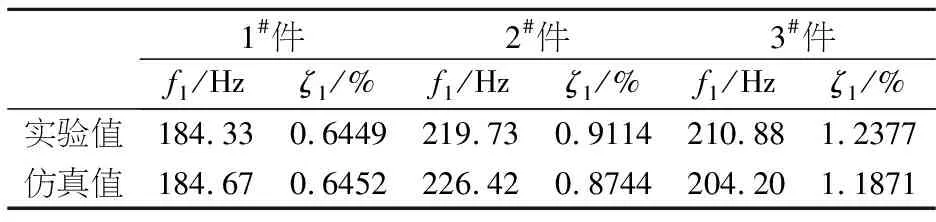
1#件2#件3#件f1/Hzζ1/%f1/Hzζ1/%f1/Hzζ1/%实验值184.330.6449219.730.9114210.881.2377仿真值184.670.6452226.420.8744204.201.1871
3.2 有限元仿真
结构阻尼比是使用有限元仿真结构振动分析的必要参数之一,以往只能是通过实验测试来得到结构阻尼比,再返回有限元模型进行振动分析.这样尽管能较为精确地设置结构阻尼比,但是并不高效,尤其在结构设计阶段需要不断调整外状,结构阻尼比也随之变化,不可能每次都经过实测来得到结构阻尼比,这样就需要寻求一个简单、方便的方法来计算结构阻尼比.这样,本文通过建立有限元模型,采用滞后阻尼理论来表示了组合结构等效阻尼比,并与实测数据进行对比.
结构等效阻尼比的表达式由黄本才[11]推导,他借用复频率(即无阻尼的自振频率)和阻尼比关系导出了实数范围内计算组合结构各阶等效阻尼比的表达式.该方法从滞后阻尼理论出发,首先推导出了计算组合结构体系复频率的表达式,然后用一个等效阻尼系数γe表示了等效之后的组合结构体系的复频率表达式,最后假定等效前后的组合结构体系的复频率相等,就可得等效阻尼比:
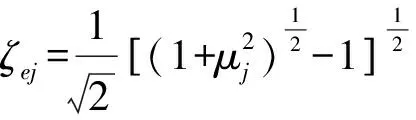
(12)
按泰勒级数展开,取前项
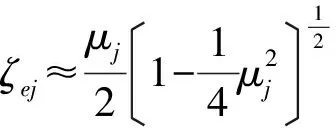
(13)
或者
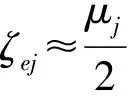
(14)
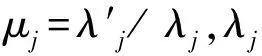
四周固支薄铝板有限元模型如图6所示,图6中铝板四周颜色较深的为补片.仿真的流程是:通过滞后阻尼理论计算了结构的等效阻尼比,然后返回有限元模型,再对结构进行随机振动分析得到了结构危险点的功率谱密度,使用Dirlik方法取得概率密度函数,通过Miner线性损伤累积准则计算结构的随机振动疲劳寿命.有限元仿真的流程如图7.

图6 修补后的薄铝板有限元模型
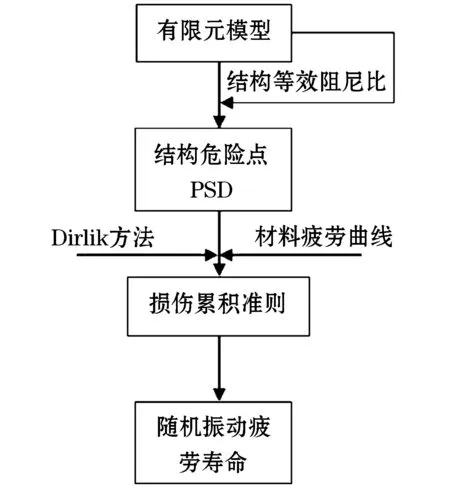
图7 振动疲劳寿命仿真计算流程图
模型中薄铝板的几何参数为l=300 mm,b=300 mm,h=1.8 mm,黏弹阻尼层共固化复合材料补片的几何参数为l=120 mm,b=40 mm,h=1.62 mm,其中厚度方向上阻尼层厚0.5 mm,嵌在碳纤维层之间.阻尼层上下面的碳纤维层各4层,单层的厚度为0.14 mm.碳纤维复合材料补片的几何参数与共固化补片相比,只是未嵌入阻尼层.为了模拟实验中胶层的影响,在仿真时补片最底层加入了一层0.25 mm厚刚度较大的壳单元.
碳纤维树脂基复合材料的性能参数如下:E11=125 GPa,E22=10.3 GPa,G12=4.3 GPa,υ12=0.29,ρ=1 635 kg/m3.阻尼参数为γ11=0.45%,γ22=4.22%,γ12=7.05%,γ23=γ13=γ12,γ22=γ33.阻尼材料的滞后阻尼系数γ=1.2,铝合金板取0.012.输入的随机谱为宽带平直谱,频率范围从150~450 Hz,大小为2.5 g2/Hz.
一阶固有频率和阻尼比的计算结果如表1所示.对比实验值,有限元模型计算的结果跟实验值比较接近,说明了仿真模型的可靠.分析误差的原因可能是实验中由于边界条件的影响,实测的固有频率会有误差;另外实际中粘胶剂的厚度没有那么均匀,仿真中是加入了一层均匀的壳单元,所以会造成一定的误差.
通过有限元的计算,可以很方便地得到结构各阶等效阻尼比值,在这里只取前两阶等效阻尼比作为返回有限元模型的参数.随机振动分析的RMISES应力云图如图8~10所示.从图中可以看到,没有补片的薄铝板应力集中区域在四边附近,而有补片的薄铝板应力集中转移到板的中央区域.对比修补前后,修补后的薄铝板MISES应力的均方根值最大值比修补前降低了46.34%.同时,根据图7的流程计算了结构的随机振动疲劳寿命,计算的结果如表2所示.

图8 无补片薄铝板RMISES应力云图,最大RMISES为66.55MPa

图9 碳纤维复合材料补片—薄铝板RMISES应力云图,最大RMISES为39.13MPa

图10 共固化补片—薄铝板RMISES应力云图,最大RMISES为35.71MPa
表2中可以看到,3#件的振动疲劳寿命最大,远远大于未修补件的寿命.同时寿命也大于碳纤维复合材料补片修补的结构件.仿真的结果表明,黏弹阻尼层共固化复合材料对结构件的修补作用很有效.
3.3 阻尼层厚度和补片长度的影响
下面将讨论当补片的参数变化时,对结构等效阻尼比和振动疲劳寿命的影响.如图11,研究了当阻尼层厚度或者补片长度变化时,对结构一阶等效阻尼比的影响.首先考虑当补片长度一定时,如当补片长为120 mm时,结构的等效阻尼比随着阻尼层厚度不同而变化的情况.其次计算了同一阻尼层厚度下, 120、160、200 mm三个不同长度补片修补下的结构一阶等效阻尼比.
表2结构件的振动疲劳寿命

结构件固有频率等效结构阻尼比f1/Hzf2/Hzζ1/%ζ2/%MISES应力的均方根/MPa振动疲劳寿命/s1#件184.67376.930.64520.643266.5516702#件226.42433.450.87440.849139.131.54×1053#件204.20400.321.18711.029335.714.47×105
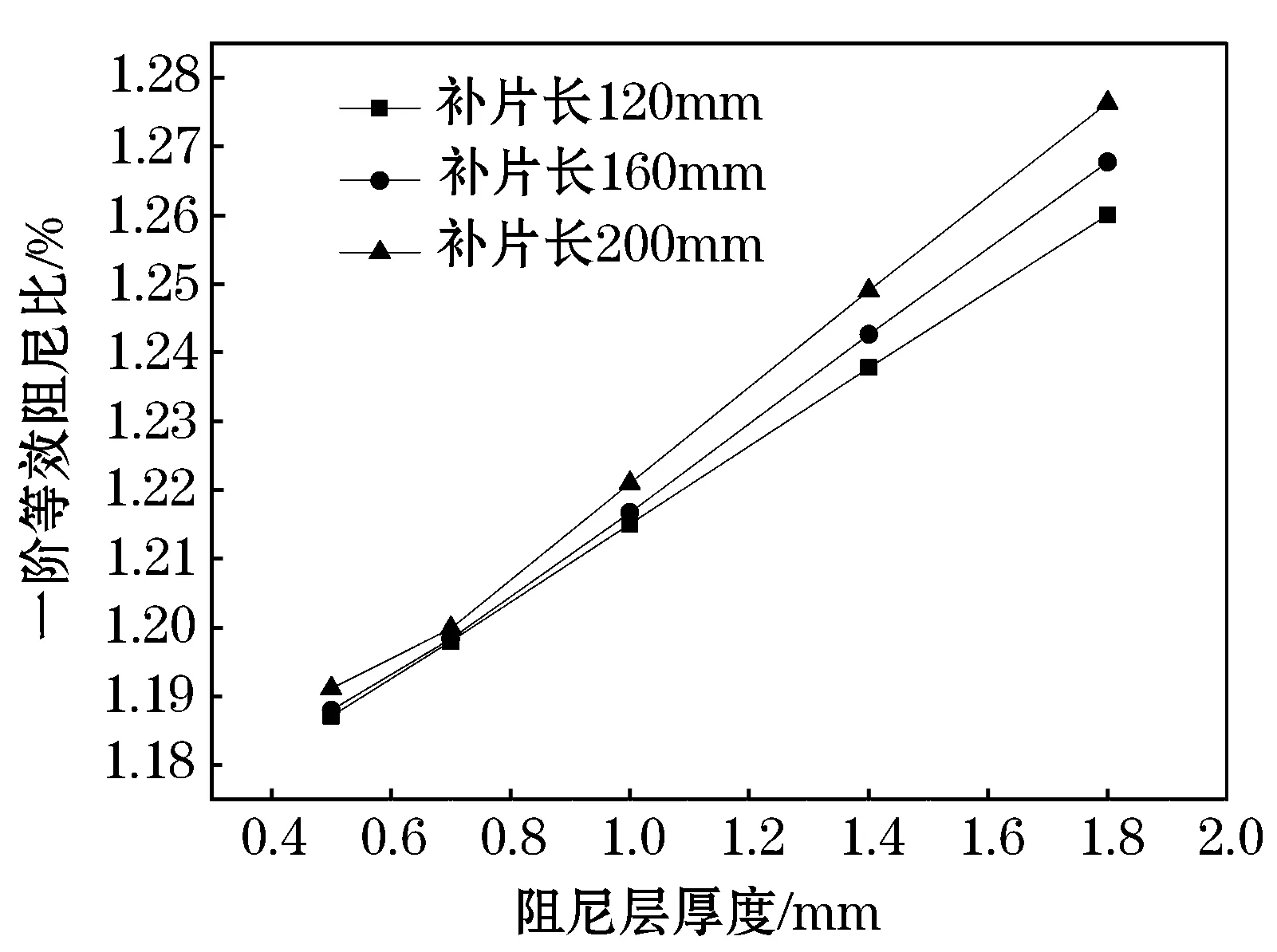
图11 阻尼层厚度对一阶等效阻尼比的影响
从曲线的走势可以看到,结构的等效阻尼比随着阻尼层厚度增大而增大.同时当阻尼层厚度一定时,补片长度越长可以提高结构阻尼比,这是因为补片长度增加后相当于提高了修补的面积,一定程度上起到了增大阻尼的作用.图12是在得到结构件的等效阻尼比之后,按照图7的计算流程估算得到结构的振动疲劳寿命.从图12中可以看到当补片长度一定,增加补片的阻尼层厚度可以提高结构件的振动疲劳寿命.而当补片长度变长,对振动疲劳寿命的影响有限,这是因为当补片超过120mm,修补的面积覆盖到应力较小的区域,多余出来的修补面积对降低应力效果不明显.所以在选择补片长度时,以可以完全覆盖应力集中区域为标准.
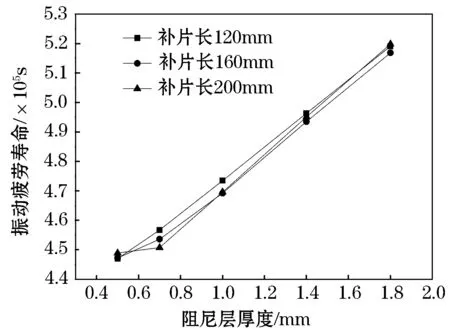
图12 阻尼层厚度对振动疲劳寿命的影响
以上是考虑了阻尼层厚度和补片长度对结构振动疲劳寿命的影响,通过计算的结果可以知道增加阻尼层厚度可以提高结构振动疲劳寿命,同时,当补片长度超过应力集中区域的长度时,修补效果不明显.
3.4 纤维增强复合材料的影响
纤维增强复合材料高强度和刚度的优点极大地改善了结构件补强区域的应力集中,考虑到纤维层厚度对振动疲劳寿命的影响,本文探讨了在相同厚度阻尼层、补片长宽和相同修补位置情况下,碳纤维层厚度对振动疲劳寿命影响的大小.
从图13中可以看到随着碳纤维层层数的增加,结构的一阶等效阻尼比降低.分析认为由于碳纤维层的刚度远远大于阻尼层,当碳纤维层层数增加时,会加速弱化阻尼层的阻尼效果,但是并不是碳纤维层层数越少越好.在图14中,当碳纤维层上下各2层时,对比其他的层数,虽然结构等效阻尼比是最大的,但是振动疲劳寿命却最低.这是因为纤维层是补片提供刚度和强度的主体,当纤维层减少时,会降低修补的效果.而当碳纤维层上下层数各为4层时,即上下层的厚度分别与阻尼层厚度基本一致时,结构的振动疲劳寿命达到最大.这说明在选择补片的几何参数时,结构等效阻尼比不是越大越好,而是有一个最优解.在这个结构阻尼比条件下,结构的振动疲劳寿命才能达到最大值.
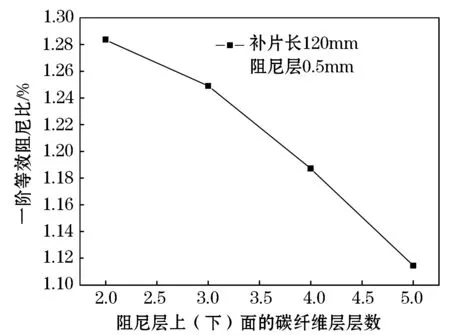
图13 碳纤维层层数对一阶等效阻尼比的影响
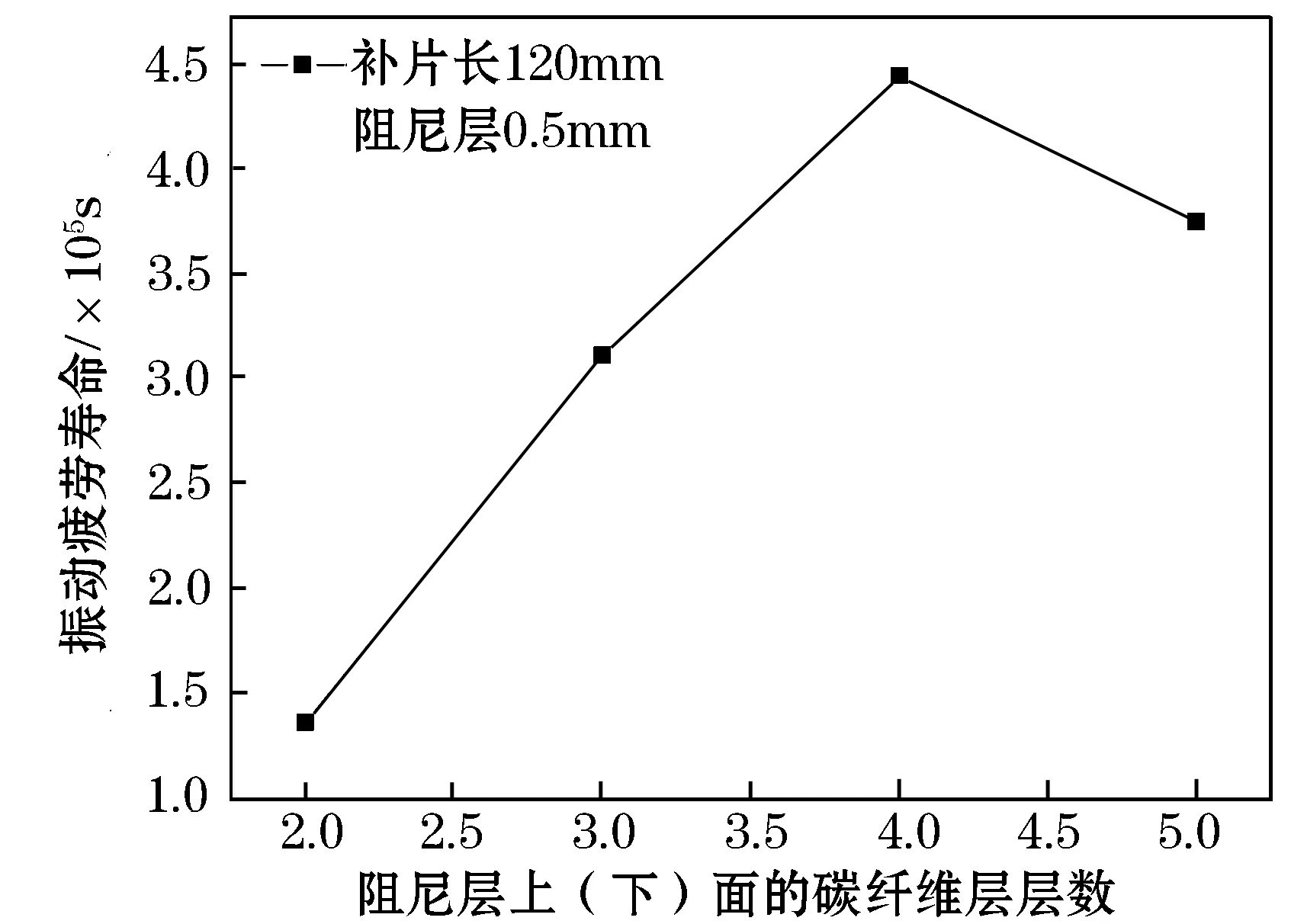
图14 碳纤维层层数对振动疲劳寿命的影响
4 结 论
1)利用滞后阻尼理论来计算组合结构的等效阻尼比表明,黏弹阻尼层共固化复合材料可以有效地提高薄壁结构的阻尼效果.
2)纤维增强复合材料补片和黏弹阻尼层共固化复合材料补片均可以调高薄壁结构的随机振动疲劳寿命,黏弹阻尼层共固化复合材料补片的预修补效果更好.
3)黏弹阻尼共固化复合材料的阻尼层越厚,有利于提高修补件的等效结构阻尼比和随机振动疲劳寿命.在制备复合材料阻尼结构补片时,补片的长度以完全覆盖应力集中区域为标准.同时,上下碳纤维层的厚度以达到阻尼层厚度为最佳,此时修补件具有最大的随机振动疲劳寿命.
参考文献:
[1] 姚起航, 姚 军. 工程结构的振动疲劳问题[J]. 应用力学学报,2006, 23(1):12-15.
[2] 刘文光,陈国平,贺红林,等. 结构振动疲劳研究综述[J]. 工程设计学报,2012,19(1):1-8.
[3] 潘利剑, 张博明, 戴福洪. 黏弹阻尼层共固化复合材料的阻尼特征分析[J]. 振动与冲击, 2009, 28(4):10-13.
[4] 张少辉, 陈花玲. 共固化复合材料黏弹阻尼结构的损耗因子研究[J]. 航空材料学报,2005, 25(1):53-57.
[5] 张忠胜, 梁 森. 嵌入式中温共固化复合材料阻尼结构制作工艺及层间结合性能[J]. 航空学报,2013, 34(8):1972-1979.
[6] 杨孚标, 肖加余, 黄学兵, 等. 含中心裂纹铝合金板复合材料单面胶接修复后的疲劳特性[J]. 宇航材料工艺,2008, 1:56-59.
[7] 陈礼威, 章向明.含孔洞钢板复合材料修复疲劳寿命数值分析[J]. 海军工程大学学报, 2008, 20(3):36-39.
[8] 孟彩茹, 卢博友. 基于PSD的随机载荷下振动疲劳寿命估算[J]. 机械设计,2009, 26(5):73-75.
[9] 曹明红, 邵 闯, 齐丕骞. 宽带随机振动疲劳寿命的频域分析与试验对比研究[J]. 机械科学与技术, 2013, 32(6):839-844.
[10] 李 晖, 孙 伟, 张永峰,等. 悬臂薄板结构阻尼特性几种测试方法的比较[J]. 中国工程机械学报, 2013, 11(4):347-353.
[11] 黄本才. 组合结构振动的等效阻尼比[J]. 上海力学, 1998, 19(2):141-145.
