氧等离子体平均离化度随温度、密度的变化关系

王 君, 方 敏

(四川理工学院 理学院,四川 自贡 643000)

0 引言

氧等离子体广泛存在于自然界和多种人造极端物理环境中,如星际物质中及在受激光作用的含氧物质表面.这些氧等离子体从温度到密度都有相当大范围的跨度,因此,其热力学性质也有着很大区别.对氧等离子体来说,重要的是对其高温辐射性质的研究[1-3],它包含两方面主要内容:一方面,通过对等离子体平衡状态和原子过程的研究得到相应热辐射性质，如发射光谱和双电子复合伴线等.另一方面，由于氧为低Z元素,其能级分裂明显,许多细致的研究已表明可以通过对比其发射光谱来找到相应离子及浓度，从而可对其温度进行诊断[4-5].但对于在何种温度、密度下等离子体有着怎样的离子分布状态,目前还没有系统的研究.上述两方面都表明等离子体的平衡状态对氧等离子体的研究十分关键.由于平均离化度是等离子体离化平衡的重要标志，因此，系统研究温度、密度与平均离化度的关系及变化趋势十分重要.在理论计算中，对离子状态的准确计算依赖于模型的正确选取和合理简化.

目前，对等离子体离化度的计算主要有局域热动平衡(LTE)模型[6-7]、日冕模型[8-9]和碰撞辐射模型[10-12]等.由于采用局域热动平衡或者日冕平衡来描述等离子体平衡状态均存在较大局限性,因此，本文对于温度不太高、密度不太低的氧等离子体平衡状态采用了广泛使用的碰撞辐射模型(CRM)来处理，并对模型进行了合理的简化,仅考虑碰撞离化、辐射复合、三体复合以及双电子复合过程.在此基础上采用稳态近似得到平衡方程,并计算了不同温度、密度下的离子分数分布,给出了对应的平均离化度,为等离子体温度诊断提供了有用数据.

1 理论模型与计算方法

对于温度不太高、密度不太低的等离子体,如采用日冕模型,自由电子密度增大使三体复合对占据数的影响逐渐明显,因此需修改日冕模型.加入三体复合过程,其可演变为碰撞辐射模型.这种模型能较好地描述介于局域热动平衡模型和日冕模型所处理的极端条件之间的等离子体的状态分布.由各过程对占据数的贡献,仅考虑上述过程的平衡关系,则可得到简化后的碰撞辐射电离平衡方程[13]

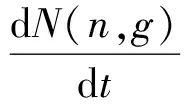
-N(n+1,g)Ne(α(Te,n+1,g)

+NeR3b(Te,n+1,g)+αDR(Te,n+1,g)),

其中Ne为电子密度，Te为电子温度,N(n,g)为离化度为n的离子基态占据数,S为碰撞离化率,α为辐射复合速率,R3b为三体复合速率,αDR为双电子复合速率.在稳态近似下,方程可写成如下形式:

由于计算跃迁系数十分困难[14-15],电离平衡的电荷态分布的计算使用了如下平均速率系数和经验公式[16-20]:

其中ξ(n)为外壳层电子数,In为电离势,S(n),α(n),R3b(n+1)单位均为s-1.式中的双电子复合速率系数采用了如下Burgess-Merts经验公式[21]：

其中

E为激发能,f(k,j)是振子强度,Z是核电荷数,IH为H的电离能.

本文研究了温度在15～1 000 eV内,密度在0.001～1 g/cm3范围内的氧等离子体的离子分数分布和平均离化度.平均离化度采用了定义式

来计算，式中n(Z*)表示离化度为Z*的离子数，ne,ni分别表示体系的总自由电子数和总离子数.

2 计算结果与分析

2.1 能级计算结果

本文列出了部分类硼氧离子能级,我们使用全相对论Dirac-Fock方法的FAC程序与他人使用的Cowan程序得到的计算值[22]进行了比较，结果列于表1中.表中离子态(LSJ)列,前面括号内部分表示电子排布2s12p1的离子态；后面字母S,P和D表示总轨道角动量L分别为0,1和2,其左上坐标为2s+1,右下角小标为相应J值.将2P1/2(J=1/2)态令为基态,能量为零,表中其余态能量均为相对此态的能量差.

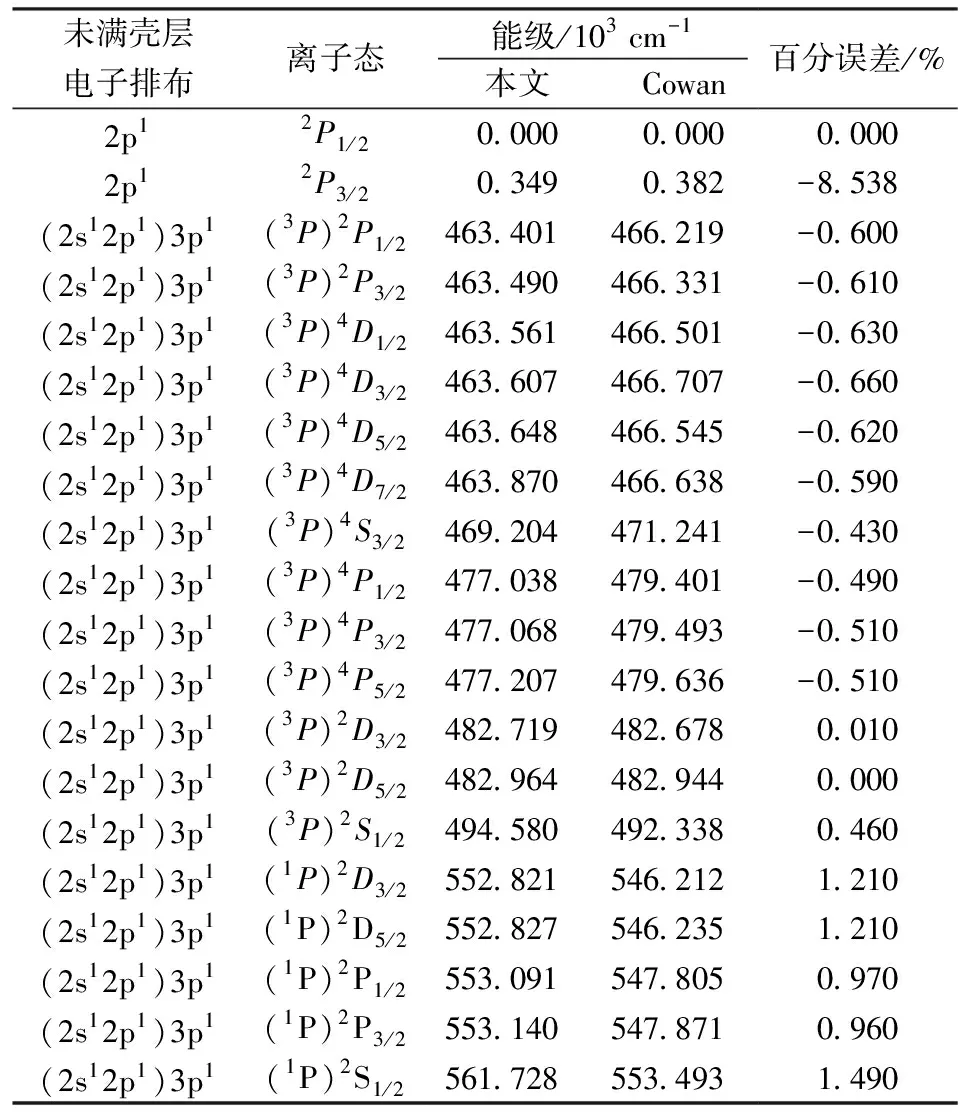
表1 部分类硼氧离子能级比较

两种程序得到的能量的百分误差列于表1中,可以看到除与基态相邻很近的态2P3/2(J=3/2)误差较大外,其余态的结果均符合得较好,主要误差集中在千分位上.这是由于2P3/2能量与我们设定的基态相当接近,此时误差较大,因而相对论Dirac-Fock方法比准相对论Hartree-Fock方法得到的结果更好[23].因此，我们将2P3/2态能量人为修正为Cowan程序计算的结果,而其余采用FAC的结果.

2.2 平均离化度结果及分析

图1，图2分别为密度0.001 g/cm3时氧等离子平均离化度随温度的变化及丰度分布图.

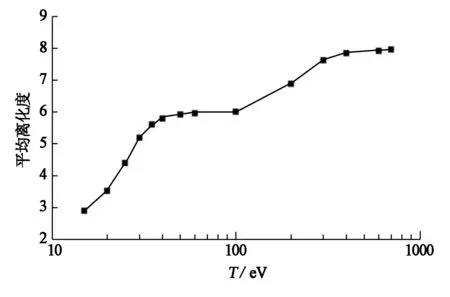
图1 密度为0.001 g/cm3时氧等离子体的平均离化度随温度的变化

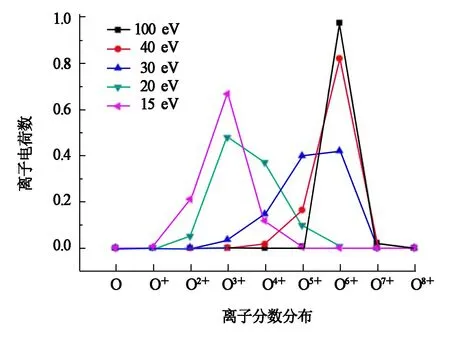
图2 密度为0.001 g/cm3时氧等离子体的离子丰度分布

由图1可以看出,在低温条件下,随着温度的升高,氧等离子体的平均离化度增大很快,当温度在35～100 eV时，曲线呈现出一个平台形状,增加温度基本没有改变平均离化度的数值，表明此时温度对平均离化度基本不产生影响.随着温度进一步升高,在100 eV以后，平均离化度又迅速增长，当温度达到400 eV左右时,O已基本被完全离化.结合图2,可以看到温度在15～20 eV范围内,等离子体内主要为O3+，其它离子占少部分，随着温度的升高,丰度分布图上可以看到峰值右移明显，说明温度对离化平衡影响很大,主要离子种类上也产生了很大变化.在35～100 eV范围内等离子体的主要丰度集中在O6+附近，这是由于O6+为类氦电子结构,其结构稳定,与类氢离子间有较大的电离势差.

图3对比了离子密度分别为0.001,0.01,0.1，1 g/cm3的氧等离子体体系平均离化度与等离子体温度的变化关系.

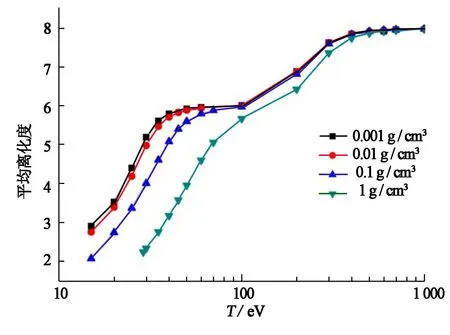
图3 不同离子密度时,平均离化度随温度的变化

可以看出,随着温度的增加,不同离子密度等离子体的平均离化度增大呈台阶状,其总体趋势基本一致.当离子密度相当大时,由于碰撞效应明显占主导,其能量交换迅速,台阶特征逐渐消失.同一温度下,密度低的等离子体平均离化度较大.

图4对比了不同温度下平均离化度随离子密度的变化趋势.

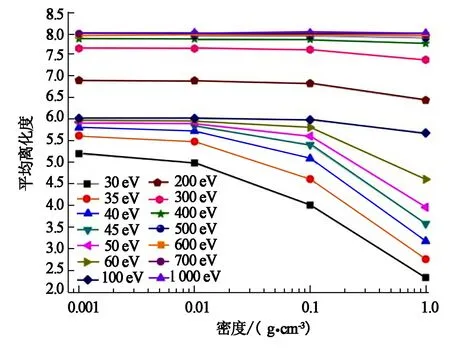
图4 不同温度时,平均离化度随离子密度的变化

由图4可知，离子密度小于0.01 g/cm3时,其平均离化度几乎不随离子密度变化,当离子密度较大时则平均离化度随离子密度增大而减小.其原因为当离子密度较小时,辐射为主要能量传递方式,此时密度对平均离化度的影响几乎可以忽略.而离子密度较大时,碰撞为主要方式,则离子密度对平均离化度影响较大.还可以看出,低温时平均离化度减少趋势高于高温等离子体.也就是说高温下等离子体平均离化度几乎不随等离子体密度变化.综上所述,等离子体温度是影响等离子体平均离化度的重要因素,而稀薄等离子体以及高温稠密等离子体平均离化度几乎不随离子密度变化,低温稠密等离子体平均离化度则随等离子体密度增大而减少,且随温度升高而逐渐不随密度变化.

3 结论

本文使用全相对论Dirac-Fock方法计算了氧原子能级,对误差较大的低能级做了能量修正,得到了较好能级的结果.在此基础上采用了碰撞辐射模型计算了温度在15～1 000 eV内,密度在0.001～1 g/cm3范围内的氧等离子体的平均离化度.相同密度下,平均离化度随等离子体温度增加而增大,到一定温度时出现台阶状,随后继续增大至完全电离.其台阶特性随等离子体密度增大而逐渐减小直至消失.在同一温度下,密度越小,等离子体平均离化度越高.温度是影响等离子体平均离化度的重要因素,密度低于0.01 g/cm3的稀薄氧等离子体以及100 eV以上的氧等离子体平均离化度几乎不随离子密度变化,100 eV以下并且密度高于0.01 g/cm3的氧等离子体平均离化度则随等离子体密度增大而显著减少,且随温度升高而逐渐不随密度变化.

参考文献:

[1] Cauchon D L.Radiative heating results from the FIRE Ⅱ fight experiment at a re-entry velocity of 11.4 km/s[R].Hampton,VA:NASA Report TMX-1402,1967.

[2] Lamet J M,Bahou Y,Riviere P,et al.Radiative transfer in gases under thermal and chemical nonequilibrium conditions:application to earth atmospheric re-entry[J].J Quant Spectrosc Ra，2008,109(2):235.

[3] Lamet J M,Riviere P,Perrin M Y,et al.Narrow-band model for nonequilibrium air plasma radiation[J].J Quant Spectrosc Ra，2010,111(1):87.

[4] Cauchon D L,Mckee C W,Coenette E S.Spectral measurements of gas-gap radiation during FIRE flight experiments at reentry velocities near 11.4 km/s[R].Hampton,VA：NASA Report TM X-1389,1967.

[5] Mazoué F,Marraffa L.Determination of the radiation emission during the FIRE Ⅱ entry[C].Proceedings of the 2nd International Workshop on Radiation of High Temperature Gases in Atmospheric Entry.Rome:6-8，September，2006.

[6] Drawin H W,Felenbok P.Data for plasma in local thermodynamic equilibrium[M].Paris:Gauthier-Villars,1965.

[7] Aller L H.Astrophysics—the atmospheres of the sun and stars[M].2nd ed.New York:Ronald Press,1963.

[8] Hahn Y.Generation of very high harmonics of optical radiation in rare gases[C].New York:AIP Conference Proceedings,1990,205:550.

[9] Bitter M,Hsuan H,von Goeler S,et al.Measurements of dielectronic recombination rate coefficients for He-like and H-like metal mons from tokamak plasmas[J].Phys Scr，1991,T37:66.

[10] Fujimoto T.A collisional-radiative model for helium and its application to a discharge plasma[J].J Quant Spectrosc Ra，1979,21(4):439.

[11] 李晶,谢卫平,黄显宾,等.“碰撞-辐射”模型在Z箍缩等离子辐射谱分析中的应用[J].物理学报，2010,59(11):7922.

[12] Bultel A,van Ootegem B,Bourdon A，et al.Influence of Ar2+in an argon collisional-radiative model[J].Phys Rev E，2002,65:046406.

[13] 张红,程新路,杨向东,等.金等离子体平均离化度随温度变化关系的研究[J].物理学报，2003,52(12):3098.

[14] 焦荣珍,程新路,杨向东,等.类镍Dy38+离子的双电子复合速率研究[J].物理学报，2002,51(8):1755.

[15] 易有根,郑志坚,颜君,等.Au激光等离子体的双电子复合速率系数[J].物理学报，2002,51(12):2740.

[16] Gupta G P，Sinha B K.Parametric dependence of X-ray laser gain in laser plasmas for 3p-3s transitions in neon-like krypton ions[J].J Appl Phys，1995,77(6):2287.

[17] 王泰春,王玉芝.几个到十几个电子的原子电离的弛豫过程[J].原子与分子物理学报，1986(3):231.

[18] 王泰春,纪文贵,姚军,等.多电子原子的电离过程[J].原子与分子物理学报，1986(3):219.

[19] Colombant D，Tonon G F.X-ray emission in laser-produced plasmas[J].J Appl Phys，1973,44(8):3524.

[20] 张钧,古培俊.计算局部热动平衡和非局部热动平衡等离子体电离度的近似方法[J].计算物理，1987(1):1.

[21] Merts A L,Cowan R D，Magee N H.The calculated power output from a thin ion-seeded plasma[R].Los Alamos:Los Alamos Scientific Laboratory Report LA-6220-MS,1976.

[22] Murakami I,Safronova U I,Vasilyev A A，et al.Excitation energies,radiative and autoionization rates,dielectronic satellite lines,and dielectronic recombination rates to excited states for B-like oxygen[J].Atomic Data and Nuclear Data Tables,2005,90(1):1.

[23] Gu M F.The flexible atomic code[J].Can J Phys,2008,86(4):675.