带五次项的非线性Schrödinger方程的一个紧致差分格式

初日辉

(南京航空航天大学 理学院,江苏 南京 211100)

0 引言

带五次项的非线性Schrödinger方程是一个重要的数学物理模型,它在诸如非线性光学、等离子物理等方面有着广泛的应用[1]．关于带五次项的非线性Schrödinger方程的数值研究有很多,如有限差分法、有限元法、有限体积法等,其中有限差分法以其简单、实用等优点被广泛使用．最近,关于偏微分方程的高精度紧致差分格式研究是国际上的一个热点[2-3].基于此,本文考虑如下的带五次项的非线性Schrödinger方程:

iut+uxx-(|u|2+|u|4)u=f(x,t)u, (x,t)∈(a,b)×(0,1),

(1)

u(x,0)=u0(x),x∈(a,b),

(2)

u(0,t)=u(1,t)=0,t∈(0,T],

(3)

其中u0(x)为已知的复函数,f(x,t)和u(x,t)分别是实值和复值函数，i为虚数．经过简单的计算可得该问题的电荷和能量满足如下的关系:

(4)

(5)

其中Q(t),E(t)分别称为某时刻的电荷和能量,而Q(0),E(0)则分别称为初始时刻的电荷和能量,(4)式表示的是电荷守恒．

对于本文研究的方程,张鲁明等[4]构造了一个差分格式,并证明方程的收敛阶为O(τ2+h2)．王询等[5]提出一个五点四阶的差分格式．但对于带五次项的非线性Schrödinger方程的紧致差分格式,目前未发现相关文献．本文的目的是提出一个紧致差分格式,使得收敛阶达到O(τ2+h4),并通过理论和数值实验验证格式的正确性．

1 相关符号的定义

本文中使用的记号如下:

xj=a+jh,tn=nτ,j=0,1,…，J;n=0,1,…,N,

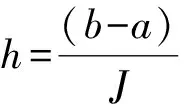
定义三对角矩阵

注意到矩阵H是一个对称正定矩阵,因此存在一个对称正定矩阵M,使得M=H-1．

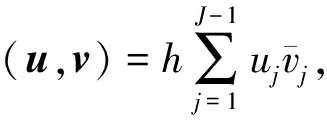
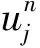
2 差分格式及其解的估计

2.1 差分格式的建立

通过大量的数值试验可知,非守恒的格式在计算中容易出现非线性“爆炸”[4],守恒的格式能较好地完成计算．基于此,提出如下的差分格式:

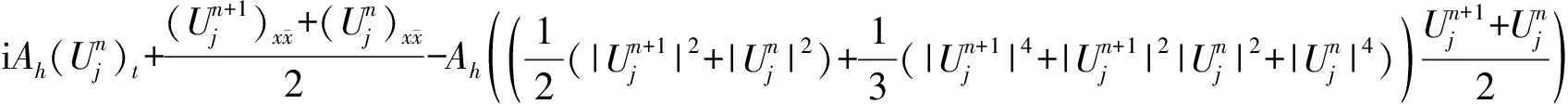
(6)

(7)

(8)

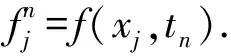
设

则(6)式可变为

(9)

为了计算方便,方程(9)可等价写成如下的向量形式:

(10)

2.2 差分格式解的估计

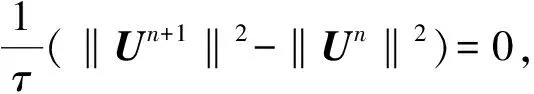
Qn=Qn-1=…=Q0.

(11)

将(10)与Un+1-Un做向量内积,运用Cholesky分解,取实部得

其中M=RTR.

令

则

将上式两端对n求和得

(12)

其中Qn,En分别称为离散电荷与离散能,(11)和(12)式分别为(4)和(5)式的数值模拟.基于以上的讨论得到定理1．

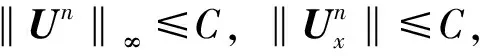
证由(11)式可得

‖Un‖≤C,

(13)

由(12)和(13)式可得

根据Sobolev不等式可知‖Un‖∞≤C. 证毕.

3 差分格式的稳定性和收敛性

定理2假设u(x,t)∈C6,3，并且满足定理1的条件,则差分格式(7)，(8)和(10)式依平方模连续地依赖于初始条件与f(x,t).

证设精确解un满足

(14)

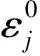
(15)

将(15)式的两端与en+1+en做内积,然后取虚部得

(16)

其中

(16)式的第1项为

(17)

(16)式的第2项为

(18)

(16)式的第3项为

(19)

(16)式的第4项为

(20)

(16)式的右端项为

(21)

结合(17)～(21)式,并两端对n求和,得

(22)

根据定理1,有

≤C(‖en+1‖2+‖en‖2).

(23)

同理可得

|I2|≤C(‖en‖2+‖en+1‖2),

(24)

≤C(‖δFn‖2+‖en+1‖2+‖en‖2),

(25)

将(23)～(25)代入(22)式，有

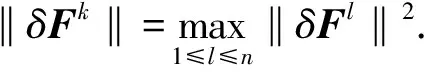
类似地，可以证明差分格式的解依平方模收敛到方程的解．

4 数值实验

考虑如下一个具体算例,取

f(x,t)=4(x-2t)2-exp(-2(x-2t)2)-exp(-4(x-2t)2),

u0(x)=exp(-x2+ix).

这时有孤波解u(x,t)=exp(-(x-2t)2+i(x-3t)).

运用上述提出的差分格式(7),(8)和(10)式对此算例进行求解,取计算区间为[-15,15]．首先验证格式的收敛阶,这里分别取h=0.025,0.05,0.1,0.2,τ=h2,T=1,从图1中可以很明显看出差分格式(7)的收敛阶为O(τ2+h4),图2绘出了在τ=0.01时数值解的图像,数值实验说明了理论证明的正确性．

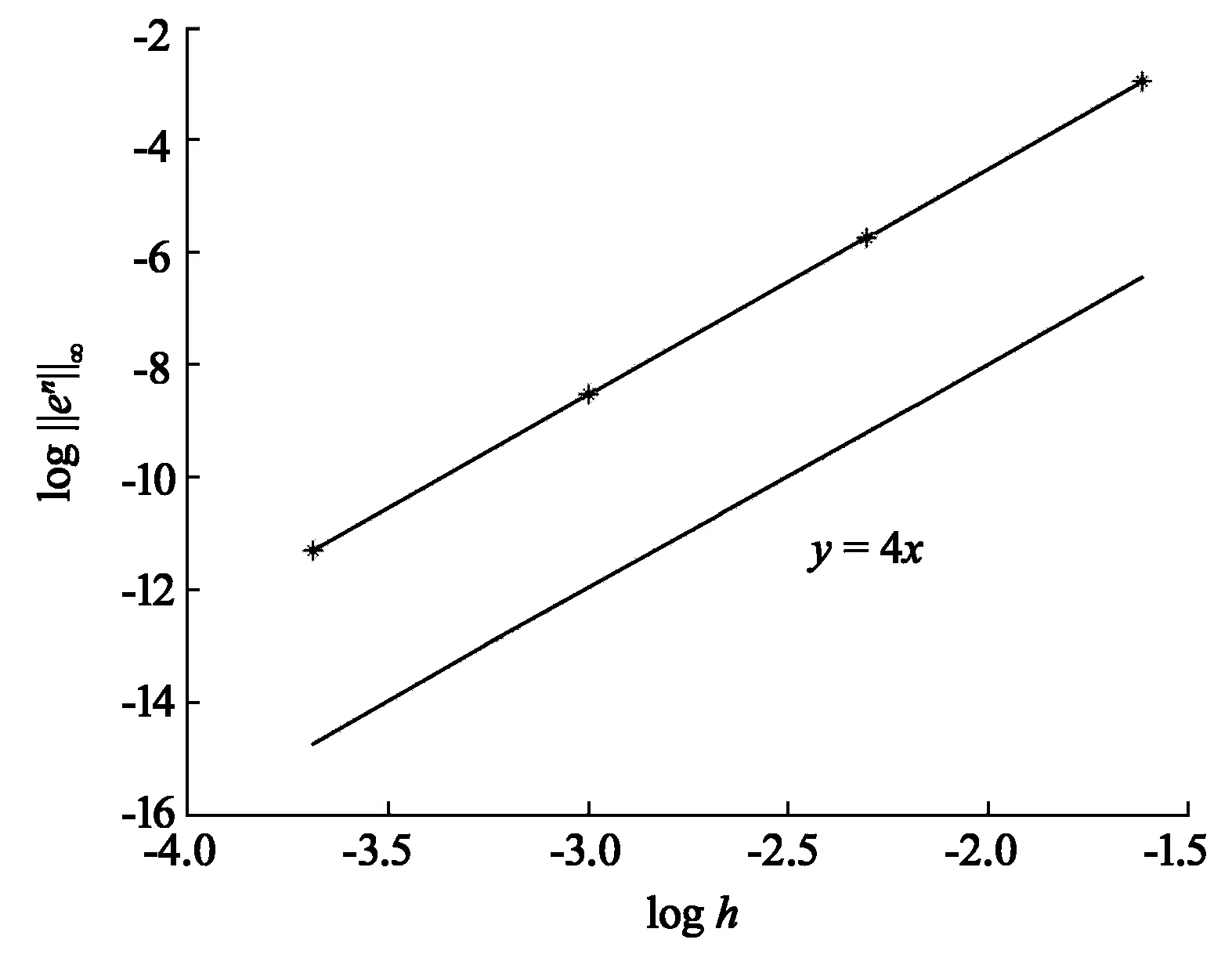
图1 τ=h2时差分格式的收敛阶

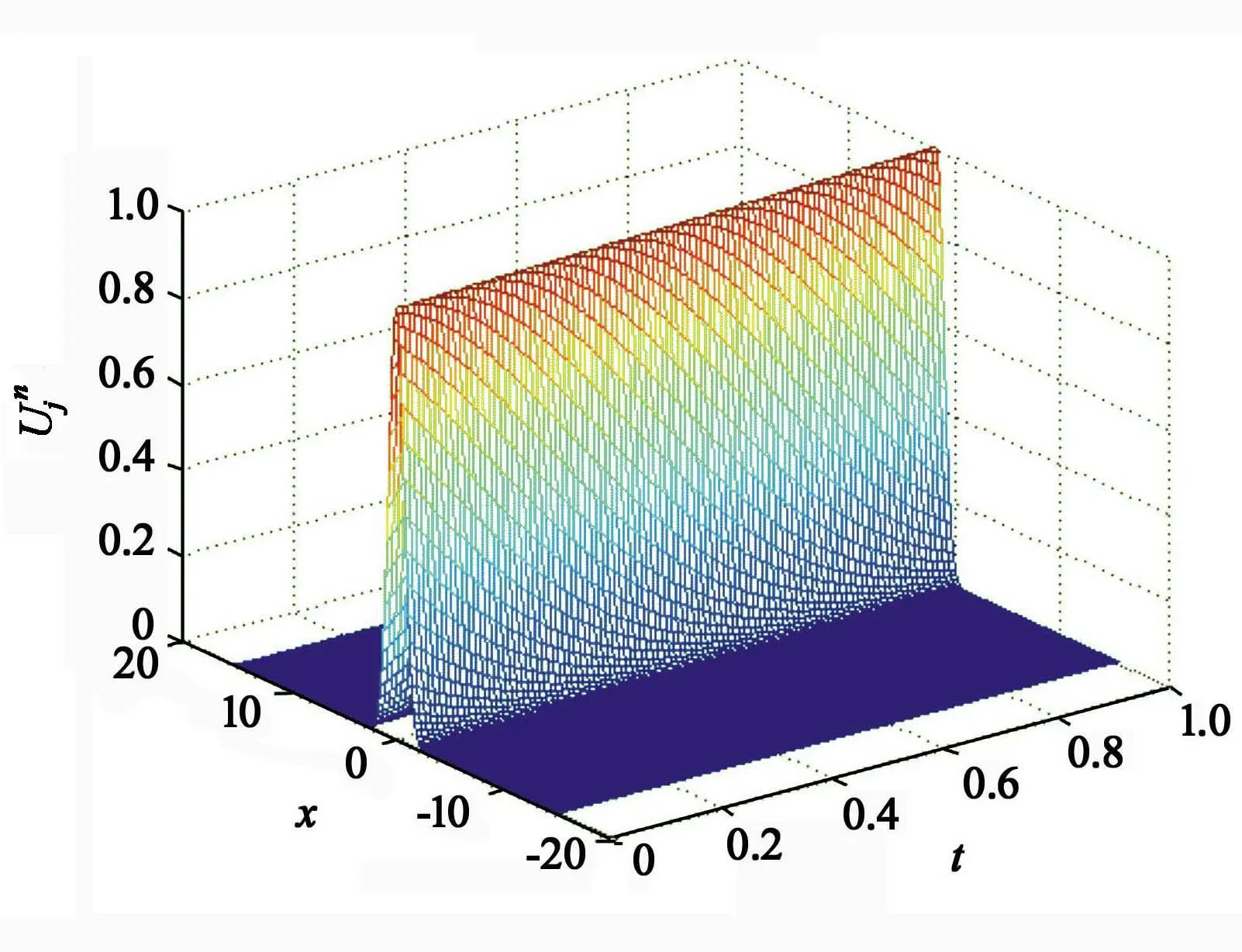
图2 τ=0.01时对孤波解的数值模拟

5 总结

本文对带五次项的非线性Schrödinger方程给出了一个紧致差分格式,从数值上模拟了Q(t)和E(t)，并利用能量的方法证明了该差分格式的稳定性和收敛性,数值实验的结果很好地验证了理论的证明．

参考文献:

[1] Abdullaev F K,Salerno M.Gap-Townes solitons and localized excitations in low-dimensional Bose-Einstein condensates in optical lattices[J].Phys Rev A,2005,72(3):033617.

[2] 王廷春，郭柏灵.一维非线性Schrödinger方程的两个无条件收敛的守恒紧致差分格式[J].中国科学：数学，2011,41(3):207.

[3] Hu X,Zhang L.A compact finite difference scheme for the fourth-order fractional diffusion-wave system[J].Comput Phys Commu,2011,182(8):1645.

[4] 张鲁明,常谦顺.带五次项的非线性Schrödinger方程差分解法[J].应用数学学报,2000,23(3):351.

[5] 王询,曹圣山.带五次项的非线性Schrödinger方程新差分格式[J].中国海洋大学学报,2009,39(9):487.