基于ADAMS的焊接机器人逆运动学求解

2014-09-13谢黎明张秀林靳岚

机械制造与自动化 2014年5期

谢黎明张秀林靳岚

(兰州理工大学机电工程学院,甘肃兰州730050)

0 引言

机械手的逆运动学在机器人的运动学及轨迹规划中都是非常重要的课题，因机械手逆运动问题随着运动关节的增多而越来越复杂，要建立通用的算法相当困难。对逆运动方程求解提出了解析法[1]、几何法[2]、迭代法[3]、几何-解析法[4]以及一些新的解析法[5]；近年来，相继提出采用遗传算法[6]、神经网络理论[7]、遗传粒子群算法[8]、基于信赖域的优化算法[9]等。其中，Paul[10]、王奇志[1]等分别对PUMA560机器人在d2=0，d2≠0条件下的逆运动方程提出了相应的解析法。但此法在实际应用中要直接得到完全正确的8组逆解仍不是件易事，有时出现8组逆解中有几组不是真解。刘松国[3]等提出的迭代法的收敛速度要远高于其他算法，但由于受雅可比矩阵的制约，不一定能求解出工作空间所有可行点的逆解。王洪斌[7]采用神经网络理论求解逆运动，但由于神经网络结构对最终结果影响的不确定性及需要大量已知训练样本，使这一问题未能得到很好的解决。陈宁[5]提出了一种新的解析法，推导出直接计算各转角变量正、余弦值的公式，计算出各解的转角量，但运动方程中有许多角度的耦合，比如C234，这就使得无法从矩阵中提取足够的元素来求解单个的正弦和余弦项以计算角度。为使角度解耦，方便求解各角的正、余弦，本文针对PUMA560型焊接机器人进行运动学逆解分析，用单个或多个()-1矩阵左乘0A6矩阵，使得方程右边不再包括这个角度，于是就可以找到产生角度的正弦值和余弦值的元素，并进而求得相应的角度，完成运动学方程的求逆。

1 机器人的正运动学模型

机器人运动学的分析是机器人轨迹规划研究的基础，包括正运动学问题和逆运动学问题，其中逆运动学应用比较多，而正运动学数学模型的建立是运动学求逆的关键。所以，首先建立了机器人正运动学数学模型，以PUMA560为研究对象进行求解计算，用ADAMS软件仿真，并与计算结果相对比，验证了所建正运动学模型的正确性，为后续的运动学求逆奠定了基础。

1.1 正运动学分析

采用D-H方法[11]来表示此连杆坐标系与上一连杆坐标系之间的关系，相邻两连杆的空间关系矩阵为连杆变换矩阵。建立的齐次变换矩阵为:

式中:C=cos，S=sin，αi-1为zi-1到zi沿xi-1测量的距离；ai-1为zi-1到zi绕xi-1旋转的角度；di为xi-1到xi沿zi测量的距离；θi为xi-1到xi绕zi旋转的角度；xi，yi，zi为第i个关节的坐标系。

由上面的相邻连杆之间的变换矩阵，可以得出正运动学方程:

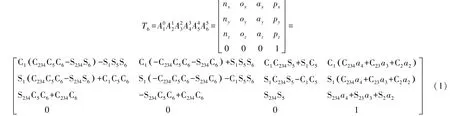
，，，，，为肩坐标系相对于基座坐标系、大臂坐标系相对于肩坐标系、小臂坐标系相对于大臂坐标系、腕1坐标系相对于小臂坐标系、腕2坐标系相对于腕1坐标系、腕3坐标系相对于腕2坐标系。

式中:为姿态矩阵；为位置矩阵；

C234——分别代表 cos(θ2+θ3+θ4)，S234为 sin(θ2+θ3+θ4)，余同。

1.2 PUMA560的正运动学计算

PUMA560机器人本体的关节结构由回转的机体、肩、大臂、小臂、腕部，机械手等部分组成(图1)，共有6个关节自由度，而且6个关节均为旋转关节，属关节型机器人。前3个关节主要影响末端执行器的位置，后3个关节决定末端的姿态。如图2所示POMA560机器人的杆件坐标，根据D-H方法由图2可以得出POMA560机器人的各杆件参数如表1所示。

图1 PUMA560的实体模

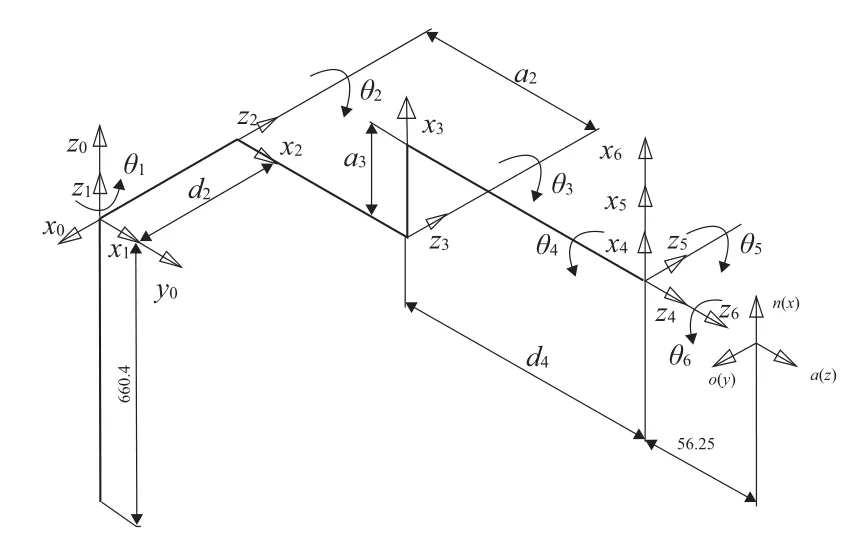
图2 PUMA560机器人的坐标

其中:a2=431.8 mm，a3=20.32 mm，d1=660.4 mm，d2=149.09 mm，d4=433.07 mm，d6=80.13 mm。

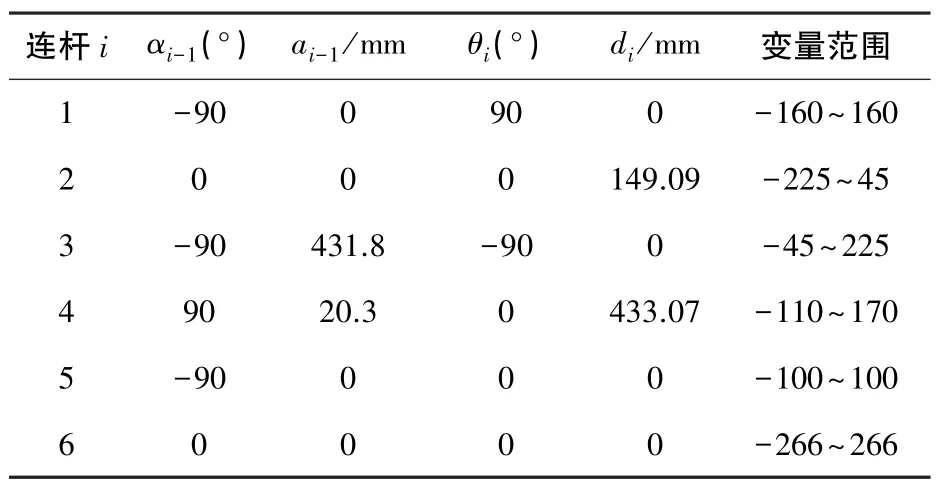
表1 PUMA560机器人的连杆参数表

其中:=

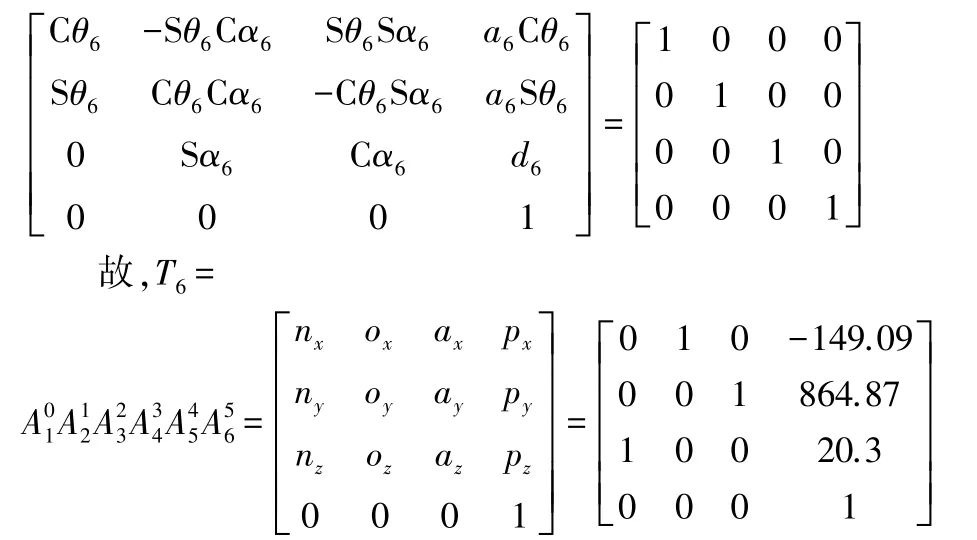
与图2所示的情况完全一致，则机械手末端相对于基座标的位姿[12]为:

则机械手末端在ADAMS世界坐标系中的位姿为:

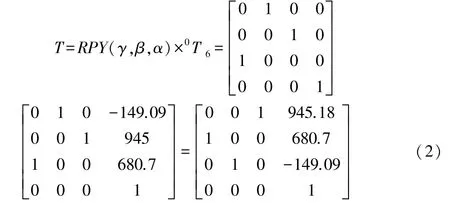
现让肩关节绕y轴旋转-90°，小臂关节绕x轴旋转90°，其他的关节不旋转，得到机械手末端在ADAMS世界坐标系中的位姿为:

1.3 PUMA560机器人运动学仿真

图3和图4分别表示POMA560机器人各杆件在仿真前、仿真后的位置关系。经过仿真得出机器人未端在整个运行过程中的位移曲线如图5所示。

从仿真结果可以看出，机械手末端在0 s时刻的坐标为(945，680，-149)，与式(2)的计算结果相近。机械手的末端在3 s时的坐标为(149，147，452)，与式(3)的计算结果相近。所以，验证了所建模型的正确性。

2 逆运动学分析

逆运动学算法是机器人轨迹规划的基础，但在求解时，运动方程中有许多角度的耦合，为使角度解耦，方便求解各角的正、余弦，本文用单个或多个()-1矩阵左乘0A6矩阵，使得方程右边不再包括这个角度，于是可以找到产生角度的正弦值和余弦值的元素，并进而求得相应的角度，完成运动学方程的求逆。

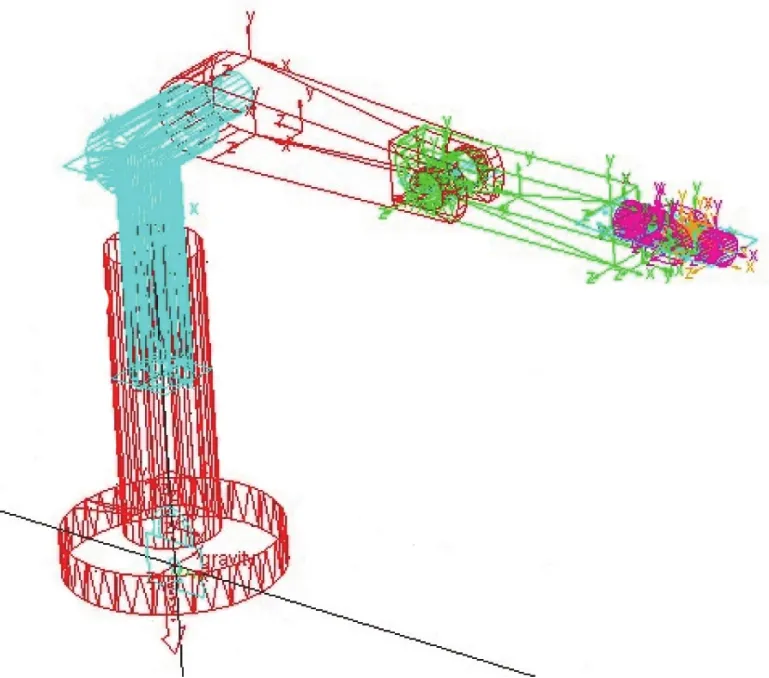
图3 仿真前各连杆之间位置关系

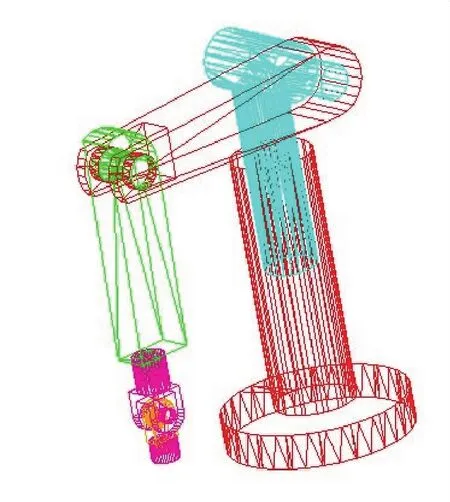
图4 仿真后各连杆之间位置关系

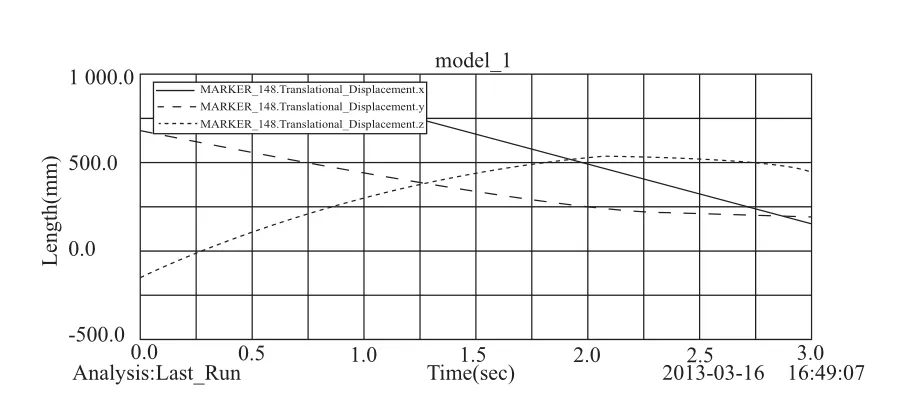
图5 末端的位移曲线

2.1 逆运动学方程的求解

根据上述得出的正运动学方程式(1)分析:

1) 求θ1

用()-1左乘式(1)两边，得到:

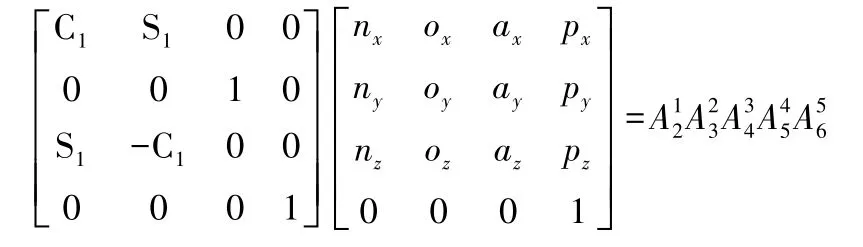
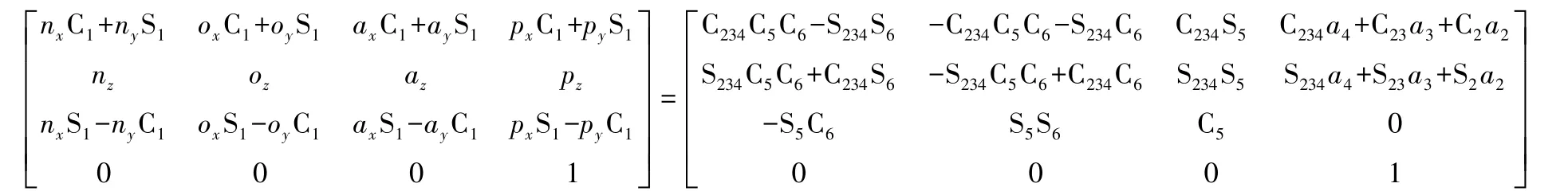
根据等式两边第3行第4列元素对应相等，有:

2)求θ3

根据式(1)两边第1行第4列和第2行第4列分别对应相等，有:

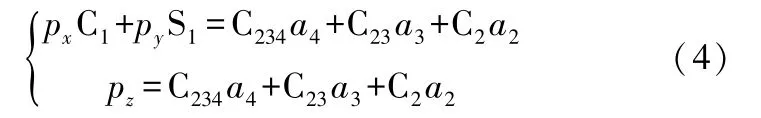
将两个方程两边平方相加，得:

式中， S2S23+C2C23=Cos(θ2+θ3-θ2)=C3

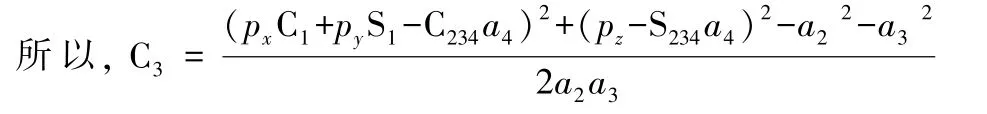
故

3)求解θ2，θ4

用左乘式(1)两边，得到:

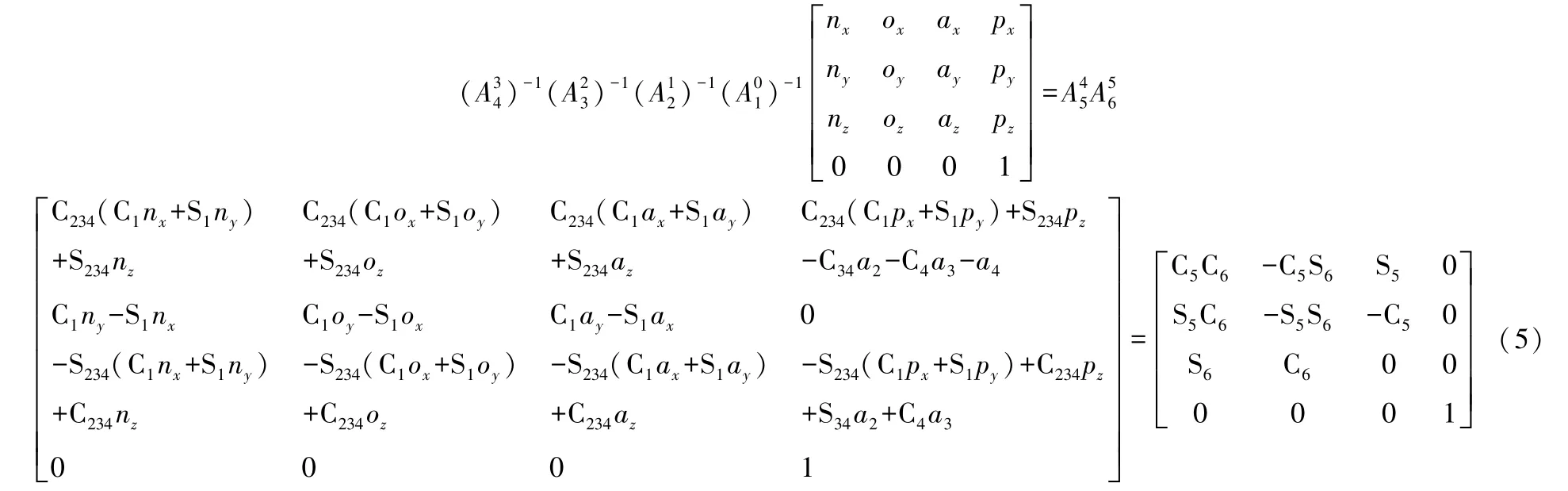
式(5)两边第3行第3列元素对应相等，有:

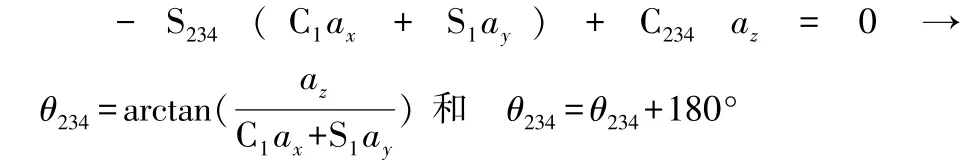
由此可以求得S234，C234，即可求得θ3

由式(4)可知

可得:

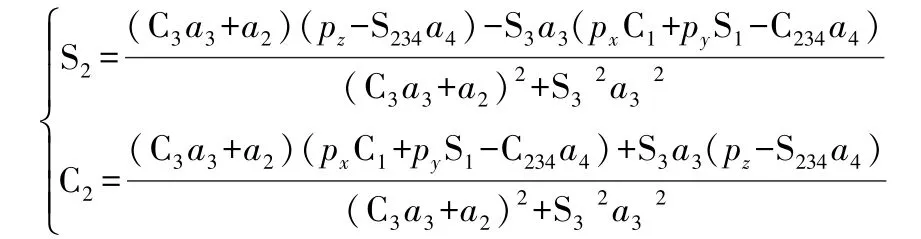
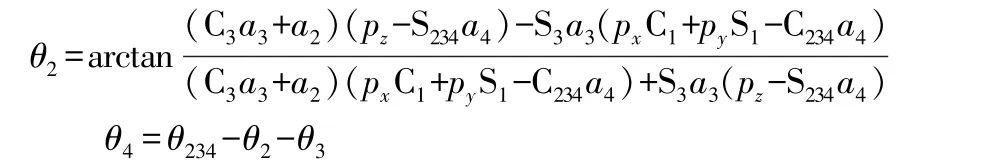
因为θ234有两个值，所以θ4也相应有两个值。

4) 求θ5

由式(5)两边第1行第3列和第2行第3列元素对应相等，有:

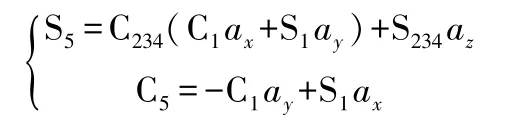
故

5) 求θ6:

由()-1左乘式(5)有:

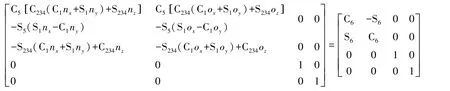
由第2行第1列和第2行第2列元素对应相等，得:

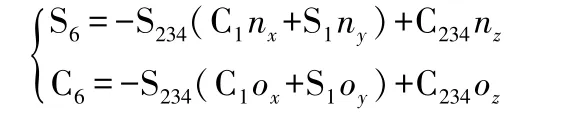
故

给定末端位姿为式(3)计算结果，根据上述所得各角求解公式，用MATLAB编程计算各关节对应的角度，计算结果为:θ1=90°，θ2=0°，θ3=-90°，θ4=0°，θ5=0°，θ6=0°，与表1所给条件相符，所以验证了逆运动学方程的正确。

3 结语

本文针对机器人运动学方程中的角度耦合问题，采用解析法推导了焊接机器人逆运动学方程。通过解耦，已给出各角求解公式，由求解公式可知PUMA560的运动反解可能存在8种解。但是，由于结构的限制，各关节变量不能全部在360°范围内运动，有些解不能实现，应根据一些约束条件选取其中最满意的一组，以满足机器人的工作要求。该算法使用于机器人的最后三个关节交于一个公共点，否则就不能用这个方法来求解，而只能直接求解矩阵或通过计算矩阵的逆来求解未知的量。大多数工业机器人都有相交的腕关节。

[1]王志奇，徐心和，尹朝万.PUMA机械手逆运动方程新的推导方法及求解[J].机器人.1998，2(20):81-87.

[2]Fu KS， Gonzalez RC，LeeCSG.Robotics Control Sensins Vision and Intelligence.McGraw-Hill，NewYork，1987.

[3]刘松国，朱世强，李江波.6R机器人实时逆运动学算法研究[J].控制理论与应用，2008，25(6):1037-1041.

[4]贺昱曜.机器人PUMA560逆运动方程的新解法[J].机器人，1987，3(3):19-26.

[5]陈宁，焦恩璋.PUMA机械手逆运动方程求解新方法[J].南京林业大学学报(自然科学版)，2003，27(4):23-25.

[6]刘永超，黄玉美，王效岳.基于遗传算法的机器人运动学逆解[J].机器人，1998，20(6):421-426.

[7]王洪斌，宋佐时，王宏瑞.基于模糊神经网络的机器人逆运动学问题[J].系统仿真学报，2002，7(14):852-858.

[8]吴振宇，姚明江，冯林，等.基于遗传粒子群的PUMA560机器人逆运动求解[J].计算机仿真，2011，28(10):173-176.

[9]马化一，张艾群，张竺英.一种基于优化算法的机械手运动学逆解[J].机器人，2001，2(23):137-141.

[10]Paul RP，Shimano BE，Mayer G.Kinematic Control Equations for Simple Manipulators.IEEETrans SMC，1981，11(6):449～455.

[11]李志辉，廖小平，林一忠，等.6R喷漆机器人的运动学分析及仿真[J].机械设计与制造，2010，4(4):176-178.

[12]蔡自兴.机器人学[M].北京:清华大学出版社，2000.