基于EEMD样本熵的电机轴承电流信号复杂性评估

楼军伟胡赤兵王季李贵子贾德强

(1.兰州理工大学 机电工程学院,甘肃 兰州730050；2.甘肃省机械产品检测与技术评价重点实验室,甘肃兰州730030)

滚动轴承各元件表面发生损伤时在运转过程中接触到损伤处轴心就会产生径向运动，使得电机定子和转子之间的气隙长度发生变化，从而导致气隙磁通变化，产生谐波磁通，在感应电压作用下定子电流中产生相应的电流谐波。文献[1，2]分别给出了各自的电流谐波频率与滚动轴承特征频率间的映射模型。然而定子电流信号是高集成度的、变化比较微弱的，在评估电流谐波出现的概率即电机定子电流信号复杂性时难度较大。近似熵、样本熵是信号复杂性评估算法，但它们均是在单一尺度上对信号进行分析的[3，4]，直接应用于定子电流信号分析时效果较差。而总体平均经验模态分解(ensemble empirical mode decomposition，EEMD)能对信号进行多尺度分解，不仅弥补了样本熵单一尺度分析的不足，而且改进了经验模态分解存在的模态混叠缺陷[5]。因此，文中将EEMD与样本熵结合来评估轴承定子电流信号复杂性，通过比较样本熵和EEMD样本熵在评估轴承不同损伤程度时定子电流信号复杂性的效果表明:EEMD样本熵的评估效果更好，并且其变化趋势与定子电流中电流谐波的变化趋势一致，该方法可应用于封闭装置电机轴承状态的监测和预判，也可以作为支持向量智能机故障识别的信号源。

1 定子电流信号的测取

实验中传感器用霍尔电流传感器，该传感器具有外围电路简单，检测灵敏度高，动态特性好等特点；信号调理为DBK45调理卡，输入电压范围-10 V～+10 V，巴特沃斯带通滤波；数据采集卡选用USB-6210信号采集卡，该卡具有16位输入，通道采样率250 ks/s，USB总线供电。在电机负载为1.45 kW，转速为1 500 r/min时用霍尔电流传感器测取驱动端滚动轴承(型号6205)正常，内圈单点点蚀、外圈单点点蚀、滚动体单点点蚀4种情况下的电机A相定子电流信号，经采集卡和信号调理卡后传至本课题开发的电机电流信号诊断系统数据库。其中点蚀损伤又分点蚀直径为0.2 mm、0.4 mm和0.7 mm三种，深度均为0.25 mm，分别记为损伤1，损伤2，损伤3。

由于传感器获取的电流信号集成了大量的干扰信息，将影响样本熵计算。故选用sym8小波作为降噪用小波，对信号进行小波分解与重构，从而减少由多次分解带来的端点效应累积误差[6]。

2 样本熵评估复杂性

样本熵(sample entropy，简称SampEn)弥补了近似熵匹配自身数据的缺陷，且精度较近似熵更高[7]。样本熵是用一个非负数来表示时间序列的复杂性，越复杂的时间序列样本熵越大，越规则的时间序列样本熵越小。对轴承损伤定子电流信号信号计算样本熵，其算法如下:

1)信号x(t)中间隔取3 000个数据点，相似容限系数r=0.25SD(c)，SD(c)为x(t)的标准差，取模式维数m=2，重构m维向量:

式中:k=1，2，…M-m

2)计算x(k)与x(n)元素间的距离dkn:

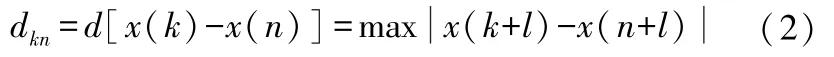
式中:l=0，1….M-m

3)统计每一个dkn小于r的数目以及此数目与距离总数M-m-1的比值Bk m(r):

4)求Bkm(r)的平均值:

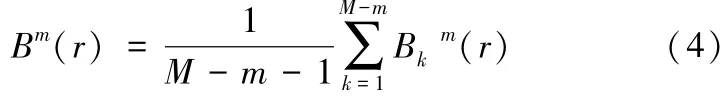
根据维数m，重复1)～4)，得到Bk m+1(r)和Bm+1(r)

5)计算样本熵SampEn(m，r)

通过上述计算得到表1所示结果。

表1 不同损伤时定子电流样本熵

根据表1中数据在不同损伤下，内圈、外圈样本熵熵值明显不一样，相差至少百分位以上，说明对于不同损伤程度的轴承，其电机定子电流信号，样本熵评估复杂性的效果较好。但是同种损伤时内圈、外圈样本熵有时差值仅在千分位，例如图1，图2所示信号波形较为接近，此时内圈、外圈样本熵差值为0.007左右，同样损伤2时差值为0.005左右，而在损伤3时差值又在百分位上。对于前两种情况在误差允许范围内难以区分，甚至可以认为是同一样本熵值。产生的原因是样本熵为单一尺度上时间序列的分析，而轴承定子电流信号是高集成度、非平稳，变化比较微弱的，样本熵不能深层次提取信息来区分信号复杂性。

3 EEMD样本熵评估复杂性

总体平均经验模态分解(EEMD)是在信号中加入白噪声，利用白噪声频率均匀分布的统计特性使信号在不同尺度上具有连续性，促进抗混分解避免模态混叠[8]。对定子电流信号通过以下算法计算EEMD样本熵:

1)在电流信号x(t)中多次加入白噪声ni(t)，其标准差取电流信号标准差的0.4倍，则信号变为xi(t)。

2)对xi(t)进行6层EMD分解，得到满足EMD两个假设条件的分量cij(t)以及余项ri(t)，下标i，j表示第i次加入白噪声分解得到的第j个IMF分量，当分解结束条件时信号可表示为:

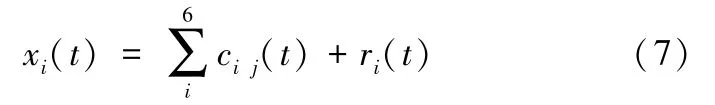
3)对EMD分解后的每一分量进行总体平均运算，计算结果就是EEMD分解后的IMF分量，即:

4)按第2部分样本熵计算步骤1)～5)步计算前4分量的EEMD样本熵。

计算结果是正常、损伤1、损伤2、损伤3各组信号6层分解IMF分量，以及前4分量的EEMD样本熵。由于篇幅有限，给出了部分信号IMF分量，图3是轴承正常时定子电流信号6层EEMD分解后的IMF分量，图4，图5，图6是内圈、外圈、滚动体损伤1时6层EEMD分解后的IMF分量。

图3 轴承正常时定子电流EEMD分解

图4 内圈损伤1时定子电流EEMD分解

图5 外圈损伤1时定子电流EEMD分解

图6 滚动体损伤1时定子电流EEMD分解

可见出现点蚀损伤时信号较复杂，且滚动体定子信号最复杂，内圈次之，外圈最小。内圈、外圈信号的第1，第2，第3分量可以明显看到存在周期性冲击信号特征，第4，第5分量可以看到存在冲击信号特征，但周期性并不明显。此外各个分量包含了不同的时间特征尺度，而轴承损伤引起的故障信息在中高频段，因此第1分量的频率成分最高，第2-6分量的频率成分依次降低。表2-表5为正常和内圈、外圈、滚珠在不同损伤下的定子电流信号EEMD分量样本熵。

表2 正常轴承定子电流EEMD样本熵

表3 损伤1时定子电流EEMD样本熵

表4 损伤2时定子电流EEMD样本熵

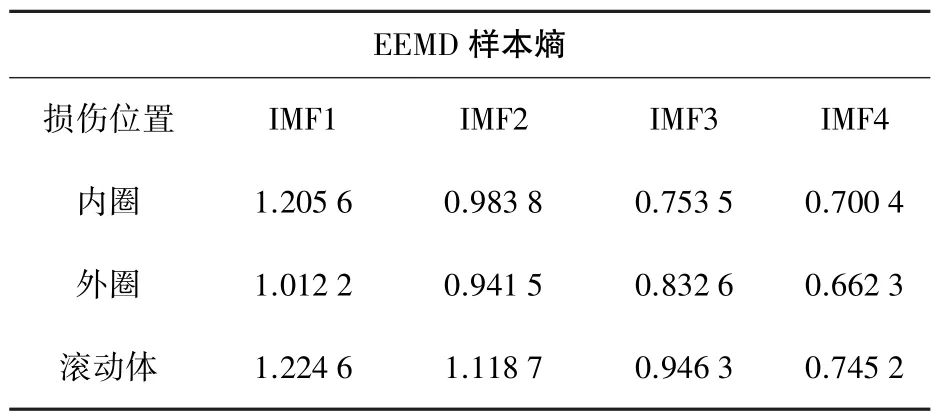
表5 损伤3时定子电流EEMD样本熵

1)表3，表4，表5中可知内圈、外圈在同种损伤时EEMD样本熵相差至少在百分位以上，与表1中同种损伤下内、外圈样本熵值差仅为千分位形成明显对比，表明EEMD多尺度分解弥补了样本熵单尺度分析的缺陷，在评估定子电流信号复杂性时的效果较好。

2)分析表2-5可知定子电流信号各分量EEMD样本熵，损伤轴承明显大于正常轴承，特别是内圈和滚珠的EEMD样本熵更大。表明损伤轴承使得定子电流中产生新模式—电流谐波，并且EEMD样本熵值越大，电流谐波产生的概率越大。

3)正常时的 EEMD样本熵值较小，损伤1时的EEMD样本熵较损伤2的大，较损伤3的小。说明损伤初期轴承各原件冲击较大，定子电流产生较多的电流谐波；损伤中期轴承各元件冲击相对变小，定子电流产生的电流谐波减少；损伤后期轴承各元件冲击又加大，定子电流产生的电流谐波又相应的增多。上述结果表明EEMD样本熵能有效监测和预判电机轴承的运行状态。

4)损伤时定子电流各分量的EEMD样本熵均是IMF1＞IMF2＞IMF3＞IMF4，与 EEMD 分解后的波形变化一致，与越复杂的信号样本熵越大，越规则的信号样本熵越小一致。

5)损伤情况下定子电流任何一个分量的EEMD样本熵滚动体最大、内圈次之、外圈最小。与内圈、外圈、滚动体EEMD分解图2-5的变化趋势一致。

4 结论

文章采用EEMD样本熵来评估电机定子电流信号的复杂性，实例应用和比较结果表明:

1)EEMD能对定子电流信号按时间序列进行多尺度分解，避免了模态混叠的同时有效地弥补了样本熵单一尺度上分析的缺陷，适合于高集成度、非平稳、变化微弱的电流信号。

2)样本熵和EEMD样本熵评估不同损伤下的轴承定子电流信号复杂性时，后者的效果更好，可作为支持向量机等智能故障识别的信号源。

3)轴承从正常到损伤程度逐渐变大的情况下，EEMD样本熵增大-减小-增大的变化趋势准确反映了定子电流的变化趋势，该方法可用于封闭装置中电机轴承运行状态的监测和预测。

[1]Schoen R R，Habetler T G，Kamran F，etal.Motor Bearing Damage Detection Using Stator Current Monitoring[J].IEE Trans on Industrial Applications，1995，31(6):1274-1279.

[2]Blodt M，Granjion P，Raison B，etal.Models for Bearing Damage Detection in Induction Motors Using Stator Current Monitoring[J].IEEE Trans on Industrial Electronics 2008，45(4):1813-1822.

[3]苏文胜，王奉涛，朱泓，等.基于小波包样本熵的滚动轴承故障特征提取[J].振动、测试与诊断，20ll，3l(2):162-166.

[4]胡红英，马孝江.局域波近似熵及其在机械故障诊断中的应用[J].振动与冲击，2006，25(4):38-42.

[5]张超，陈建军.EEMD方法和EMD方法抗模态混叠对比研究[J].振动与冲击，2010，29(s):87-90.

[6]徐仁林，安伟.小波降噪在信号基于EMD的Hilbert变换中的应用[J].噪声与振动控制，2008(6):74-77.

[7]Richman J S，J.Randall Moorman.Physiological time series analysis using approximate entropy and sample entropy[J].Am J Physiol Heart Physio，2000，278:2039-2049.

[8]WU Zhaohua，Huang Norden E.Ensemble empirical mode decomposition:a noise-assisted data analysis method[J].Advances in Adaptive Data Analysis，2009，1(1):1-41.