基于FAST测点的大幅宽HJ星图像几何精纠正方法

李全文， 赵卫林， 杨晓梅， 刘兴权， 张涛

( 1.中南大学地球科学与信息物理学院，长沙 410083； 2.中国科学院地理科学与资源研究所资源与环境信息系统国家重点实验室，北京 100101； 3.郑州市市政勘测设计研究院，郑州 450046)

0 引言

环境与灾害监测预报小卫星星座(HJ-1A /1B星，以下简称HJ星)是我国第一个用于环境与灾害监测预报的专业小卫星星座，也是我国又一个多星多载荷民用对地观测系统，目前在生态环境监测评估、区域环境灾害监测[1]、全球环境影响分析等多方面得到高度重视和广泛应用。刘睿等[2]对HJ图像进行的数据评价表明，整景HJ图像存在较大的整体几何误差，图像在X和Y这2个方向的误差分别超过10和20个像元，且在2个方向的误差没有规律可循，在实际应用中需要考虑几何精纠正问题。

目前，鉴于大幅宽HJ图像整体几何误差复杂的特点，在以HJ图像为数据源、涉及较高精度的分析应用中，多是截取小区域图像，在较少的地面控制点(ground control point，GCP)条件下完成几何精纠正后再进行图像解译。如刘睿等[3-6]都是先对截取的小范围HJ图像数据预处理后再进行分析应用的。一般来说，可依照传统方法选取较少的GCP控制点，采用全局纠正模型完成小范围HJ图像的几何精纠正，使纠正结果满足误差在1～2个像元的精度要求。但如何保证大幅宽HJ图像的工程化应用，将整景图像的无规律几何形变控制在一定精度范围内，快速实现整景HJ图像的几何精纠正，则是个研究新课题。

全局纠正模型中，多项式模型简单易用，一般可以纠正图像的X，Y方向平移、比例尺变形、旋转和倾斜[7]。采用二次多项式模型对平坦地区的IKONOS Geo图像[8]和IRS-1C图像[9]做几何精纠正可得到很好的纠正结果。采用三次多项式模型对 SPOT HRV[10]，TM[11]和IKONOS Geo[12-14]等卫星图像做几何精纠正，在地形起伏较大区域也显示有好的纠正结果。但以上纠正模型只适用于覆盖区域较小、几何变形单一的图像精纠正。有关试验表明，直接将上述全局纠正模型应用于整景HJ星图像，会使纠正后的图像出现某些局部纠正精度比较好、某些局部纠正精度却很差的不均衡情况。因此，对于几何形变复杂的大幅宽图像，应该选择局部纠正模型(如选择基于三角网分割的局部模型)完成图像几何精纠正[15]。基于Delaunay三角分割的“橡皮拉伸”(rubber sheeting)局部纠正模型适用于地面控制点丰富的情况，在控制点足够多的条件下，可以达到很高的纠正精度[15]。然而地面控制点的分布和选取方式也会对图像精纠正的结果造成非常大的影响[16]； 而手动选点方式过于依赖主观经验判断，也不适合进行大量GCP的选取。如采用人工选点方法对HJ图像进行几何精纠正，参照刘盛等[17]得出的精纠正选点密度为0.06～0.09个/km2的结论，1景HJ图像大概需要选择3 000个以上GCP，这对于30 m空间分辨率的HJ图像而言，在肉眼信息识别和精度控制上是不具有可行性的。因此，快速获取大量可靠的GCP及采用局部纠正模型是提高HJ图像几何精纠正精度的关键[18]。

在大幅宽图像的角点检测方法中，从运行效率和精度上考虑，加速分段测试特征(features from accelerated segment test，FAST)算法比尺度不变特征变换(scale-invariant feature transform，SIFT)和最小核值相似区(smallest univalue segment assimilating nucleus，SUSAN)算法更适合于HJ星大幅宽图像获取大量的备选GCP。针对当前算法获取的大量备选GCP仍存在误点以及用于误点筛查的传统均方根误差(root-mean-square error，RMSE)阈值选取过于主观的问题，本文在不依赖数字高程模型(digital elevation model，DEM)和有理多项式参数 (rational poly-nomial coefficients，RPC)[19]条件下，使用相关分析方法分析评估全体候选GCP的质量，并完成误点筛查和获取可靠的GCP； 最后使用基于Delaunay三角分割的“橡皮拉伸”局部纠正模型对HJ图像完成几何精纠正。另外，本文还建立了一套适合于大幅宽图像几何纠正质量评估的多指标精度评价体系，用于评价纠正方法的可靠性和可行性。

1 基于FAST选点的局部几何精纠正

1.1 FAST自动测点与筛查

1.1.1 算法原理

|I(c′)-I(c)|≤t,

(1)

式中：I(c′)为以3像元为半径的圆形窗口中的点的灰度值；t为阈值。只要满足式(1)的连续弧长的数目≥9，则该中心点为角点。实际上，I(c′)到I(c)的距离可以不是1，也就是I(c)的“周围”可以定义为变化的圆或者根据待纠正图像的特点将圆半径设置大一些，那么当I(c′)到I(c)的距离增大时，圆周线上的所有点不一定能满足式(1)的条件； 因此实际纠正时，需要设定一个角点的响应值。对于一个候选点是否为角点，可以通过定义一个角点响应函数(corner response function，CRF)来判断，即

N=∑x∀[c(p)]|I(x)-I(p)|>εd，

(2)

式中：I(x)为圆周线上任意一点的图像灰度值；I(p)为中心像元点的图像灰度值；p为中心像元点即候选点；εd为给定的一个极小阈值。通过上述的角点响应函数，可以累加出圆周上满足式(1)的像元点的个数N。如果N大于给定的阈值，就可以确定该候选点为角点。本文初始阈值取17，用此阈值可以较快地排除部分伪角点。可以通过对比结果选择合适的阈值。完成角点检测后，即可使用HJ星二级数据已有的初始坐标进行关联匹配。

1.1.2 误点筛查

使用FAST算法匹配选点能够生成大量的GCP(可达7 000多个)，其中仍可能存在误差较大的点。在几何变形性质较为单一的情况下，通常根据某个纠正模型的RMSE的大小来判断GCP是否为误点，对于小范围内的图像纠正，该方法能满足误点筛查要求。使用FAST算法获取的大量地面GCP，也可以使用RMSE阈值作为误点的参考。实验发现，通过RMSE阈值选取的GCP只是潜在误点； 在这些潜在的误点中，有时较大的RMSE对应的GCP匹配度可能很高，而较小的RMSE对应的GCP匹配度可能更低。因此，设置合适的RMSE阈值筛查误点并反馈FAST匹配选点是保证HJ图像几何纠正质量的重要环节。

FAST算法在自动匹配进行迭代选点时也进行了初步的伪点筛查，筛查方法基于候选点和邻域点的差值的统计阈值进行，因此伪点检测结果受阈值设置影响较大，同时也受图像质量影响。而现有软件的初次误点检测方法是在获取原始GCP后，当被检验的点和其他大多数点的精度不能很好吻合时，该检验点将被视为误点被剔除[20]； 但所得到的GCP仍包含不满足要求的误点(特别是对大幅宽、几何变形较大图像的处理更是如此)，因此在获取GCP后仍需要进行误点筛查的后处理工作。对误点的筛查往往依赖于个人主观判断，缺乏整体的数据规律分析。以具有代表性的ERDAS软件的误点筛查而言，在获取GCP后，使用全局模型反算GCP的RMSE，通常会主观地把大于某个RMSE值的点作为误点剔除； 由于该方法对RMSE的计算结果偏优[21]，导致误点剔除的阈值筛选具有很大的不确定性，从而使图像几何纠正精度偏低。采用局部模型进行纠正时，ERDAS软件没有提供误点评价的方法，故需要借助全局模型进行辅助性判断。对此，为降低RMSE阈值选择的主观性，本文引入误点和潜在误点的相关性分析方法，从数据的整体规律上确定误点筛查的方法，以此确定合适的RMSE阈值筛查误点，提高GCP的准确性。在阈值范围内，实际误点占潜在误点的百分比最大，在保证GCP数量足够多且分布均匀的情况下，可以将该RMSE阈值对应的GCP删除，或者手动修改误差较大的GCP。

顾客满意是指顾客在接受企业提供的服务或者商品之后的消费感知。顾客的满意受到多方位的影响，包括产品的外观、质量、价格以及销售人员的服务态度等等。顾客的愉悦感越高，满意度就越高。简而言之，就是说顾客满意就是指在消费的过程中感觉良好，能够满足其消费的需求与期望，进而将其自身的感受通过直接表达或暗示的方式对外传递，肯定其消费过程的一种方式。而满意度是消费者根据消费体验做出的感知评价。顾客满意是由多方面的因素产生的，不仅包括企业产品与服务方面，还包括消费者的自身标准。因此要实现顾客满意是一项复杂的工程。

1.2 Delaunay三角网分割

匹配选好同名点并剔除伪点后，即可进行几何纠正。鉴于HJ图像具有较大的整体几何误差，本文采用了Delaunay局部纠正方法。在图像几何纠正中，通过Delaunay原则构建控制点(GCP)三角网，三角网中每个三角形由3个GCP作为三角形顶点。构建好三角网后，使用多项式建立原始图像和目标图像之间的数学转换关系。由于这样的数学转换是通过每个三角形的3个GCP独立运算完成，而不是使用同一个转换模型对整景图像进行转换，因此这种局部模型可以很好地对复杂图像进行分割纠正，获得良好的纠正结果[22]。该方法适合在能够获取大量可靠控制点的条件下使用。

Delaunay的特点是，任意一个三角形外接圆都不包括该三角形之外的顶点(图1)。这使得Delaunay三角网中的每个三角形的内角尽可能接近等角，从而具有很好的局部适应性。

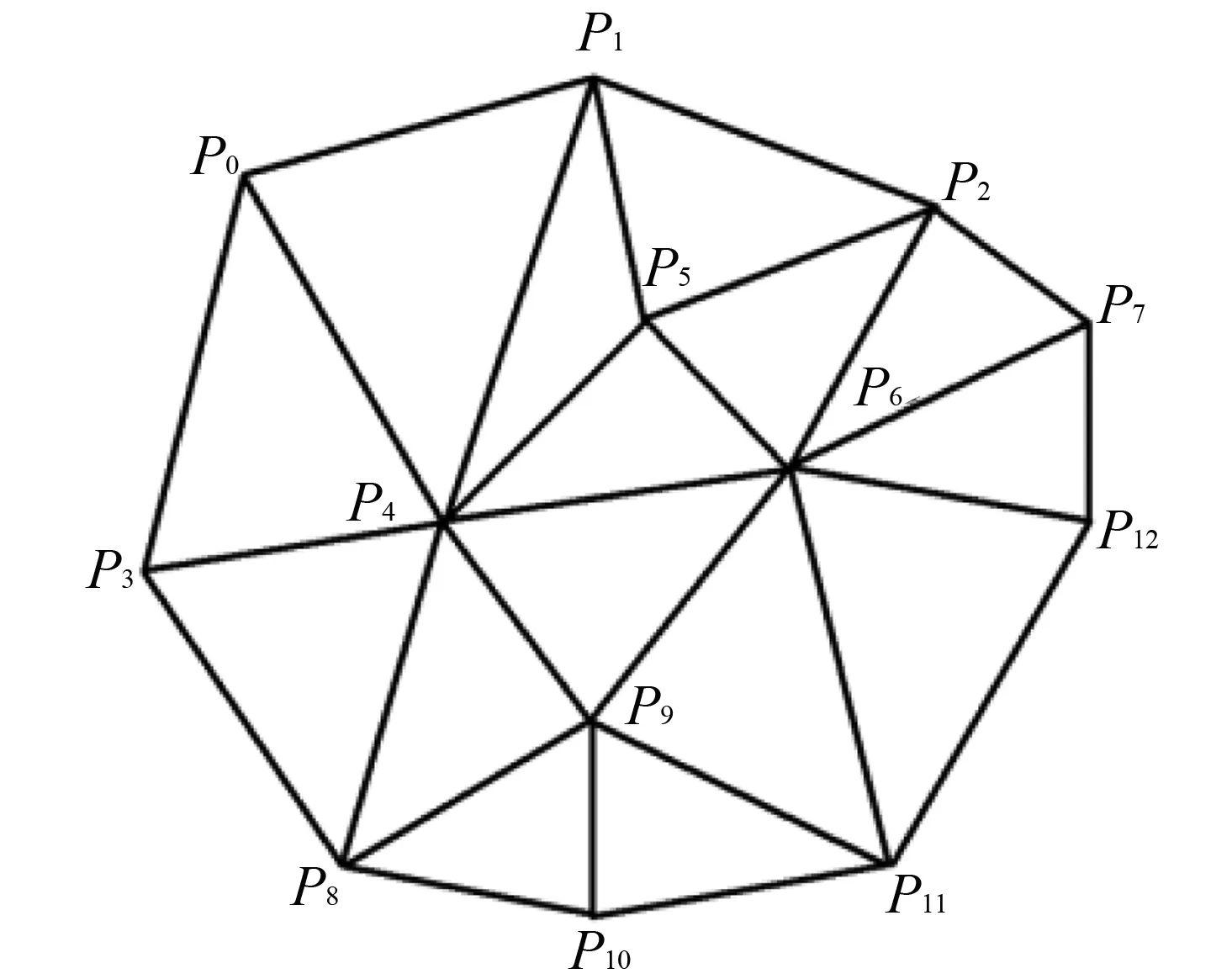
图1 由13个点构成的Delaunay三角网

最为简单和常用的三角形内部纠正模型是一次多项式模型，即

(3)

该模型不需要额外的参数，由3个已知顶点条件即可求解式(3)中3个未知参数，完成转换计算。由于采用“线性橡皮拉伸”(linear rubber sheeting)不一定能得到平滑的纠正结果，因此根据需要还可以使用非线性转换模型。

基于FAST算法计算得到大量的GCP，用GCP构建Delaunay三角网，将整景HJ图像划分为相对较小的区域； 可以认为每一个三角形所覆盖的区域地形相对单一，内部几何形变也相对简单[23]，故使用一次多项式校正模型对每个三角形进行纠正转换。因此，本文采用“线性橡皮拉伸”局部模型对HJ星图像进行几何精纠正。

2 精纠正评价指标

在几何精纠正后图像的误差评估中，小范围图像的几何误差相对简单，一般使用总RMSE和中误差评价图像纠正的优劣。对于大幅宽、几何误差较大的HJ图像的纠正结果，单凭误差统计难以表征图像的误差分布情况和局部误差特性，不足以说明纠正后图像内部各区域误差的大小和分布都满足要求。因此，本文在相关研究[22-25]基础上，建立了HJ图像精纠正的精度评价指标体系，从整体和局部2个方面评价HJ图像的几何纠正精度。评价方法包括： 误差统计、RMSE的空间插值、残差的标准偏差椭圆和残差的空间自相关指数(Moran指数)。

误差统计内容包括基于FAST测算得到的GCP、检核后的GCP、总体中误差、总RMSE和控制点密度。统计方法是从整体给出HJ图像几何精纠正结果的定量描述，获取实验结果的总体特征。

对RMSE进行空间插值则可以直观地掌握HJ图像几何纠正的误差大小和分布范围，以弥补统计法对局部误差评估的不足。获取GCP后，采集了95个独立检核点，以HJ星整景图像作为插值范围，以检核点的RMSE为插值属性，使用反距离加权(inverse distance weighting，IDW)和Kriking方法[26]对HJ图像进行插值评估。

误差统计从总体上给出对图像几何纠正定量误差的描述； 插值能较直观地揭示误差分布范围，但得不到误差偏向的定量描述。使用标准偏差椭圆(standard deviation ellipse)则能度量检核点的RMSE在空间中的方向特征和离散水平[25]； 如果校正后图像的RMSE值很小且分布均一，RMSE的标准偏差椭圆的形状就会接近标准圆，椭圆的偏转方向应该很小[27]。另外，本文使用Moran指数[28]对几何纠正后HJ图像检核点的RMSE的邻近相关性进行评估，判断纠正模型对HJ图像进行几何精纠正的适合程度。Moran指数取值范围为[-1，1](取0值表示不相关，-1表示强负相关，1表示强正相关)。几何纠正精度很高图像的RMSE的分布应该是彼此独立、随机分布的，对应的Moran指数应该趋向于0，检验P值置信度应该很低。

3 实验与结果分析

3.1 实验图像

HJ星分为A星和B星。A，B星分别携载2台设计原理完全相同的CCD相机，双CCD相机具有相同的几何一致性。单颗卫星的单个CCD成像幅宽为360 km，双CCD成像幅宽为710 km[29]。本文实验是基于福建全省HJ图像数据的工程处理进行的，实验涉及A，B星数据。刘睿等[2]结合TM数据对HJ星的A，B星进行的评估表明，A，B星的1A图像具有较大的不规则几何误差。本文使用云覆盖较少的HJ_20111124_454_84_HJ1A-CCD2和HJ_20111224_454_84_HJ1B-CCD2(即A，B星图像)(图2)进行几何误差验证。

图2 HJ A(上)和B(下)星图像相对TM图像的误差

HJ星A，B星图像相对TM图像分别有高达701 m和811 m的异向绝对误差，二者相对TM图像的误差都较大。以编号HJ_20111124_454_84_HJ1B-CCD2的图像做实验说明，HJ图像的覆盖范围如图3所示。

在中尺度应用中，可直接应用TM图像进行土地利用现状和动态变化研究[30]。TM图像的可见光波段和近红外波段的空间分辨率与HJ图像的一致，因此以TM图像作为纠正的基准图像。TM图像幅宽为185 km，远小于HJ图像的710 km，因此，需要使用多景TM图像拼接出覆盖HJ图像的基准图像。如图3所示，基准图像用9景TM图像镶嵌而成(黄色方框内为1景HJ图像的覆盖范围)。

图3 实验区域HJ图像相对TM图像覆盖范围

3.2 精度检核数据

橡皮拉伸模型的控制点残差和RMSE与其他常用纠正模型有所不同。在橡皮拉伸模型中，通过图像匹配得到的所有GCP点都用于Delaunay三角网的构建，三角网上的3个顶点被认为是精确的，即X和Y残差及RMSE都是0。所以，用橡皮拉伸模型进行误差评估时，不能直接用原始GCP的X和Y残差及RMSE； 需要选择不用于构建Delaunay三角网的同名检核点，用于纠正结果的误差评价。实验中，在HJ图像和TM参考图像中分别选取95个同名点作为检核点(图4)。

图4 HJ图像纠正检核点分布

3.3 纠正步骤

几何纠正的步骤可以分为： 基于FAST选取候选点； 使用多项式和相关系数评估候选点精度，并筛除误点； 使用线性橡皮拉伸局部纠正模型进行纠正，并进行精度分析。纠正的关键步骤如图5所示。

图5 基于FAST算法的HJ图像纠正关键步骤

实验中FAST选点可以用Matlab实现，也可以参考现有软件完成，将得到的点导出作为候选点。

3.3.1 FAST选点参数配置

基于FAST算法的测点要求待匹配的2景图像之间有足够的重叠度。本文镶嵌的TM基准图像对HJ图像的重叠度达到100%。此外，FAST测点参数的设置很关键，直接会影响到GCP选点的数量和质量。实验中，将初始的FAST选点阈值设置为20； 由于HJ星图像过大，故将匹配点的搜索增长步长设置为40，迭代次数设置为2。鉴于多个波段之间的匹配运算过于复杂耗时，本文只对HJ图像和TM 图像中的1个波段进行匹配，取匹配效果最好的第3波段作为算法的匹配波段，匹配起始位置为1，最小匹配精度设为0.85，共得到4 635个候选GCP。GCP分布情况如图6所示。

图6 图像匹配测算得到的GCP分布

3.3.2 误点筛查

经图像匹配得到的K个GCP中仍存在不满足匹配条件的误点。本文采用相关分析方法分析RMSE和多项式测算的误点数量与真实误点数量的关系，据此评价所得候选点的整体质量，并根据评价结果修正FAST测点匹配参数。本文在现有软件的误点筛查原理[20]基础上进行改进，采用三次多项式的RMSE阈值筛查误点。以0.1为步长，将RMSE阈值从大到小依次降低，统计每个阈值下的潜在误点数M和实际的误点数N。将统计结果以阈值RMSE为自变量、M和N为因变量，绘制出趋势图(图7)。

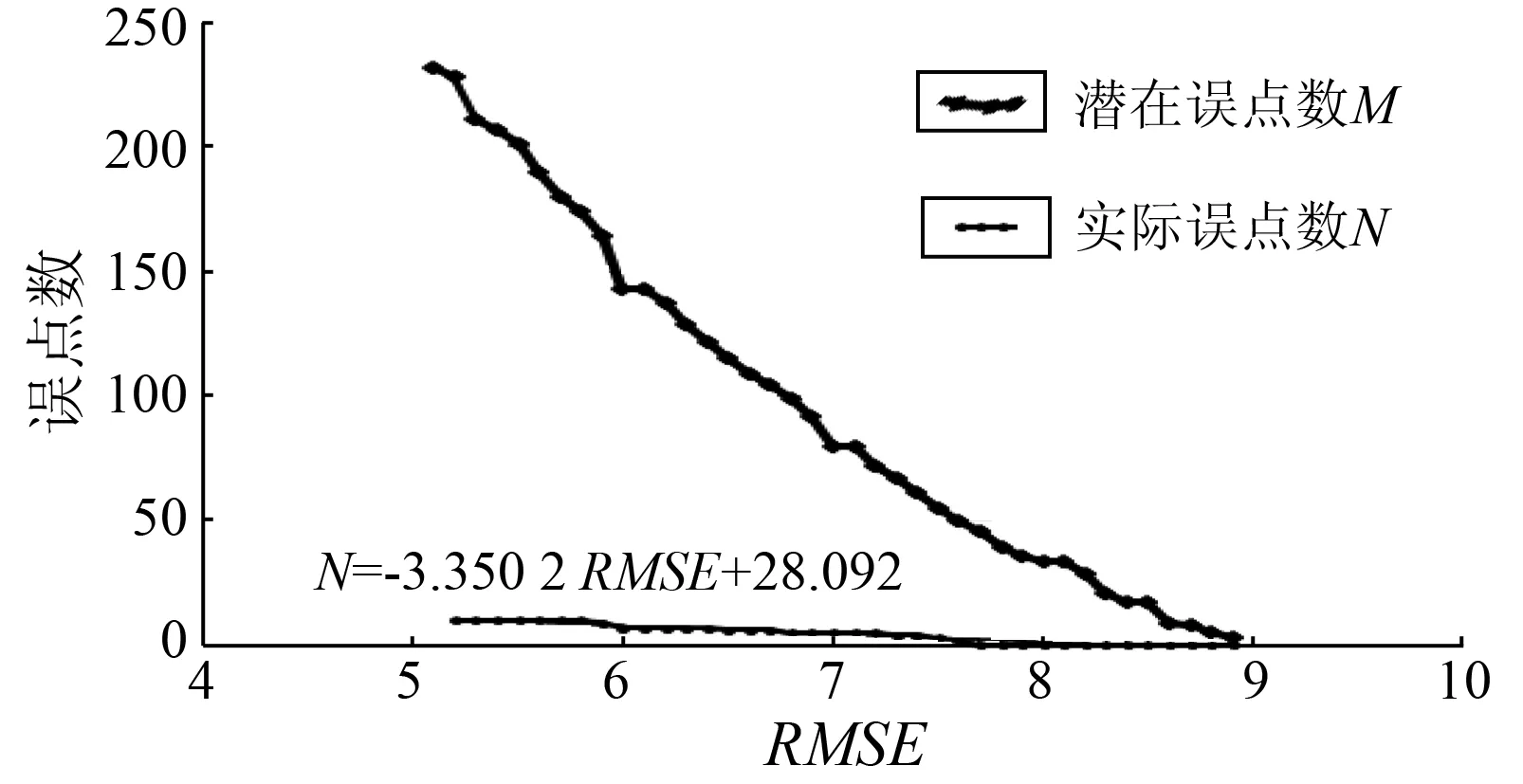
图7 RMSE与潜在误点数M和实际误点数N关系图

计算RMSE阈值和误点数N的相关系数结果如表1所示。RMSE和N的相关系数为-0.097 2，二者呈负相关关系，双尾检验的概率值为0(小于0.01，说明在0.01的置信水平下RMSE和N是显著相关的)。

① 在0.01的置信水平下RMSE和N是显著相关的(双尾检验)。

从图7可以看出，RMSE的阈值从最大的8.9～7.7得到的潜在误点对应的实际误点的数量都是0，这说明大的RMSE阈值不一定能找到匹配不好的GCP。RMSE阈值从7.7～6.4变化范围内，实际误点数量和潜在误点数量呈线性增加，表明在该阈值区间随着RMSE阈值的降低，潜在误点M和实际误点N都在线性增加。在5.9～5.2的RMSE区间内，M增加得很快，而N基本保持不变。在极限条件下，取RMSE为0，得到的实际误点是28个，对应的潜在误点数为4 635个，但实际没有必要在4 635个点中去寻找可能的28个误点。因此，可以取RMSE=5.8作为确定FAST误点的阈值。实验中，找到11个误点，删除1误点，手动更正10误点，总共得到4 634个用于几何纠正的GCP。以上分析说明，如果仅以RMSE在8.9～7.7这个变化范围内找不到误点而认为几何纠正后图像中没有误点，就会造成GCP的误用。以RMSE=5.8作为选择误点的阈值较为适宜，经过检核后的GCP可以保证足够的匹配精度。

根据图7获得的线性方程推算，在极限条件下，RMSE阈值取0时，得到的真实误点数为28个； 对于K=4 635个候选点而言，误点率为0.626%(足够低)，因此原始的算法匹配参数是可取的，所得到的候选点经过修正后可以用于几何纠正。

3.4 精度评价

3.4.1 纠正误差统计及其插值分布

对95个检核点分别计算X和Y方向上的残差、RMSE和GCP密度，得到的结果如表2所示。

从表2可以看出，检核点的总RMSE在1.4个像元以内，表明总体纠正精度非常高。但表2还无法说明图像纠正结果的局部RMSE也能满足要求，因此需要进一步对比分析图8得到的检核点RMSE的Kriking和反距离加权(IDW)插值结果。

图8(a)是Kriking插值结果，色调越接近白色，纠正误差RMSE就越大，其值为0.49～1.48个像元(HJ图像的像元大小为30 m)。该结果已经很好地满足了精度要求。从误差的空间差异分布看，较大的RMSE分布于图像的边缘区域和中间的山地区域，其大小在可接受范围内。对比图8(b)的IDW插值结果，浅灰色环及其内部区域的RMSE≥1.5个像元，最亮区域及其第一环状区域为2个像元≤RMSE≤3个像元。IDW高亮区域在整景图像中仅占很少一部分，说明使用IDW插值和Kriking插值的结果大部分一致，纠正的误差分布均匀平缓，初步说明HJ图像精纠正结果良好。

(a)RMSE的Kriking插值 (b)RMSE的IDW插值

图8 检核点RMSE的插值结果

3.4.2 误差的方向性和随机性检验

对检核点的X和Y方向残差计算标准偏差椭圆，结果如图9所示。所得椭圆很接近于标准圆形，说明检核点残差在各方向呈同质性分布。比照图中比例尺，椭圆的长、短半轴都在1.5个像元以内。将X和Y残差叠置在标准偏差椭圆上可以看出，大部分检核点落在标准椭圆范围内，表明HJ图像纠正结果的精度非常高。

图9 检核点残差的标准偏差椭圆及X和Y残差分布

结合RMSE在HJ图像范围内的空间插值结果可以看出，偏差椭圆表现出的X和Y残差分布的均一性与图8(b)表现出的平坦插值结果非常吻合，说明HJ图像几何精纠正的误差分布满足应用需求，误差大小也在可接受范围内。

使用Moran指数分析检核点的RMSE在空间分布上的相关性，结果如表3所示；RMSE的散点图如图10(a)所示；RMSE的空间联系局部指标(local indicators of spatial association，LISA)显著性分布如图10(b)所示。

表3 检核点RMSE的Moran指数和显著性检验

①以P=0.05做显著性对比值； ②表示Moran指数的期望值。

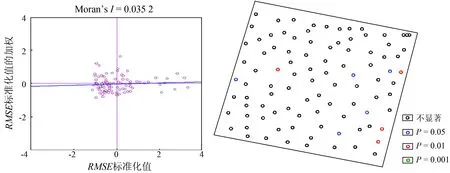
(a) Moran指数散点图(b) 空间联系局部指标显著水平

从地学统计角度而言，如果HJ图像经过几何精纠正后，纠正误差很小、精度很高的话，那么检核点的RMSE在空间上的分布应该是随机的、彼此独立的。表3中的Moran指数为0.035 2，很接近于0值，说明检核点的RMSE的空间关联性非常弱。以0.05做显著性对比值，全局Moran指数的P值为0.23，局部的P值为0.29，2个P值都明显大于0.05，说明RMSE的空间相关性显著水平非常低，即RMSE的空间分布呈不相关的独立分布。在RMSE的显著性分布图(图10(b))的检核点中，绝大多数是黑色和蓝色的点，分别对应不显著或显著水平非常低的状态。全局和局部的P值检验结果都表明几何精纠正的结果误差分布均匀、可信度非常高。

以上对比结果同时说明，本文的RMSE阈值选取方法能反映GCP误点的潜在规律，提高GCP的客观代表性。局部的Delaunay三角分割方法能很好地将具有复杂、无规律几何误差的HJ图像转变为内部相对简单的三角形，纠正后HJ图像的X和Y方向的残差和总RMSE都很小，图像内部没有出现误差突变和局部误差很大的现象，图像总体纠正误差非常小，纠正结果满足应用要求。

4 结论

大幅宽HJ图像存在较大的无规律整体几何误差，采用传统手动采点方式无法满足对HJ图像进行几何精纠正的精度需求。本文提出在使用加速分段测试特征(FAST)匹配算法获取大量GCP、并采用较为客观的RMSE阈值选取方法筛查GCP的基础上，使用“线性橡皮拉伸”局部模型对HJ图像进行几何精纠正，经过残差散点图、残差空间插值、标准偏差椭圆以及Moran指数等方法的检验，得到以下结论：

1)基于FAST匹配测点的局部精纠正方法能获取足够的GCP用于大幅宽HJ图像的几何精纠正。

2)采用“线性橡皮拉伸”局部模型能克服HJ星大幅宽图像的整体几何变形复杂的问题。

3)使用本文方法对大幅宽HJ图像进行精纠正后的误差很小、分布均匀、独立性强，能确保图像精纠正后的精度满足在1.5个像元以内的要求。

4)本文算法实现简单，在需要使用到整景HJ图像几何精纠正的情况下，使用本文局部模型纠正方法能够缩短精纠正的时间，降低进行图像精纠正的工作强度，减少主观操作误差，确保图像质量。

参考文献(References)：

[1] 邓钟,池天河,张新,等.基于HJ星的灾害特征信息自动反演系统[J].计算机工程,2012,38(11):231-233.

Deng Z,Chi T H,Zhang X,et al.Disaster characteristics information automatic inversion system based on HJ satellite[J].Computer Engineering,2012,38(11):231-233.

[2] 刘睿,孙九林,王卷乐,等.环境与灾害监测预报小卫星CCD数据质量评价[J].地球科学进展,2011,26(9):971-979.

Liu R,Sun J L,Wang J L,et al.Data quality evaluation of Chinese HJ CCD sensor[J].Advances in Earth Sciences,2011,26(9):971-979.

[3] 刘睿,孙九林,张金区,等.中国北方草地覆被的HJ星NDVI校正研究[J].草业学报,2011,20(1):189-198.

Liu R,Sun J L,Zhang J Q,et al.HJ NDVI cross-calibration for grassland in Northern China[J].Acta Prataculturae Sinica,2011,20(1):189-198.

[4] 李花,李卫国,黄义德.利用HJ星遥感进行水稻抽穗期长势分级监测研究[J].遥感信息,2010,12(6):55-58.

Li H,Li W G,Huang Y D.The monitoring rice growth condition in heading stage by HJ-A/B satellite images[J].Remote Sensing Information,2010,12(6):55-58.

[5] 王琼,王克如,李少昆,等.HJ卫星数据在棉花种植面积提取中的应用研究[J].棉花学报,2012,24(6):503-510.

Wang Q,Wang K R,Li S K,et al.Cotton planting area extraction based on multi-temporal HJ remote sensing[J].Cotton Science,2012,24(6):503-510.

[6] Yang F,Juanle W,Pengfei C,et al.Comparison of HJ-1A CCD and TM data and for estimating grass LAI and fresh biomass[J].Journal of Remote Sensing,2012,16(5):1000-1008,1012-1023.

[7] 钟小明.林区高空间分辨率遥感影像几何精校正算法研究[D].西安:西安科技大学,2011.

Zhong X M.Research on geometric rectification of high resolution remote sensing image in forest area[D].Xi’an:Xi’an University of Science and Technology,2011.

[8] Hanley H B,Fraser C S.Geopositioning accuracy of IKONOS imagery:Indications from two dimensional transformations[J].The Photogrammetric Record,2001,17(98):317-329.

[9] Zoej M J V,Mansourian A,Mojaradi B,et al.2D geometric correction of IKONOS imagery using genetic algorithm[J].International Archives of Photogrammetry and Remote Sensing and Spatial Information Sciences,2002,34(B4):1-6.

[10]Okamoto A,Fraser C,Hattorl S,et al.An alternative approach to the triangulation of SPOT imagery[J].International Archives of Photogrammetry and Remote Sensing,1998,32(4):457-462.

[11]Pala V,Pons X.Incorporation of relief in polynomial-based geometric corrections[J].Photogrammetric Engineering and Remote Sensing,1995,61(7):935-944.

[12]Ahn C H,Cho S,Jeon J.Ortho-rectification software applicable for IKONOS high resolution images:GeoPixel-Ortho[C]//IEEE 2001 International Geoscience and Remote Sensing Symposium.Sydney,NSW:IEEE,2001:555-557.

[13]Fraser C,Hanley H,Yamakawa T.Three-dimensional geopositioning accuracy of IKONOS imagery[J].The Photogrammetric Record,2002,17(99):465-479.

[14]Vassilopoulou S,Hurni L,Dietrich V,et al.Orthophoto generation using IKONOS imagery and high-resolution DEM:A case study on volcanic hazard monitoring of Nisyros Island(Greece)[J].Isprs Journal of Photogrammetry and Remote Sensing,2002,57(1/2):24-38.

[15]蔡喜琴,曹建君,蔡迪花,等.中巴地球资源卫星CCD影像几何纠正方法比较[J].遥感技术与应用,2006,21(4):396-398.

Cai X Q,Cao J J,Cai D H,et al.Compare and analysis of CBERS CCD image geometric rectification algorithms[J].Remote Sensing Technology and Application,2006,21(4):396-398.

[16]Wang J H,Ge Y,Heuvelink G B M,et al.Effect of the sampling design of ground control points on the geometric correction of remotely sensed imagery[J].International Journal of Applied Earth Observation and Geoinformation,2012,18:91-100.

[17]刘盛,刘庆忠,李国伟.基于RS和DGPS的SPOT5图像几何精校正研究[J].安徽农业科学,2009,37(25):12335-12337.

Liu S,Liu Q Z,Li G W.Study on geometric precision correction of SPOT5 images based on RS and DGPS[J].Journal of Amhui Agricultral Sciences,2009,37(25):12335-12337.

[18]Ma L X,Zhou T Y,Xü J.Remote sensing image geometric accurate rectification based on automatic matching and triangulation[J].Journal of Remote Sensing,2011,15(5):927-939.

[19]刘江,岳庆兴,邱振戈.RPC校正方法研究[J].国土资源遥感,2013,25(1):61-65.

Liu J,Yue Q X,Qiu Z G.Research on the approach to RPC emendation[J].Remote Sensing for Land and Resources,2013,25(1):61-65.

[20]Leica.Leica Geosystems Geospatial Imaging[M].IMAGINE AutoSyncTMUser’s Guide,2007.

[21]Brovelli M A,Crespi M,Fratarcangeli F,et al.Accuracy assessment of high resolution satellite imagery orientation by leave-one-out method[J].ISPRS Journal of Photogrammetry and Remote Sensing,2008,63(4):427-440.

[22]Leica.Leica Geosystems Geospatial Imaging[M].ERDAS Field Guide,2010.

[23]王新刚.遥感影像几何校正精度分析[D].北京:中国地质大学(北京),2009.

Wang X G.Geometric correction precision analysis for remote sensing image[D].Beijing:China University of Geosciences(Beijing),2009.

[24]李立钢,刘波,尤红建,等.星载遥感影像几何精校正算法分析比较[J].光子学报,2006,35(7):1028-1034.

Li L G,Liu B,You H J,et al.The comprehensive comparison of several algorithms for precision rectification of satellite imagery[J].Acta Photonica Sinica,2006,35(7):1028-1034.

[25]王江浩,葛咏.遥感影像几何校正的GCP残差模拟分析[J].遥感技术与应用,2011,26(2):226-232.

Wang J H,Ge Y.Simulation analysis of GCP residuals in the remote sensing image registration[J].Remote Sensing Technology and Application,2011,26(2):226-232.

[26]杨成生,张勤,张双成,等.改进的Kriging算法用于GPS水汽插值研究[J].国土资源遥感,2013,25(1):39-43.

Yang C S,Zhang Q,Zhang S C,et al.Research on GPS water vapor interpolation by improved Kriging algorithm[J].Remote Sensing for Land and Resources,2013,25(1):39-43.

[27]Mitchell A.ESRI GIS the ESRI Guide to GIS Analysis:Spatial Measurements and Statistics vol.2.[M].California:ESRI Press,2005.

[28]王劲峰,廖一兰,刘鑫.空间数据分析教程[M].北京:科学出版社,2010.

Wang J F,Liao Y L,Liu X.Spatial Data Analysis Turtorial[M].Beijing:Science Press,2010.

[29]李传荣,贾媛媛,胡坚,等.HJ-1光学卫星遥感应用前景分析[J].国土资源遥感,2008,20(3):45-46.

Li C R,Jia Y Y,Hu J,et al.An analysis of the prospects of HJ-1 optical satellites in remote sensing application[J].Remote Sensin for Land and Resources,2008,20(3):45-46.

[30]冉有华,李文君,陈贤章.TM图像土地利用分类精度验证与评估——以定西县为例[J].遥感技术应用,2003,18(2):81-86.

Ran Y H,Li W J,Chen X Z.Verification and assessment of land use classification by using TM image:Taking Dingxi County as an example[J].Remote Sensing Technology and Application,2003,18(2):81-86.