基于模糊贴近度和改进Prim算法的高光谱图像波段分组排序
2014-09-13张转马玉蔡伟
张转, 马玉, 蔡伟
(西北工业大学电子信息学院,西安 710072)
0 引言
高光谱成像技术通过飞行平台搭载的不同成像光谱仪,在电磁波谱的紫外、可见光、近红外和中红外区域,以数十到数百个连续且细分的光谱波段对目标区域同时成像,在获得地表图像信息的同时,也获得其光谱信息,将地物的光谱特征与图像相结合,提供了大量丰富的信息。高光谱图像的数据量巨大且极其宝贵,所以在高光谱图像压缩领域中,无损压缩[1-2]成为研究热点,其中预测算法以其简单且优良的性能被广泛应用。
虽然高光谱图像波段间的相关性较强,但是由于大气、水吸收等原因,使得高光谱图像中一些波段与相邻波段的相关性下降,若直接采用波段的自然顺序进行预测编码,则很难获得理想的压缩效果。波段的分组排序是波段预处理算法中的一个重要部分,它可以使波段间相关性较强的图像作为一组进行预测编码; 一般情况下,排序后的编码效率可比没有排序的编码效率提高1%~5%[3]。针对波段排序,目前应用最为广泛的是基于图论生成树的普里姆(Prim)算法。一个连通图的生成树是一个极小连通子图,它含有图中全部顶点,但只有足以构成一棵树的(n-1)条边。Prim算法的基本思路是在无向加权图中根据权重寻找最优生成树来选取最优路径。由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点,且其所有边的权值之和亦为最小。若从图的某顶点出发,可以系统地访问到图中所有顶点,则遍历全图时经过的边和图的所有顶点所构成的子图,称作该图的“生成树”。文献[4]最早将Prim算法用于高光谱波段排序中,以2个波段间压缩后的数据大小作为Prim算法的权重,但此算法需要预先计算波段间的编码代价,复杂度较高。Fernhdez[5]基于信息论理论,采用波段间的互信息作为Prim算法的生成树的权重; 但由于互信息计算比较复杂,实际中采用相关系数来代替互信息,算法复杂度比文献[4]有较明显降低。目前最常见的方法是采用相关系数作为Prim算法的权重[6-7]。相关系数与互信息相比,计算相对简单。但是在一些硬件设备的计算及存储能力有限的情况下,进行星载高光谱图像压缩,传统的基于相关系数加权的Prim算法仍过于复杂,因此需要开发更为简单快速的波段分组排序算法。
本文在传统的Prim算法基础上,研究简化其权重参数的计算和满秩邻接矩阵的稀疏化; 引入模糊贴近度中的最大最小贴近度(maximum and minimum closeness,MMC)[8]衡量波段间相关性,根据MMC将全波段分成相关性高与相关性低的2个子集。在进行波段排序时,通过计算MMC得出Prim算法的满秩邻接矩阵,结合高光谱图像的特点将满秩邻接矩阵简化为稀疏邻接矩阵,选取有效波段参与比较,避免了全波段的比较。通过上述方法,大大降低了高光谱图像分组排序的复杂度。
1 Prim波段排序算法
高光谱图像波段间的相关性一般采用相关系数来衡量。对于高光谱图像的波段排序,传统的算法选择相关系数作为Prim算法的权重。相关系数ρ[9]是衡量2个随机变量之间线性相关程度的指标,其定义为
(1)
式中:ρB-1,B为第(B-1)波段与第B波段的相关系数;fB(x,y)为当前波段的当前像素值;fB-1(x,y)为前一波段的相同位置的像素值;uB-1为前一波段的像素平均值;uB为当前波段的像素平均值;M,N分别为图像的行数、列数,单波段图像的空间大小为M像素×N像素。
在基于相关系数权重的Prim波段排序算法中,每个波段对应一个节点,2个波段连线形成边,2个波段的相关系数作为该边的权值,高光谱图像谱间的相关性关系表示成一幅无向加权图(图1)。图1中①,②,③和④为节点(即波段);数字为2个节点间的相关系数(即权重)。
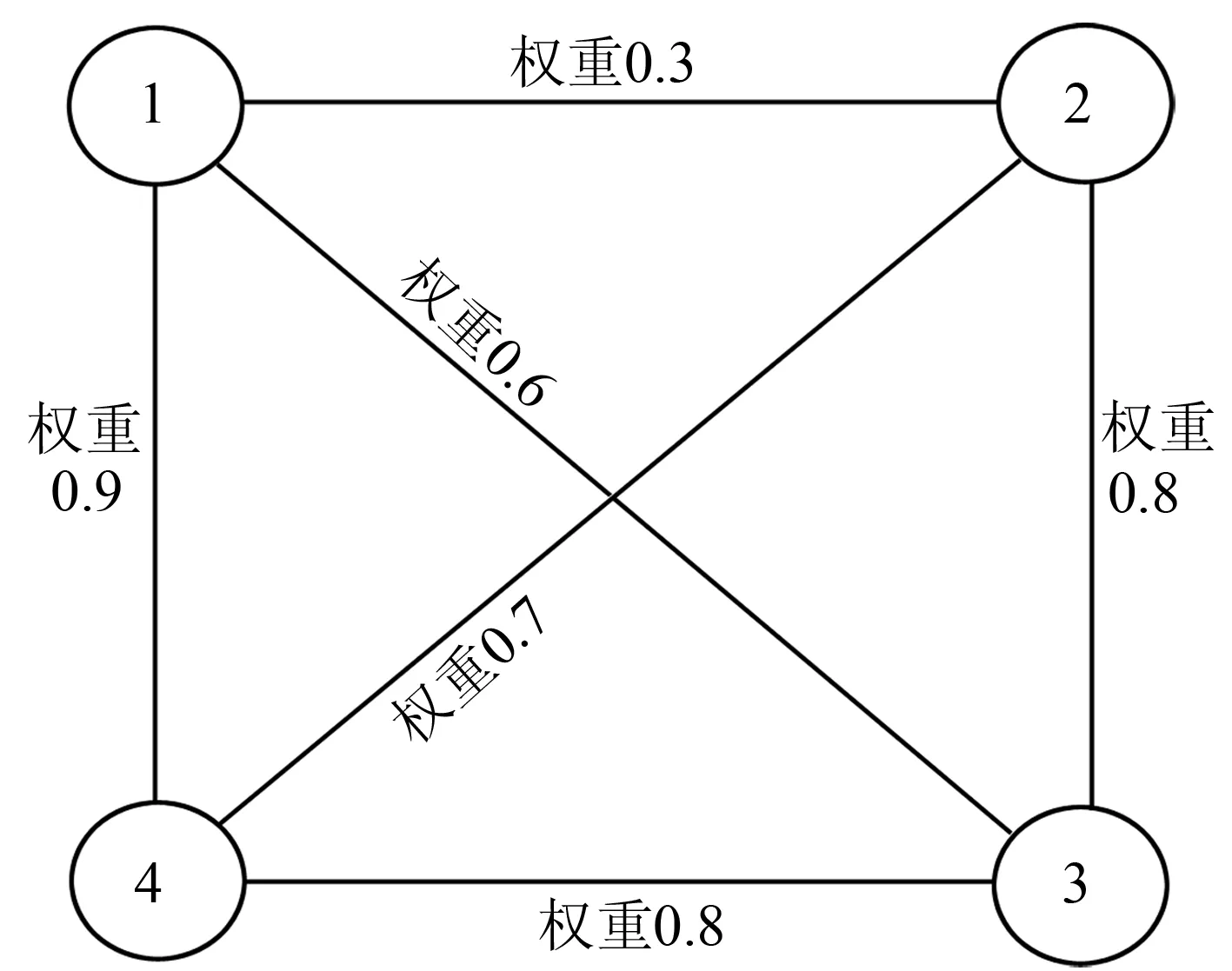
图1 无向加权图
最优生成树的定义是从一个节点数为n的无向加权图中选择(n-1)条边,使得图中所有节点都被连接,同时各边权重累加值最小或最大。因而,最优波段排序问题就转换为在加权图中寻找一棵各边权值之和为最高的生成树的问题。
Prim算法[10]一般通过邻接矩阵表述各个节点的权重。图1的邻接矩阵如表1所示。

表1 邻接矩阵
基于相关系数的Prim算法,高光谱图像的波段排序过程如下: ①设图像的波段总数为K,T和S分别代表最优生成树已包含波段和剩余波段的集合,即分别对应已预测的波段和未预测的波段; 首先对集合T和S进行初始化,令T集合为空集合,即T={Ø},S={1,2,…,K}; ②选取任意一个波段为初始波段v0,将v0加入集合T,此时T={v0}; ③搜索满足u∈T,v∈S-T的最大相关系数hu,v,可得波段u为波段v的参考波段; 同时将波段v从集合S移入集合T中; ④重复步骤③,直到S={Ø}。
按照上述步骤执行Prim算法,取图1中节点①为初始顶点,生成的最优生成树如图2所示。
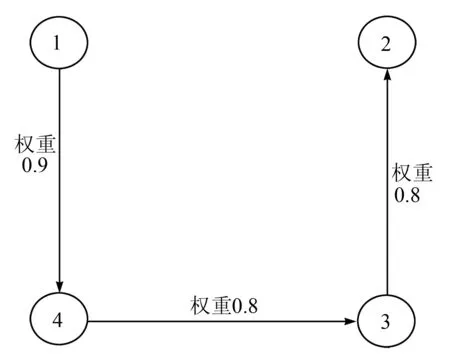
图2 最优生成树
编码时,对生成树初始波段采用波段内编码,其余波段依次按照生成的最优波段顺序编码; 当前波段通过与之相连的前一波段进行波段间预测,完成整景高光谱图像数据的压缩编码。
2 快速波段分组排序
采用相关系数作为Prim算法的权重参数,复杂度很高; 且在进行排序时,由于邻接矩阵是满秩的,每个波段都需要其余所有波段参与比较,计算量非常大。针对上述问题,本文提出简化Prim算法的权重参数,并对满秩邻接矩阵进行稀疏化,以降低波段分组排序的复杂度。
2.1 基于MMC的谱间相似性度量
贴近度[11]是对2个模糊集贴近程度的一种度量,在模式识别等实际应用中起着极为重要的作用。通过贴近度来衡量2个集合之间的距离,进而描述出2个集合之间的相似度。贴近度越小,距离越远,2个集合间的相似性越差; 反之,相似性越好。贴近度包括最大最小贴近度(MMC)、最小平均贴近度、海明贴近度和欧几里德贴近度等,其中以MMC最为简单,且性能优良,因而被广泛使用。
高光谱图像是成像光谱仪对同一地物在不同光谱范围中连续波段的成像,能产生一条完整而连续的光谱曲线,具有波段间相关性极强的特性; 同时,相邻波段的同一位置的点相似度极高。利用上述特性,选择各类贴近度算法中计算最为简洁的MMC来衡量2个波段的相似程度,可以有效地简化计算的复杂度。同时,MMC对原始变量的分布与性质没有要求,适合衡量高光谱图像波段间的相关性。
本文将高光谱图像的每个波段看做是一个模糊集,用MMC衡量各个波段间的相关性。由于模糊集内元素的取值范围在区间,而高光谱图像的原始像素是用16 bit表示的,因此基于高光谱图像的MMC[12]可定义为
(2)
式中MMCB-1,B为前一波段(B-1)与当前波段B的MMC。由于式(2)的分子和分母均包含常数因子2-16,则式(2)可简化为
(3)
图3是选取的高光谱图像OMIS-I河场景的波段间相关系数与MMC曲线图。
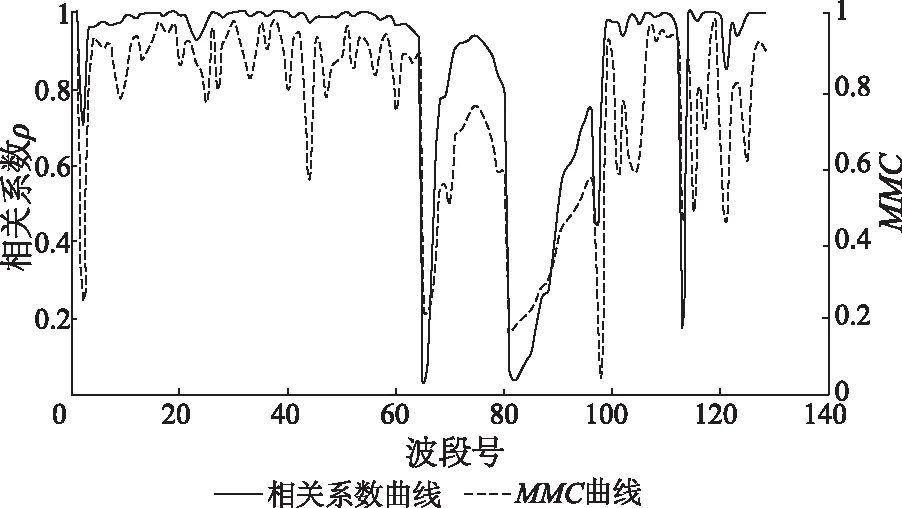
图3 河场景的波段间相关性
从图3可以看出,MMC和相关系数ρ所反映的波段间相关性基本一致。因此,MMC测度也可以反映波段间相关性的强弱,但其计算复杂度会大大降低。
本文使用式(3)的MMCB-1,B衡量高光谱图像波段间的相关性。设单波段图像的空间大小为M像素×N像素,表2比较了计算2个波段间的相关系数ρ和MMC的复杂度。

表2 相关系数ρ与MMC运算次数比较
从表2可以看出,计算MMC的复杂度大约是计算相关系数复杂度的一半,通过使用MMC代替相关系数,可明显减少运算量。
2.2 邻接矩阵的稀疏化改进
传统的Prim算法不断选取集合T与集合S-T中2点连成的最大权值的边,因此其邻接矩阵是满秩的,全部波段均参与比较,计算复杂度高。因波段间的相关性存在很大差异,在实际中并不需要对所有波段都进行比较。本文算法将Prim算法的满秩邻接矩阵简化为稀疏矩阵,对每个满秩邻接矩阵仅提取有效波段(即每个满秩邻接矩阵中与其相关性较高的那些波段); 这是因为Prim算法进行大量比较,就是为了寻找与每个满秩邻接矩阵中相关性较强的波段。但大部分波段与当前波段相关性不强,对这些波段进行比较没有意义,所以只需对有效波段进行比较,从而大大减少比较次数。
高光谱图像波段间的相关性较强,但随着波段数的增多,距离越远的波段间相关性变差。一般情况下,当前波段与前后相邻波段的相关性较强,因此可利用高光谱的数据特性对满秩邻接矩阵进行稀疏化。具体操作为: ①计算MMC初步得到的邻接矩阵是满秩的; ②比较当前波段与前一波段和后一波段的MMC,将其中最大的MMC设为MMCmax; ③将当前波段和其他波段的MMC与MMCmax进行比较,如果MMC>MMCmax,则确定为有效波段,保留MMC; 否则赋值为0。通过上述方法选出每个满秩邻接矩阵中的有效波段,对有效波段进行比较,可以明显降低排序的复杂度。
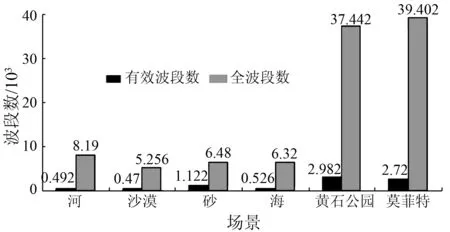
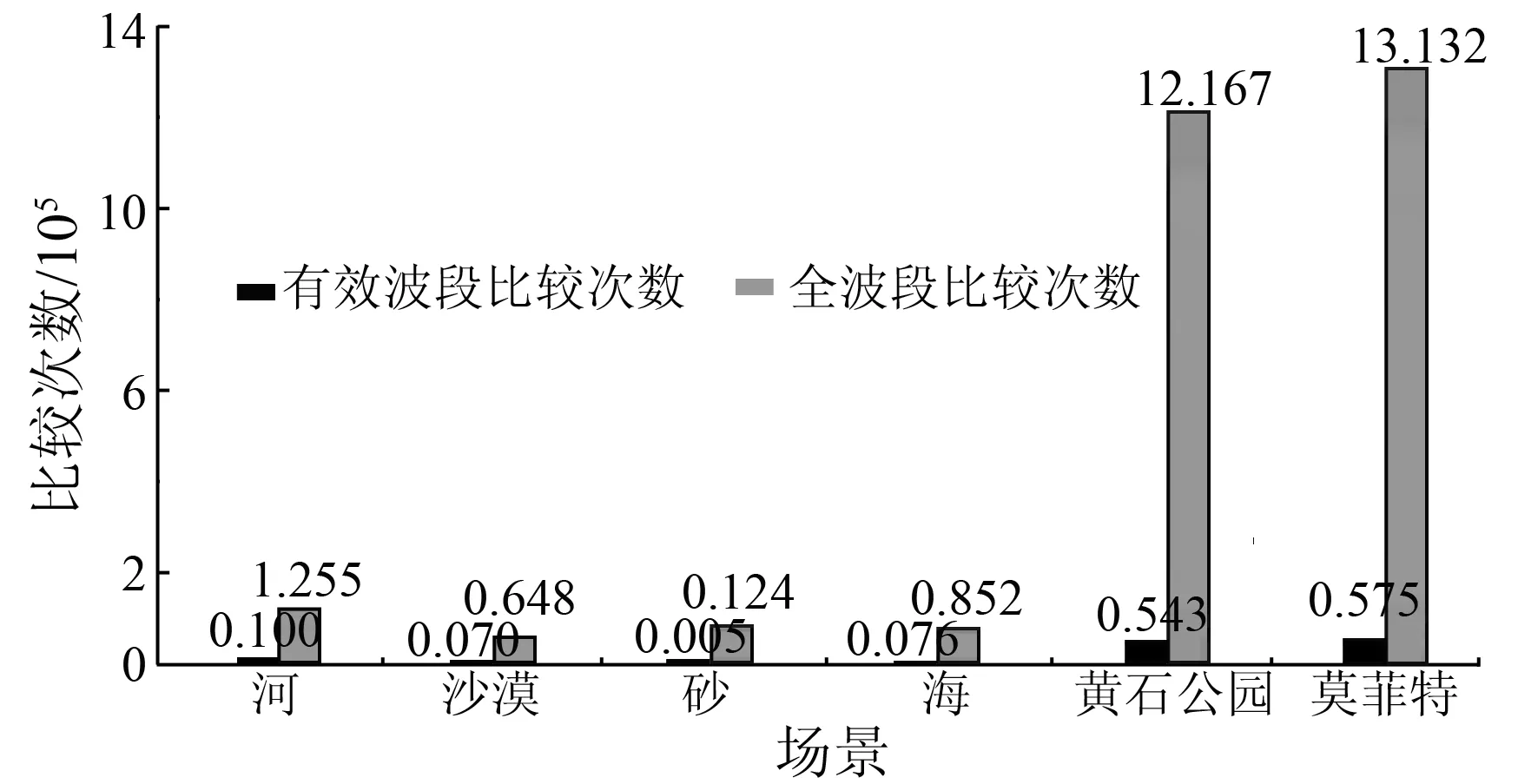
下面简要分析Prim算法[13]中使用满秩邻接矩阵比较所有波段与使用稀疏邻接矩阵比较有效波段的比较次数。设节点总数为m,依次按照最优生成树的集合,定义为集合R,依据其包含的节点数来分析全波段排序的比较次数。设集合R包含l个节点(0 (4) 稀疏邻接矩阵有效波段的比较次数为Eb,即 Eb=m(m-2)+P, (5) 式中:m(m-2)为选取有效波段的比较次数;P为有效波段通过Prim算法的比较次数。比较次数的多少与所保留的有效波段的位置和数量有关,而不同高光谱图像数据的有效波段的位置和数量也不尽相同。数据统计表明,有效波段总数占全波段总数的大约6%~17%。可见,采用稀疏化的邻接矩阵,比较次数明显降低。 鉴于上述情况,本文提出基于MMC的改进Prim算法进行高光谱图像波段排序,并进行进一步编码,算法流程如图4所示。 图4 基于改进Prim波段分组排序的高光谱图像压缩算法框架 本文采用全波段分组排序的算法,首先去除全零的噪声波段; 然后采用本文提出的MMC作为高光谱数据的谱间相关性参数,通过MMC实现波段分组,将波段分成相关性高与相关性低2组。具体操作为计算每个波段与其他波段的MMC并比较、求出每个波段的最大MMC,定义为MMCmax; 比较MMCmax与阈值Th,若MMCmax>Th,则进行邻接矩阵稀疏化,进而基于Prim算法进行波段排序,然后对排序后的波段进行3D-calic[14]的空谱结合的谱间预测算法,最后进行JPEG2000无损压缩; 若MMCmax 实验选取我国自行研究的实用型模块化成像光谱仪(object modulariaztion imaging spectrometer,OMIS)中的OMIS-I[15]获取的河、沙漠、砂和海4个场景的原始高光谱图像数据和1997年由美国宇航局喷气动力实验室开发的机载可见光-近红外成像光谱仪(airborne visible infra-red imaging spectrometer,AVIRIS)获取的黄石公园(Yellowstone)和莫菲特(Moffet)2个场景(http: //compression.jpl.nasa.gov/)的高光谱数据,其中OMIS-I遥感数据由国家“863”信息获取与处理主题提供。AVIRIS数据由224波段组成,光谱范围覆盖可见光谱到近红外区(400~2 500 nm); OMIS-I数据的波长范围为0.46~12.5 μm,波段数为128。2种类型数据的图像大小均为512像素×512像素,每个像素用2个字节16 bit表示。实验平台为奔腾双核处理器,CPU主频为2.60 GHz,内存为1.96 GB,工作环境为Windows XP系统,编译器为Matlab 2010。 由于数据特性不同,本文依据实验得出OMIS-I和AVIRIS数据波段分组的阈值分别为0.9和0.85; 且由于AVIRIS相邻波段间的相关性比较强,能从每个满秩邻接矩阵选出来的有效波段过少,所以在采用本文满秩邻接矩阵稀疏化操作时,统一将MMCmax降低5%,进行矩阵稀疏化,选出有效波段。 1)比较使用传统的基于相关系数的Prim全波段排序编码算法(称为“算法1”)和本文提出的基于MMC稀疏化邻接矩阵的Prim算法(称为“算法2”)的波段排序运行时间。实验结果见表3和表4。 表3 OMIS-I波段排序运行时间 表4 AVIRIS波段排序运行时间 从表3和表4可以看出,对于OMIS-I和AVIRIS这2种数据,本文提出的算法2的波段排序运行时间普遍较低,与算法1相比,平均波段排序复杂度分别降低了27%和23%。 表5对比了算法1和算法2的压缩效率。 表5 算法1和算法2的压缩效率比 从表5可以看出,本文提出算法2与传统的算法1相比,压缩性能基本保持不变。 2)比较采用Prim算法对满秩邻接矩阵的全波段比较排序和对稀疏化邻接矩阵选取的有效波段比较排序的复杂度。对于传统的满秩邻接矩阵而言,设谱间波段的全波段数为n,每个波段的相关波段数为(n-1),则整个图像的相关波段总数为n(n-1)。本文只讨论波段排序的效率,此时河、沙漠、砂、海、黄石公园和莫菲特6种场景的排序总波段数n分别为91, 73, 81, 80,194和199。采用本文方法对满秩邻接矩阵稀疏化,分别选出6个场景的有效波段; 将每个稀疏邻接矩阵选出来的有效波段数相加,得到这景图像的有效波段总数。有效波段与全波段的波段总数对比结果如图5所示。 从图5中可以看出,河、沙漠和海3种场景数据的有效波段的波段总数都远小于全波段的波段总数,而砂场景由于当前波段与相邻波段的相关性较差,所以选出来的有效波段总数及其占全波段总数的比例相对于其他场景数据要多一些。6组数据的有效波段总数大约占对应全波段总数的6%~17%。 图5 不同场景有效波段与全波段数目比较 针对不同场景数据,通过式(4)(5)分别计算全波段和有效波段的比较次数,结果如图6所示。 图6 不同场景有效波段与全波段比较次数 从图6可以看出,6种场景的有效波段比较次数远小于全波段比较次数,有效波段比较次数大约占对应全波段比较次数 的5%~14%。因此可以认为,简化满秩邻接矩阵为稀疏邻接矩阵的方法是本文算法复杂度降低的关键技术。 1)本文在分析相关系数作为Prim算法权重的基础上,提出用模糊数学的最大最小贴近度(MMC)衡量高光谱图像波段间的相似性,无论是在对高光谱图像进行波段分组,还是在波段排序方面均取得很理想的效果,而且可用于衡量高光谱波段间的相关性。 2)利用高光谱图像波段特性,对Prim算法的满秩邻接矩阵进行稀疏化,提取有效波段进行比较,避免了进行全波段比较。实验证明,与传统的基于相关系数的Prim算法排序相比,本文提出的算法复杂度降低了27%,压缩性能基本持平,且提高了波段预处理的效率。 参考文献(References): [1] 万建伟,粘永健,苏令华,等.实用高光谱遥感图像压缩[M].北京:国防工业出版社,2012. Wan J W,Nian Y J,Su L H,et al.Applied Compression of Hyperspectral Remote Sensing Images[M].Beijing:National and Defense Industry Press,2012. [2] 罗建书,周敏,孙蕾.高光谱遥感图像数据压缩[M].北京:国防工业出版社,2011. Luo J S,Zhou M,Sun L.Data Compression of Hyperspectral Remote Sensing Image[M].Beijing:National and Defense Industry Press,2011. [3] Toivanen P,Kubasova O,Mielikainen J.Correlation-based band-ordering heuristic for lossless compression of hyperspectral sounder data[J].IEEE Geoscience and Remote Sensing Letters,2005,2(1):50-54. [4] Tate S R.Band ordering in lossless compression of multispectral images[J].IEEE Transactions on Computers,1997,46(4):477-483. [5] Fernhdez G.Ubiergo lossless region-based multispectral image compression[J].IPA97,1997,443:15-17. [6] Toivanen P,Kubasova O,Mielikainen J.Correlation-based band-ordering heuristic for lossless compression of hyperspectral sounder data[J].IEEE Geoscience and Remote Sensing Letters,2005,2(1):50-54. [7] Pizzolante R,Carpentieri B.Visualization,band ordering and compression of hyperspectral images[J].Algorithms,2012,5(1):76-97. [8] 刘法贵,赵娟.模糊贴近度及应用[J].华北水利水电学院学报,2006,27(3):104-106. Liu F G,Zhao J.Fuzzy similarity and application[J].Journal of North China Institute of Water Conservancy and Hydropower,2006,27(3):104-106. [9] 钟新联.统计学原理[M].上海:立信会计出版社,2008. Zhon X L.Principles of Statistics[M].Shanghai:Lixin Accounting Press,2008. [10]江波,张黎.基于Prim算法的最小生成树优化研究[J].计算机工程与设计,2009,30(13):3244-3247. Jiang B,Zhang L.Research on minimum spanning tree based on prim algorithm[J].Computer Engineering and Design,2009,30(13):3244-3247. [11]孟广武.区间值Fuzzy集的基本理论[J].应用数学,1993,6(2):212-217. Meng G W.Basic theory for interval-valued Fuzzy sets[J].Mathe-matica Applicata,1993,6(2):212-217. [12]袁宏俊,杨桂元.基于最大-最小贴近度的最优组合预测模型[J].运筹与管理,2010,19(2):116-128. Yuan H J,Yang G Y.The combination forecast model based on the biggest-smallest approach degree[J].Operations Research and Management,2010,19(2):116-128. [13]丁国强,吕治国.基于Prim算法最小生成树优化的研究[J].甘肃联合大学学报:自然科学版,2009,23(5):67-69. Ding G Q,Lü Z G.Optimization algorithm of minimum spanning tree based on Prim[J].Gansu Union University:Natural Science,2009,23(5):67-69. [14]Zhang J,Liu G Z.An efficient reordering prediction-based lossless compression algorithm for hyperspectral images[J].IEEE Geoscience and Remote Sensing Letters,2007,4(2):283-287. [15]刘银年,薛永祺,王建宇,等.实用型模块化成像光谱仪[J].红外与毫米波学报,2002,21(1):9-14. Liu Y N,Xue Y Q,Wang J Y.Operational modular imaging spectrometer[J].Journal of Infrared and Millimeter Waves,2002,21(1):9-14.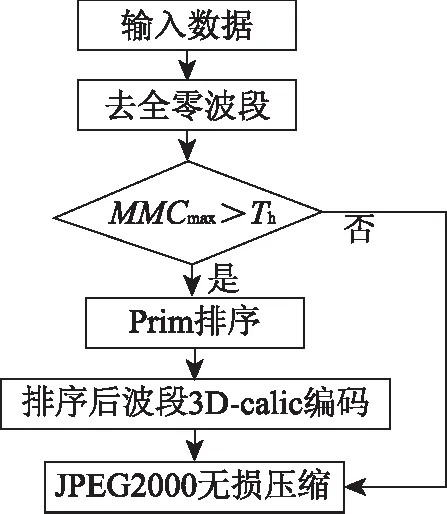
3 实验结果与分析



4 结论
