6-THRT并联机器人的误差模型研究

阮远强，李开明

(南京理工大学机械工程学院，江苏南京210094)

0 前言

19世纪上半叶人们就开始了对并联机构的研究，其中比较著名的是发明了Stewart平台的英国工程师Stewart。1961年美国的Unimation公司生产出了第一台工业机器人后，机器人行业开始了迅猛的发展，进而促使并联机器人成为了人们关注和研究的热点。并联机器人相对于串联机器人而言具有结构稳定、刚度大、承载能力强、多自由度、运动灵活等优点。但是并联机器人的结构相对复杂，致使精度问题成为其能否广泛运用的一个关键因素。目前提高并联机器人精度的主要方法是通过精度设计和运动学标定［1-2］。

1 并联机床机构模型及位姿方程

1.1 并联机床机构模型

本文研究的Stewart平台式的6-THRT型并联机构简图如图1所示。每根杆与上下平台之间用虎克铰相静，静平台上的点b1-b6和动平台上的点m1-m6分别为相应虎克铰的安装点，并且各杆上还装有一个螺旋副可以随机构自由伸缩。各静动平台坐标系分别简称为o系、p系，原点取在各平台的中心点处y0轴垂直于b3b4，z0轴垂直于静平台向上，x0轴的方向按右手定则确定。p坐标系按相同的方法建立。设计一种中心轴测量方法，中心轴的两端安装点分别为上下平台的中点(o、p系的原点)。通过在轴上安装6个传感器来获得相邻运动关节的夹角与位移变化信息，要保证其始终处于不受力状态。

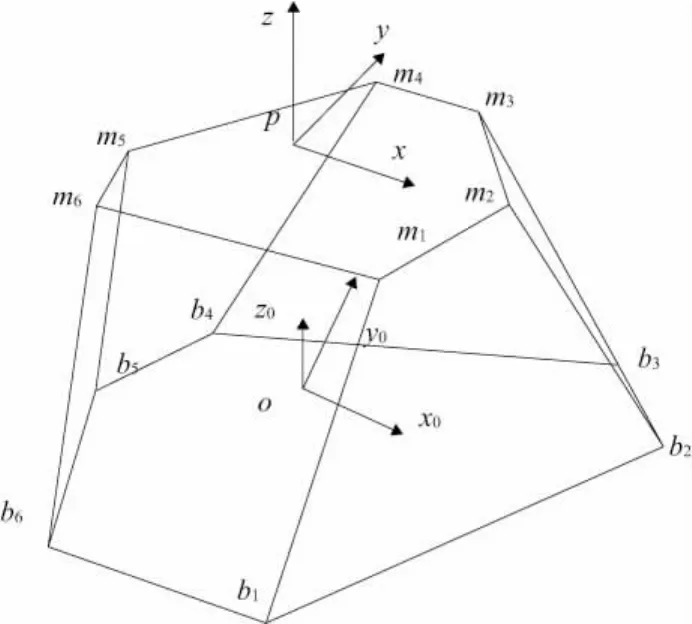
图1 机构结构简图

1.2 机床位姿方程

在中心轴的各运动关节处建立坐标系如图2，建立测量机构的运动学方程，如式(1)所示:

图2 中心轴机构的坐标系简图

其中:(α、β、γ)表示坐标系{t}相对坐标系{s}的姿态矩阵，其中，α，β，γ分别是坐标系{t}相对坐标系{s}的坐标轴x，y，z的三个独立转角。r表示坐标系{t}的原点在坐标系{s}中的位置。参考坐标系{s}原点固联于b3，b4的中点，工具坐标系{t}原点固联于m3，m4的中点。

式(2)为坐标系{s}与参考坐标系{o}之间的固定转换关系，坐标系{s}先绕 zs轴旋转90°，然后绕 xs轴旋转90°，最后沿zs轴方向平移一个位移d0与坐标系{o}相重合。

式(3)为坐标系{6}到工具坐标系{t}的固定转换关系。坐标系{6}绕y6轴旋转90°与坐标{t}相重合。

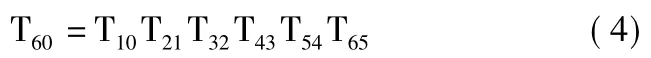
式(4)为中心测量轴的坐标传递关系矩阵。

由中心测量轴坐标系的建立可以得到相邻坐标系间的D-H参数，如表1所示。

表1 中心测量轴的D-H参数

2 机床动平台位姿误差计算模型

2.1 位姿误差建模方法

上述测量机构虽然可以避免间接测量所带来的误差，但是由于测量轴本身存在的加工制造安装误差，以及关节间隙和6个传感器的测量误差，会使得动平台的理论运动轨迹与实际运动轨迹之间存在误差。因此必须对中心轴进行误差建模，找出其主要误差源，然后对其加以补偿以提高测量的准确度和并联机床的精度。

针对本机构的特点，可以将其看成一个串联的单开链机构，采用一般工业机器人的位姿误差分析方法，可知中心测量轴的末端位置和姿态误差，近似表示为:

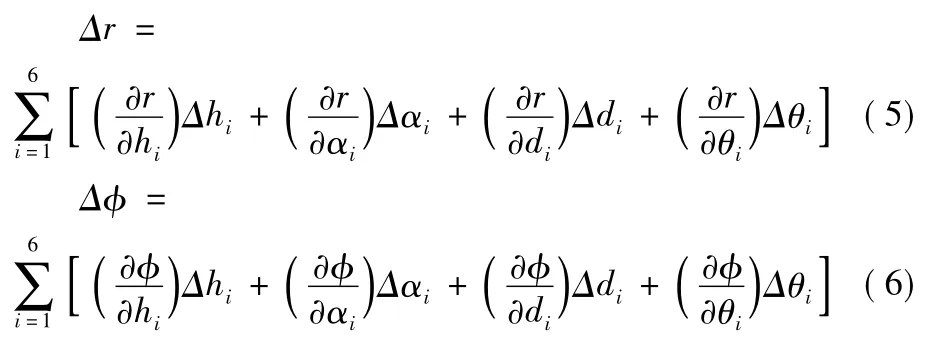
式中，r和Φ分别表示为动平台的位置和姿态向量，hi，αi，di，θi(i=1，2，…，6)为各连杆的运动变量和结构参量。

2.2 末端位姿误差模型

在上面的运动学方程中，其相邻坐标系间的D-H变换矩阵表示为式(7)。

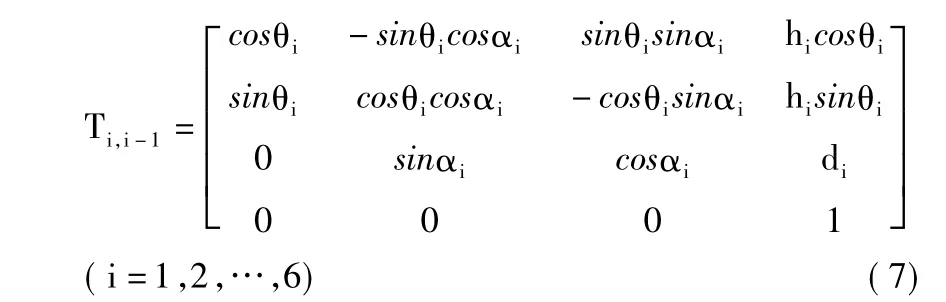
可知位姿误差模型即为位姿矩阵对于 hi，αi，di，θi(i=1，2，…，6)等几何参数的偏导数即:

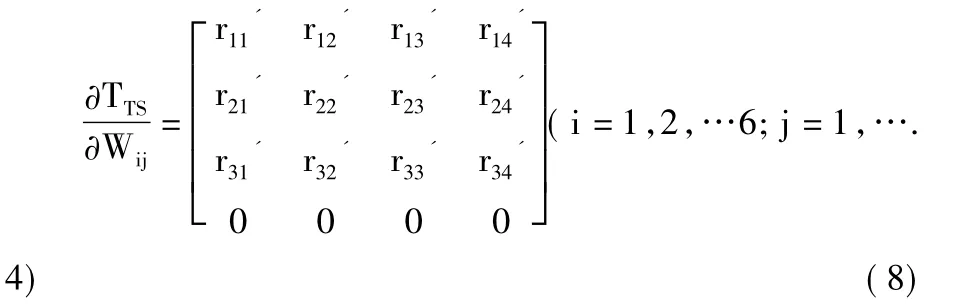
联合式(5)、式(6)可以得到末端位置和姿态向量的相应偏导数方程为:

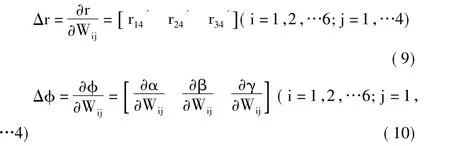
结合式(1)-式(4)和式(7)可以求出矩阵TTS中各个因子的相应几何参数表达式，然后根据(α，β，γ)表示式，可以求得末端位姿的三个位姿角α，β，γ，如式(11)、式(12)、式(13)所示:

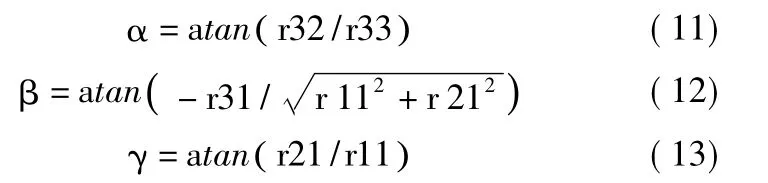
结合式(1)-(4)和式(7)-(13)，求出相应的偏导数方程与位置和姿态的表达式，然后将其带入式(5)、式(6)，即可以求得本机构的末端位姿误差表达式［4-7］。然后通过下面的仿真分析来判断该机构的主要误差因素。

3 仿真分析

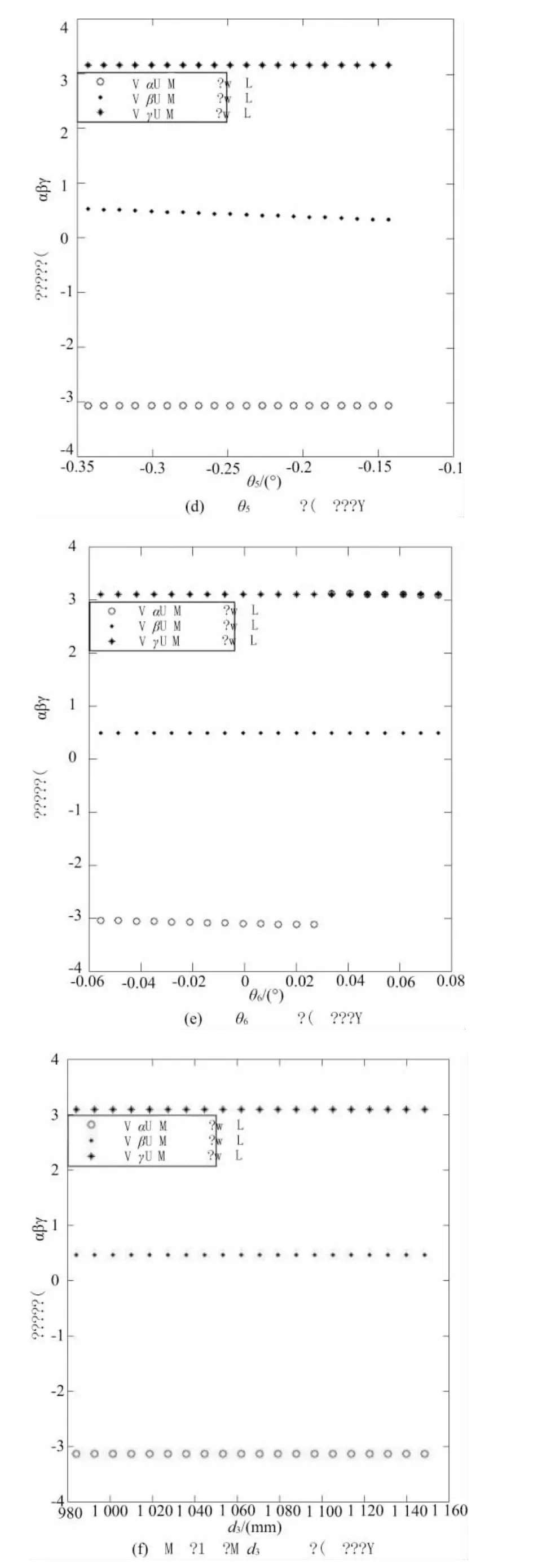
现采用固定单杆杆长法对机构进行20组数据的采集，然后结合Matlab软件编写相关程序，对机构的末端位置误差 Δr(Δx，Δy，Δz)和姿态误差 ΔΦ(α，β，γ)进行仿真和分析，找出其主要误差因素。参见图3，图4，图5，图6。

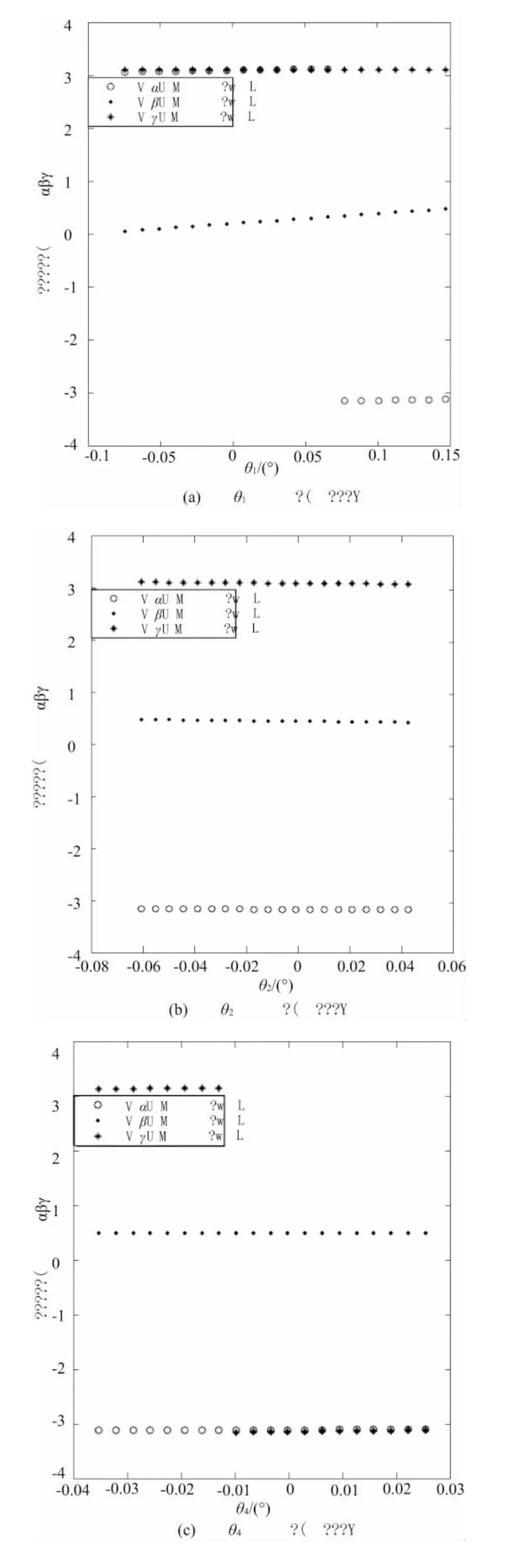
各几何结构参数对动平台位姿α，β，γ方向上的影响

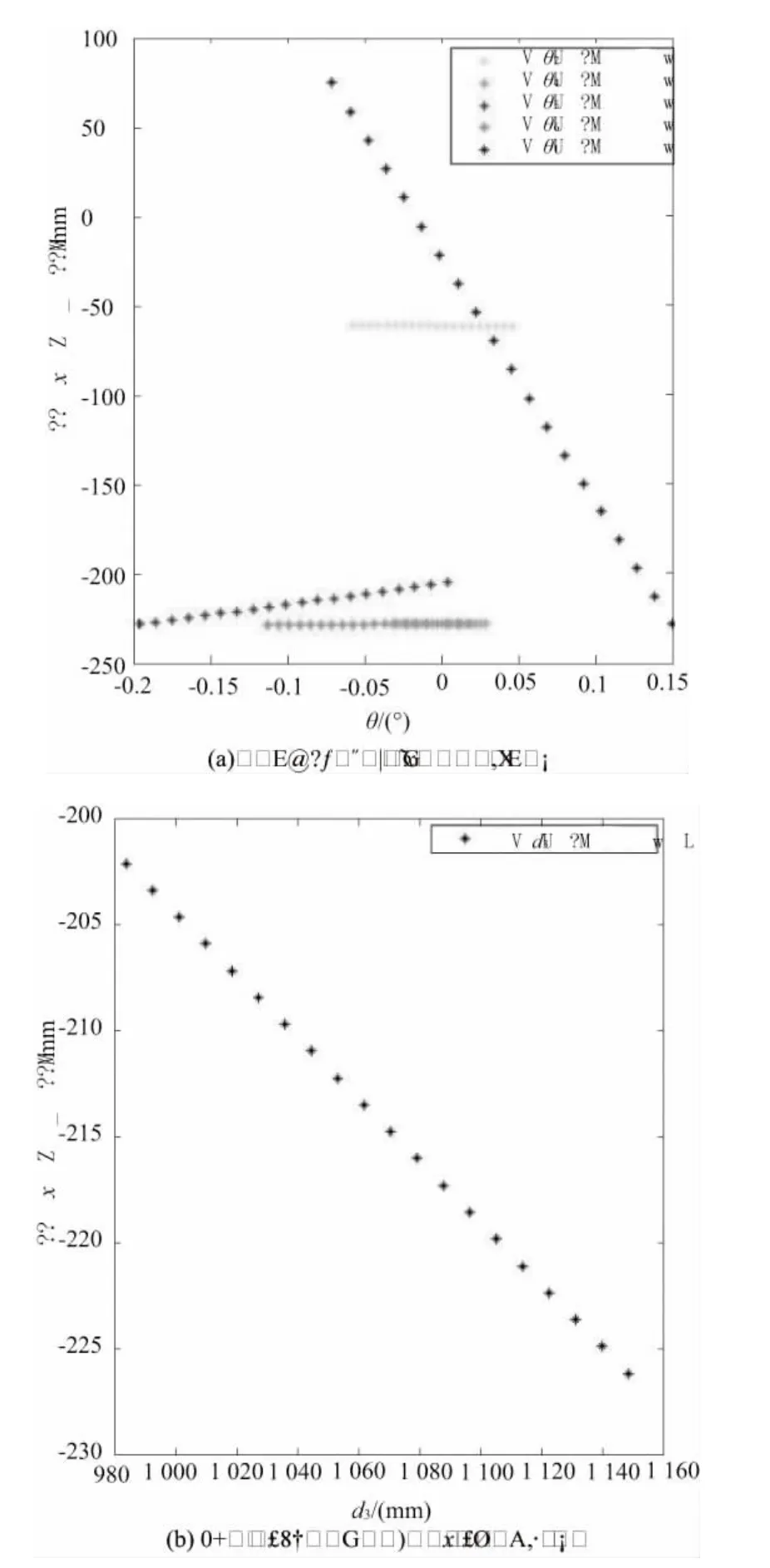
图4 各几何结构参数对动平台x方向上的影响

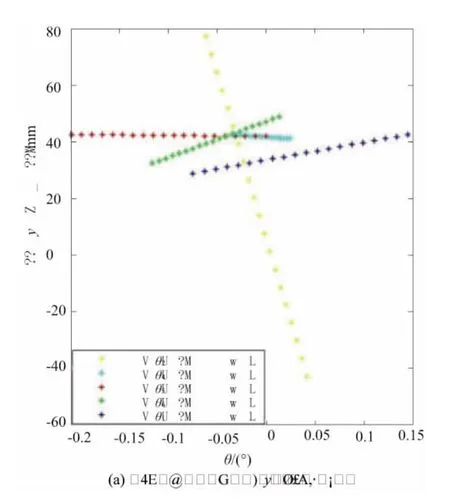
图5 各几何结构参数对动平台y方向上的影响

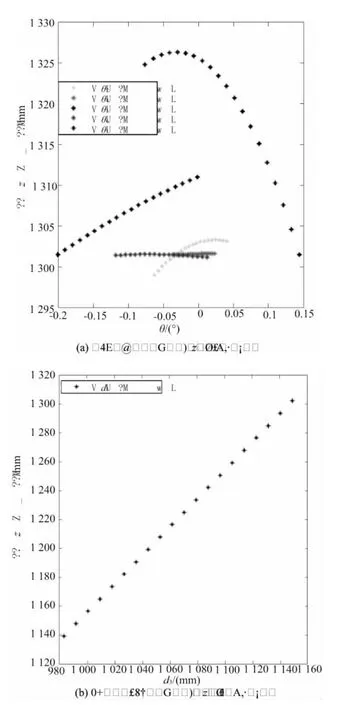
图6 各几何结构参数对动平台z方向上的影响

从上图可以知道在小范围内运动，θ1，θ2对动平台位置变化的影响是比较明显的，证明铰链的制造安装和间隙误差会对机构位置会产生较大的影响。而转角对动平台位姿角的影响不大(除了奇异点位置)，可能是由于本机构的运动范围比较小所导致的。此次仿真结果为机构的误差补偿提供了一定的理论研究依据。

4 结论

针对本文所分析的6-THRT型并联机构，并结合matlab对其进行运算仿真，可以得到如下结论:

1)本文采用了一种中心轴测量模型的直接测量方法，避免了因间接测量而引起的部分误差因素。在安装过程中，测量机构要保证始终处于不受力状况，进一步减少了测量机构的误差源，间接地提高了本测量机构精度。

2)针对本机构的特点，采用了基于D-H矩阵的一般工业机器人误差分析法，该方法将铰座安装位姿误差、铰链制造误差以及测量轴本身和驱动杆长等几何误差全部计入到了误差模型中，通过Matlab分析，铰链的制造与安装是该并联机构末端产生误差的主要因素，因此在设计与安装时要尽量减小机构静态误差，以提高机床的精度。

［1］黄真，孔令富，方跃法.并联机器人机构学理论及控制［M］.北京:机械工业出版社，1997，35(4):1-5.

［2］D.Stewart.”A platform with six degrees of freedom，”Proc.Inst.Mech.Eng.，1965/1966，180(5):371-386.

［3］Wang.S.M.Error Model and Accuracy Analysis of a Six-Dof Stewart platform［C］.Manufacturing Science and Engineering，1995，2(1):519-530.

［4］李叔祥.6-THRT并联机器人的标定研究［D］.南京:南京理工大学，2004.

［5］陆敏智.6-THHT并联机器人的多传感器测控系统研究［D］.南京:南京理工大学，2006.

［6］叶冬明.新型大工作空间并联机构及其性能研究［D］.南京:南京理工大学，2012.

［7］单鹏，谢里阳，田万禄，等.基于D-H矩阵的Stewart型并联机床位误差计算模型［J］.机械工程学报，2010，46(17):186-190.