基于Creo及SimMechanics对3-TPT并联机构的运动学仿真与模拟

2014-09-12刘伟锐赵恒华

机械制造与自动化 2014年4期

刘伟锐，赵恒华

(辽宁石油化工大学机械工程学院，辽宁抚顺113001)

0 引言

并联机构作为一种新型的运动机构，近年来受到学者广泛的研究和探索，其具有刚度质量比大、响应速度快、加工精度高、环境适应性强和技术附加值高等优点［1］。利用计算机仿真软件可以快速准确的模拟出其空间结构和运动规律，它能够在设计时预测机构的性能并进行优化，及时地发现产品不合理甚至错的设计，不但可以缩短设计周期，减少研究经费，而且还可以提高设计品质，降低研制风险。

Matlab是Math Works公司推出的当今国际上最为流行的软件之一。Matlab中的SimMechanics是一个对动态系统进行建模、仿真和分析的软件包，其主要功能是将连杆、关节等机械部件用抽象的模块来表示，只需设置各部分模块的质量惯量特性和坐标系统，就可以得到完整机械系统的模型。在控制系统研究过程中，Simulink是最常用的软件之一，它输入参数简单，能够实时观测图像变化，所以受到广大研究者的青睐。本文利用模糊控制箱和Simu-link建立了模糊PID控制器，并与SimMechanics的模型想连接，构成整体的控制模型，并展开对3-TPT并联机构的探索与研究。

1 机构组成与工作原理

3-TPT并联机构简图如图1所示，其主要结构由定平台、动平台、平行机构、连杆和驱动杆等几部分组成。动平台与定平台均为正三角形，每根驱动杆和平行机构分别用虎克铰与动平台和定平台连接，伺服电机驱动三根驱动杆的伸缩，通过改变各驱动杆的长度，可以调整动平台的位置［2］。三根驱动杆承受外力，由从动平台和支撑杆组成的平行机构限制三个转动自由度，承受外力矩。图1为3-TPT并联机构的Creo虚拟样机模型(说明:由于平行机构对整个模型运动学方程无影响，所以建模时忽略了平行机构)。

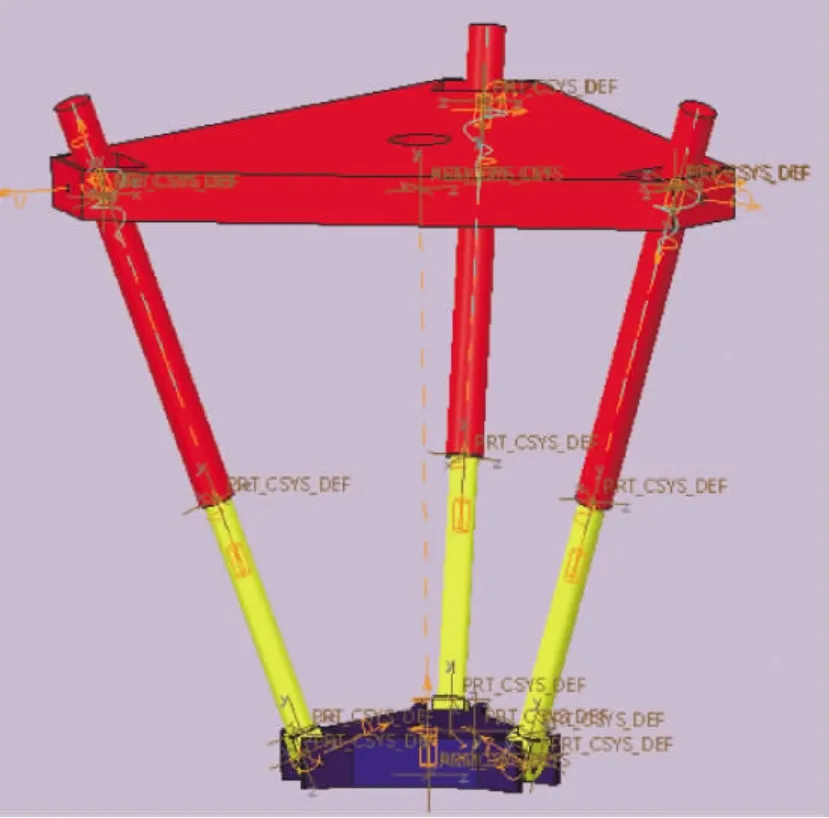
图1 3-TPT并联机构模型

2 运动学方程的建立

机构上下平台铰链中心点均按正三角形布置，各边对应分别平行，两平台相对位置在运动中始终保持平行，没有任何姿态变化。首先，在定平台中心建立基础坐标系oa-xayaza，xa轴正方向与 a1a2相交，ya轴正方向过点 a1，za方向竖直向下；同理，在动平台中心建立动坐标系ob-xbybzb，xb轴正方向与 b1b2相交，yb轴正方向过点 b1，zb方向竖直向下，如图2 所示［3］。

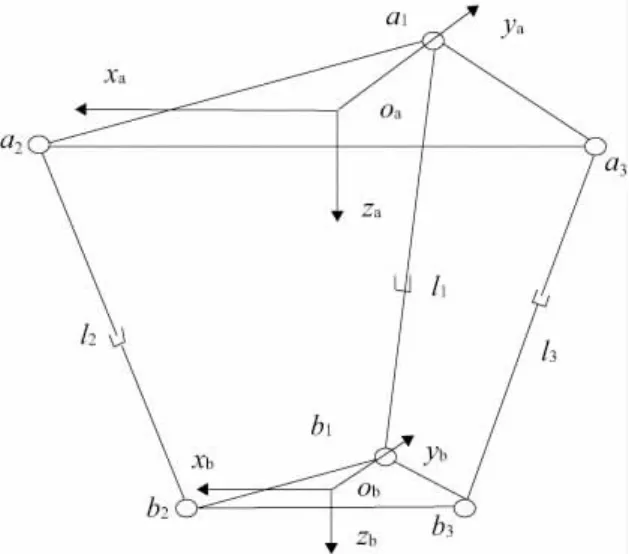
图2 3-TPT并联机构的空间坐标系

设定平台外接圆半径为R，动平台外接圆半径为r，并使 R ＞r；各驱动杆 a1b1，a2b2，a3b3的长度分别为 l1，l2，l3。由于定平台和动平台均为正三角形，所以定平台中三顶点在坐标系oa-xayaza坐标为:

同理，动平台三顶点在ob-xbybzb坐标为:

由于定平台和动平台始终保持平行，所以动坐标系oa-xayaza相对于坐标系oa-aayaza的齐次变换矩阵为［4］:

其中，(xb，yb，zb)为动坐标系的原点ob在基础坐标系oaxayaza中的坐标。

根据坐标变换理论，动平台三个顶点在基础坐标系oa-xayaza中的位置可表示为［5］:

其中，bi＇是 b1，b2，b3在坐标系 oa-xayaza中的位置坐标；bi是b1，b2，b3在ob-xbybzb中的位置坐标。由两点距离公式得:

其中，c=R-r ，(xb，yb，zb)为动坐标系的原点 ob在基础坐标系oa-xayaza中的坐标。该式子成为3-TPT并联机构运动学逆解表达式［6］。其正解表达式为:

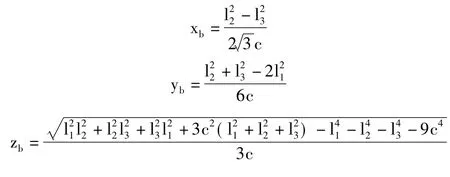
3.1 SimMechanics仿真模型

SimMechanics［7］是Simlink模块下一模块，其作用是为用户提供刚体、关节、约束和驱动以及传感器和驱动器等机构的模块，能对各种运动副连接的刚体进行建模仿真。SimMechanics还可以连接Simlink模块中的控制模型，提供机电一体化的建模仿真环境，为研究3-TPT并联机构提供了很大方便。

并联机构SimMechanics简图如图 3［8-9］所示，伸缩杆如图 4［10］所示。

图3 并联机构SimMechanics简图

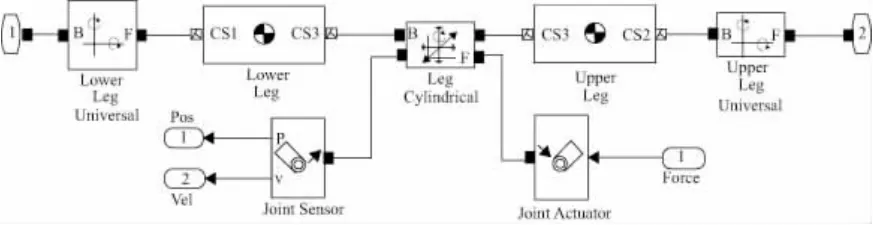
图4 驱动杆SimMechanics简图

图4 中Platform为动平台，通过伸缩杆与Ground模块相连，Env模块代表机构工作环境，通过该模块可以设定重力加速度向量、分析模式和容许误差等等，这个模块是所有SimMechanics模型必须具备的。F为Force的输入模块，输入Simulink信号；P和V模块分别代表Position和Velocity，分别用以检测位移和速度变化。

图5中两个Universal模块为万向铰(两个自由度，旋转两个角度)，Cylindrical为柱面铰。Jiont Acuator为激励信号输入模块，可以向关节或构件施加力或运动，其输入为外部Simulink信号接口。Joint Sensor为关节传感器，向用户提供了位置、速度、加速度以及力矩等信息，同时也可以连接Simulink中的示波器来观察这些数据［11］。

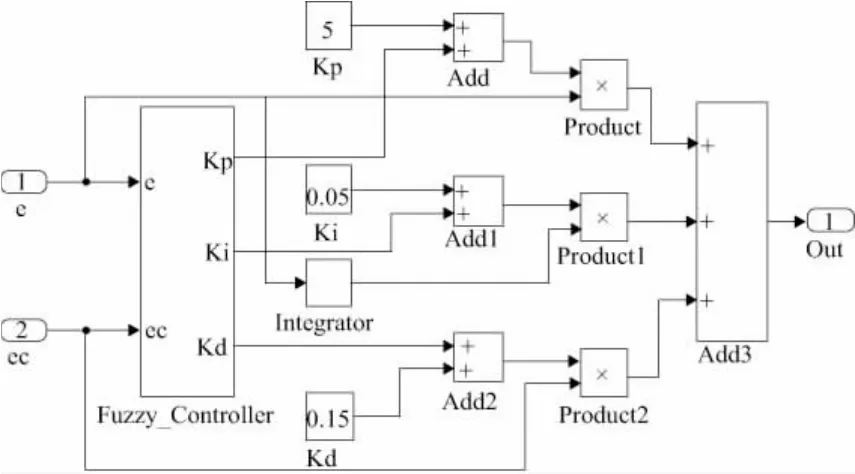
图5 模糊PID控制器

3.2 模糊PID控制器设计

模糊控制是利用模糊数学的基本理论和方法，把规则的条件和操作用模糊集表示，并把这些模糊控制规则以及有关信息作为知识存入计算机知识库中，然后根据控制系统的实际响应情况，运用模糊推理，即可自动实现对PID参数的最佳调整，这就是模糊PID的控制如图5［12］所示。本文把模糊控制和PID控制结合起来，利用模糊PID控制器对3-TPT并联机构进行设计和仿真，得到较好的控制效果。

利用Simulink对模糊PID进行建模设计。首先完成模糊控制器的设计，利用Matlab模糊控制箱设置论域和隶属度函数类型，输入控制规则，然后将其输出到Workspace中，最后封装子模块Fuzzy_Controller。图5中Kp，Ki，Kd为PID控制初始值，利用Simulink建模优势在于可以随时更改参数观察曲线变化，分析各参数对结果的影响。最后将整体封装，作为核心控制器输入到整体控制系统中［13］。

图6为并联机构整体控制系统，Leg Tracjectory为驱动单元，提供输入信号；Fuzzy_PID_Controller为模糊PID控制器，对输入的信号进行精准计算再输出到平台中。Plantform为图3封装后的子模块，即3-TPT并联机构示意图。令模糊因子ke=4，kec=30，解模糊因子k1=0.5，k2=0.1，k3=0.2，PID参数为Kp=5，Ki=0.05，Kd=0.15，得出曲线如图7所示。由图可知，模糊PID控制跟单独PID控制相比，优势比较明显:响应速度快，调节时间短，超调较小，控制效果比较理想。但模糊PID控制存在一定的稳态误差。模糊控制用模糊集合和模糊概念描述过程系统的动态特性，根据模糊集和模糊逻辑来做出控制决策，在解决复杂控制问题方面有很大的潜力，可以动态地适应外界环境的变化。

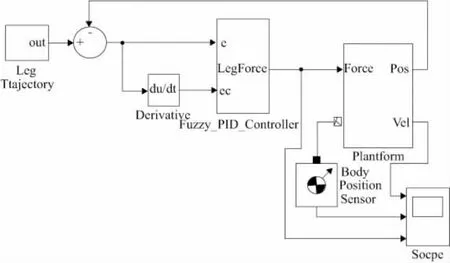
图6 并联机构控制系统

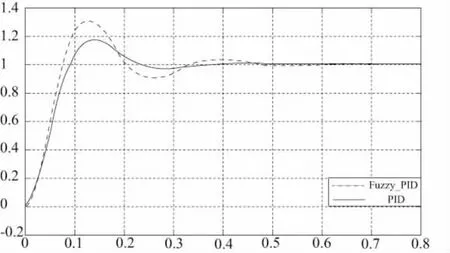
图7 对比曲线

4 仿真

令R=600mm，r=200mm，设定三杆运动方程为:

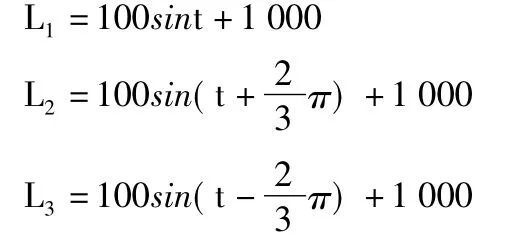
仿真结果如图8所示，可以看出:伸缩杆速度曲线变化平稳，曲线较为平滑，调节时间段、响应速度快、超调小，但存在一定误差。这些现象说明该机构平稳性较好，适合连续工作。

图8 伸缩杆速度变化曲线

5 结语

基于SimMechanics的并联机构仿真，在建立数学模型比较困难的情况下，可以较为简便的帮助设计者完成设计目的。其优势在于机构运行可视化，可以方便直观的了解仿真过程的输入输出的对应关系，检验设计参数的正确性。本文通过对3-TPT并联机构的认真学习研究，得出了正解逆解的表达式；通过Matlab中的SimMechanics模块建立并联机构模型，利用Simulink设计模糊PID控制器，并将二者相连接对整体结构进行了仿真模拟分析，得出了较为该并联机构较为平稳的结论，为日后更为深一层的研究学习打下了坚实基础。

［1］金云龙.并联机床的研究现状和发展前景［J］.企业技术开发，2010，29(6):128-129.

［2］程仙国，赵恒华.基于Matlab对3-TPT并联机床的运动学仿真［J］.辽宁石油化工大学学报，2008，28(1):19-22.

［3］王传强，赵恒华.3-TPT并联机床奇异性及平稳性研究［J］.组合机床与自动化加工技术，2010，36(10):26-28.

［4］杨辉，赵恒华，付洪栓.并联机构虚拟样机的构建与仿真［J］.工程设计学报，2012.

［5］吕春梅，谢里阳.3-TPT型并联机床仿真分析与研究［D］.沈阳:东北大学，2005.

［6］左扣成，谢里阳.3-TPT型并联机床误差分析与仿真［D］.沈阳:东北大学，2005.

［7］胡蜂，骆德渊，段栋栋，等.基于Pro/E与Simulink的Delta并联机器人运动仿真［J］.机电工程，2012，29(8)982-984.

［8］李志斌，董旭明，钟德勇.基于SimMechanics的三自由度并联机器人仿真［J］.工业控制计算机，2012，25(8)88-93.

［9］孙坚，丁永生，郝矿荣.基于SimMechanics的新型并联机构仿真平台［J］.计算机仿真，2010，27(1)，181-184.

［10］杨树川，邵金龙，杨术明，等.基于 Solidworks＆SimMechanics的机构运动分析与仿真［J］.河北工业科技，2011，28(4)，221-225.

［11］王英波，黄其涛，郑书涛，等.Simulink和SimMechanics环境下并联机器人动力学建模与分析［J］.哈尔滨工程大学学报，2012，33(1)，100-105.

［12］刘义德，丛大成.基于并联机构的稳定平台建模与控制［D］.哈尔滨:哈尔滨工业大学，2009.