RLC暂态过程震荡峰位对测量时间常量的影响

王国菊,吕太国,牟 娟

(聊城大学 物理科学与信息工程学院,山东 聊城 252059)

摘要：在测量RLC电路暂态过程时间常量时，通常测量电容电压的欠阻尼震荡峰值间接测量时间常量. 欠阻尼震荡峰值往往简单地近似为sin (ωdt+φ)=±1时的电容电压值. 讨论了这一近似峰位与准确峰位的区别与联系，结果表明由近似峰位得出的时间常量不存在近似性，与由准确峰位得出的时间常量是一致的.

关键词：RLC暂态；时间常量；欠阻尼震荡

中图分类号：TM935文献标识码：A文章编号：1005-4642(2014)08-0028-03

1 引 言

“RLC串联电路暂态过程的研究”是电磁学实验的必做实验，其中欠阻尼情况下暂态过程时间常量的测量是实验的重要内容，正确测量时间常量是了解RLC电路特性的前提. 文献指出sin(ωdt+φ)=±1时欠阻尼震荡为峰值[1-7]，这只是一种简单近似. 按照这种近似条件求得的时间常量是否也是近似结果呢？下面以电容器上的放电过程为例讨论时间常量的测量.

2 测量方法及分析

在RLC串联电路中，设电源电压为0～E的方波电压，则电路的放电过程回路方程为

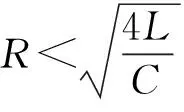
(1)

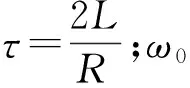
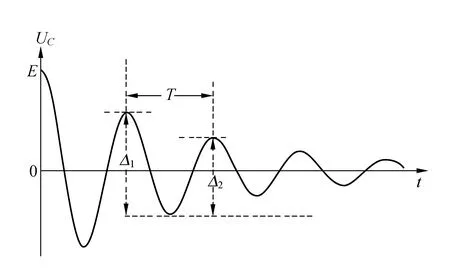
图1 电容放电曲线

若认为震荡峰值出现在sin (ωdt+φ)=±1时，可用以下2种方法通过测量震荡峰值求时间常量τ.

方法1：由线性回归方程的斜率求时间常量.

由(1)式，UC为正最大值时，

(2)

两边取对数得：

(3)

测出几组(UCm，t)，作lnUCm-t的直线，利用图解法求斜率可得到时间常量τ.

方法2：测量任意两振幅比值求时间常量.

根据(1)式，测量任意振幅UCm1及相隔nT时间衰减后的振幅UCm2，则

(4)

两边取对数得

(5)

再测出欠阻尼震荡周期T，可求出时间常量τ.

也可由相邻的两峰谷电压差的比值测量时间常量. 根据图1，测出相邻的两峰谷电压差Δ1和Δ2. 由放电方程 (1)式可知，

两式相除得：

(6)

测出Δ1,Δ2和T，即可求出时间常量τ.

以上方法是把sin (ωdt+φ)=±1对应的电压看作衰减震荡的峰值，这是把(1)式看作简单函数的粗略近似. 这种近似结果显然与求解(1)式时所依赖的初始条件相矛盾，对学生理解震荡过程造成一定的困难.

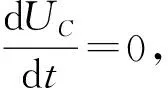
(7)

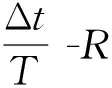
图2 Δt/T与R的关系曲线

(8)

因此需要对以上2种时间常量的测量方法进行修正. 用方法1测量时，(3)式变为

(9)

(9)式与(3)式相比较，直线的截距改变了，而斜率不变，因此时间常量的测量结果不变. 用方法2测量时，对比(2)式和(8)式，振幅系数发生了变化，而振幅系数的改变对振幅比没有影响，测量的时间常量也就不会变化. 因此尽管衰减振荡的峰值不是出现在sin (ωdt+φ)=±1时，但在这种近似下求得的时间常量却是正确的.

3 结 论

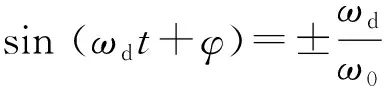
参考文献：

[1] 杨述武,杨介信,陈国英，等. 普通物理实验(二、电磁学部分)[M]. 北京:高等教育出版社，2000:288-297.

[2] 朱世嘉.RLC串联电路暂态过程中的几个问题[J]. 大学物理,1988,7(6):23-24.

[3] 曹伟然. 用示波器测RLC电路暂态过程的时间常数[J]. 临沂师范学院学报,2005,27(6)：138-139.

[4] 王新礼.RLC串联电路暂态过程和τ值的修正[J]. 北华大学学报(自然科学版)，2005,6(5)：396-398.

[5] 桂维玲.RLC并联电路暂态过程临界电阻测量的新方法[J]. 山东师范大学学报(自然科学版),2007,22(4):132-133.

[6] 丁菲，刘平安. 大学物理实验[M]. 开封：河南大学出版社，2009:206-209.

[7] 陶向阳，燕安. 基础物理实验教程[M]. 南昌：江西教育出版社，2007：101-106.