驻波法之声压极小值测声速研究
2014-09-12田玉仙李绍蓉
田玉仙,李绍蓉,陈 丹,龚 安,杨 易
(西安科技大学 理学院,陕西 西安 710054)
1 引 言
对于驻波干涉法[1]测声速的实验原理,教材只是简单推导了两行波叠加形成的驻波方程,利用驻波相邻波节间距离是半个波长,记录下示波器显示的正弦波振幅最大时接收器坐标,逐差法处理数据即可计算波长,从而测定声速. 但学生不明白形成稳定驻波时,接收器处恒为波节,振幅应该恒为零,为什么测定示波器显示的正弦波振幅最大时接收器坐标,就可以测定波长……,二者间有何联系?利用该法测试声速中,示波器显示的正弦波常超出示波器屏幕范围,导致振幅最大无法判断,为让实验得以进行,只能随时减小示波器Y偏转增益,这样又会增加实验误差,对此问题如何解决?朱方玺等[2]针对原有声速测量仪中存在的不足,利用单片机、步进电机等器件构建控制电路,通过识别信号强度强弱变化来代替原有实验仪中手动操作,提高了实验精度. 郑庆华[3]分析了考虑空气对声波的吸收及反射截面损耗下利用相邻两声压极大值之间的距离为λ/2测声速的原理. 王开圣等[4]分别导出了平面波、球面波函数下考虑空气吸收后接收声压的表达式,分析了声压随探头间距的变化规律. 张宝峰等[5]对声波在发射器和接收器2个端面之间反射形成极大值的位置、条件以及声波强度随距离变化的规律作了研究. 张正康等[6]介绍了基于Cassy Lab软件下的超声波干涉实验,根据干涉理论推导了峰谷法测量声速的计算公式.从文献[4,5]中声强随距离变化实验、模拟图片都可以看出,共振干涉法测声速时,声压极小值也按接收器位置呈半波长的周期性变化,对此,二文献均未提及. 文献[6]虽然提出了干涉峰谷法测量声速理论,但其采用了与现行绝大多数工科院校大学物理声速实验完全不同的仪器设备,因此不具有可比性。本文将针对工科院校大学物理实验中驻波干涉法测声速常规仪器设备,详细详细推导无数往返行波叠加形成的稳定驻波方程和驻波的能量方程,将之与压电陶瓷声电转换理论结合起来,从而揭示形成稳定驻波时示波器显示正弦波形振幅与接收器媒质能量关系,看从理论上找到声压极小值法测声速的依据并用实验验证.
2 驻波方程的推导
驻波法测声速实验装置如图1所示. 实验前,调节接收器S2,使之与发射器严格平行且同轴等高,并选择性能较好的输出频率稳定的低频信号发生器. 当信号发生器输出正弦波信号,接至压电陶瓷超声波换能器(电声转换)S1,发射出超声平面波(声源). 该超声波经空气正向入射到相距一定距离L的压电陶瓷接收器(声电转换)S2后,将沿发射器和接收器轴线在接收器表面作垂直反射,形成逆向反射波,该反射波逆向传输至发射器时,又会沿二者轴线在反射器表面垂直反射,发出二次正向入射波,接着又会在接收器表面垂直反射,形成二次逆向反射波……如此往返地传播,S1和S2之间可有无穷多个正向入射行波和逆向反射行波传播着.由于空气的阻抗小于铝材料制成的压电陶瓷换能器阻抗,故在发射器和接收器表面的每次反射中都存在半波损失. 由于超声波声强随距离增加衰减较小,可忽略空气对超声波能量的吸收. 反射端面很平整、光滑且同轴等高,反射界面的能量反射损失也可以忽略.
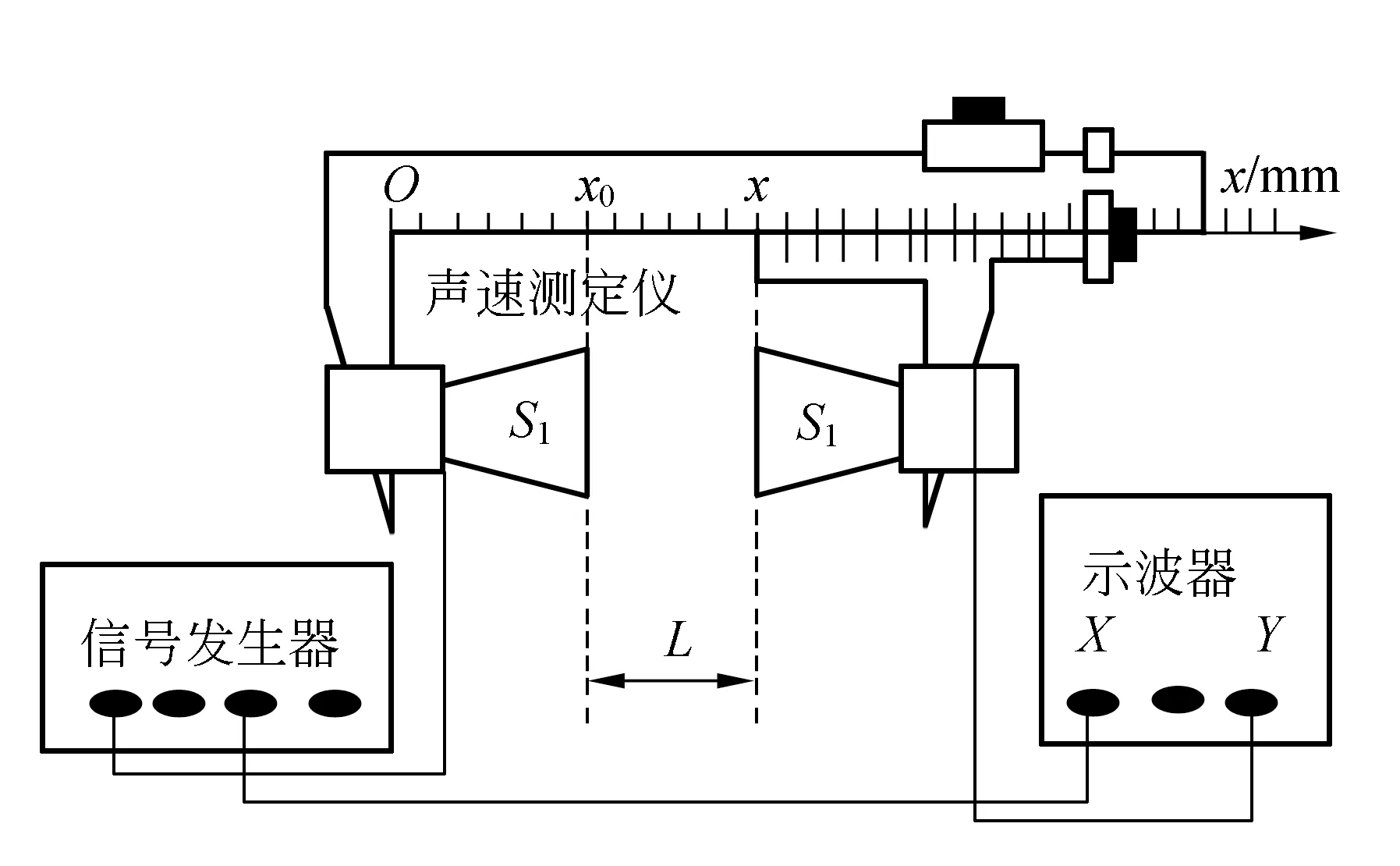
图1 驻波干涉法测声速连线图
选择游标卡尺主尺0线为坐标原点,沿游标尺方向建立x轴,声源S1坐标x=x0,选择适当的计时零点使1次入射波初相为零,则各次理想的正向入射波和逆向反射波波函数为
(1)
(2)
(3)
(4)
(5)
(6)
x为各媒质位置坐标,可从游标卡尺读出.
从各次正向入射波和逆向反射波波函数可以看出,当发射器和接收器端面之间的距离L=nλ/2时,所有正向入射波、逆向反射波分别同相位,相互叠加后各自的合成波振幅都取最大值. 把所有正向入射波等效为一列波y入,把所有逆向反射波等效为一列波y反,则得到稳定驻波波动方程为

(7)
3 驻波的能量
在发射器S1和接收器S2间任意取一体积元dV=Sdx,S是媒质截面积,dx是体积元线度. 设空气密度为ρ,杨氏模量为Y(Y=ρu2),正向入射波和逆向反射波传输过程中,都会引起该体积元振动并发生形变,引起振动动能和形变势能的改变. 其振动速度、形变量、振动动能、形变势能和机械能分别为
(8)
(9)
(10)
(11)
dW=dWk+dWp.
(12)
由上述计算公式知,各体积元的振动速度、形变量、动能、势能和机械能都随时间作同周期性的变化. 结合图2和图3可以看出,波节处,振动速度始终为零,体积元始终保持静止,动能为零,而其形变量及形变势能均随时间按照余弦规律作同周期性变化.t=(2k+1)T/4时形变量及势能最大,最大势能值为dWp-max=2ρA*2ω2Sdx,t=2kT/4时形变量为零,势能为零.
波腹处,体积元形变量始终为零,势能始终为零,但其振动速度及动能也随时间按照余弦规律作同周期性变化.t=2kT/4时振动速度最大,动能最大,最大动能dWk-max=2ρA*2ω2Sdx,且dWk-max=dWp-max,t=(2k+1)T/4时振动速度为零,动能为零.

图2 波节处∂y/∂x及波幅处v随t变化
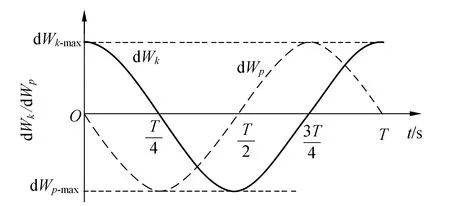
图3 波节处dWp及波幅处dWk随t变化
相邻波节和波腹之间媒质的总能量
(13)
不随时间变化. 也就是说,任一相邻波腹和波节间λ/4长的一段驻波,作为一个整体,其能量变化与谐振子类似,波节处只有势能,波幅处只有动能,且波节处媒质最大形变势能与波幅处媒质最大振动动能相等,在任一时刻,波节处2波的能流密度矢量大小相等,方向相反,叠加后能流密度矢量为零,波腹处的能流密度矢量也为零,即无能量流过波节和波幅.而波节和波幅间的其他媒质,既有势能又有动能,驻波的势能和动能在相邻波节和波幅间相互转化,转化周期刚好为波动周期的T/4,驻波无能量的定向传播.
4 声压方程
本实验中,超声波的发射和驻波信号的接收都是通过压电陶瓷换能器来完成的. 压电陶瓷换能器由压电陶瓷片和一轻一重2种不同金属组成,在一定的温度下经极化处理后,具有压电效应,利用它能够将机械能和电能互相转换. 当正弦交流电信号加到发射器上时,会引起压电陶瓷振动并产生伸缩形变,发射超声波.当超声波正入射到达接收器时,会在接收器表面垂直反射,二者都会引起组成接收器的压电陶瓷换能器振动,在纵向上发生伸缩形变,并在形变的相反方向上产生与形变量成正比例的弹性压力(应力),设应力的合力F=-k∂y/∂x. 在此应力作用下,压电陶瓷表面会产生电荷,而在极化方向上产生一定的电压U(声压),该声压U与应力F满足线性关系
(14)
该式也是声学理论中所述的一维情况下,忽略媒质对声波吸收时接收器端面处的声压波动方程[7],比例常量k和ks分别为弹性系数和压电常量,与材料性质有关. 压电陶瓷就是通过这种方式,将声压变化转变为电压变化来接收声信号的.
综上所述,当声速测定仪的发射器和接收器端面之间的距离L=nλ/2时,发生器和接收器间可形成稳定声驻波,由于反射时有半波损失,此时接收换能器表面处始终为波节,媒质始终静止不动,振幅为零,位移为零,故本实验中示波器显示的波形实际上不是接收器端面波节的位移波形. 从图1可知,声速实验中,是将接收器接收到的声电转换信号直接接到示波器Y端,选择示波器Y工作模式,故示波器屏幕上显示的正弦波形正是由接收器压电陶瓷伸缩形变产生的声压波形. 由声压波动方程可看出,声压的值随接收器位置呈周期性变化,波幅处,声压为零,波节处,声压随时间按照余弦规律呈周期性变化.t=(2k+1)T/4时,媒质形变量最大,势能最大,接收器接收到的声电转换信号U最大,示波器上显示的正弦波形振幅也最大,声压效应最明显.t=2kT/4时,媒质形变量为零,势能为零,理论上接收器接收到的声电转换信号U应该为零,示波器上显示的电信号振幅也应该为零.
5 声速的测量
5.1 实验仪器
采用杭州大华仪器制造有限公司生产的SV-DH-7声速测定仪,共振频率f=37 090 Hz;SUX-5型综合声速测定仪信号源,输出频率范围25~45 kHz;自配示波器为西安红华电子有限公司生产的20 MHz双踪示波器,型号为红华COS 5020B,最高灵敏度1 mV/div. 声速测量组合仪实物照片见图4.

图4 声速测量组合仪实物照片
5.2 传统声压极大值法测声速
移动接收换能器位置,接收器接收到的声压极大值将随S1和S2间距离L呈周期性变化. 因此,若保持声源的频率f不变,移动接收器,改变接收器与发射器间的距离L,则在一系列的距离上可不间断地测得接收器处声压振幅极大值的位置坐标x1,x2,x3,x4,…,x12. 根据相邻两声压极大值之间接收器位置坐标改变量xi+1-xi=λ/2,采用逐差法,可求出该超声波在空气中的波长λ,再用公式u=λf可计算出该超声波在空气中的传播速度.这也是现有的大学物理实验教材中,驻波干涉法测声速实验所采用的通用办法.
驻波共振干涉法测定声速中,当接收器接收到超声波强度的大小发生微小变化时,示波器能否反映出来,取决于示波器Y偏转的灵敏度和幅度线性.Y偏转增益越大,示波器的灵敏度越高,幅度线性越好,就越能反映超声波强度大小的微小变化,测量结果也就越精确. 而传统的声压极大值法所显示的声压波形幅度受示波器显示屏大小及几何尺寸的制约,即波形不能超过屏幕的最大尺寸,否则就无法观察和比较波形和幅度,所以Y偏转增益不能过大.故一般示波器的最高灵敏度为1 mv/div,误差为10%[8].
5.3 声压极小值法测声速
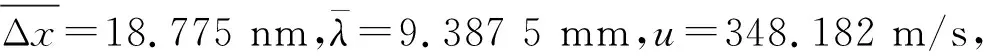
由于超声波在空气中传播时,其能量要被空气吸收衰减,振幅也要衰减,而低频超声波在空气中吸收系数较小,这使得声波衰减速度慢,这样反射波振幅总小于入射波,但入射波与反射波的振幅相差不大,干涉叠加并形成稳定驻波时,接受器处媒质实际的形变量、弹性势能的极小值不可能为零,示波器接收到的声压的极小值也不为零,这与前面对理想驻波推导不符,实验时需仔细观察.

表1 驻波法之声压极小值法测声速数据
声压极小值法不受示波器显示屏大小及几何尺寸的制约,为提高仪器灵敏度,实验前可将示波器Y偏转增益调到最大,即可使实验误差减少到仪器所能达到的最小程度.
6 结 论
示波器屏幕上显示的正弦波形为声压波形,其值与接收器压电陶瓷形变量成正比.t=(2k+1)T/4时最大,t=2kT/4时最小. 连续监测系列声压极大值或极小值时S2位置坐标,利用相邻两声压极大值或极小值间接收器位置坐标改变量都是λ/2,采用逐差法,兼可测定超声波波长,从而测定声速. 与传统声压极大值法相比,声压极小值法测声速不受示波器显示屏大小的限制,实验前如将Y偏转增益调到最大,可大大减少实验误差,因此,该法更具有优势.
参考文献:
[1] 炎正馨. 大学物理实验教程[M]. 西安:西北工业大学出版社, 2011:123-129.
[2] 朱方玺,曹伟然. 声速测量实验仪的改进[J]. 物理实验,2011,31(10):40-43.
[3] 郑庆华. 声速测量实验的探讨[J]. 大学物理,2007,26(9):31-33.
[4] 王开圣,赵志敏,刘小廷. 声速测量实验原理讨论[J]. 物理实验,2010,30(3):25-28.
[5] 张宝峰,刘裕光,张涛华. 声速测量实验中界面反射问题的探讨[J]. 物理实验,2001,21(8):10-12.
[6] 张正康,周天赐,韩杰克,等. 基于超声波干涉的峰谷法计算声速值及实验误差探讨[J]. 物理实验,2011,31(4):42-45.
[7] 何祚镛,赵玉芳. 声学理论基础[M]. 北京:国防工业出版社,1981:25-29,237-259,315-326.
[8] 上海新建仪器设备有限公司. XJ4318型双踪示波器技术说明书[Z]. 上海.
