计及输入变量强相关性的概率潮流计算模型

别 佩，张步涵，邓韦斯，吴俊利，曾远方

（华中科技大学强电磁工程与新技术国家重点实验室，湖北武汉 430074）

计及输入变量强相关性的概率潮流计算模型

别 佩，张步涵，邓韦斯，吴俊利，曾远方

（华中科技大学强电磁工程与新技术国家重点实验室，湖北武汉 430074）

利用统计学的方法，以风电场出力为例，对其大量历史数据进行相关性分析，将具有强相关性的随机变量用最小二乘进行线性拟合，并用其中一个变量的线性表达式表示，从而消去随机变量之间的强相关性，并认为余下的呈弱相关或不相关的随机变量之间相互独立，以便采用半不变量法计算概率潮流。

风电；概率潮流；半不变量法；相关性；最小二乘法

现代电网中，可再生能源（如风电、光伏发电）越来越多地应用到发电系统。它们具有随机性、间歇性和波动性的特点，加剧了系统的不确定性。如何实现多元能源系统间的良性互动和各种资源的综合高效优化利用，是当前和未来都需要解决的重要课题。“源—网—荷”互动（电源、电网、负荷相互之间良性互动）是应对未来电网能源结构变革的重要手段，也是未来电网快速发展的必然趋势［1］。

潮流计算是电力系统稳态分析的基础。传统的确定性潮流计算需要负荷节点功率、发电机节点注入功率的确切值，且只能反映电力系统在某种确定工况下的稳态运行状况，不能用于计及不确定性因素场景的分析。考虑系统的不确定性因素计算潮流的主要方法有概率潮流、区间潮流和模糊潮流。其中，概率潮流将不确定性变量表示为呈一定概率分布的随机变量，根据输入的随机变量的概率特性求出各节点电压幅值、相角和线路潮流的概率分布，相比模糊潮流和区间潮流，概率潮流能给出更为全面的电网信息。而解概率潮流方程的过程就是根据输入随机变量的期望、方差或概率分布来确定输出随机变量的期望、方差或概率分布［2］。

目前，概率潮流的计算方法主要有蒙特卡罗模拟法（Monte Carlo simulation method，MCSM）［3］、点估计法（point estimate method，PEM）［4］和卷积法［5－7］。蒙特卡罗模拟法是一种包含了状态变量（节点电压和幅值）和支路潮流的概率密度函数的算法，它通过对输入随机变量的概率分布重复采样，从而得到一系列样本，然后进行多次确定性潮流计算，最终得到输出变量的统计分布特性。尽管当采集样本足够大时，蒙特卡罗模拟法可以得到较为精确的解，但是十分耗时，并不适用于系统的在线实时应用。通常将蒙特卡罗模拟法更多地作为标准验证其它概率潮流计算方法的准确性。点估计法虽然有较快的计算速度，但是输出变量的高阶矩误差较大［8］。卷积法通过将潮流方程线性化，将状态变量和支路潮流用输入变量的线性表达式表示，但是计算量大，需要大量存储空间和时间开销，同样不适合大系统求解。

采用半不变量法计算概率潮流则具有计算简单和计算速度快等优点，该方法用Gram－Charlier展开级数来拟合输出随机变量的概率密度函数，能大大减小所需的存储空间，因此非常适合用于实时在线系统中。但该方法要求各个输入随机变量之间相互独立。随着新能源的大规模并网，这个条件并不总能满足。以风电为例，当几个风电场的地理位置较为接近时，它们的出力就具有明显的正相关性，因此无法直接利用半不变量法求解。

为此，本文利用统计学的方法，对电力系统中的不确定因素进行相关性分析，并以风电为例，近似认为风电出力服从正态分布。将具有强相关性的随机变量进行线性拟合，从而减少随机变量元，并近似认为具有弱相关性的随机变量之间相互独立。

1 相关性分析方法

1.1 相关性分析概述

相关性分析是指对两个或多个具备相关性的变量元素进行分析，从而衡量两个变量因素的相关密切程度。未来电网的一次能源具有多样性（如水电、风电、光伏发电、生物质发电、海洋能发电等），其时空分布和动态特性均存在一定的相关性。为避免寻找电力系统中各部分复杂的内部相互关联的机理，可以从统计学角度出发，对大量历史数据进行相关性研究。相关性分析的主要内容包括：确定现象之间是否存在相关关系以及相关关系的表现形式、确定相关关系的密切程度、确定相关关系的数学表达式，即回归方程式和验估计值的误差。

与函数关系不同，函数关系是指现象间所具有的严格的确定性的依存关系，而相关关系是指客观现象间确实存在关系，但数量上不是严格对应的依存关系。电力系统中的随机因素有很多，近年来由于风电的迅速发展和大规模并网，风电已经成为“源—网—荷”互动环境下不确定因素中极为重要的一个部分。本文以风电为例，来研究不同风电场出力的相关性及其在概率潮流中的应用。

1.2 相关性分析数学描述

设随机变量y与x之间存在着某种相关关系。这里x是可以控制或可以精确测量观测的普通变量。对于x取定的一组不完全相同的值x1，x2，…，xn，作独立试验得到n对观测结果：

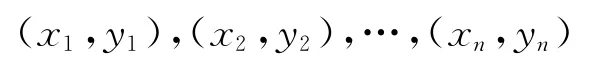
其中yi是x＝xi（i＝1，2，…，n）处对随机变量y观测的结果。这n对观测结果就是一个容量为n的样本，将每对观测值（xi，yi）在直角坐标系中描出相应的点，得到试验的散点图。在这n个点之间尽量地拟合出一条光滑曲线，使这n个点尽可能地“接近”这条曲线，并可以认为该曲线的方程反映了y与x的相关关系。

在直线相关的条件下，用以反映两变量间线性相关密切程度的统计指标，用r表示

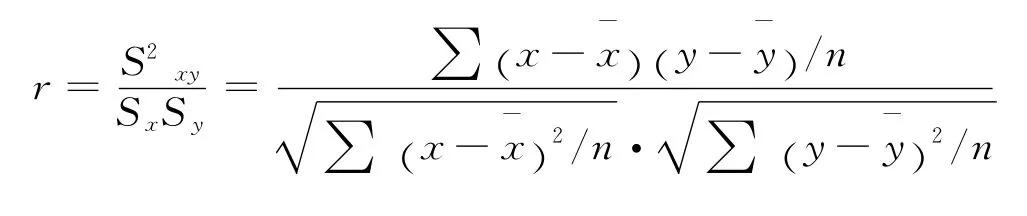
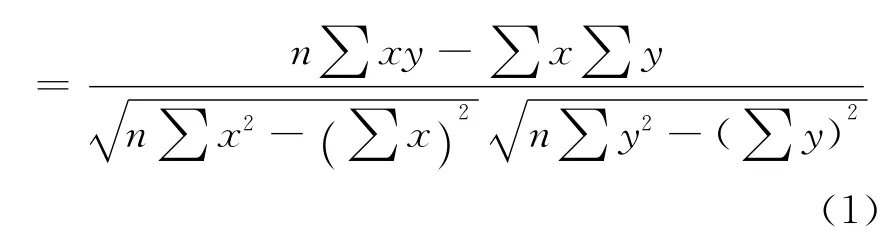
式中，Sx、Sy分别为随机变量x与y的标准差，S2xy为x与y的协方差。

若两个随机变量的相关系数很高（比如大于0.9），那么就可以用最小二乘法拟合出一条直线，指定x为自变量，那么y就可以用x的线性表达式y＝a＋bx来表示。表达式中参数的确定如下式所示：

2 考虑输入变量强相关性的半不变量法模型修改

潮流问题可以用下面两个非线性的方程组描述：

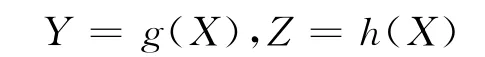
其中，X为节点电压幅值和相角；Y为节点注入有功和无功功率；Z为未知输出变量向量（网络元件的有功和无功功率潮流）；g、h为潮流函数。

将式（1）在X0处线性化，得到：

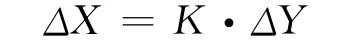
式中K＝－J－1（X0）是基于X0的雅克比矩阵的逆矩阵

对于输出变量Z，可以通过相同的方式得到Z和Y之间的线性关系。然后将式（1）、（2）在点（X0，Y0）和（X0，Z0）线性化得到

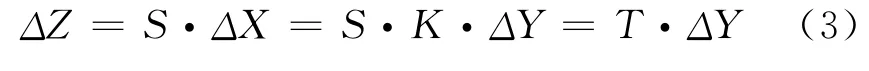
对于有n个节点的系统，假定第1～m号节点为PQ节点，第m＋1～n－1号节点为PV节点，第n号节点为平衡节点。则可列写如下的潮流方程式：

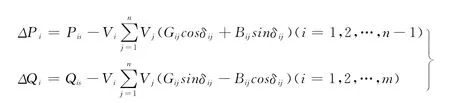
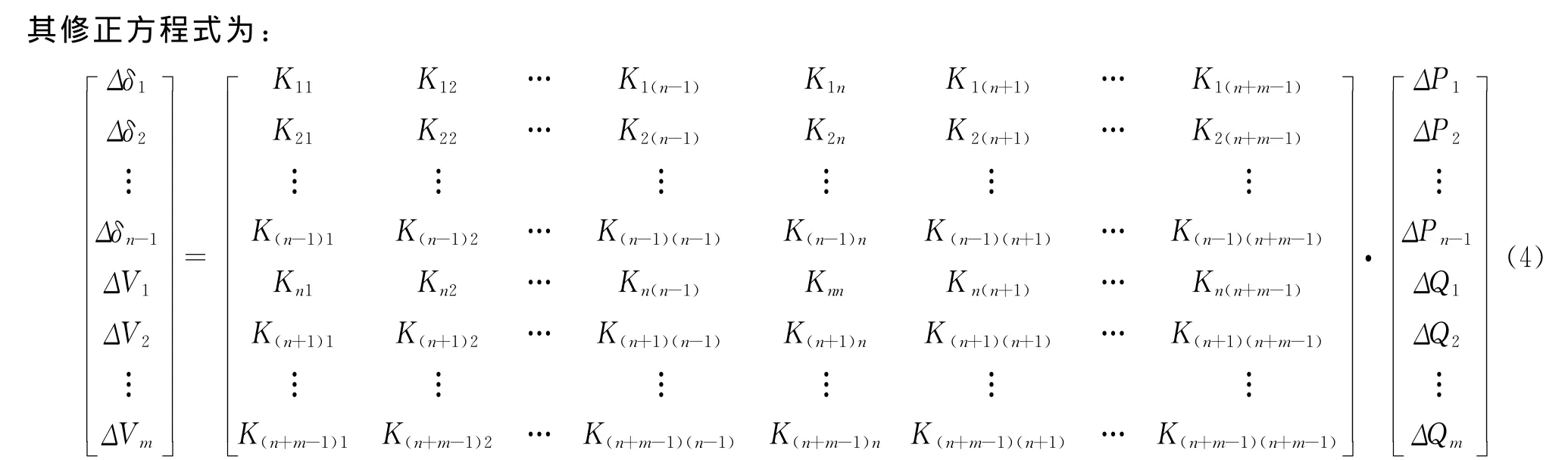
现假定节点1、节点2为风电节点，ΔP1、ΔP2均为服从正态分布的随机变量，且其期望为0。并假设这两个风电场出力具有强相关性，而其它节点功率相互独立。因此可近似认为ΔP2＝bΔP1，参数b可以通过式（2）计算得到（由于两个随机变量的均值为0，因此参数a＝0）。这样，修正方程应该修改为：

记修改后的灵敏度系数矩阵为K′，同理修改式（3）中的灵敏度系数矩阵得到T′，从而消去了随机变量ΔP2，剩下的随机变量均相互独立，因此可以采用半不变量法进行求解。

3 算法流程

针对节点注入功率具有强相关性的情况，通过线性拟合来消去强相关性的随机变量元，从而满足半不变量法求解概率潮流的要求。计算步骤如下：

1）输入原始数据，包括支路参数、发电机及负荷注入功率等一般潮流计算所需的数据，此外还要求给出有关节点注入量随机分布的信息，例如对正态分布的负荷和风机出力要给出其期望值和方差等。

2）用确定性潮流计算方法给出正常运行情况的潮流分布，从而求得在基准运行点上的状态变量X0、雅可比矩阵J0，求出灵敏度矩阵K0。

3）对具有强相关性的节点注入功率进行线性拟合，并按照式（4）修改修正方程，得到修改后的灵敏度系数矩阵K′。

4）计算各个独立输入随机变量的原点矩或者中心矩，进而求出各阶半不变量。并由此求出ΔX、ΔZ的各阶半不变量。最后应用Gram－Charlier展开级数，求出状态变量和支路功率的随机分布［9］。

计算流程图见图1。

图1 计算流程图

4 算例分析

现通过研究不同风电场出力之间的相关性来具体说明本文对强相关不确定因素的处理方法。取三个已知一整年出力的风电场功率数据，数据均取自美国可再生能源实验室（NERL）公布的风电出力数据。利用SPSS软件计算每个风电场出力两两之间的相关系数，得到的相关矩阵见表1。

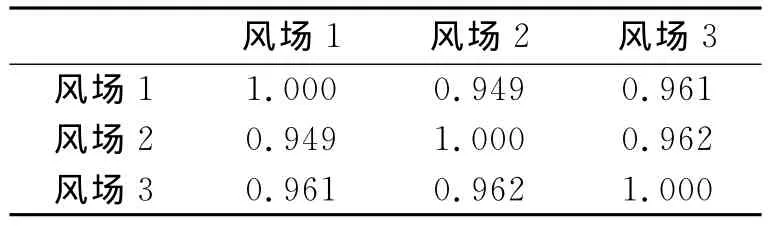
表1 相关矩阵

可以看到，这3个风电场出力的相关系数都很高，均大于0.9，故其相关性很强。以风电场1和风电场2为例，采用最小二乘法得到线性回归方程为：

y＝0.985x其中x表示风电场1的出力与期望的差值，y表示风电场2的出力与期望的差值。

这样，在后续计算中，变量y均用0.985x表示，即式（5）中的b＝0.985。同理也可对风电场3的出力进行处理。这样，就可以消去强相关因素随机变量元，而剩下的随机变量都相互独立，满足半不变量法计算概率潮流的要求。

5 总结

现代电力系统中新能源发电和柔性负荷的接入，使得系统的随机性和不确定性大大增加，难以采用一个确定的模型来进行描述。利用统计学的方法。对电力系统中的电源出力值、负荷值的大量历史数据进行相关性分析，可以避免寻找电力系统中各部分复杂的内部相互关联的机理，而只从数据本身出发，得出较为直观的结论。

本文通过分析风电场出力数据，得出有些风电场的出力相关性很强，通过最小二乘法拟合，将具有强相关性的随机变量用其中一个变量的线性表达式表示，由于假定风电出力服从正态分布，因此不相关的随机变量就认为相互独立。通过消去具有强相关性的随机变量，从而减少随机变量元，同时近似认为剩下的不相关或呈弱相关的随机变量之间相互独立，就满足了采用半不变量法计算概率潮流的要求。该方法还可应用到常规电源和新能源之间、负荷与电源之间的分析当中，从而能通过半不变量法得出更为准确的概率潮流解。

［1］ 姚建国，杨胜春，王 珂，等.智能电网 “源—网—荷”互动运行控制概念及研究框架［J］.电力系统自动化，2012，36（21）：1－6.

［2］ 陈 雁，文劲宇，程时杰.考虑输入变量相关性的概率潮流计算方法［J］.中国电机工程学报，2011，31（22）：80－87.

［3］ 丁 明，李生虎，黄 凯.基于蒙特卡罗模拟的概率潮流计算［J］.电网技术，2001，25（11）：10－14.

［4］ Su C L.Probabilistic load－flow computation using point estimate method［J］.Power Systems，IEEE Transactions on，2005，20（4）：1 843－1 851.

［5］ Allan R N，Borkowska B，Grigg C H.Probabilistic analysis of power flows［J］.Electrical Engineers，Proceedings of the Institution of，1974，121（12）：1 551－1 556.

［6］ Allan R N，Al－Shakarchi M R G.Probabilistic ac load flow［C］／／Proceedings of the Institution of Electrical Engineers.IET Digital Library，1976，123（6）：531－536.

［7］ Allan R N，Grigg C H，Al‐Shakarchi M R G.Numerical techniques in probabilistic load flow problems［J］.International Journal for Numerical Methods in Engineering，1976，10（4）：853－860.

［8］ Usaola J.Probabilistic load flow in systems with wind generation［J］.IET generation，transmission ＆distribution，2009，3（12）：1 031－1 041.

［9］ 刘怡芳，张步涵，李俊芳，等.考虑电网静态安全风险的随机潮流计算［J］.中国电机工程学报，2011，31（01）：59－64.

［责任编校：张岩芳］

Probabilistic Load Flow Calculation Model Considering Strong Correlation between Input Variables

BIE Pei，ZHANG Bu－han，DENG Wei－si，WU Jun－li，ZENG Yuan－fang
（State Key Laboratory of Advanced Electromagnetic Engin.and Technology，Huazhong Univ.of Science and Tech.，Wuhan 430074，China）

Load flow is the basis of the steady－state analysis of the power system.However，the traditional power flow cannot be used in the system considering the uncertainty of the system.That′s why probabilistic load flow comes into being.Among different kinds of methods solving probabilistic load flow，the cumulant method is simple and has fast calculation speed.But it requires that the input variables should be independent，so it is necessary to analyze the correlation between input variables.In this paper，the statistic method was applied and the outputs of different wind farms were analyzed.If they have strong correlation，they can be expressed with only one random variable by using the least squares.Then the rest random variable which are irrelevant or has weak correlation can be considered independent，so that the cumulant method can be applied.

wind power；probabilistic load flow；cumulant method；correlation；least squares

TM 712

A

1003－4684（2014）01－0049－04

2013－11－28

别 佩（1990－），女，湖北宜昌人，华中科技大学硕士研究生，研究方向为电力系统分析计算