基于主成分分析的风电场等值方法的研究

曾远方，张步涵，吴俊利，别 佩，李 枚，赵 爽

（华中科技大学强电磁工程与新技术国家重点实验室，湖北武汉 430074）

基于主成分分析的风电场等值方法的研究

曾远方，张步涵，吴俊利，别 佩，李 枚，赵 爽

（华中科技大学强电磁工程与新技术国家重点实验室，湖北武汉 430074）

针对系统中含有多随机变量的问题，提出了采用主成分分析对多电源提取有效的主成分来进行等值，结合REI等值对网络进行化简的方法。算例分析中运用了主成分分析方法进行了多台风力发电机的主成分提取，将提出的主成分看成虚拟的等效风力发电机来替换原有的多台风电机组，实现了有效的简化替换，降低了系统分析的复杂性。

电力系统；主成分分析；等值简化；风电场；多随机变量

随着风能、太阳能等新能源在世界能源格局的比重不断增加，多种新能源的随机波动和复杂的网络结构对现代电力系统的影响越来越大［1，2］。电动汽车等柔性负荷并入电网，也增加了电力系统的复杂性，使得电力系统运行具有更为复杂的不确定性［3－5］。多随机电源、负荷以及系统规模的增大使得目前电力系统中存在大量随机因素，电网互联使得电力系统规模增加，不同运行方式下的分析计算也变得尤为复杂。因此，对于多随机因素的分析和电力网络的等值化简成了目前电力系统分析中的一个重要问题。电力系统的等值主要针对发电机组、电力网络、负荷的等值，等值的目的不外乎是为简化过于复杂的外部系统、除去不关心的部分，便于对所要研究的内部系统进行分析［6］。大规模风力发电中含有大量风力发电机和多个风力发电场，这使得电力系统的电源结构变得复杂并具有较强的随机性，增加了电力系统分析的复杂度和困难。本文运用主成分分析方法对含有多台风机的风电场进行了等值简化，通过对多台风力发电机的出力进行主成分分析，将提出的主成分看成虚拟的等效风力发电机来替换原有的多台风电机组，实现了有效的简化替换。

1 电力系统静态等值

一个互联的系统可以划分为研究系统和外部系统，研究系统指的是研究过程中感兴趣的区域，或者说是要详细计算模拟的电网部分，外部系统则是不需要详细计算的部分，或是运用某种等值方法来取代的电网部分［7］。外部系统等值可以分为拓扑结构等值和非拓扑结构等值。拓扑结构等值需要利用外部系统的结构和参数，通过消元、替换等措施来进行简化，而非拓扑结构等值则不需要利用系统的结构参数，而是根据测量数据来进行数据分析等值，是一种辨识法［6］。任何一种等值方法都必须满足以下几点要求：1）外部等值必须准确地描述原始系统的特性，无论内部系统运行条件如何变化，等值与未等值的网络系统的计算分析结果必须相近。2）等值方法不宜过于复杂，应具有较小的计算量，等值后的外部信息和变量尽可能少。

常用的电力系统静态等值方法有Ward等值和REI（Radial Equivalent Independent）等值法［6］，这两种方法都是属于拓扑等值。文献［8］则采用了FMC聚类方法对研究时段内具有相近特征的系统负荷状态进行分类、合并，从而构成多个等值负荷水平，减少了多元随机变量并简化了网络。除此之外还有利用系统随机变量的相关性进行简化等方法。本文提出的是运用主成分对多电源的等值分析方法，对于多台风机或风力发电场提取主成分，再结合REI等值对网络进行化简。

2 主成分分析方法

2.1 主成分分析法简介

主成分分析法的基本思想就是将多个具有相关性的变量，重新组合成相互无关的综合指标。通常数学上的处理是将原始变量进行先行组合，如果不加限制的话，这样的组合可以有很多种。要使得第一综合指标F1包含的原始信息最多，则F1的方差是所有线性组合中最大的，故称F1为第一主成分。如果第一主成分不足以代表原始变量的信息，则要选取F2，…，Fk（k＜p）多个主成分［9，10］。这样，主成分分析法将p个原始变量（X1，X2，…，Xp）转换成新的主成分F1，F2，…，Fk（k＜p）为：

要注意以下几点：

1）为了使主成分能够包含更多的原始信息，主成分的方差尽可能大。F1，F2，…，Fk所包含的信息量依次递减，则方差依次递减。所以有：

2）主成分之间互不相关，不包含重叠的信息，则

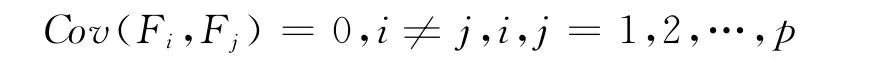
3）对于方程组的系数向量（ui1，ui2，…，uip），i＝1，…，p，是原始变量X阵的协方差矩阵∑特征值所对应的特征向量。数学上可以证明Var（F1）达到最大就是在∑第一个特征值所对应的特征向量处。每次主成分的选取使Var（F）最大，如果不加限制就会使得Var（F）→，常用每个主成分的系数平方和为1作为限制：

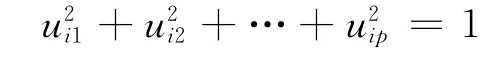
2.2 主成分的求解

1）首先将原始变量的数据进行标准化处理，来消除数据之间不同量纲等因素对计算结果的影响。

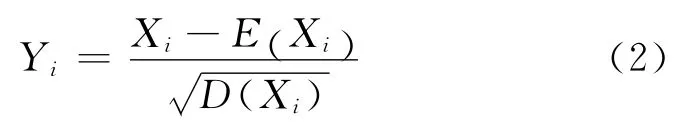
2）原始变量的协方差矩阵为标准化处理后变量的相关系数矩阵。计算p个标准化数据后的相关系数矩阵为

3）在计算出相关系数矩阵的基础之上，求得相关性系数矩阵的特征根λ（λ1，λ2，…，λp）和对应的特征向量

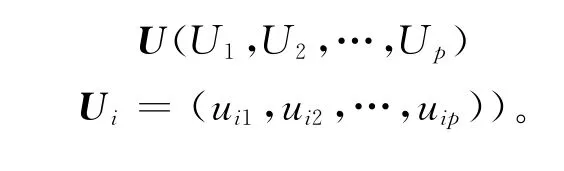
4）计算累计贡献率，求解主成分。

在求出特征根λ和特征向量U的基础上，第一主成分的系数等于第一大特征根对应的特征向量U1，第二主成分的系数等于第二大特征根对应的特征向量U，……。主成分个数的确定要通过累计贡献率的计算得到。第i个主成分的贡献率为：

累计贡献率越接近1，则说明选取的主成分包含的原始信息越多。一般而言，从第一主成分开始选取到第k主成分，使得M≥h（具体情况要求的M值可能不同，通常h取85%以上）。

根据计算出的累计贡献率对应的特征根λ1，λ2，…，λk，对应的特征向量分别为U1，U2，…，Uk（Ui＝（ui1，ui2，…，uip））。在求得主成分之前将原始数据中心化X＊i＝Xi－E（Xi），得到主成分

3 运用主成分分析法对风电场的等值

在对大规模并网风力发电场进行特性分析的时候，往往会由于风力发电机台数或者风电场过多而给分析带来过多的工作量，而在一些情况下对风力发电机的出力进行一个简单的叠加，不能很好地反映风电特性。例如在对含有多元随机变量电力系统进行概率潮流计算时，要求输入的各变量之间互不相关，但是在同一个风电场的风电出力具多种相关性，且过多随机变量会带来系统计算的复杂性。此时要对多台风力发电机的网络进行等值简化，以便于电力系统的分析和计算。

主成分分析方法对风力发电电源进行简化等值，主要可以运用到以下两个方面：

1）对于同一风电场中多台风电机组的等值 在大规模风力发电中，一个风电场往往含有数十台甚至上百台风力发电机组。在对某个风电场进行分析的时候，运用主成分分析方法提取成分，可以从较少的主成分中有效地挖掘出风电功率波动等特性。

2）主成分分析与REI等值相结合用于多个风电场的等值 在风能资源集中的区域，往往含有多个风力发电场，他们通过各自的升压变压器并入大电网。对含有风力发电机的电网进行分析时，往往会因为风电场数目过多而造成计算和分析的复杂性。对于这种情况，可以运用主成分分析与REI等值相结合的方法来对电力系统网络进行等值化简。

REI等值法是P.Dimo等人提出并应用于发达国家电力系统潮流计算与安全分析［11］。目前，REI等值广泛地运用于电力系统分析的各个领域［12－14］.其基本思想是把电网中要消去的点分为保留节点和消去节点，将需要消去的有源节点按照一定的性质分成若干组，每组用一个虚拟电源表示，图1a代表一组的情况。虚拟电源通过一个无损耗的虚拟网络（REI网络）与系统相连，图1b所示虚拟有源节点上的有功、无功注入功率是该组有源节点有功与无功功率的代数和。在接入REI网络与虚拟等价节点后，原来的有源节点就变成无源节点了，然后将所有要消去的无源节点用常规的方法消去，得到如图1c的网络［7］。

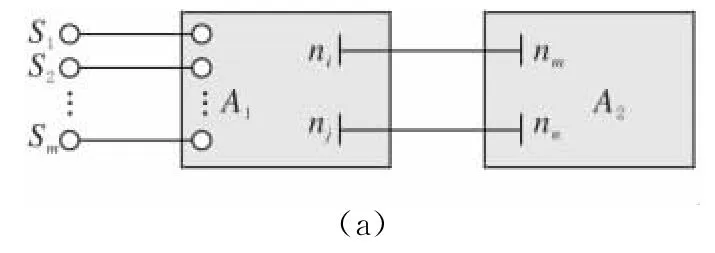
图1 REI等值网络化简

4 算例分析

算例分析中，在美国可再生能源实验室（NERL）的数据中，对于同一风电场的多台风力发电机，挑选了风力发电场编号为FJ60－FJ69的十台风电机组作为研究对象，运用SPSS软件对十台风电机组的发电功率进行主成分分析。在此，10台风机对应的时间序列的风机发电功率分别表示为X1，X2，…，X10，风电场通过这10个风机发电功率指标来描述此风电场的发电功率出力状况。对其进行主成分分析，就是要将10台风电机组功率向量指标转换成新的指标F1，F2，…，Fk（k＜10），提取出来的新的指标F1，F2，…，Fk（k＜10）表示的是代表整个风电场的k台虚拟的风电机组，这几台风电机组之间互不相关，又能够充分反映原始风电场的10台风电机组出力情况。

首先，将10台风电功率数据标准化之后求得各风电机组之间的相关系数矩阵如表1。从相关系数矩阵可以看出大部分机组间的相关系数在0.9以上，最低的相关系数为0.842，所以说各风电机组之间的相关度都很高，10台风电机组之间的风电出力特性具有一定的相似性。

表1 十台风电机组之间相关系数矩阵

通过求解相关系数矩阵的特征值，得到特征值的碎石图（图2）。每个特征值对应一个主成分，进一步得到每个特征值对应主成分的贡献率m以及累计贡献率见表2。

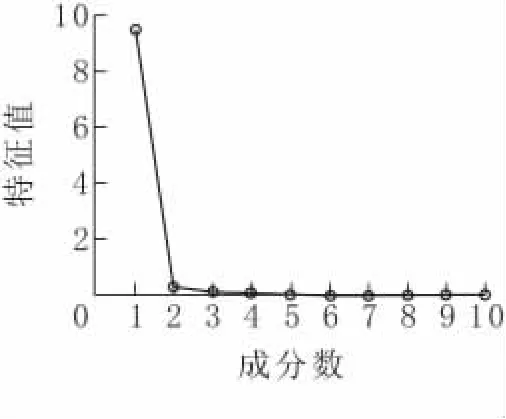
图2 特征值碎石图

表2 主成分贡献率

依据主成分的贡献率，选取第一和第二主成分，这两个主成分的累计贡献率M达到了97.46%，能够有效地提取大部分的原始信息。第一主成分和第二主成分对应的主成分系数分别为：

将10台风电机组的功率数据中心化：

那么得到此风电场发电功率第一主成分和第二主成分为：

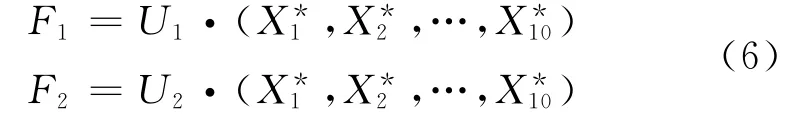
在此将10台风电机组中心化后的功率数据表示为P＊i＝X＊i，带入主成分公式得到提取出来的两个主成分为：

以上的两个主成分F1、F2表示的是代替10台风电机组的两台等效的风电机组。这两台机组能够反映原有10台机组97.46%的信息，在对这10台风电机组出力特性研究的时候可以通过对这两台等效机组的分析来实现。

主成分是原始变量的线性叠加，通过原始变量的概率模型和主成分公式可以推导出两台等效机组的概率模型以及分布参数，从而可以对虚拟风机进行深入的数据分析和风电功率的挖掘。F1、F2两台机组之间不相关，可以将两台虚拟机组的数据用于概率潮流计算等研究中，在系统分析中也可以对他们进行简单的叠加计算。

5 结论分析

主成分分析法运用较少的变量来分析问题，可以减少分析的工作量，主成分之间的不相关性减少了信息的交叉，此方法具有极高的有效性和实用性，能够对外部系统进行有效的等值。主成分网络等值法可以运用到电力系统分析的多个方面的研究，可以运用于风速的描述、对无功出力的分析负荷的等值，运用较少的主成分来替代大量的随机变量。在多风电场的系统中，运用主成分分析法与REI等值法结合可以减少系统计算分析的工作量，能够对系统进行有效地等值。

［1］ 周双喜，鲁宗相.风力发电与电力系统［M］.北京：中国电力出版社，2011：1－12.

［2］ 于 静，车俊铁，张吉月.太阳能发电技术综述［J］.世界科技研究与发展，2008，30（01）：56－59.

［3］ 高赐威，张 亮.电动汽车充电对电网影响的综述［J］.电网技术，2011，35（02）：127－131.

［4］ Denholm P，Short W.An evaluation of utility system impacts and benefits of optimally dispatched plug－in hybrid electric vehicles［R］.Colorado：National Renewable Energy Laboratory，2007.

［5］ 孙伟卿，王承民，张焰.智能电网中的柔性负荷［J］.电力需求侧管理，2012，14（03）：10－13，48.

［6］ 刘 峰.电力系统外部等值理论及实用化探讨［J］.继电器，2007，35（15）：68－71.

［7］ 诸骏伟.电力系统分析［M］.北京：中国电力出版社，1995：115－124.

［8］ 吴 蓓，张 焰，陈闽江.基于负荷模糊聚类的电压稳定概率评估［J］.电力系统自动化，2007，31（04）：23－27.

［9］ 于秀林，任雪松.多元统计分析［M］.北京：中国统计出版社，1999：162－166.

［10］黄 宁.关于主成分分析应用的思考［J］.数理统计与管理，1999，18（05）：44－46，52.

［11］Wu F F，Narasimhamurthi N.Necessary Condition for REI Re－duction to be Exact［C］.IEEE PES Winter Meeting，1979：A79065－4.

［12］邵玉槐，李肖伟，程晋生.REI等值法用于多节点配电系统短路电流计算的研究［J］.中国电机工程学报，2000，20（04）：65－68，89.

［13］刘志文，刘明波，林舜江.REI等值技术在多区域无功优化计算中的应用［J］.电工技术学报，2011，26（11）：191－200.

［14］李 智，杨洪耕.REI等值和变距线性回归在地区电网电压无功优化控制中的应用［J］.电力系统保护与控制，2012，40（01）：18－22，42.

［责任编校：张岩芳］

Studies on Wind Farm Equivalent Method Based on Principal Component Analysis

ZENG Yuan－fang，ZHANG Bu－han，WU Jun－li，BIE Pei
（State Key Laboratory of Advanced Electromagnetic Engin.and Tech.，Huazhong Univ.of Science and Tech.，Wuhan 430074，China）

Power systems Contains a large number of random power supply，load and other random variables.For the issue of system containing multiple random variables，the method of equivalent using the principal component by principal component analysis method and Combining with REI equivalent was proposed.The principal components of multi－wind farm were extracted，and the principal components were seen as the virtual equivalent wind turbines.As a result，simplified replacement was effectively implemented，and the complexity of systems analysis was reduced.

power systems；principal component analysis；simplified equivalent；wind farm；multiple random variables

TM614

A

1003－4684（2014）01－0025－04

2013－11－18

曾远方（1990－），女，湖南郴州人，华中科技科技大学硕士研究生，研究方向为电气工程及其自动化