达茂旗干旱牧区59年气候变化规律分析

徐晓民，郭中小，梁文涛

(水利部牧区水利科学研究所，内蒙古 呼和浩特 010020)

我国牧区包括内蒙、新疆、西藏、青海等12个省(区)的264个牧区半牧区县，土地总面积385 km2，占全国国土面积的40%。牧区既是边疆地区、又是少数民族聚居区，同时也是我国主要江河的发源地和水源涵养区，在全国经济发展大局中具有重要战略地位。同时，牧区草地在我国陆地生态系统中占有重要地位，具有调节气候、防风固沙、涵养水源、保持水土、净化空气以及维护生物多样性等重要生态功能，由于我国牧区大多处于内陆偏远地区，因此，降水稀少、蒸发强烈、水资源天然匮乏、自然环境恶劣、生态环境脆弱等是其自然特点。自20世纪70年代特别是80年代，在全球气候干热化趋势背景下，草原退化、沙化、荒漠化日益加剧，有些地区已经成为我国沙尘暴天气发生的主要沙源区。据统计，与20世纪80年代初相比，90%以上的可利用草原面积已呈现不同程度的退化、沙化。综合分析其产生沙退化的原因，除人类活动外，最主要的影响因子为气候变化。研究我国北方干旱牧区气候变化特征、揭示其演变规律是了解和认识草地沙退化的重要基础，具有重要的现实意义。

达茂旗位于内蒙古自治区包头市北部，北与蒙古国接壤，西与巴彦淖尔市的乌拉特中旗毗邻，南与呼和浩特市的武川县、包头市的固阳县相邻，东与乌兰察布市的四子王旗交界，地理坐标E 109°15′～111°25′、N 41°16′～42°45′，总面积18 177 km2。达茂旗地处内陆干旱地区，降水稀少、蒸发强烈、水资源天然匮乏，属于严重缺水的牧业旗之一，具有北方干旱牧区的显著特点(图1)。

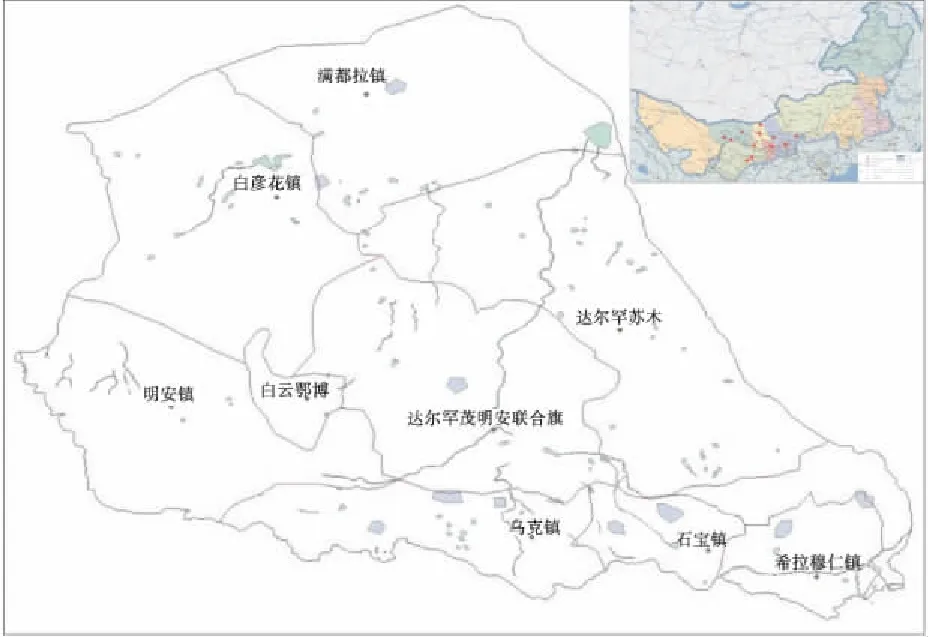
图1 研究区位置及周边气象站点图

1 资料来源与分析

1.1 资料来源

资料来源于中国气象科学数据共享服务网中国地面气候资料日值数据，选取达茂旗周边12个气象站点的气象数据进行空间插值计算，得出研究区1954～2012年月平均气温，月降水资料进行分析计算。

1.2 分析方法

作出研究区年平均气温，年降水的年变化曲线及5年滑动平均曲线图，进行数据的标准化与距平处理[1-5]。运用线性倾向估计法及回归分析法分析年平均气温、年降水的变化趋势[6-10]，应用Mann-Kendll非参数统计检验方法进行突变检验[11，12]，应用morlet复变小波分析方法研究其变化周期[13-17]。

2 气候变化趋势分析

2.1 线性倾向估计法

建立xi与ti之间的一元线性回归方程：

式中：xi表示样本量为n的某一气候变量，用ti表示xi所对应的时间。

这一方法属于时间序列分析范畴，方程中a为回归常数，b为回归系数。a和b可以用最小二乘法进行估计。

其中:b×10 a即为气候倾向率，单位为℃/10a或mm/10a。b的符号表示气候变量的趋势倾向，即b>0时，说明随时间t的增加x呈上升趋势；反之则下降。b值的大小反映了上升或下降的速率，即表示上升或下降的倾向度。

2.2 年平均气温变化趋势分析

从图2可以看出，研究区从20世纪50年代开始，年平均气温开始呈上升趋势，上升速度明显加快，年平均最低气温出现在1956年的2.1 ℃，年平均最高气温出现在2007年的6.3 ℃。从线性倾向率来看，年平均以0.41 ℃/10 a的速度上升，并通过了a=0.05的显著性检验，说明研究区年平均气温呈较强的上升趋势。

2.3 年降水变化趋势

年降水量从20世纪50年代开始，呈缓慢的减少趋势，但趋势不明显，试验没有通过显著性检验，年降水量增幅仅为-0.08 mm/(10 a)。年降水量最低为2009年，为138.4 mm，年降水量最高的是2003年，为425.2 mm(图3)。

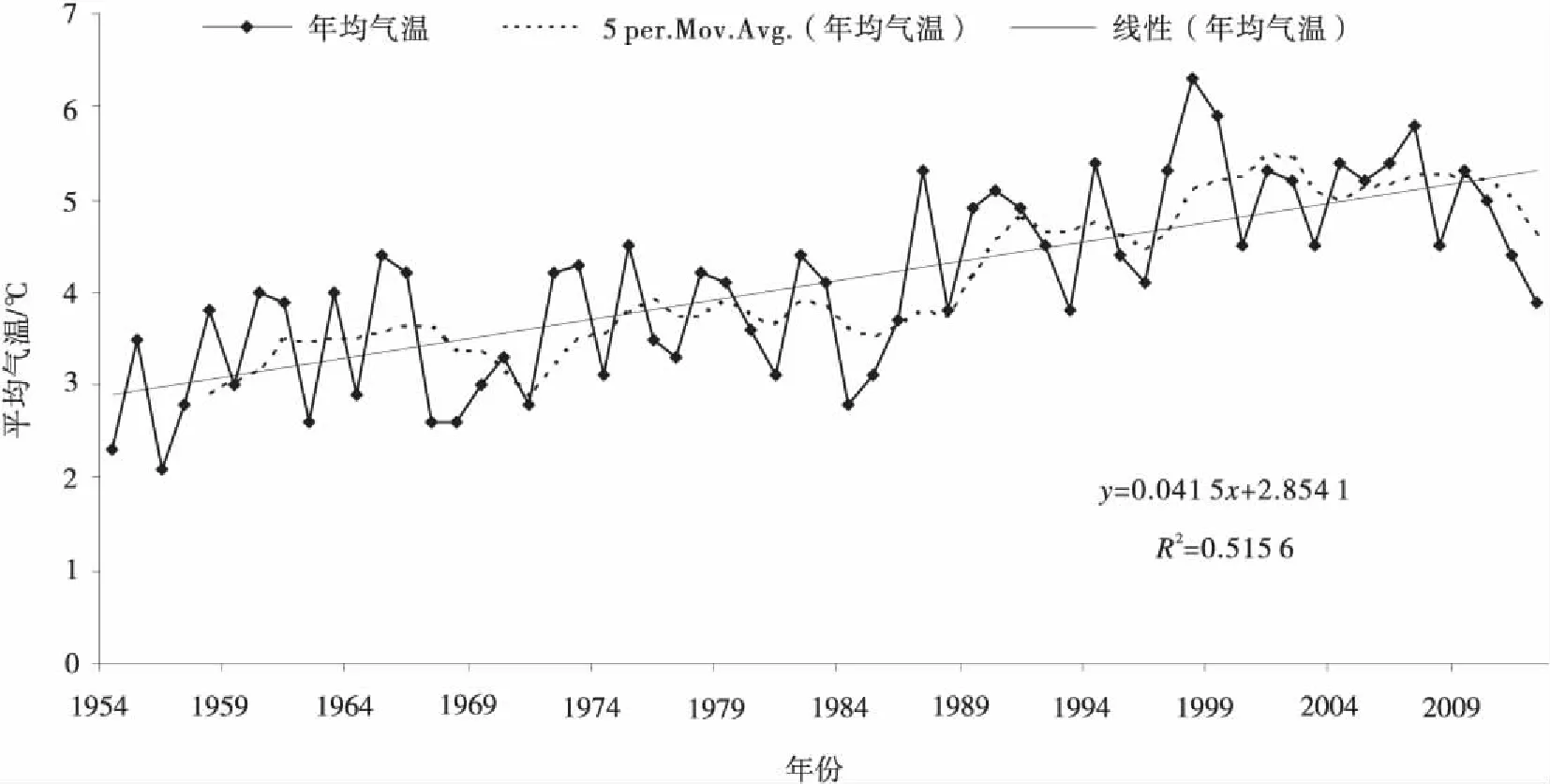
图2 研究区年平均气温变化趋势

3 Mann-Kendall突变检验

Mann-Kendall法，是一种非参数统计检验法。当Mann-Kendall检验进一步用于检验序列突变时，通过构造一秩序列：

(2)

在时间序列随机独立的假定下，定义统计量：

(3)

UFk为标准正态分布，它是按时间序列x顺序x1，x2，…,xn计算出的统计量序列，若|UFi∣>Ua,则表明序列存在明显的趋势变化。按时间序列x逆序xn，xn-1，x1，再重复上述过程，同时使UBk=-UFk(k=n，n-1，…,1),UB1=0。

3.1 研究区年平均气温M-K突变检验

由图4中的UF曲线可见，自20世纪50年代开始，年平均气温呈现了明显的上升趋势，这与线性倾向估计法的结论相一致。从1987年开始，这种增暖趋势均大大超过了显著性水平0.05的临界线，表明研究区气温的上升趋势十分显著，根据UF和UB曲线交点的位置，确定研究区年平均气温20世纪80年代的增暖是一突变现象。

3.2 研究区降水M-K突变检验

利用M-K突变检验分析研究了研究区降水量的变化趋势，通过图5可知，研究区20世纪50年代末到60年代初，70年代中期到80年代末为2个典型的降水上升期；60年代初到70年代中期为降水下降期。其他时期降水趋势不明显，降水总体趋势是小幅波动下降，并没有显著的突变，与线性倾向估计法得出的结论吻合。

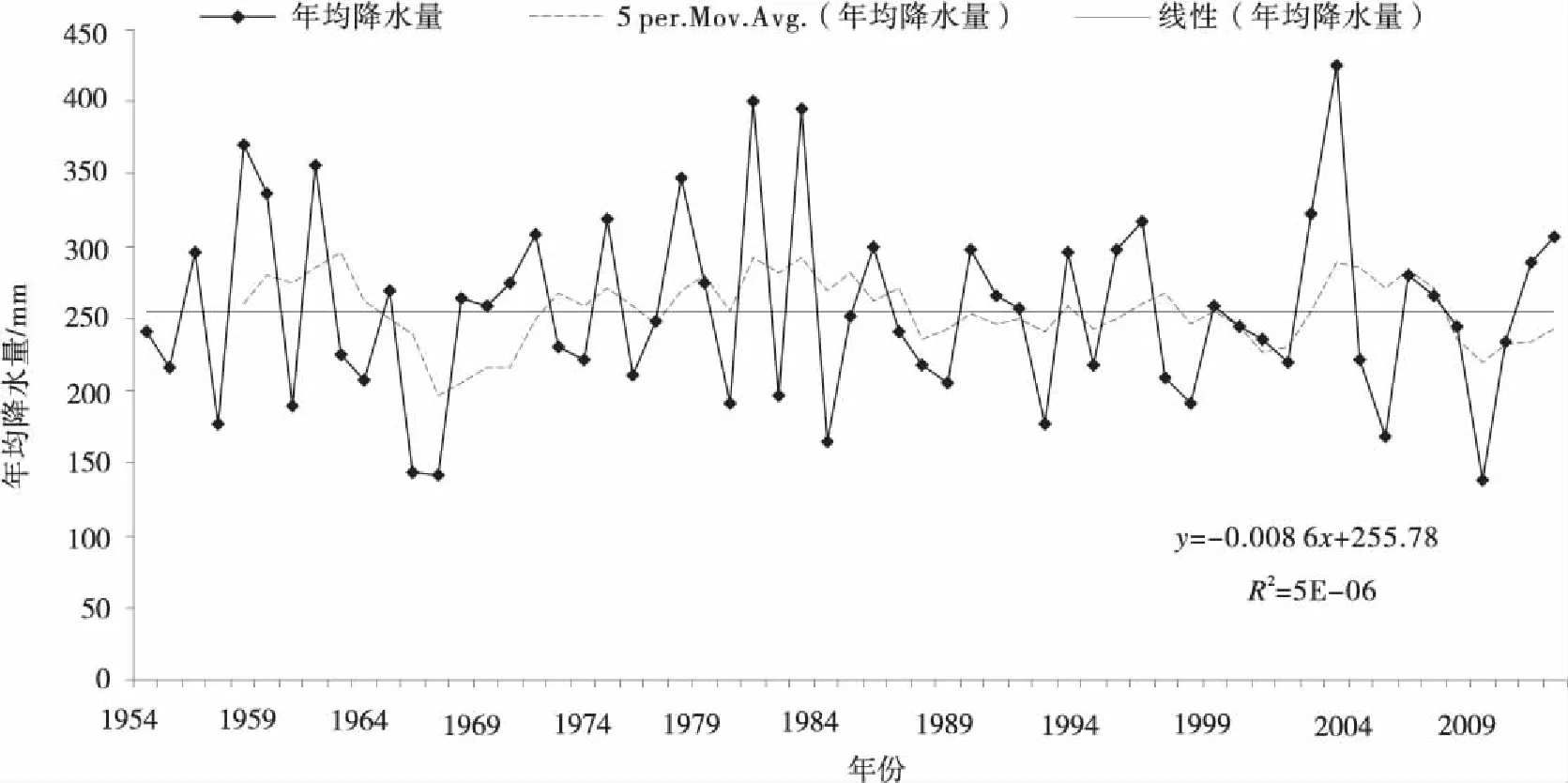
图3 研究区年降水变化趋势

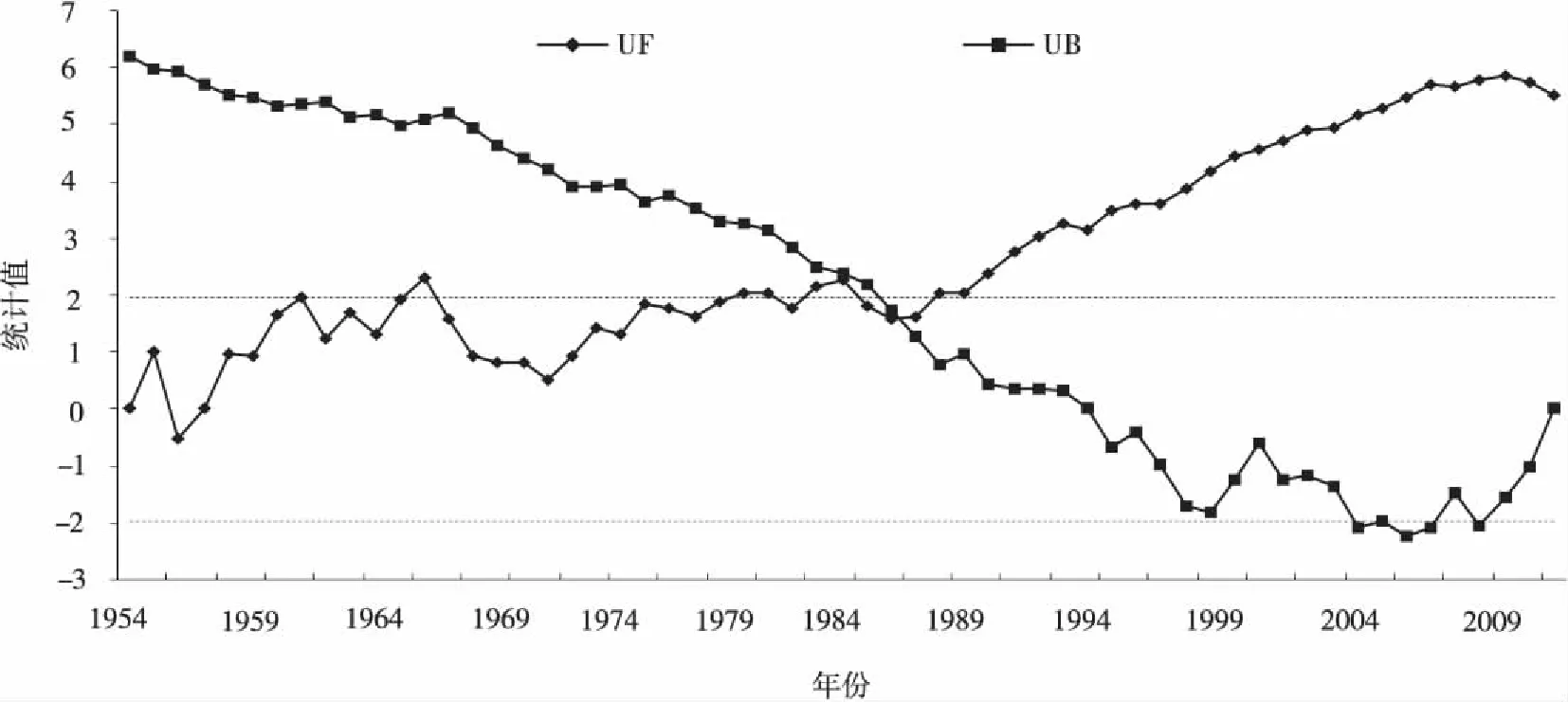
图4 研究区年平均气温M-K检验曲线

4 基于morlet复变小波的周期性分析

4.1 morlet小波变换

对于给定的小波函数ψ(t)，时间序列号f(t)∈L2(R)连续小波变换定义为：

(4)

(5)

Wf(a,b)能同时反映时域参数b和频域参数a的特性，它是时间序列f(t)或f(kΔt)通过单位脉冲响应的滤波器的输出。

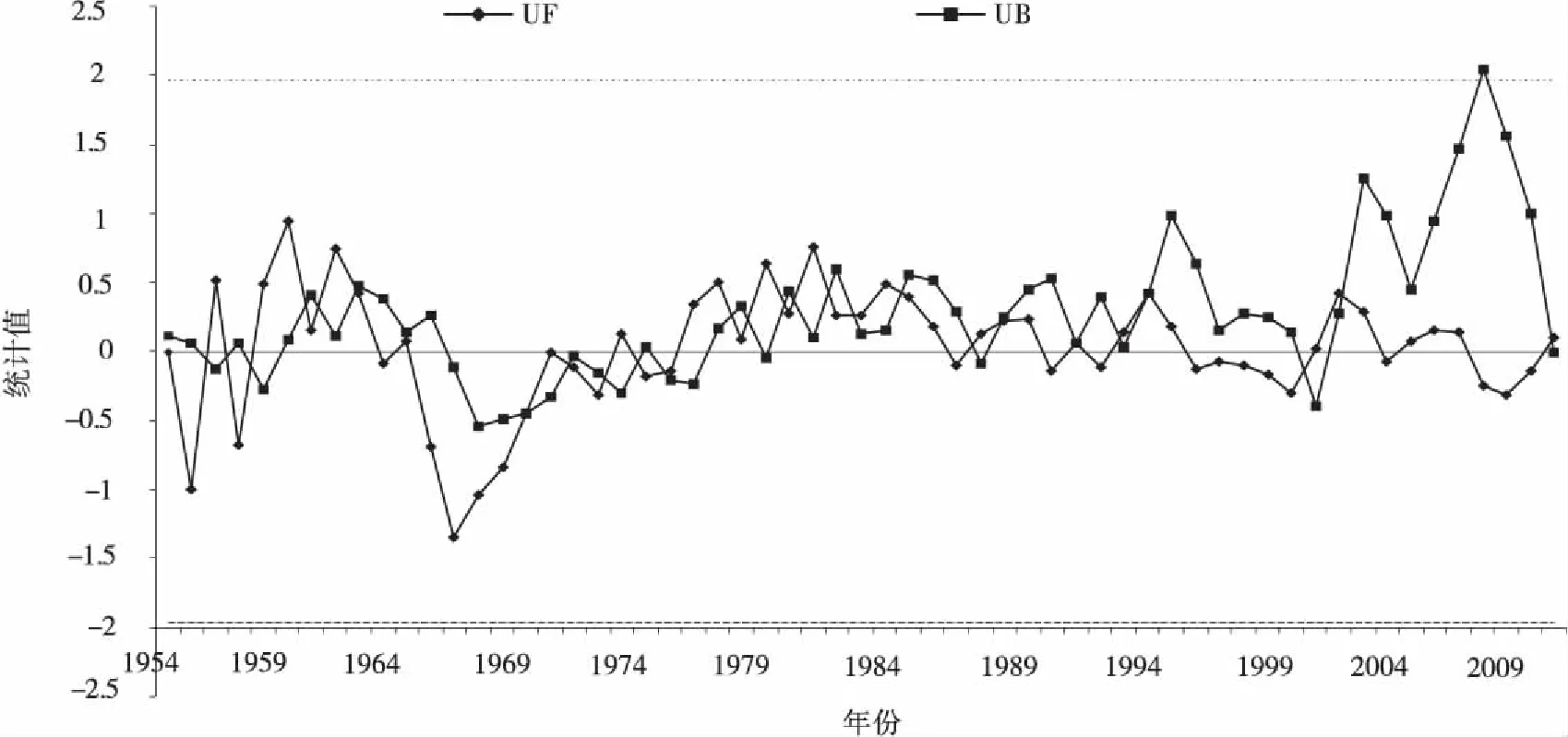
图5 研究区年降水量M-K检验曲线

4.2 小波方差

将时间域上的关于a的所有小波系数的平方在b域上积分，即为小波方差。

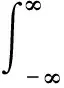
(6)

小波方差随尺度a变化过程称为小波方差图。它能反映信号波动的能量随尺度a的分布。通过小波方差图，可以确定一个水文水资源时间序列中存在的主要时间尺度，即主周期。

4.3 年平均气温周期分析

应用matlab软件绘制年平均气温小波系数实部等值线图和小波方差图。小波系数实部等值线图能反映年平均气温不同时间序列不同时间尺度的周期变化及其在时间域中的分布，进而能判断在不同的时间尺度上，年平均气温的未来变化趋势。在小波系数实部等值线图中，横坐标为时间(年份)，纵坐标为时间尺度。从图6可以看出，在年平均气温演变过程中存在着3～7a，8～16a，17～32a的3类尺度的周期变化规律。其中，在17-32a尺度上出现了高-低-高-低的两次震荡；其周期变化在整个分析时段表现的非常稳定，具有全域性。

从图7年平均气温小波方差图中可以看出，存在着3个明显的峰值，分别对应着7 a，14 a，22 a的时间尺度，其中,最大峰值对应着22 a的时间尺度，说明22 a的同期震荡最强，为年平均气温的第1主周期；14 a和7 a时间尺度分别对应着年平均气温的第2、3周期。上述3个周期的波动控制着气温在整个时间域内的变化特征。

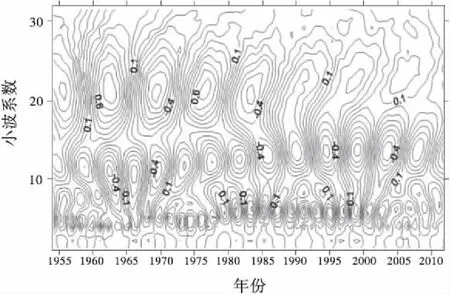
图6 年平均气温小波系数实部等值线Fig.6 The wavelet coefficient of real component contour

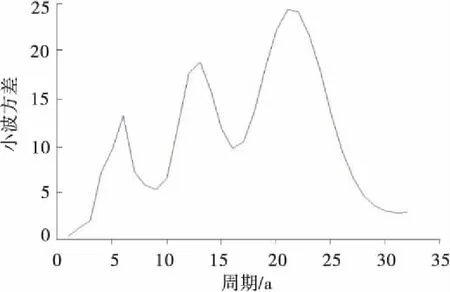
图7 年平均气温小波方差

4.4 年降水周期性分析

同样，应用matlab软件绘制年降水小波系数实部等值线图和小波方差图。从图8年降水小波系数实部等值线图可以看出，在年降水演变过程中也存在着3类时间尺度的周期变化规律，分别为3～6 a，7～9 a，12～22 a。从图9年降水小波方差图中可以看出，存在着3个明显的峰值，分别对应着4 a，8 a，18 a的时间尺度，其中最大峰值对应着18 a的时间尺度，说明18 a周期震荡最强，为年降水的第1主周期；8 a和4 a时间尺度分别对应着年降水的第2、3周期。上述3个周期的波动控制着降水在整个时间域的变化特征[18-22]。

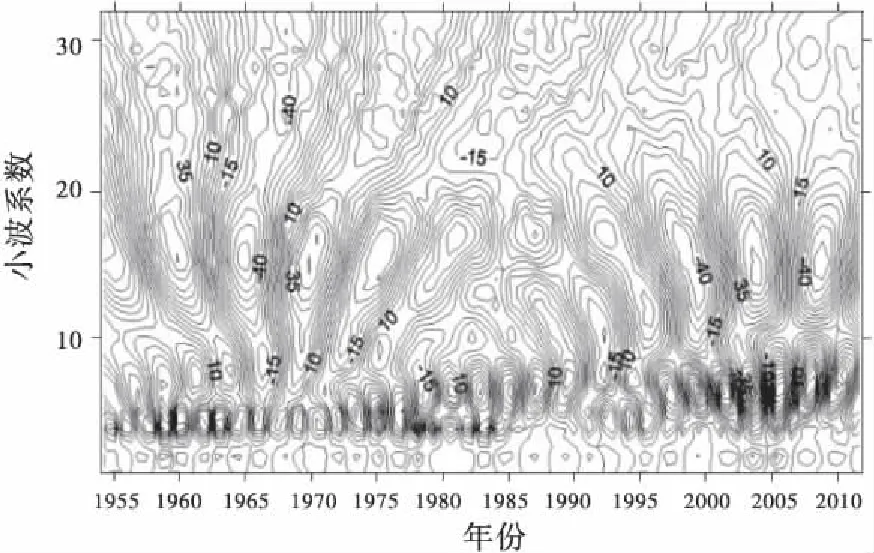
图8 年降水小波系数实部等值线Fig.8 The wavelet coefficient of real component contour

图9 年降水小波方差

5 结论

通过线性倾向率法，M-K突变检验法，morlet复变小波分析方法对我国北方典型干旱牧区达茂旗气候特征进行了分析。

(1)研究区年平均气温呈上升趋势，年均温以0.41 ℃/(10 a)的速度上升；年降水变化趋势不明显，总体趋势为缓慢下降，年增幅仅为-0.08 mm/(10 a)。

(2)经M-K突变检验，验证了研究区年平均气温的变化趋势，确定了平均气温20世纪80年代的增暖是一突变现象，具体从1986年开始。对于年降水,在20世纪50年代末到60年代初，70年代中期到80年代末为2个典型的降水上升期；60年代初到70年代中期为降水下降期。其他时期降水变化不明显。

(3)经morlet复变小波分析，在年平均气温演变过程中存在着3～7 a，8～16 a，17～32 a的3类周期变化规律。在17～32 a尺度上出现了高-低-高-低的两次震荡，在整个分析时段表现的非常稳定，具有全域性。年降水演变过程中也存在着3类尺度的周期变化规律，分别为3～6 a，7～9 a，12～22 a。18 a的周期震荡最强，为年降水的第1主周期。

参考文献:

[1] 牛赟,刘贤德,罗永忠,等.祁连山山地草地小气候特征研究[J].草原与草坪,2008(1):59-62.

[2] 张建国,孙宝利,舒海燕.辽宁省彰武县1953-2010年气候变化特征分析[J].干旱区资源与环境,2012,26(8):148-152.

[3] 王方琳,徐先英,柴成武,唐卫东.绿洲边缘固定沙丘水分时空动态变化[J].草原与草坪,2013,33(4):71-74.

[4] 魏凤英.现代气候统计诊断与预测技术[M].气象出版社,2007：36-99.

[5] Rajagopalan B,Lall R.Interannual variability in westem US precipitation[J].Journal of Hydrology,1998,210:51-67.

[6] 王艳，杨剑虹.草原沙漠化成因的探讨[J].草原与草坪,2004(107):28-32.

[7] 刘洪敏.1957～2009年辽宁省气候变化趋势分析[D].兰州：西北师范大学，2011:9-36.

[8] 陈海燕,肖天贵.安岳县近40年气候变化规律分析[J].安徽农业科学,2012,40(20):10540-10544.

[9] 王巧霞,史海平,孙悦.临汾市近48年气候变化规律研究[J].山西师范大学学报,2003,17(4):88-92.

[10] Ingram H A P.Eco-hydrology of Scottish peatlands[J].Transactions of the Royal Society of Edinburgh Earth Science,1987,78(4):287-296.

[11] 曹洁萍,迟道才.Mann-Ke nd all检验方法在降水趋势分析中的应用研究[J].农业科技与装备,2008(5):35-40

[12] 朱良燕.基于M-K法的安徽省气候变化趋势特征R/S分析及预测[D].合肥：安徽大学,2010：3-10.

[13] 韩世刚,吉莉,陈欢,等.1960～2006年重庆市高温天气频次气候特征morlet小波分析[J].安徽农业科学,2010,38(28):15732-15733.

[14] 李艳玲,畅建霞.基于Morlet小波的径流突变检测[J].西安理工大学学报,2012,28(3):322-325.

[15] Zhang Y,Shao Q,Xia J,etal．Changes of flow regimes and precipitation in Huai river basin in the last half century[J].Hydrological processes,2011,25(2):246-257.

[16] 陈群鹰,王洪波.1953～2008年合肥市气温变化特征分析[J].现代农业科技,2011(1):312-314

[17] 葛哲学,沙威.小波分析理论与MATLAB R实现[M].电子工业出版社,2007：241-274.

[18] Cannarozzo M,Noto LV,V iola F.Spatial distribution of rainfall trends in Sicity(1921-2000)[J].Physics and Chemistry of the Earth,2006,31(1):201-211.

[19] Fohrer N,Haverkamp S,Eckhardt K,etal.Hydrologic response to land use changes on the catchment scale[J].Phys Chem Earth (B),2001，26(7-8):577-582.

[20] 唐金,李霞,卢磊.1971～2009年阜康绿洲气候变化规律分析[J].干旱地区农业研究,2011,29(4):257-262.

[21] Liu C M.Analysis of balance about water supply and demand in the 21stcentury of China:Ecological water resource studying.China Water Resources,1999(10):18-20.

[22] 朱利凯,蒙吉军.中部地区近40年来降水时空变化[J].干旱区研究，2010,27(4):536-544