基于蚁群算法的油气管道预警系统优化研究
2014-09-10李明鑫王岳张月史俊杰
李明鑫,王岳,张月,史俊杰
(辽宁石油化工大学 石油与天然气工程学院,辽宁 抚顺 113001)
油气管道应急系统对于管道安全稳定运行至关重要,而管道预警系统又是应急系统的一个重要环节[1-2]。
随着仿生学和计算技术的不断发展,形成了一系列智能优化方法。目前应用较广的主要有遗传算法、神经网络、微粒群算法、蚁群算法等,其中蚁群算法是一种新型的群智能理论模拟算法[3-4],虽然该方法的研究时间不长, 但现有的研究表明: 蚁群算法在求解复杂动态规划问题,特别是离散型规划问题方面具有一定的优势,是今后极具发展前景的优化算法。笔者系统分析了油气管道预警系统的结构,并借助蚁群算法,得到预警系统各设备故障概率,在专项经费一定的情况下,对系统安装并联备用设备进行优化研究,实现整个系统的可靠性最大化。
1 蚁群算法基本原理
蚁群算法(Ant Colony Optimization)又称蚂蚁算法,是一种用来在图中寻找优化路径的几率型算法。其灵感来源于蚂蚁在寻找食物过程中发现路径的行为,即观察真实蚂蚁的行为,建立起相应的行为模型,然后将这些模型用于设计新的算法,以解决优化问题、离散控制以及聚类等相应的问题。蚁群算法在解决组合优化问题中取得了一系列较好的实验结果,因而该算法逐渐引起了研究者的注意,并将其应用到实际工程问题中[5]。如蚁群算法在解决 TSP、指派以及车间调度等离散领域优化问题有着自身的优势,并取得了很大的进展与收获[6]。
1.1 蚁群算法数学模型概述
设τi j(t)为t时刻路径(i,j)上的信息素浓度,bi(t)为t时刻位于城市i的蚂蚁数目,m为蚁群中蚂蚁的总数目,即m=∑bi(t),n为TSP规模,即城市的数目。初始时刻各条路径上信息素浓度相等,设τi j(t)=const为常量。

(1)
式中: allowedk——蚂蚁k下一步选择的城市;α——信息启发式因子,表示轨迹的相对重要性,反映了蚂蚁在运动过程中所积累的信息在蚂蚁运动时所起的作用,其值越大,则该蚂蚁越倾向于选择其他蚂蚁经过的路径,蚂蚁之间的协作性越强;β——期望启发式因子,表示能见度的相对重要性,反映了蚂蚁在运动过程中启发信息在蚂蚁选择路径时受重视的程度,其值越大,则该状态转移概率越接近于贪心规则;ηi k(t)——与路径(i,j)相关联的启发式信息值。对于TSP,其表达式如下:
(2)

为了避免残留信息素过多引起残留信息淹没启发信息,在每只蚂蚁走完1步或者完成对所有n个城市的遍历(也即1个循环结束)后,要对残留信息进行更新处理,由此t+n时刻在路径(i,j)上的信息素可按照如下规则进行调整:
τi j(t+n)=(1-ρ)τi j(t)+Δτi j(t)
(3)
(4)
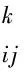
1.2 预警系统故障诊断
任何设备在发生状况时,其输入或输出信号将表现出与正常运行不同的特征,因而故障识别可转化为对设备运行状态特征聚类的问题[7]。设
F={Fi|Fi=(fi1,fi2,…,fi n),i=1, 2,…,N}
(5)
式中:F——待进行分类的数据特征;n——数据特征个数;N——数据总数。
1) 将N个数据各自聚为一类,即: (C1,C2, …,CN)。
2) 类Ci,Cj之间的距离按式(6)计算:
(6)
式中:di j——欧式空间距离;Ci,Cj——类i,j的中心向量;Ni,Nj——类i,j中数据总量。
3) 信息素浓度计算: 设r为聚类半径,τi j(t)为t时刻路径(i,j)上的信息素浓度,即:
(7)
4) 计算归并概率。当di j≤r时,若类i,j的属性k的距离d(i,j,k) ≤ra(k)时(注:ra(k)为k类属性的最小距离),直接归并,否则计算归并概率[8]:
(8)
式中:S——到第j类距离小于等于r的所有类的集合,S={s|di j≤r,s=1, 2, …,j-1,j+1, …,M},其中,s代表某一类号,M为当前总的类的数目。
5) 判断初始给定的概率阈值,并按照式(3)~(4)计算聚类中心t到t+1时刻,有q只蚂蚁选择路径(i,j)时的信息素变化量及信息素挥发率。
6) 判断是否归并,若无归并,停止循环,否则继续执行式(6),这样就可以得到每个设备发生故障的次数。
1.3 预警系统可靠性优化研究
由1.2节可计算出预警系统各设备故障概率,现要求在专项经费一定的情况下,对系统安装并联备用设备,使整个系统可靠性最大,此类问题可归结为典型的背包问题[9-10]。这里仍采用蚁群算法对设备购置进行最优决策。
分析可知: 该问题在数学上可归动态规划问题,假设要购买m类n台备用设备(m
(9)
(10)
si-1=si-ci
式中:xi——第i阶段购买的设备数;si——第i阶段的可用资金。
2 算例仿真及结论
以某长输管道预警系统为例,整个系统由近端适配器A、主控仪器B和终端管理器C二部分组成,如图1所示。任一设备发生故障,均会使整个系统受到严重影响,现决定对每台设备配置并联备用设备,以增加其可靠性。每台设备单价分别为2,3,1万元,可用专项经费10万元,在根据统计资料进行预警系统故障排查时,选取信息素的挥发率为0.7,蚁群数为10,迭代100次;在计算最优设备配置决策时,选择信息素的挥发率为0.5,蚁群数为10,迭代100次,计算结果见表1所列。
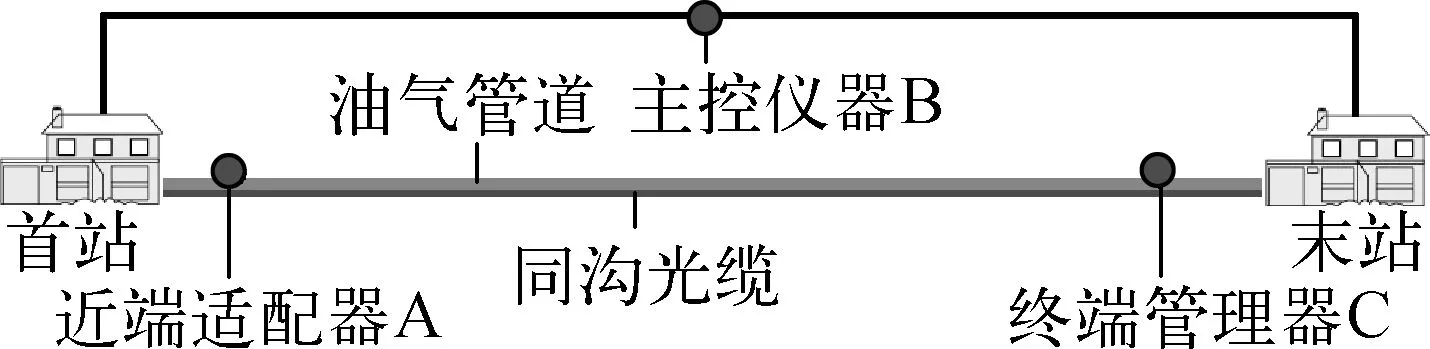
图1 油气管道预警系统示意
表1给出了油气管线预警系统设备优化结果,可以看出,终端管理器的故障率相对最大,近端适配器次之,主控仪器最小;在专项经费一定的情况下,购买2台设备A,1台设备B,3台设备C为最优购买决策,此时系统的可靠性概率为0.682,采用蚁群算法优化预警系统是可行的。
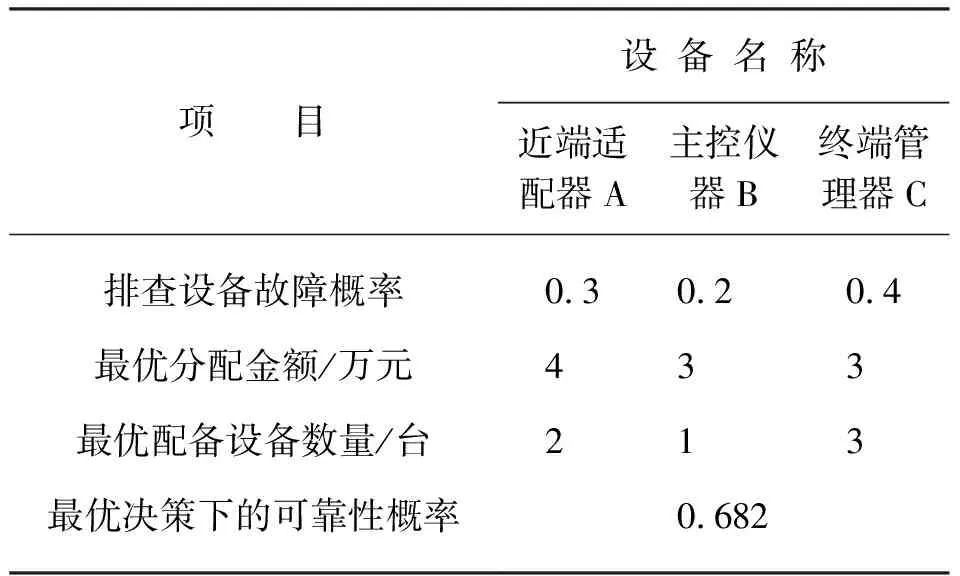
表1 计算的最优结果
3 结束语
1) 蚁群算法对优化问题的数学模型没有具体要求,只要是能够显式表达,就能够正确求解。所以,应用蚁群算法求解油气管道预警系统各设备故障概率,计算速度快,且易于实现。
2) 针对油气管道预警系统的优化问题,结合算例仿真计算和分析表明,在专项经费一定的前提下,通过计算设备故障率来选取最优设备配置决策,能够达到投资最小化,同时实现整个系统的可靠性最大化。
参考文献:
[1] 朱小华,杨骏.天然气长输管道应急救援系统开发研究[J].天然气与石油,2009,27(02): 38-41.
[2] 董先聚.管道燃气企业的危机管理[J].煤气与热力,2009,29(10): 34-35.
[3] 陈建军. 蚁群算法在物流配送路径优化中的研究[J].计算机仿真,2011,28(02): 268-271.
[4] 张颖,周韧,钟凯.改进蚁群算法在复杂配电网故障区段定位中的应用[J].电网计算,2011,35(01): 224-228.
[5] 毋玉芝,周超.蚁群算法及其在求解优化问题中的应用[J].科技信息,2007(31): 9,69.
[6] DORIGO M,MANIEZZO V, COLORNI A.Ant System: Optimization by a Colony of Cooperating Agents[J].IEEE Transactions on Systems, Man, and Cybernetics-Part B, 1996, 26(01): 29-41
[7] 白士红,唐辉辉. 蚁群算法在故障诊断中的应用[J].中国工程机械学报,2010,8(04): 466-469.
[8] 杨淑莹.模式识别与智能计算[M].北京: 电子工业出版社,2008.
[9] 刘华蓥,林玉娥,刘金月.基于蚁群算法求解 0/1背包问题[J].大庆石油学院学报,2005,29(03): 59-62.
[10] 胡小兵,黄席樾.基于蚁群优化算法的0-1背包问题求解[J].系统工程学报,2005,25(05): 520-528.
[11] 宋士祥,张强,吴明,等.基于GIS和SOA的长输管道管理系统的设计与实现[J].化工自动化及仪表,2012,39(08): 998-1000,1033.
