植入式传感器系统中无线电能发射线圈的研究

江 虹，朱小宁

(长春工业大学电气与电子工程学院，长春130012)

植入式传感器系统中无线电能发射线圈的研究

江 虹，朱小宁

(长春工业大学电气与电子工程学院，长春130012)

为提高磁共振式无线电能传输系统的工作效率，提出研究磁通量接收线圈强度的方法。以发射线圈为研究对象，通过一种形函数对圆形、矩形线圈进行仿真计算和深入研究。在实际效果区别较大的线圈形状中，找出最优的线圈设计方法，使其可在植入式传感器领域更好地应用。研究结果表明，选取矩形发射线圈可同时在4个内角为4个接收装置供能，从而大大提高传输效率。

植入式;无线电能传输;形函数

0 引言

磁共振式无线电能传输技术在2007年被提出后［1］，人们努力开发其民用领域，但至今没有得到广泛应用。笔者研究其在植入式传感器中应用的同时，努力改进、提高电能传输的效率和距离，并着重研究接收和发射线圈的设计［2］。以往的磁共振式无线电能传输通常使用相同尺寸的发射线圈和接收线圈，但这种方式并不适用于医疗领域的植入式传感器［3］。鉴于其工作环境，植入端设备的接收线圈尺寸受到严格限制，所以研究发射端线圈产生的磁场分布尤为重要。

笔者通过一种经过Fourier变换的Biot-savart法则所得到的形函数［4］，分别对形状为圆形、矩形的通电线圈产生的磁感应强度建立数学模型并仿真。通过对仿真结果的分析，在本质上认识到磁共振式无线电能传输系统中发射线圈选取的重要性。

1 平面内任意形状的闭合通电线圈产生的磁场强度

如图1所示，建立空间直角坐标系。将一个任意形状的单匝闭合通电线圈放置在z=z0处，通电电流为I(x，y)逆时针方向。将这个闭合线圈微分成无限多个节点［5］，则第i段节点(即xi-1到xi)所带电流为fi(x)，如图2所示。

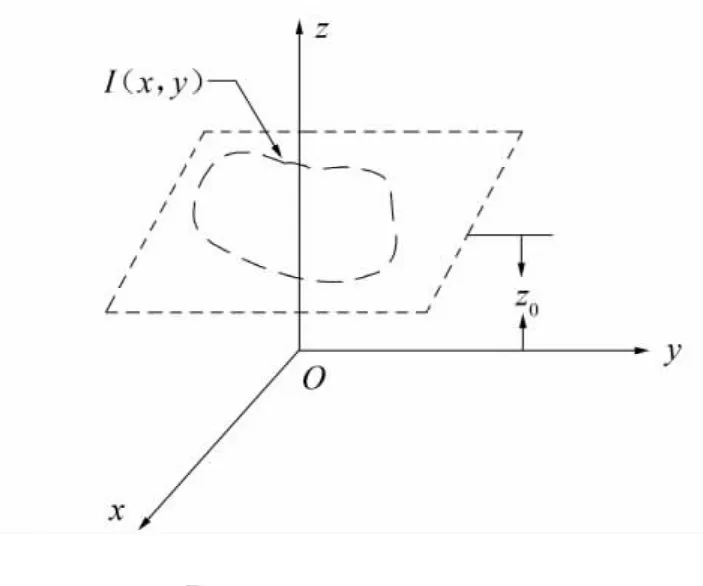
图1 平面内的任意形状线圈Fig.1 Arbitrary shaped planar coil in space

图2 分割的闭合环形电流Fig.2 Small closed loop current

由Biot-savart法则平面内任意形状通电闭合线圈所形成的磁感应强度在 x、y、z轴方向的分量为［6］

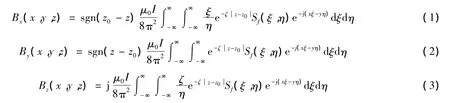
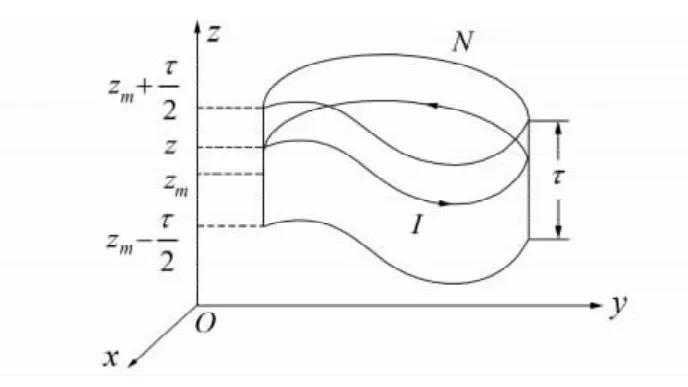
图3 N匝任意形状线圈Fig.3 Single-layer arbitrary shaped coil

最后只需分别把圆形、矩形的形函数带入式(4)～式(6)即可得到对应形状、匝数的线圈通电后形成的磁感应强度分布。

2 仿 真

2.1 圆形线圈

假设圆形线圈所在平面为xy平面，当接收线圈与发射线圈平行时是最大传输效率的角度［8］，即磁场在z轴方向的场强对传输效率有直接影响。

圆形线圈形函数为

通过Matlab对两种线圈形成的磁感应强度绘制仿真图［9］(见图4)。其中匝数为20，半径为10 cm，每匝电流为5 A，且流向相同，观测点范围在线圈内部。

2.2 矩形线圈

同样地，设矩形线圈所在平面为xy平面。矩形的形函数为

得到

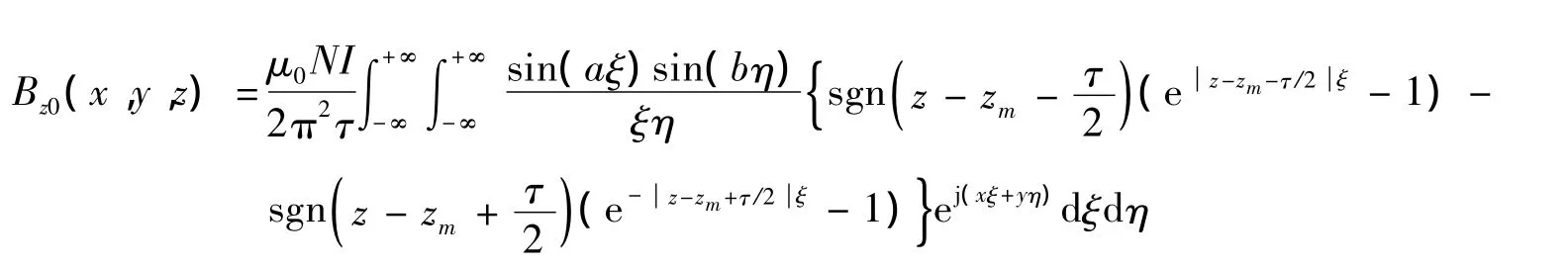
在不改变线圈最大半径的情况下，同样为20匝、边长为20 cm、每匝5 A的通电矩形线圈Matlab仿真图如图5所示。

图4 圆形发射线圈形成磁场的二维图Fig.4 2D-map of the magnetic field created by circle coil

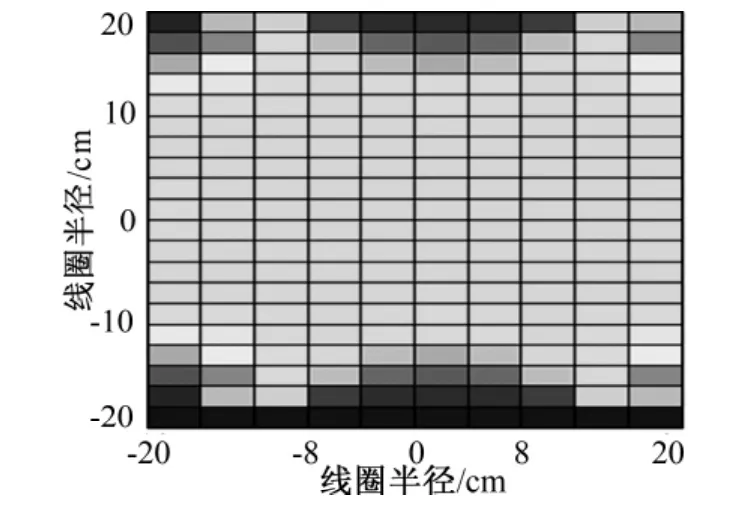
图5 矩形线圈形成的磁场二维图Fig.5 2D-map of the magnetic field created by rectangular coil

3 仿真结果分析

当只考虑磁场在z轴方向的分力，绘制出平面二维图，颜色越深表示磁场延z轴方向的分力越大。可以看出，圆形线圈和矩形线圈都具有各自特点，圆形线圈磁感应强度分布均匀，但局部场强不高;矩形线圈在4个内角的磁感应强度很高，但线圈内部场强分布较复杂。

当把x、y、z轴的磁感应强度分量积分累加，用Matlab绘制出通电矩形线圈形成磁场强度的三维图形(见图6)，可更加直观地看出4个内角的磁感应强度明显高出中心位置，x、y轴表示矩形线圈所在平面。图6b为磁场在yz平面的透视图，z轴单位均为10-7A/M。

利用上述特点，在磁共振式无线电能传输系统下的植入式传感器供能装置中。发射线圈的设计可采用较大尺寸的矩形线圈，接收端线圈可以采用较小尺寸的圆形线圈(因为最大半径相同时，圆形面积最大)，这样可高效地进行电能传输。而且在今后的研究中可将重点转向一个电能发射设备为多个接收设备供能的情况，相同尺寸线圈理论上也可以一对多地传输电能［10］，但在实际应用中情况更复杂。而笔者提出的大尺寸矩形线圈，在4个内角为4个接收设备供能的情况更符合实际应用。

图6 矩形线圈形成磁场的Matlab仿真图Fig.6 Matlab simulation of the magnetic field created by rectangular coil

4 结语

笔者利用一种经过Fourier变换的Biot-savart法则所得到的形函数，对通电后的圆形、矩形线圈建立数学模型，并进一步仿真出磁感应强度分布图。

通过仿真图直观地认识到在磁共振式无线电能传输系统中，发射线圈在设计形状时有本质区别。特别应用到植入式传感器领域时，矩形线圈在4个内角的磁感应强度可以更高效地为接收线圈较小的电能接收设备供能。而矩形线圈磁场强度分布较为复杂，需要进一步研究才能确定使场强分布不均匀的因素，从而稳定矩形线圈输出的磁场［11］，可更好地为植入式传感器供能。

［1］KURS A，KARALIS R，MOFFATT J D，et al.Wireless Power Transfer via Strongly Coupled Magnetic Resonances［J］.Science，2007，317:83-86.

［2］ZHU Wei，FANG Wenzhu，ZHAN Shanshan.Volume Conduction Energy Transfer for Implantable Devices［J］.The Journal of Biomedical Research，2013(6):509-514.

［3］范兴明，莫小勇，张鑫.磁耦合谐振无线电能传输的研究现状及应用［J］.电工技术学报，2013(12):75-82.FAN Xingming，MO Xiaoyong，ZHANG Xin.Present Study and Application of Strongly Coupled Magnetic Resonances［J］.Transactions of China Electrotechnical Society，2013(12):75-82.

［4］江俊勤.亥姆霍兹线圈磁场均匀性的研究［J］.广东教育学院学报，2006，26(5):61-66.JIANG Junqin.Study on Uniform Distribution of the Helmholtz Coil Magnetic Field［J］.Journal of Guangdong Education Institute，2006，26(5):61-66.

［5］张三慧.大学物理［M］.北京:清华大学出版社，2009.ZHANG Sanhui.University Physics［M］.Beijing:Tsinghua University Press，2009.

［6］DODD C V，DEEDS W E.Analytical Solutions to Eddy-Current Probe Coil Problems［J］.Journal of Applied Physics，1968，39:2829-2838.

［7］BOYS J T，GREEN A W.Inductively Coupled Power Transmission Concept-Design and Application［J］.The Institution of Professional Engineers New Zealand Transmissions，1995，22(1):1-9.

［8］雷银照.轴对称线圈磁场计算［M］.北京:中国计量出版社，1991.LEI Yinzhao.Ax Symmetric Coil Magnetic Field Analysis［M］.Beijing:China Metrology Press，1991.

［9］ZHANG Fei，STEVEN A.Wireless Energy Transfer Platform for Medical Sensors and Implantable Devices［C］//31st Annual International Conference of the IEEE EMBS Minneapolis，Minnesota，USA:IEEE，2009:1045-1048.

［10］BENFORD J.Space Applications of High-Power Microwaves［J］.IEEE Transactions on Plasma Science，2008，36(3):569-581.

［11］ZHANG F，HACKWORTH S A.The Relay Effect on Wireless Power Transfer Using Witricity［C］//14th Biennial IEEE Conference on Eletromagnetic Field Computation.Chicago Illinois，USA:［s.n.］，2010:9-12.

(责任编辑:刘东亮)

Research on Wireless Energy Transfer Platform for Implantable Devices

JIANG Hong，ZHU Xiaoning
(School of Electrical and Electronic Engineering，Changchun University of Technology，Changchun 130012，China)

To improve the efficiency of the energy transmission system，a method that can obtain the density gone through the receiving coil，will mainly used in study on the magnetic field that created by the transmitting coil，and stimulate the field with a sort of shape function is proposed.Because of using rectangle and circle as the transmitting coil differentiate the effect of transmission efficiency，we need to find out the optimal shape of the transmitting coil.The results say that rectangular transmitting coil can provide energy for four devices simultaneous，and more effective than circle coil.

implantable device;wireless energy transfer;shape function

TM835

A

1671-5896(2014)02-0177-04

2013-09-27

吉林省科技发展计划工业高新技术研究类基金资助项目(20140204007GX)

江虹(1970— )，女，长春人，长春工业大学副教授，硕士生导师，主要从事智能仪器、图像处理和测试计量技术及仪器研究，(Tel)86-13514307926(E-mail)jianghong@mail.ccut.edu.cn。