空间机器人的SVM 非线性补偿滑模控制研究

邓玉龙，王从庆

(南京航空航天大学自动化学院，南京210016)

空间机器人的SVM 非线性补偿滑模控制研究

邓玉龙，王从庆

(南京航空航天大学自动化学院，南京210016)

为提高机械臂末端跟踪目标轨迹速度，提出了一种基于SVM(Support Vector Machine)非线性模型估计的滑模控制方法。该方法通过SVM对参数不确定非线性项进行估计，对空间机器人动力学模型进行补偿。这种从整个闭环系统稳定性出发设计的SVM非线性补偿滑模控制器，不需要确切的数学模型，从而提高了快速跟踪目标轨迹，减小跟踪误差的动力学系统性能。仿真结果验证了该控制方法的有效性、可行性。

空间机器人;支持向量机;非线性估计;滑模控制

0 引言

由于工作性质的特殊性，空间机器人处于失重状态，其质量随着时间变化，空间机器人在操作过程中载体位置和姿态均不受控制。此外，空间机器人的动力学模型非常复杂，并存在各种不确定性，如质量、惯性矩阵及负载等，难以获得精确的动力学模型，且外部扰动信号也会对控制产生一定影响。总之，空间机器人系统是一个高度耦合的非线性系统。

对空间机器人的动力学建模及其控制方法，人们已经在多方面进行了研究。文献［1］提出了一种自适应控制方法，在设计过程中需要对动力学方程进行参数线性化，并进行繁复的前期计算以确定回归矩阵。对未知参数的准确估计，决定了自适应控制能否成功实现控制目标。文献［2］利用神经网络实现模糊推理，使模糊控制具有自学习能力，提出了基于模糊神经网络的空间机械臂自学习控制策略，但该方法不能确保系统的稳定性。文献［3，4］提出了一种智能控制方法，不要求知道控制对象的精确模型，但该方法需要过多的调整参数，占用较多的计算时间，不利于系统的实时性。针对不确定性系统，文献［5-8］分别介绍了基于神经网络的模型不确定性非线性函数逼近补偿控制方法，该方法能较好地逼近目标非线性函数，但神经网络权值的调整需要消耗较多的计算时间，因而降低了逼近速度。

笔者针对空间机器人非线性系统的轨迹跟踪，提出了一种基于SVM(Support Vector Machine)非线性估计的滑模控制方法。与基于神经网络的估计方法相比，基于SVM方法节省了权值调整时间。该方法经采集样本数据训练SVM，对空间机器人动力学不确定非线性模型估计并补偿。这种控制策略不需要确切的数学模型，取得了提高轨迹跟踪速度和缩小跟踪误差的动力学系统性能。基于Lyapunov理论证明了闭环系统的稳定性，并对一个3自由度的自由浮动空间机械臂在平面内的运动进行了仿真验证。

1 自由浮动空间机器人动力学方程

笔者讨论的是一个自由浮动平面3关节空间机械臂(见图1)。该机械臂系统由航天器基座和机械臂组成。基座半径为Lb，各连杆长度分别为L1，L2，L3，连杆附体坐标系由Denavit-Hartenberg方法建立。图1中，Σ0-O0X0Y0为惯性坐标系;Σb-ObXbYb为固定于基座质心的基座坐标系;Σi-OiXiYi(i=1，2，3)为固定于机械臂第i关节的附体坐标系;Σc-OcXcYc为固定于机械臂末端质心的坐标系;θi为各关节转角;rb，ri，rc分别为惯性坐标系原点到本体坐标原点、各连杆质心和机械手坐标系原点的位置矢量。

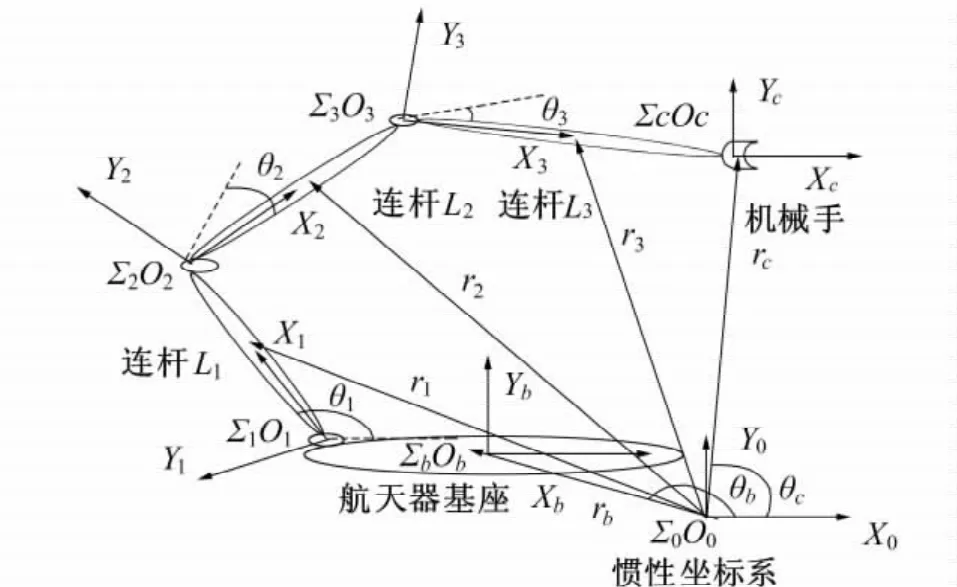
图1 空间机器人系统结构Fig.1 Space robot system structure

图1所示的3关节空间刚性机械臂，考虑摩擦力，其动力学方程可表示为［9］

其中θ=［θ1，θ2，θ3］T∈R3×1，，分别表示关节转角的位置、速度和加速度;M(θ)∈R3×3为对称正定的惯性矩阵;V(θ，)∈R3×3为科氏力和向心力矩阵;F()∈R3×1为摩擦力矢量;G(θ)∈R3×1为重力矢量，太空中机械臂为失重状态，可以忽略重力的影响;τ∈R3×1为控制转矩输入矢量。

关节矢量 θ 与末端位置矢量 Xc=［Xcx，Xcy，θc］T∈R3×1存在如下关系

其中J∈R3×3为关节空间到机械臂末端位置空间的广义雅可比矩阵［10］。将式(2)代入式(1)，得

2 基于SVM非线性补偿的滑模控制器

考虑自由浮动空间机械臂系统动力学方程(3)。为减少机械臂动力学建模参数不确定非线性对系统控制的影响，加快学习速度，实现自由浮动机械臂末端轨迹跟踪的目的，提出基于SVM不确定非线性补偿的滑模控制方法(见图2)。

图2 基于SVM不确定性补偿滑模控制框图Fig.2 SVM uncertainty compensation sliding model control block diagram

采用快速终端滑模控制实现机械臂末端的轨迹跟踪控制，即在滑动模态超平面的设计中引入非线性函数，使滑模面上的跟踪误差在有限时间内收敛到零。

由式(3)得

式(4)整理后得

取控制律

对式(7)求导可得

将式(6)代入式(8)，得

定理 控制律(6)可保证系统从任意初始状态收敛到滑模面。

证明 选取Lyapunov函数

对式(10)求导得

由式(11)得出，只要取正定对角常数矩阵Kv≥F，则有≤0，使系统趋于稳定。即选取适当的设计参数，可使控制律(6)有效控制机械臂末端跟踪期望轨迹。

3 支持向量机

SVM回归的基本思想是通过一个非线性映射Φ(·)，将数据x映射到高维特征空间，并在这个空间进行线性回归。一般的回归问题可以表述为:给定w个训练样本，学习机从中学习输入、输出变量之间的关系。假设给定了训练数据{(xi，yi)，i=1，2，…，w}，其中xi∈Rn是第i个学习样本点的n维输入值，yi∈R为对应的目标值，w为训练样本数目。目标就是寻找一个函数f(x)使其能较好地逼近所有的样本点［11］。总体上，SVM的估计函数表示如下

在变换的高维特征空间中，最优目标函数将使如下损失函数最小

约束条件为

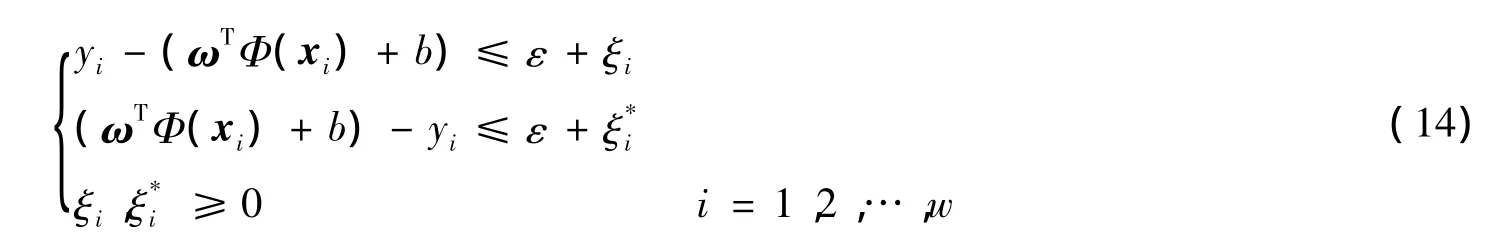
式(13)在约束条件下的最优问题，可用拉格朗日泛函引导的对偶优化问题表示为

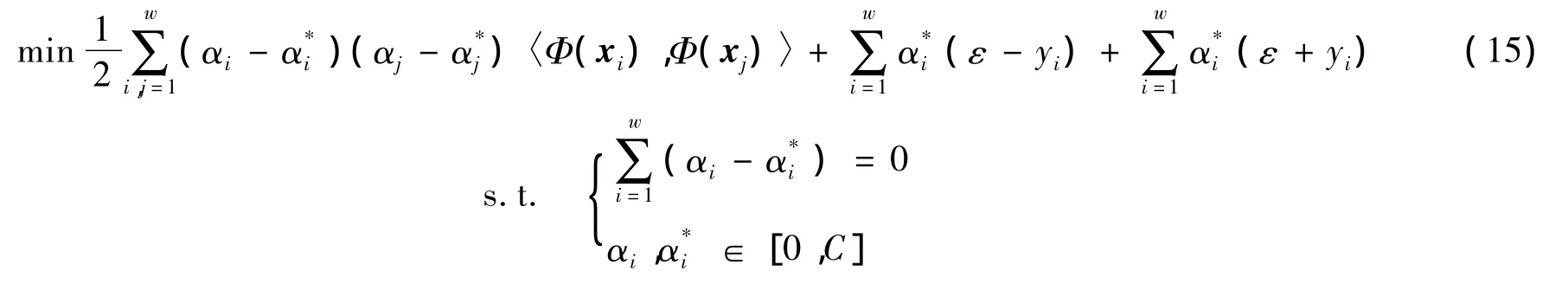
此时，非线性函数Φ(·)未知，特征空间的维数很高，因此ω*无法显示地表达。SVM算法的特殊效果在于引入核函数技巧，使函数回归绕过特征空间，直接在输入空间上求取，从而避免了计算非线性映射Φ(·)。

设核函数k(x，x*)满足

最终可得

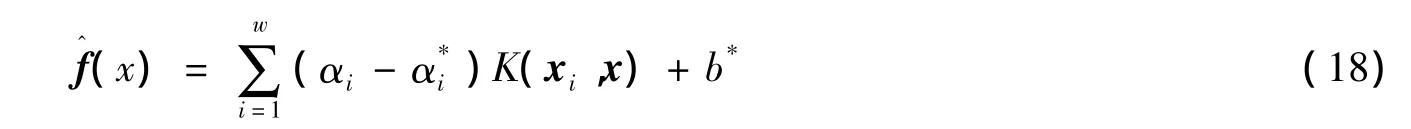
此即为支持向量回归机。

概括地说，SVM通过用内积函数定义的非线性变换，将输入空间变换到高维空间，利用输入样本对SVM训练实现对空间机械臂的非线性函数逼近，进而以较小的逼近误差对系统的非线性部分进行补偿，提高系统的动态性能。

4 仿真算例及分析

以自由浮动三连杆空间机器人为仿真模型，验证所提出的控制方案的有效性。系统仿真参数如下。

本体:mb=2 000 kg， lb=2 m， Ib=1 000 kg·m2。

连杆 L1:m1=4 kg， l1=2.2 m， I1=2 kg·m2。

连杆 L2:m2=4 kg， l2=2.2 m， I2=2 kg·m2。

连杆 L3:m3=4 kg， l3=2.2 m， I3=2 kg·m2。

本体的初始位姿为:(2 m，0 m，0 rad)。

关节角初始值:θ1=π/6，θ2=π/3，θ3=π/2。

末端的初始位姿为:(2 m，2 m，0 rad)。末端期望轨迹为一个圆:

选取1 000对不确定性非线性项的输入、输出数据，作为SVM的训练样本和测试样本集，其中700对数据用于训练，300对数据用于测试。选择ε-SVR类型的SVM，核函数类型为RBF函数，惩罚因子为2.2，核参数为0.1，松弛变量因子为0.01。选取Λ=3E3，p=5，q=3，Kv=5。其中E3为单位矩阵。仿真时间为5 s。仿真实验结果如图3～图7所示。

图3 系统不确定非线性项及其SVM估计Fig.3 Uncertain nonlinear term of the system and its SVM estimation

图4 未进行不确定非线性补偿的轨迹跟踪误差Fig.4 Trajectory tracking error without uncertainty nonlinear compensat

图5 进行SVM不确定非线性补偿的轨迹跟踪误差Fig.5 Trajectory tracking error with uncertainty nonlinear compensation

图6 未进行不确定性补偿的末端位置跟踪Fig.6 Position tracking of the end without uncertainty nonlinear compensation

图7 进行SVM不确定性补偿的末端位置跟踪Fig.7 Position tracking of the end with uncertainty nonlinear compensation

图3中逼近误差Δ f非常小，表明经样本训练的SVM可以很好地逼近实际模型，且满足Kv≥F的要求。图4、图5为末端轨迹跟踪误差曲线，其跟踪目标轨迹所需的时间分别为0.2 s和1 s，可见，采用SVM不确定非线性补偿方法提高了系统的动态性能，节省了末端跟踪目标轨迹的调节时间。比较图6和图7可看出，经SVM补偿系统较未补偿的系统的动态性能得到了提高。仿真结果表明，笔者设计的基于SVM不确定非线性补偿的滑模控制律是有效的，也说明了SVM具有很快的学习速度和很好的模型复现能力。

5 结 语

笔者针对自由漂浮空间机器人模型的不确定非线性特性，提出了一种基于SVM不确定非线性补偿的滑模控制方法。结合3关节空间机械臂系统建立了仿真模型，并基于Lyapunov理论证明了闭环系统的稳定性。仿真结果证实了SVM的非线性函数快速逼近能力，表明了此控制器避免了对空间机器人动力学模型的参数线性化要求以及设计控制器的繁多计算。仿真结果还表明，空间机械臂的轨迹跟踪动力学性能得到了提高，从而证明了控制方法的可行性和有效性。

［1］YOSHIDA K，HASHIZURME K，ABIKO S.Zero Reaction Maneuver Flight Validation with ETS-VII Space Robot and Extension to Kinemat-Iccally Redundant Arm［C］//Proceedings of the IEEE International Conference on Robotics and Automation.Piscataway，USA:［s.n.］，2011:441-446.

［2］洪昭斌，陈力.基于神经网络的漂浮基空间机械臂的自学习模糊控制［J］.机械科学与技术，2009，28(7):976-980.HONG Zhaobin，CHEN Li.Self-Learning Fuzzy Control of A Free-Floating Space Manipulator Based on Neural Network［J］.Mechanical Science and Technology for Aerospace Engineering，2009，28(7):976-980.

［3］KONSTANTIN V，ZMEU ELIYAA SHIPITKO，REY S PEREVOZCHIKOV.Linear Neural Model-Based Predictive Controller Design for Flexible Link Robot［C］//Proceedings of the 2004 IEEE International Symposium of Intelligent Control.Taipei，Taiwan:［s.n.］，2004:293-298.

［4］NGUYEN V B，MORRIS A S.Using a Genetic Algorithm to Fully Optimize a Fuzzy Logic Controller for a Two Link Flexible Robot Arm［J］.Robotic，2009，27(5):677-687.

［5］谢箭，刘国良，颜世佐，等.基于神经网络的不确定性空间机器人自适应控制方法研究［J］.宇航学报，2010，31(1):123-129.XIE Jian，LIU Guoliang，YAN Shizuo，et al.Study on Neural Network Adaptive Control Method for Uncertain Space Manipulator［J］.Journal of Astronautics，2010，31(1):123-129.

［6］高宏宇，邵克勇，李艳辉.不确定系统的上界自适应动态神经滑模控制［J］.吉林大学学报:信息科学版，2010，28(3):292-297.GAO Hongyu，SHAO Keyong，LI Yanhui.Upper Bound Adaptive Dynamic Neural Sliding Mode Control of Uncertain Systems［J］.Journal of Jilin University:Information Science Edition，2010，28(3):292-297.

［7］张文辉，高九州，马静，等.漂浮基空间机器人的径向基神经网络鲁棒自适应控制［J］.智能系统学报，2011，6(2):114-118.ZHANG Wenhui，GAO Jiuzhou，MA Jing，et al.The RBF Neural Network Robust Adaptive Control of a Free-Floating Space Robot［J］.CAAI Transactions on Intelligent Systems，2011，6(2):114-118.

［8］吴玉香，王聪.不确定机器人的自适应神经网络控制与学习［J］.控制理论与应用，2013，30(8):990-997.WU Yuxiang，WANG Cong.Adaptive Neural Network Control and Learning for Uncertain Robot［J］.Control Theory ＆Applications，2013，30(8):990-997.

［9］MANOJ MITTAL，CHUANG C H，JUANG JER-NAN.Nonlinear Control of Space Manipulators with Model Uncertainty［C］//The American Institute of Aeronautics and Astronautics.Langley Research Center，Hampton，VA:［s.n.］，1994:1009-1019.

［10］YOJI UMETANI，KAZUYA YOSHIDA.Resolved Motion Rate Control of Space Manipulators with Generalized Jacobian Matrix［J］.IEEE Transactions on Robotics and Automation，1989，5(3):303-314.

［11］JONGHO SHIN，H JIN KIM，YOUDAN KIM.Adaptive Support Vector Regression for UAV Flight Control［J］.Neural Networks，2011，24(1):109-120.

(责任编辑:何桂华)

Research on SVM Nonlinear Estimation Sliding Mode Control of Space Robot

DENG Yulong，WANG Congqing
(School of Automation，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China)

A method of sliding mode control based on SVM(Support Vector Machine)nonlinear estimation of the robotic dynamics has been proposed to acquire faster trajectory tracking rate of the space manipulator end.SVM regression is used to estimate the parameter uncertainty of the nonlinear term and to compensate dynamic model of space robot.This SVM nonlinearity compensated sliding mode controller designed on the stability of the closedloop system，avoiding computing precise model，has improved the dynamics performance of the system，achieving faster target trajectory tracking rate and reducing the tracking error.The simulation results show that the presented method is effective and feasible.

space robot;support vector machine(SVM);nonlinear estimation;sliding mode control

TP242

A

1671-5896(2014)02-0166-06

2013-12-02

西安交通大学机械制造工程国家重点实验室基金资助项目(201002)

邓玉龙(1988— )，男，湖南永州人，南京航空航天大学硕士研究生，主要从事空间机器人控制研究，(Tel)86-15195765149(E-mail)dengyu_long@126.com;王从庆(1960— )，男，南京人，南京航空航天大学教授，硕士生导师，主要从事智能控制及应用研究，(Tel)86-13151426390(E-mail)wangcq@nuaa.edu.cn。