主成分分析与聚类分析在青岛夏季气温变化研究中的应用
2014-09-09屈家安曹杰
屈家安,曹杰
(南京信息工程大学,江苏 南京 210044)
主成分分析与聚类分析在青岛夏季气温变化研究中的应用
屈家安,曹杰
(南京信息工程大学,江苏 南京 210044)
选用青岛站1951—2010年每年 6—8月各月平均气温资料,通过SAS软件进行了主成分分析和聚类分析,分析了近60 a夏季气温的年际气候变化。主成分分析的结果表明,第一主成分反映青岛夏季气温距平,其正(负)方向反映夏季气温的正(负)距平,其强度反映气温偏高(低)的程度;第二主成分则反映同一年内夏季各月间气温的差异,其绝对值越大,表示各月气温差异越大。聚类分析的结果表明,青岛站夏季月平均气温的变化可以分为3类:1)6月、7月气温较低,在8月升温;2)7月平均气温最高,6月、8月相对较低;3)6月气温低,7、8两月气温较高。其中1993、2003年为第一类,2005年为第二类,其余为第三类。
主成分分析;聚类分析;SAS软件;气象应用
0 引言
多元统计分析在我国气象业务预报和科研工作中起着重要的作用,特别是在数值预报产品的统计使用及中长期预报业务中,统计方法更是扮演着一个重要的角色,多元统计分析中的主成分分析和聚类分析等也是气象预报和分析不可缺少的工具(谢炯光等,2003)。主成分分析方法是在一组变量中找出其方差和协方差矩阵的特征量,把多个变量通过降维的方法转化为少数几个综合变量的统计分析方法(Moshonas and Shaw,1997;Korre,1999;高吉喜等,2006),可以找出几个综合因子来代表原来众多的气象要素,避免了各个气象因子间存在交叉重叠信息,从而达到简化的目的(尹云鹤等,2009;李宗省等,2010;王少鹏等,2010)。聚类分析方法是指将物理或抽象对象的集合分组成为由类似对象组成的多个类的方法,在气象数据获取、处理和应用流程中运用聚类分析方法,可发现其中具有内在联系的规则或模式,为科学决策提供更好的服务(Bock,1985)。
近年来,计算机技术的发展促进了社会的信息化进程,也促进了多元统计方法的软件化进程,各种统计分析软件的出现使气象科研和预报人员处理大量数据变得得心应手,极大地提高了工作效率。SAS(statistical analysis system)软件系统是大型集成应用系统,功能齐全而且强大,具有完备的数据访问、数据管理、数据分析、报告编制和数据呈现功能,不仅在统计分析、时间序列分析、运筹决策上功能强大,并可将各种数据以灵活多样的各种报表、图形和三维透视的形式直观地表现出来,而且在数据的处理上也显示了比较强的优势(李够霞,2002)。本文使用SAS软件对青岛地区近60 a气温进行主成分分析和聚类分析。
气候变暖是当前国内外科学研究及全球媒体关注的热点问题(易湘生等,2011)。但众多研究表明,全球气温变化在不同区域存在着明显的区域差异(理查德和迪安,2001;于秀林和任雪松,2003;张尧庭和方开泰,2003;陈效逑等,2009)。青岛是中国最早开展气象观测的站点之一,气温序列是连续的。青岛的气温数据能够真实地反映青岛地区的升温情况,对山东乃至华东和华北地区都有很好的借鉴意义。另外,青岛是中国经济发达城市,在东部沿海具有代表性,其气候变迁和气温变化对其旅游经济具有一定的影响,因此,研究青岛气温的变化有着较高的现实意义(庞华基等,2007)。
1 资料与方法
选用青岛站1951—2010年共60 a 6—8月各月平均气温资料。资料来自国家气候中心气候系统诊断预测室提供的全国160站月气温和降水资料。
1.1 主成分分析
主成分分析是通过构造原变量的线性组合,产生一系列互不相关的新变量,从中选出少数几个新变量使他们含有尽可能多的原变量信息,从而以较少新变量代替原来较多变量,消除信息冗余,实现模型的简化(曹彦龙等,2007;张旋等,2010)。主成分分析也可以实现计算原变量的重要性系数进行排序,达到筛选变量降低模型维数的目的(张建伟等,2011)。主成分分析的数学模型(吴诚鸥和秦伟良,2007)是:对于随机向量X,选一些常数向量ci,用ci′X尽可能多反映随机向量X的主要信息,也即D(ci′X)尽量大。但是ci的模可以无限增大,从而使D(ci′X)无限变大,这是不利的,于是限定ci模的大小,而改变ci各分量的比例,使D(ci′X)最大;通常取ci的模为1最方便。
当随机向量方差已知时,主成分的计算公式为:设随机向量X=(X1,…Xp)′方差存在为Σ。Σ特征值从大到小为λ1≥λ2≥…≥λp,λj对应的彼此正交单位特征向量为cj。则X的第j个主成分Yj为cj与X的内积,即Yj=cj′X,且Yj的随机变量方差为λi。
1.2 聚类方法
聚类方法根据观测对象之间的彼此相似程度达到“物以类聚”的目的(António,2002),其原则是根据事物本身的特征研究个体分类的方法(Glenn,1981;Forner-Cordero et al.,2005)。聚类分析运用数学方法对不同的样本进行数字分类,定量的确定样本间的亲属关系,并按照他们之间的相似程度,归组并类(胡娅敏等,2010)。本文使用的聚类分析方法为类平均法(average linkage method)(吴诚鸥和秦伟良,2007):d(x,y)=‖x-y‖2为观测样本的欧氏距离。类平均法有两种定义:一种定义方法是把类与类之间的距离定义为所有样品对之间的平均距离,即定义Gk和Gl之间的距离为
其中nk和nl分别为类Gk和Gl的样品个数。
当某类Gk和Gl合并成一个新类Gm,计算Gm与任一类Gj的距离,其递推公式为

另一种定义方法是定义类与类之间的平方距离为样品对之间平方距离的平均值,即
在上面的递推公式中,Dkj没有被反映出来,为此可将该公式进一步推广为
其中β<1,称这种系统聚类法为可变类平均法。
2 结果分析
2.1 主成分分析结果
使用SAS软件。因为所有变量单位相同,可用协方差阵求主成分。以变量T6、T7、T8分别表示6、7、8月的平均气温(程序略)。
表1为所得的基本统计量。由表1可见,7月气温的标准差最大,说明数据的离散度最大,亦即7月气温的波动范围较其他两个月大,气温不稳定。
表1基本统计量
Table 1 Simple statistics ℃

月份气温平均值标准差620.586666670.78361757724.413333331.04888426825.298333330.83208777
所得样本协方差矩阵为

表2为样本协方差矩阵的特征值,前两个特征值累计方差贡献率达到84.76%,因此取前两个主成分。
表2样本协方差矩阵的特征值表
Table 2 Eigenvalues of the covariance matrix

主成分特征值方差贡献率/%累计方差贡献率/%11.5789686865.6165.6120.4608297519.1584.7630.3667863215.24100.00
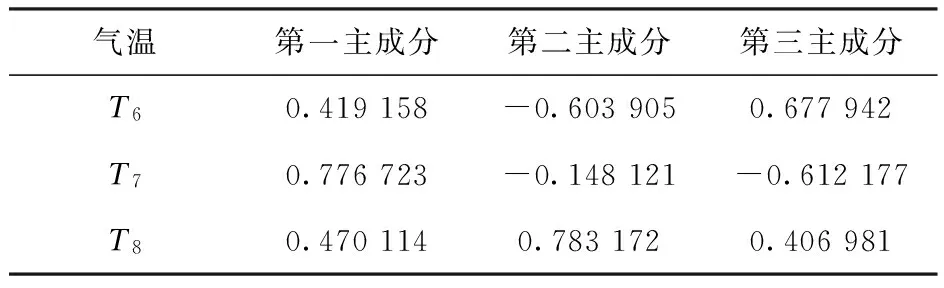
表3给出了样本协方差矩阵的特征向量。
表3样本协方差矩阵的特征向量
Table 3 Eigenvectors of the covariance matrix
气温第一主成分第二主成分第三主成分T60.419158-0.6039050.677942T70.776723-0.148121-0.612177T80.4701140.7831720.406981
根据特征向量构建主成分与气温之间的线性关系:
y1=0.419 158T6+0.776 723T7+0.470 114T8,
y2=-0.603 905T6-0.148 121T7+0.783 172T8,
y3=0.677 942T6-0.612 177T7+0.406 981T8。
由线性关系可见,第一主成分中系数均为正,且T6、T8系数较小,T7系数较大,说明相较于6、8月,7月气温的影响更大。第一主成分反映了青岛夏季气温距平,其正(负)方向反映夏季气温的正(负)距平,其强度反映气温偏高(低)的程度。因此,当第一主成分值较大时,说明夏季气温偏高程度较高。
第二主成分T6系数与T8系数符号相反且绝对值均比较大,说明第二主成分主要表示6月与8月温度距平的差异,即6月温度距平与8月温度距平的差值。因此,第二主成分反映了同一年内夏季各月间气温的差异,其绝对值越大,表示各月气温差异越大。
由主成分得分表(表略)可见:1994年第1主成分最强(夏季气温偏高),1976年第1主成分负方向最强(夏季气温偏低),1952年第1主成分绝对值最小(夏季气温最接近常年);1951年第2主成分最强(8月比6月气温高得多),2005年第2主成分负方向最强(8月气温与6月气温差值较小),2000年第2主成分绝对值最小(8月气温与6月气温差接近历年平均值)。
2.2 聚类分析结果
使用类平均法对6、7、8三个月的平均气温进行聚类分析,以年区分聚类的观测。图1为聚类树形图,可见,可将青岛1951—2010年共60 a夏季月平均气温的变化分成三类:1993、2003年为第一类,2005年为第二类,其余年份为第三类。
第一类为6、7月温度较低,8月气温较高;第二类是2005年,7月平均气温高而6、8月相对较低;其余年份归为第三类,即6月气温低,7、8两月气温较高。

图1 聚类树形图Fig.1 The cluster tree diagram
3 结论
青岛的气温数据对山东乃至华东和华北地区都有很好的借鉴意义,在东部沿海具有代表性,青岛地区的气候变迁和气温变化对其旅游经济具有一定的影响。本文选用了青岛站1951—2010年共60 a每年6—8月的各月平均气温资料进行主成分分析和聚类分析,结果表明:
1)第一主成分反映青岛夏季气温距平,其正(负)方向反映夏季气温的正(负)距平,其强度反映气温偏高(低)的程度;第二主成分则反映同一年内夏季各月间气温的差异,其绝对值越大,表示各月气温差异越大。
2)聚类分析表明,青岛站夏季月平均气温的变化可以分为三类:第一类在6、7月气温较低,8月升温;第二类为7月平均气温最高而6、8月相对较低;第三类为6月气温相对较低,7、8两月气温较高。其中1993、2003年为第一类,2005年为第二类,其余为第三类。
主成分分析和聚类分析等多元统计分析方法在气象预报和研究中发挥着重要作用,采用SAS软件系统进行气象资料的主成分分析和聚类分析,对研究气温的年际气候变化有一定的帮助,利用SAS软件得出的统计分析结果具有实际意义,可极大地提高气象资料分析的效率。
曹彦龙,李崇明,阚平.2007.重庆三峡库区面源污染源评价与聚类分析[J].农业环境科学学报,26(3):857-862.
陈效逑,彭嘉栋,李慧敏.2009.内蒙古地区气温变化的季节和区域差异[J].地理研究,28(1):27-35.
高吉喜,段飞舟,香宝,等.2006.主成分分析在农田土壤环境评价中的应用[J].地理研究,25(5):836-842.
胡娅敏,丁一汇,廖菲.2010.近52年江淮梅雨的江水分型[J].气象学报,68(2):235-247.
理查德,迪安.2001.实用多元统计分析[M].4版.北京:清华大学出版社.
李够霞.2002.SAS软件在气象数据处理中的应用[J].计算机与农业,17(6):33-35.
李宗省,何元庆,辛惠娟,等.2010.我国横断山区1960—2008年气温和降水时空变化特征[J].地理学报,65(5):563-579.
庞华基,高靖,李春,等.2007.青岛百年气温变化及其影响因素分析[J].南京气象学院学报,30(4):524-529.
王少鹏,王志恒,朴世龙,等.2010.我国 40年来增温时间存在显著的区域差异[J].科学通报,55(16):1538-1543.
吴诚鸥,秦伟良.2007.近代实用多元统计分析[M].北京:气象出版社.
谢炯光,曾琼,纪忠萍.2003.中国近30年来气象统计预报进展[J].气象科技,31(2):67-83.
易湘生,尹衍雨,李国胜,等.2011.青海三江源地区近50年来的气温变化[J].地理学报,66(11):1451-1465.
尹云鹤,吴绍洪,陈刚.2009.1961—2006年我国气候变化趋势与突变的区域差异[J].自然资源学报,24(12):2147-2157.
于秀林,任雪松.2003.多元统计分析[M].北京:中国统计出版社.
张建伟,王根,张华,等.2011.基于主成分累计影响系数法的高光谱大气红外探测器的通道选择试验[J].大气科学学报,34(1):36-42.
张旋,王启山,于淼,等.2010.基于聚类分析和水质标识指数的水质评价方法[J].环境科学学报,4(2):476-480.
张尧庭,方开泰.2003.多元统计分析引论[M].北京:科学出版社.
António P D S.2002.Discarding variables in a principal component analysis:Algorithms for all-subsets comparisons[J].Computational Statistics,17(2):251-271.
Bock H H.1985.On some significance tests in cluster analysis[J].Journal of Classification,2(1):77-108.
Forner-Cordero A,Levin O,Li Y,et al.2005.Principal component analysis of complex multijoint coordinative movements[J].Biological Cybernetics,93(4):63-78.
Glenn W M.1981.A monte carlo study of thirty internal criterion measures for cluster analysis[J].Psychometrika,46(2):187-199.
Korre A.1999.Statistical and spatial assessment of soil heavy metal contamination in areas of poorly recorded,complex sources of pollution,Part 1:Factor analysis for contamination assessment[J].Stochastic Environmental Research and Risk Assessment,13:260-287.
Moshonas M G,Shaw P E.1997.Dynamic headspace gas chromatography combined with multivariate analysis to classify fresh and processed orange juices[J].Journal of Essential Oil Research,9(2):133-139.
(责任编辑:张福颖)
ApplicationofprincipalcomponentanalysisandclusteranalysisinastudyonthechangeofsummertemperatureinQingdao
QÜ Jia-an,CAO Jie
(Nanjing University of Information Science & Technology,Nanjing 210044,China)
Interannual change of summer temperature in Qingdao was analyzed based on the monthly average temperature data during June and August in 1951—2010 by using the method of principal component analysis and cluster analysis through SAS software.According to principal component analysis,the first principal component was the summary of summer temperature departure in Qingdao.The positive(negative) direction reflected the positive(negative) anomaly of temperature and the strength reflected its degree.The second principal component reflected the temperature difference among each month of the same year.The larger the absolute value of the second principal component was,the greater the temperature difference among each month was.Cluster analysis showed that the change of average monthly temperature in summer in Qingdao could be divided into three categories.The first type was that the temperature was low in June and July and warmed up in August.The second type was that the average temperature in July was the highest while in June and August it was relatively low.The third category was that the temperature in June was low and it got high in both July and August.The year of 1993 and 2003 were of the first type,2005 of the second type and the other years of the third type.
principal component analysis;cluster analysis;SAS software;applications in meteorology
2013-05-15;改回日期2013-10-07
国家自然科学基金资助项目(71101073)
屈家安,博士生,副研究员,研究方向为气象灾害应急决策,qujiaan@nuist.edu.cn.
10.13878/j.cnki.dqkxxb.20130515005.
1674-7097(2014)04-0517-04
P468
A
10.13878/j.cnki.dqkxxb.20130515005
屈家安,曹杰.2014.主成分分析与聚类分析在青岛夏季气温变化研究中的应用[J].大气科学学报,37(4):517-520.
Qü Jia-an,Cao Jie.2014.Application of principal component analysis and cluster analysis in a study on the change of summer temperature in Qingdao[J].Trans Atmos Sci,37(4):517-520.(in Chinese)
