基础刚度对天线结构系统固有频率的影响

陈庚超，徐曙斌

(中国电子科技集团公司第三十九研究所， 陕西 西安 710065)

基础刚度对天线结构系统固有频率的影响

陈庚超，徐曙斌

(中国电子科技集团公司第三十九研究所， 陕西 西安 710065)

在天线结构系统设计中，为了提高结构系统的固有频率，往往对基础的固有频率提出明确的指标要求，却未对基础的刚度提出明确要求。文中从两自由度串联弹簧质量系统固有频率的计算公式出发，推导了基础刚度与天线结构系统固有频率之间的关系式，证明了提高基础刚度比提高基础固有频率更能有效地提高天线结构系统的固有频率。文中还给出了根据天线结构自身固有频率和天线结构系统固有频率确定基础刚度指标的方法并对该方法的有效性进行了论述。

天线；固有频率；基础刚度

引 言

自动控制理论揭示了天线结构系统固有频率与伺服带宽的关系[1]，要提高天线伺服系统的精度，就必须提高伺服系统的带宽。然而随着测控和通讯技术的发展，天线的口径越来越大，使天线结构的固有频率下降，逐步靠近甚至落入伺服带宽之内。在这种情况下，各种伺服噪声就会激发系统发生谐振，而反馈又会使谐振持续下去，造成伺服系统不稳定，无法工作，甚至损坏结构。为了保证天线伺服系统的稳定性，通常要求天线结构系统的固有频率高于伺服带宽3～5倍[2]。因此，在进行天线结构系统设计时，必须满足对天线结构系统固有频率的指标要求，提高天线结构系统的固有频率是天线结构设计所追求的目标之一。

要提高天线结构系统的固有频率，首先就需要明确天线结构系统的固有频率与哪些因素有关。前人的研究成果和文献[3]从不同角度给出了一些结论，揭示了天线结构系统固有频率与天线结构自身固有频率和基础固有频率之间的关系。从这些文献可知，以前主要通过提高天线结构刚度，减小惯量来提高天线结构自身的固有频率，另外就是通过提高基础的固有频率来提高天线结构系统的固有频率，不因基础的固有频率偏低而使整个天线结构系统的固有频率明显下降，以保证天线结构系统的固有频率满足设计要求。

这些研究的不足之处在于没有全面揭示天线结构系统的固有频率与基础各要素之间的关系。天线结构系统的固有频率不仅与基础的谐振频率有关，还与基础的刚度有关，即使天线结构本身和基础的固有频率较高，如果基础的刚度较低，也会使包含基础的天线结构系统的固有频率显著下降，甚至不能满足要求。为了防止天线结构系统固有频率因基础刚度不足而显著下降，需要对基础刚度提出明确的指标要求。本文进一步从理论上揭示了天线结构系统的固有频率与基础刚度之间的关系，并给出了反映它们之间数值关系的对照表，以方便天线结构设计人员参考。

1 基础刚度与天线结构系统固有频率的关系

本文从两自由度串联弹簧质量系统的固有频率计算公式出发，推导出了包含基础的天线结构系统的固有频率与基础刚度之间的关系式。如图1所示,单自由度弹簧质量系统的扭转刚度为K，转动惯量为J，其扭转固有频率的关系式[2]为

ω2=K/J

(1)

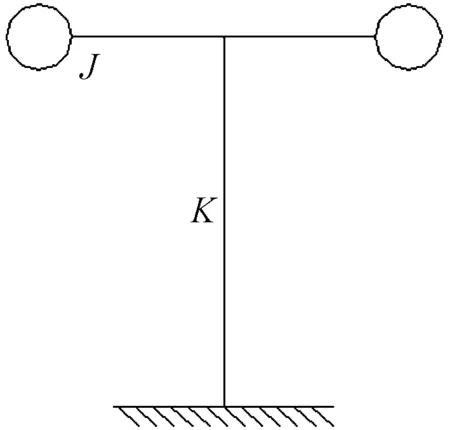
图1 单自由度弹簧质量系统示意图

设天线结构的扭转刚度为K1，转动惯量为J1，则其扭转固有频率为

(2)

设基础的扭转刚度为K2，转动惯量为J2，则其扭转固有频率为

(3)

将天线安装在基础上的情形看作是天线和基础串联形成的两自由度弹簧质量系统，如图2所示，其1阶扭转固有频率[2]为

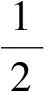
(4)

图2 两自由度弹簧质量系统示意图

将式(2)和式(3)代入式(4)，可得：

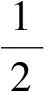
(5)

令基础固有频率与天线固有频率之比ω2/ω1=P，即

ω2=Pω1

(6)

将式(6)代入式(5)可得：

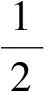
(7)

令基础刚度与天线刚度之比K2/K1=R，即

K1=K2/R

(8)

将式(8)代入式(7)可得：

(9)

由式(9)可得到包含基础的天线结构系统的固有频率与天线结构自身固有频率的比值：

该式揭示了天线结构系统的固有频率和基础刚度之间的关系。

式(10)对R求导数可得：

ω/ω1的值与天线基础和天线结构自身固有频率的比值P及天线基础和天线结构自身刚度的比值R有关。式(11)的值大于0，所以ω/ω1的值相对于R为单调递增函数。也就是说，在天线结构自身的刚度和固有频率以及基础固有频率不变的情况下，随着基础刚度的提高，包含基础的天线结构系统的固有频率也会提高。

从理论上讲，串联形式的两自由度弹簧质量系统的固有频率低于构成它的任一单自由度弹簧质量系统的固有频率。因此，随着基础刚度的相对提高，包含基础的天线结构系统的固有频率相对于天线结构自身的固有频率下降的百分比减小。所以为了防止天线结构系统固有频率因基础刚度不足而显著下降，需要对基础刚度提出明确的指标要求，即基础刚度必须大于某一规定的数值。

2 基础刚度指标的确定

在实际工程应用中，天线结构设计单位应向基础设计建设单位提出天线基础固有频率和刚强度指标要求。为了方便工程应用，本文根据式(10)，以表格的形式给出了在不同P值(天线基础和天线结构自身固有频率的比值)和R值(天线基础和天线结构自身刚度的比值)条件下，包含基础的天线结构系统的固有频率与天线结构自身固有频率的比值ω/ω1，见表1。

表1 不同P值和R值下天线结构系统与天线结构自身固有频率的比值(ω/ω1)

R值P=1P=2P=3P=4P=5 R=10．61803040．68474160．69722440．70156210．7035627 R=20．70710680．79228700．80610830．81072850．8128275 R=30．75215790．84351250．85657380．86081580．8627226 R=40．78077640．87403200．88600090．88980680．8915047 R=50．80108830．89442720．90534290．90875870．9102743 R=60．81649660．90906600．91904610．92213050．9234933 R=70．82871830．92010310．92927050．93207560．9333109 R=80．83872810．92873110．93719500．93976380．9408920 R=90．84712710．93566550．94351880．94588610．9469236 R=100．85430900．94136300．94868330．95087730．9518371

从表1可以看出：天线结构系统的固有频率与天线结构自身固有频率的比值ω/ω1随着P值和R值的增大而增大，即提高基础的固有频率和基础的刚度都可以使天线结构系统的固有频率得到提高。但是从表中的数据可以看出：提高基础的刚度对提高天线结构系统的固有频率比提高基础的谐振频率更有效。当天线自身的刚度和基础的刚度相同时，基础固有频率提高到原来的5倍，天线结构系统的固有频率降低到天线自身固有频率的70.4%；而当天线自身的固有频率和基础的固有频率相同时，基础刚度提高到原来的5倍，天线结构系统的固有频率只降低到天线自身固有频率的80.1%。

结构形式是对结构固有频率影响最大的因素。在结构形式确定的情况下，提高天线结构自身的固有频率或者基础的固有频率是比较困难的，需要付出很大的代价。相对来说，提高基础的刚度要容易得多。假设某一天线基础的结构形式确定为空心圆台结构，如果将其壁厚增加1倍，其固有频率变化不大，但其刚度会提高约1倍。基础一般为钢筋混凝土结构，提高其刚度付出的代价相对较小，也相对容易操作。

根据表1可以方便地确定天线基础的刚度指标。通常对基础设计建设单位提出的基础固有频率指标为不低于天线结构自身固有频率的2～3倍。假设要求基础的固有频率是天线结构固有频率的3倍，天线安装到基础上后，要求天线结构系统的固有频率最多下降到天线结构原固有频率的90%，则从表1可知，基础刚度必须达到天线结构刚度的5倍才能满足要求；假设天线结构固有频率的富余量较大，允许天线安装到基础上后天线结构系统固有频率下降到天线结构原固有频率的85%，则从表1可知，基础刚度必须达到天线结构刚度的3倍才能满足要求。

从经济性角度来说，对基础的固有频率和刚度指标的要求不能过高，指标高必然会增加天线基础的建造难度和成本。因此应予以综合考虑，所定指标满足设计要求并有适当裕度即可。

3 基础刚度与天线结构系统固有频率测试

在当前的实际工程应用中，天线结构设计单位通常会向基础设计建设单位提出天线基础固有频率和强度指标要求，但并不明确提出刚度指标要求。原因是基础要满足天线结构在重力、风载等或组合工况下对它的强度指标要求，就必须“身强力壮”，这就同时满足了对基础刚度的要求。但这不是绝对的，如果某种情况对基础的强度要求较低，就可能导致基础满足固有频率和强度指标要求，但刚度却较低，最后使包含基础的天线结构系统的固有频率下降太多，不满足指标要求。为了防止这种情况的发生，最好还是对基础的刚度也提出明确的要求。

对基础、天线结构自身或两者组合在一起的结构进行刚度测试，是一个非常困难的工作。目前工程上的处理方法是对结构进行简化等效处理，然后用结构力学的相关公式进行校核，或者用有限元软件进行仿真计算。对基础或基础与天线组合结构可进行固有频率测试，但却无法对天线结构自身单独进行固有频率测试，因为无法找到一个刚度足够且接口关系符合要求的天线安装平台。目前，对天线结构系统整体或部分进行的力学性能测试的数据还很少，找到的数据也仅限于基础固有频率和基础与天线组合在一起时的系统固有频率。

某研究单位用脉动法对基础固有频率和基础与天线组合在一起时的系统固有频率进行了测试。脉动法是利用高灵敏度的传感器、放大器及记录设备，通过联测由环境随机激振引起的结构物响应，借助随机信号数据处理技术，分析确定结构物的动态力学特性的方法。某12m口径抛物面天线的基础固有频率测试值为12.40 Hz，天线结构自身的固有频率计算值为12.8 Hz，两者的比值P接近1，基础与天线组合在一起时的系统固有频率测试值为10.06 Hz，与天线结构自身的固有频率的比值R约为0.80。对照表1可知，若基础刚度与天线结构刚度之比大约为5，则各测试或计算数据会与本文论述的各数据之间的关系相吻合。某26 m口径抛物面天线的基础固有频率测试值为20.94 Hz(仿真计算值为19.97 Hz)，天线结构自身的固有频率计算值为13.54 Hz，两者的比值P约为1.55，基础与天线组合在一起时的系统固有频率测试值为12.0 Hz，与天线结构自身的固有频率的比值R约为0.89。用式(10)进行计算，若基础刚度与天线结构刚度之比大约为5.7，则各测试或计算数据会与本文论述的各数据之间的关系相吻合。分析认为，通常情况下基础刚度会远高于天线结构自身的刚度，达到其五六倍的水平应是合理的。这从一定程度上佐证了本文所论述的基础刚度与天线结构系统固有频率之间关系的正确性。

由于无法得到基础结构设计的相关数据及相关测试数据不足，现阶段尚不能对本文所述内容进行充分验证。即便如此，把包含基础的天线结构系统简化为两自由度串联弹簧质量系统，并由此推出基础刚度与天线结构系统固有频率之间的关系表达式无疑是合理的，只是其精确性有待进一步分析论证，因为包含基础的天线结构系统显然是无限自由度的连续质量系统，将其简化为两自由度串联弹簧质量系统，肯定会带来一定的误差。

4 结束语

本文从两自由度串联弹簧质量系统固有频率的计算公式出发，论述了基础刚度对天线结构系统固有频率的影响，给出了根据天线结构自身固有频率和天线结构系统固有频率确定基础刚度指标的方法。该方法及总结的表格可以为天线设计工作带来方便，对解决工程实际问题具有一定的参考价值。所述的两自由度串联系统，既可看成是扭转刚度(对应转动惯量)的串联，也可看成是弯曲刚度(对应质量)的串联，所以其方法和结论对确定基础的扭转刚度和弯曲刚度均适用。

[1] 周立峰，巢来春. 伺服系统基本原理[M]. 北京：国防工业出版社，1980.

[2] 吴凤高. 天线座结构设计[M]. 北京： 国防工业出版社，1980.

[3] 中国电子科技集团公司第39研究所. 大型测控天线塔基与天线性能互作用分析技术报告[R]. 西安：中国电子科技集团公司第39研究所，2013.

陈庚超(1971-)，男，高级工程师，主要从事天线结构的设计和力学分析工作。

Influence of Foundation Stiffness on Inherent Frequency of Antenna Structure System

CHEN Geng-chao，XU Shu-bin

(The39thResearchInstituteofCETC,Xi′an710065,China)

In the antenna structure system design, in order to improve the inherent frequency of the system, clear requirement for the inherent frequency of the foundation is often put forward, but not for the stiffness of the foundation. From the formula to calculate the inherent frequency of the two degree of freedom spring mass series system, the relationship between the foundation stiffness and the inherent frequency of the antenna structure system is obtained. It is proved that increasing the foundation stiffness can improve the inherent frequency of the antenna structure system more effectively than increasing the inherent frequency of the foundation. The method to determine the index of the foundation stiffness is presented according to the inherent frequency of the antenna structure itself and the antenna structure system. And the effectiveness of the method is also discussed in this paper.

antenna; inherent frequency; foundation stiffness

2014-03-31

TN82

A

1008-5300(2014)04-0030-04