一种脉组间步进频雷达速度估计误差的改进方法

尹华桥，王顺喜

(1．中国电子科技集团公司第三十八研究所，合肥 230088；2. 61195部队，南京 210008)

一种脉组间步进频雷达速度估计误差的改进方法

尹华桥1，王顺喜2

(1．中国电子科技集团公司第三十八研究所，合肥 230088；2. 61195部队，南京 210008)

在脉组间步进频信号的脉组内利用傅里叶变换测速时，针对测速误差对合成距离像的影响，提出了二分迭代法。该方法通过log2N次迭代操作便可使测速精度提高N倍 (N为脉组个数)，通过相关补偿后的合成距离像的走动不超过半个距离分辨单元。此外，由于测速精度提高速率是以2为底的指数增长，且每次迭代为脉组内FFT操作，因此该方法具有较少的运算量。仿真实验验证了该方法的有效性。

步进频；速度误差；合成距离像；快速傅里叶变换

0 引 言

相比具有瞬时超宽带信号雷达，步进频信号在不需增加雷达硬件成本的情况下，通过慢时间维的快速傅里叶变换(Fast Fourier Transform, FFT)可获得合成的一维距离像[1-3]，达到增加信号带宽、提高目标距离分辨力的效果。因此，步进频信号在目标分类识别等方面具有良好的应用前景[4-5]。然而，该信号存在距离-多普勒耦合，使得存在相对径向运动的目标距离像沿距离维走动以及扩展[6]，而且该信号不能利用FFT直接测速。基于此，文献[6]研究了脉组间步进频信号，即与各脉组内发射与当前频率一致的脉冲串。该信号通过在脉组内的FFT处理及脉组间的逆傅里叶变换(Inverse Fast Fourier Transform, IFFT)的二维信号处理，可分别得到目标速度估计值和合成一维距离像。但是，脉组间频率的步进引入了多普勒色散(多普勒随不同脉组下的频率变化而发生变化)以及测速时的量化误差对距离像的影响。于是，文献[7]利用脉组间步进频信号分析了多普勒滤波器组输出的相位和幅度值对合成距离像的影响，但未考虑由距离-多普勒耦合导致的距离移动与能量在距离维上的扩展，以及径向速度的估计。然而，对目标速度的分析是设计脉组间步进频信号的初衷及重要研究内容。

为此，在文献[6]基础上，本文针对测速误差对距离像的影响，提出二分迭代法(Dimidiate Iterative Method, DIM)，以进一步提高测速精度，使得补偿距离-多普勒耦合后获得满足要求的合成高分辨距离像(距离走动在半个分辨单元内)。

1 回波信号模型

设脉组间步进频信号中第一个脉冲串的载频为f0、频率增长步长为△f、脉组个数为N、脉组内脉冲间隔PRI为Tp(即由c/(2v0f0)确定的恒定值)、脉冲宽度为τ以及脉冲个数为M，v0为第一个脉组对应的目标最大不模糊速度，则相干处理间隔(CPI)Ts为MTp。该信号示意图如图1所示。

由图1可得其复信号数学表达式

(1)

其中，A为发射信号幅度值，fn=f0+n△f，rect(·)为脉冲宽度为τ的矩形函数。

由文献[8]所述，采取脉组间参差PRI，以消除由脉组间频率变化引起的多普勒色散对合成距离像的走动以及形变的影响。脉组间参差PRI指各脉组内的PRI由当前频率确定，为了区别由c/(2v0f0)确定的非参差PRITp，现将第n个脉组对应的PRI表示为Tnp=c/(2v0fn)，则相应的CPITs变为Tns=MTnp。于是，经过脉组间参差PRI，并对回波进行抽样后的基频信号可表示为[7]

(2)

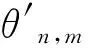
(3)

对式(3)中第n个脉组内进行FFT，可得

(4)

其中i=1,2, …,M。

从式(4)可知，通过脉组间参差PRI处理后，式(4)中第2个等号右边的第2项中不包含与脉组序号n相关的参量，即消除了多普勒色散对距离像的影响[7]。

2 速度估计误差对距离像影响分析

(5)

则利用式(5)补偿式(4)中对应的距离-多普勒耦合项，可得

(6)

对补偿后的式(6)进行脉组间的IFFT处理，得到补偿后的目标距离像。

其中k=1,2, …,N。

(8)

及

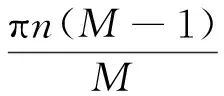
(9)

而当不采用脉组间参差PRI处理时，相应的补偿相位误差为

(10)

由式(10)中不等式右边的第2项(二次项)可得N需满足[6]

(11)

和式(10)相比，采用脉组间参差PRI获得的式(9)没有如式(10)中的二次项，即脉组个数N没有如式(11)所示的限制条件。于是，当△f一定时，可以改变N值，以获得需要的距离分辨率△R=c/2(N△f)。这是采用脉组间参差PRI的另一优点。

(12)

由式(12)可得测速的最大量化误差导致目标距离像移动的分辨单元个数l为

(13)

其中round(·)表示四舍五入。由式(13)可知，尽管利用FFT的速度估计值进行了相关补偿，但当该速度估计值存在最大测速误差时，仍会导致距离像沿距离维移动高达round(N/2)个距离分辨单元。因此，对于获得合成高分辨距离像而言，进一步研究如何提高测速精度以减小量化误差对距离像的不良影响是十分必要的。

3 基于二分迭代法的测速误差的改善

根据式(13)可知，由于通过脉组内FFT获得的速度存在量化误差，通过对距离-多普勒耦合进行相应补偿后的距离像仍有可能移动多个分辨单元。

为此，在FFT估计目标径向速度的基础上，提出二分迭代法DIM以提高测速精度。该方法的基本思路为：

(1) 根据式(4)获得的速度值确定目标速度所在的初始分辨单元，从而得到相应的初始速度范围；

(2) 对该速度范围平均一分为二处理，由此可知目标真实速度位于二分范围的左半区间或者右半区间；

(3) 在该速度(由式(4)获得)上附加当前速度范围的二分之一对应的值，在脉组内FFT处理后，通过观测和对比附加后及附加前的速度峰值位置变化，若该位置对应的分辨单元增加一个，则目标真实速度位于右半区间，否则位于左半区间，从而可使真实速度所处的范围缩小一半；

(4) 重复步骤(2)和(3)进行二分迭代运算，使得速度估计值逼近真实值，以最终获得所需的测速精度，即最大测速误差对应的距离移动不超过距离分辨单元的一半。之所以称该方法为“二分迭代”法，是基于步骤(2)的二分处理和步骤(4)的迭代操作。

(14)

(15)

对式(15)进行脉组间的IFFT处理，即

(16)

由式(16)可知，采取DIM后，若补偿距离-多普勒耦合后的距离像移动不超过半个距离单元，则需满足

(17)

其中N为脉组间步进频信号的脉组个数。由式(17)可看出，当利用DIM后测速精度提高倍数不低于N时，经距离-多普勒耦合补偿后，距离像移动不超过半距离单元，从而可终止迭代运算。DIM处理流程可归纳见图2。

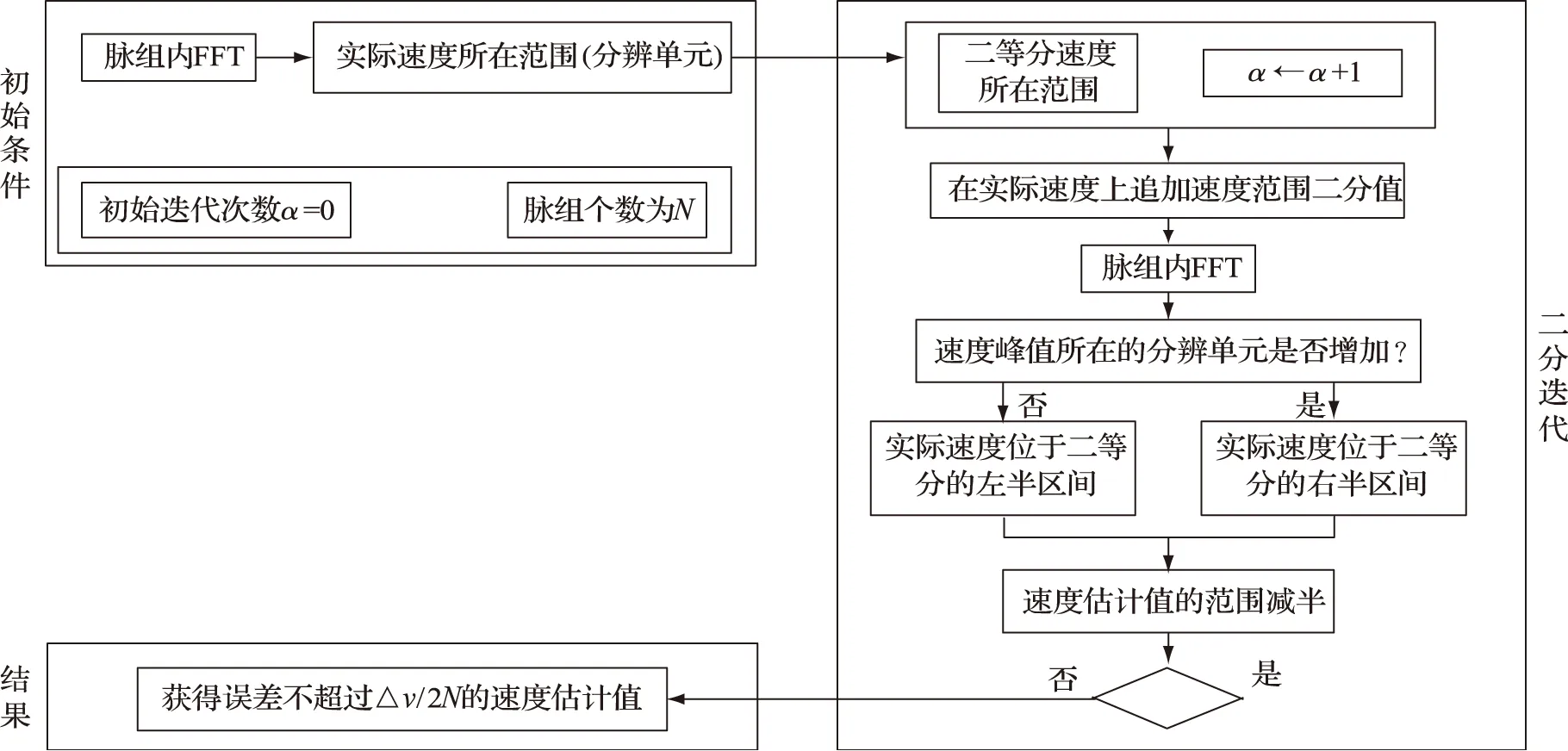
图2 DIM流程框图

设迭代次数为α，由于DIM采取的二分迭代处理，则相应的测速精度提高2α倍。从而，利用2α替代式(17)中的W，可得

2α≥N

(18)

式(18)即为利用DIM的迭代终止条件。

如上分析可知，DIM关键是通过二分迭代处理，寻找临界附加速度，使得峰值所在的速度分辨单元数恰好开始增加一个单元(小于该临界值不增加)。经过DIM处理后,速度误差为△v/(2N)。由此可知，经DIM处理后的测速误差较式(8)提高了N倍，从而由此导致的距离移动不超过半个距离单元。

由式(18)可得DIM处理所需的迭代次数为

2α≥N⟹α≥log2N

(19)

例如，假设脉组间步进频信号的脉组个数N为32时，由式(19)可知，DIM中只需5次迭代操作便可获得精度提高32倍的速度估计值。

DIM中每次二分迭代运算即为脉组内(对应M个离散值)的FFT处理，对应的计算复杂度为O(Mlog2M)。因此，结合式(19)可得DIM的计算复杂度为O(αMlog2M=Mlog2Mlog2N)。

4 计算机仿真试验

设雷达系统参数(可参考文献[6])为：第一脉组信号的中心频率f0= 1 GHz，脉组数N=32，脉组间频率增长步长△f=10 MHz，则fn=f0+(n-1)△f(n=1,2,…,N)，光速c=3×108m/s，则距离分辨率△R=c/(2N△f)≈0.47 m。脉组内相干脉冲数M=64，第一组脉冲串的脉冲重复频率fr=5000 Hz，则最大不模糊速度v0=fr×λ0/2=750 m/s。第n组脉冲串的PRI为Tnp=c/(2v0fn)，则Tns=MTnp。假设目标由3个分别位于150 km+20△R、150 km+22△R和150 km+24△R的散射体组成，且为匀速运动的刚体。设目标径向速度分别为5.8594 m/s(即△v/2，△v为速度分辨率)、60 m/s和400 m/s。利用在脉组内的FFT处理获得的速度测量值对距离-多普勒耦合进行补偿，补偿后的目标距离像如图3所示。

从图3可看出，尽管补偿了距离-多普勒耦合对距离像的影响，但由于利用FFT测量的速度值的量化误差依然影响目标距离像，量化误差大小决定距离像质量的好坏。比如当速度为5.8594 m/s即△v/2 (△v=11.7188 m/s)时，利用FFT测速时对应的测速误差恰为最大值△v/2，因此对距离像的影响最严重，如图3(a)所示。

(a) v=5.8594 m/s目标距离像

(b) v=60 m/s目标距离像

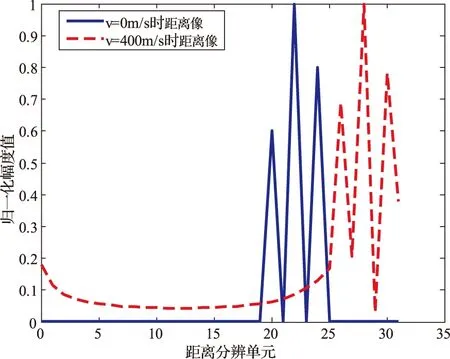
(c) v=400 m/s目标距离像

图3 利用FFT测速补偿距离-多普勒耦合后的距离像的比较

为了方便对比采用二分迭代法(DIM)前后目标测量速度值逼近实际速度值的程度，设目标相对径向速度分别为5.8594 m/s (即△v/2)、11.7188 m/s (即△v)、17.5782 m/s (即3△v/2)、60 m/s、100 m/s和400 m/s。测量速度值对比如表1所示。表中，CV表示速度估计值，AE表示估计速度的绝对误差。

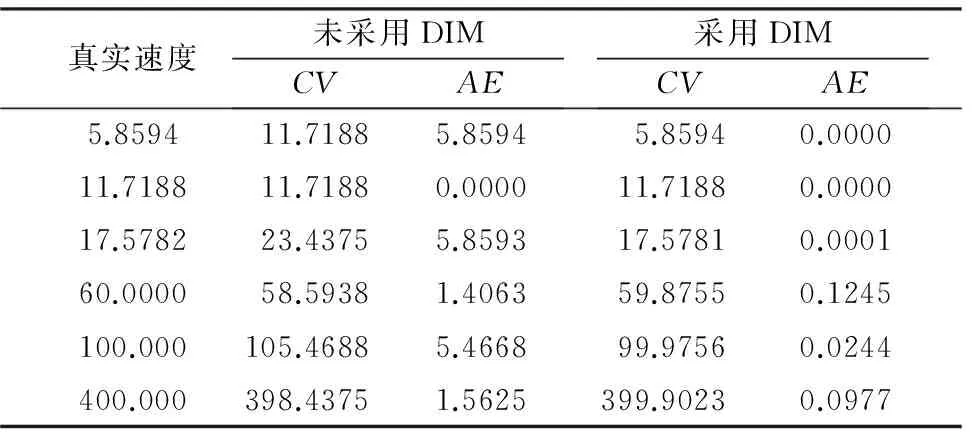
表1 采用二分迭代法(DIM)前后速度测量值(m/s)对比

从表1可知，当速度为5.8594 m/s时，通过FFT测速时具有最大测速误差△v/2，而当速度为11.7188 m/s时速度估计精度最高。然而，采用DIM后，对上述速度值均能获得高精度估计值。因此，该方法能有效提高目标速度估计精度。

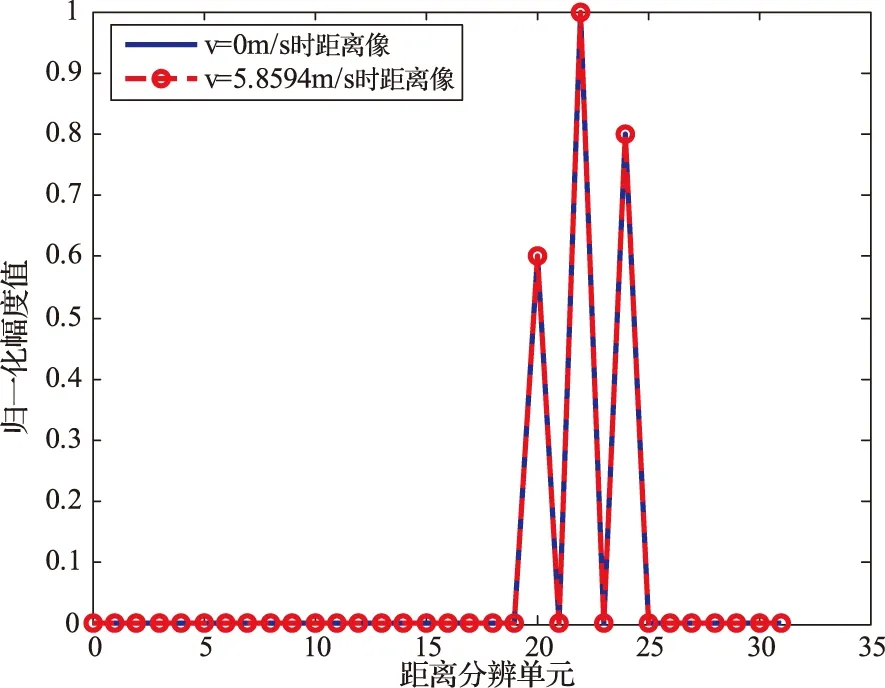
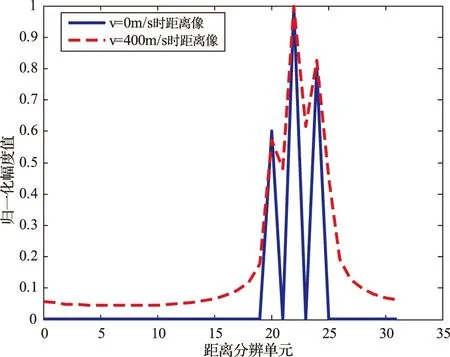
下面分析采用DIM后测速误差对合成距离像的影响。当目标速度分别为5.8594 m/s、60 m/s和400 m/s时，利用DIM处理后对应的速度估计值补偿距离-多普勒耦合，得到的目标合成距离像如图4所示。

(a) v=5.8594 m/s目标距离像

(b) v=60 m/s目标距离像

(c) v=400 m/s目标距离像

图4 速度变化时利用DIM测速后获得的距离像比较

从图4可知，当目标在不同的径向速度下，经过DIM处理后获得的距离像沿距离维的移动及扩展均可忽略，较好地反映了目标真实距离信息(速度为0时的距离像)。

通过比较图3和图4可知，采用DIM前由测速时对应的量化误差仍影响目标距离像的移动及扩展，但采用DIM后由于获得了较高精度的速度估计值(如表1)。因此，进行相关补偿后获得的目标距离像与目标真实距离像基本一致，从而验证了DIM能有效解决量化误差对距离像的影响。

5 结束语

针对在脉组间步进频信号的脉组内利用FFT测速时的测速误差(最大测速误差对应的目标距离像沿距离维走动高达round(N/2)个分辨单元)，提出了简称为DIM的二分迭代方法。该方法在脉组内脉冲个数(对应图1中M值)不变的情况下，通过log2N次迭代操作即可使测速精度提高N倍，通过相关补偿后距离像的移动不超过半个距离单元。由于该方法的测速精度提高速率是以2为底的指数增长，且每次迭代为脉组内FFT操作，因此DIM具有较少的计算量，便于工程实现。

[1] Taylor J D.Ultra-wideband radar technology[M]. New York: CRC Press, 2001.

[2] 毛二可, 龙腾, 韩月秋. 频率步进雷达数字信号处理[J]. 航空学报, 2001, 22(6): 16-25.

[3] 刘峥, 张守宏. 步进频率雷达目标的运动参数估计[J]. 电子学报, 2000, 28(3): 43-45.

[4] 王德纯. 频率步进雷达及其在小目标检测中的应用[J]. 现代雷达, 2006, 28(2): 1-4.

[5] 倪友平, 姜卫东, 陈曾平. 步进频信号散射中心的提取及目标识别[J]. 现代雷达, 2005, 27(9): 1-4.

[6] Shen Y Y, Liu Y T. A step pulse train design for high resolution range imaging with Doppler resolution processing [J]. Chinese Journal of Electronics, 1999, 8(2): 196-199.

[7] 彭卫,汪学刚,赵建宏，等.基于常规多普勒滤波器组结构的合成宽带距离像性能分析 [J]. 航空学报, 2009, 30(6): 1096-1102.

[8] Peng W, Wang X G, Zhao J H. Methods of eliminating Doppler dispersion in synthetic wideband signal//Proceedings of IEEE International Conference on Microwave and Millimeter Wave, Beijing, China, 2008: 1540-1543.

A method of improving estimated velocity error using stepped frequency pulse trains

YIN Hua-qiao1, WANG Shun-xi2

(1.No.38 Research Institute of CETC, Hefei 230088;2.Unit 61195 of the Chinese PLA, Nanjing 210008)

The Dimidiate Iterative Method (DIM) is proposed to remove the impacts made by the velocity error on the synthetic range profile when the Fast Fourier Transform (FFT) is used in a pulse train of the stepped frequency pulse trains (SFPTs) signal. The estimated velocity precision can be increased by N times via log2N iteration processing using the DIM, where N is the number of pulse trains. Moreover, the migration of the synthetic range profile does not exceed half a range resolution bin after the compensation. Besides, this method can save computation since the precision is grown exponentially with log base 2 and the FFT processing in pulse trains is carried out for each iteration. The effectiveness of the method is verified through the simulation.

stepped frequency; velocity error; synthetic range profile; Fast Fourier Transform

2014-04-15;

2014-05-20

尹华桥(1966-),男,高级工程师,研究方向:雷达系统;王顺喜(1978-)，男，工程师，硕士，研究方向：电磁场与微波技术。

TN957.51

A

1009-0401(2014)02-0033-05