公路隧道衬砌有限元分析

周宪伟,赵新江,李宏宇

(1.黑龙江工程学院 土木与建筑工程学院，黑龙江 哈尔滨 150050；2.龙口住总鸿运房地产开发有限公司，山东 烟台 265701；3.辽宁省建设科学研究院，辽宁 沈阳 110015)

公路隧道衬砌有限元分析

周宪伟1,赵新江2,李宏宇3

(1.黑龙江工程学院 土木与建筑工程学院，黑龙江 哈尔滨 150050；2.龙口住总鸿运房地产开发有限公司，山东 烟台 265701；3.辽宁省建设科学研究院，辽宁 沈阳 110015)

衬砌内力的计算是公路隧道设计的关键问题，计算结果的准确性会影响结构的安全性与经济性。文中采用有限元分析软件MIDAS用有限元法计算衬砌的内力和变形。衬砌结构采用梁单元，围岩抗力采用面弹簧单元模拟，墙脚支座用点弹簧单元模拟，计算荷载为竖直方向和水平方向围岩压力。通过分析得到衬砌最大位移的大小和位置，衬砌结构的内力分布及数值大小。另外，根据分析结果得到抗力最大值为侧墙距墙脚1/3处，图形呈镰刀形分布，与经验确定的抗力分布图形式一致，分析结果和手算结果规律一致。

衬砌；MIDAS；抗力；内力

公路隧道的衬砌结构形式常采用的是复合式衬砌和整体式衬砌，这两种形式的衬砌的断面一般为曲墙拱顶。在衬砌结构设计时，可采用荷载结构法，荷载—结构模型认为地层对结构的作用只是产生作用在地下建筑结构上的荷载(包括主动地层压力和被动地层抗力)，衬砌在荷载作用下产生内力和变形，与其相应的计算方法称为荷载结构法[1]。根据所得到的衬砌内力进行构件截面设计。在以往的设计中采用力法方程进行手算求解，对于抗力的考虑是根据经验假定弹性抗力为镰刀形分布，由3个特征点控制，抗力零点b，一般与对称中线夹角为φb，φb=40°～60°；抗力零点a在曲墙墙脚处(由于墙脚与围岩间摩擦力很大，故此处无水平位移，因而无弹性抗力)；最大抗力点h假设在衬砌跨度最大处，通常h点在抗力区2/3处。在计算过程中,变位置的计算采用辛普生法近似计算。手算法的计算过程复杂，工作量大，而且计算精确度不高，为了减少工作量，提高计算精度，本文采用有限元软件MIDAS对衬砌进行有限元法内力计算。

1 衬砌荷载计算

荷载计算采用《公路隧道设计规范》中推荐的方法进行计算，根据荷载等效高度hq划分超浅埋、浅埋和深埋段，然后根据相应公式计算垂直压力和水平压力，两种压力均近似按照均布荷载考虑。本文选取浅埋段进行研究，围岩等级为Ⅳ级[2]。

垂直土压力[3]

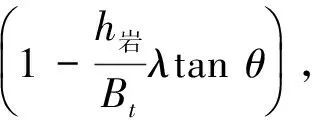
φ=30°，θ=0.8φ=0.8×30°=24°，φc=50°.

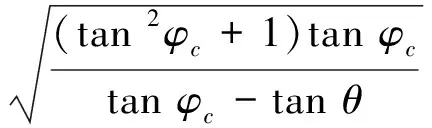
0.16。

式中：φc为围岩计算内摩擦角，θ为滑裂面摩擦角，β为滑裂面与水平面夹角，λ为侧压力系数。

q=315.4 kPa.

水平土压力

e=(e1+e2)/2=(γHλ+γhλ)/2=70.504 kPa.

由于二次衬砌承受的荷载占外荷载的40%，所以二次衬砌承受的垂直荷载和水平荷载分别为

q′=0.4q=126.151 8 kPa，

e′=0.4e=28.201 5 kPa.

2 衬砌有限元模型建立

本次研究的衬砌为复合式衬砌，横断面为曲墙拱顶，衬砌厚度为0.35 m，纵向单位长度1.0 m[4]。衬砌单元采用梁单元，单元长度为1 m。周围岩土体对衬砌结构的抗力采用与衬砌梁单元弹性连接的面弹簧模拟，面弹簧的弹性系数根据围岩等级确定。本文选取截面处围岩等级为Ⅳ级，抗力系数取k=0.5×106kN/m3。面弹簧的单元宽度为1 m，单元长度取1 m，地基反力系数为0.5×106kN/m3，弹簧单元只受压不受拉。衬砌有限元模型如图1所示。

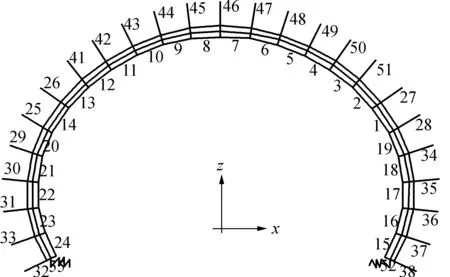
图1 衬砌有限元模型

3 荷载及约束条件的施加

本文衬砌采用C30混凝土，泊松比取0.18，容重取25 kN/m3。垂直荷载施加在拱顶，水平荷载施加在拱顶和侧墙，均以均布荷载施加在每个单元上，如图2所示。

曲墙墙脚处由于墙脚与围岩间摩擦力很大，故此处无水平位移，克服围岩抗力有转角。所以在墙脚处设置点弹簧支座，水平方向限定位移，竖直方向位移为0，转角刚度KRy=1 786.46 kN·m/rad。

模拟围岩抗力的面弹簧端点处水平位移，竖直位移和转角均为0[5]。

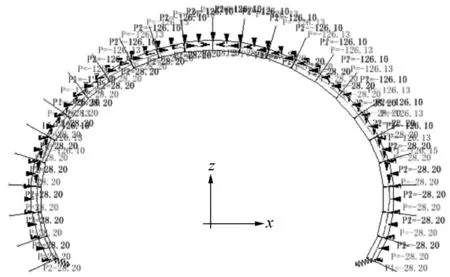
图2 荷载及约束的施加

4 有限元分析[6-7]

对衬砌结构进行静态非线性分析。得到衬砌的位移图、轴力图、剪力图、弯矩图和围岩对衬砌产生的抗力图。

4.1 衬砌位移

衬砌总位移如图3所示，衬砌左半部分各单元位移具体数值如表1所示。

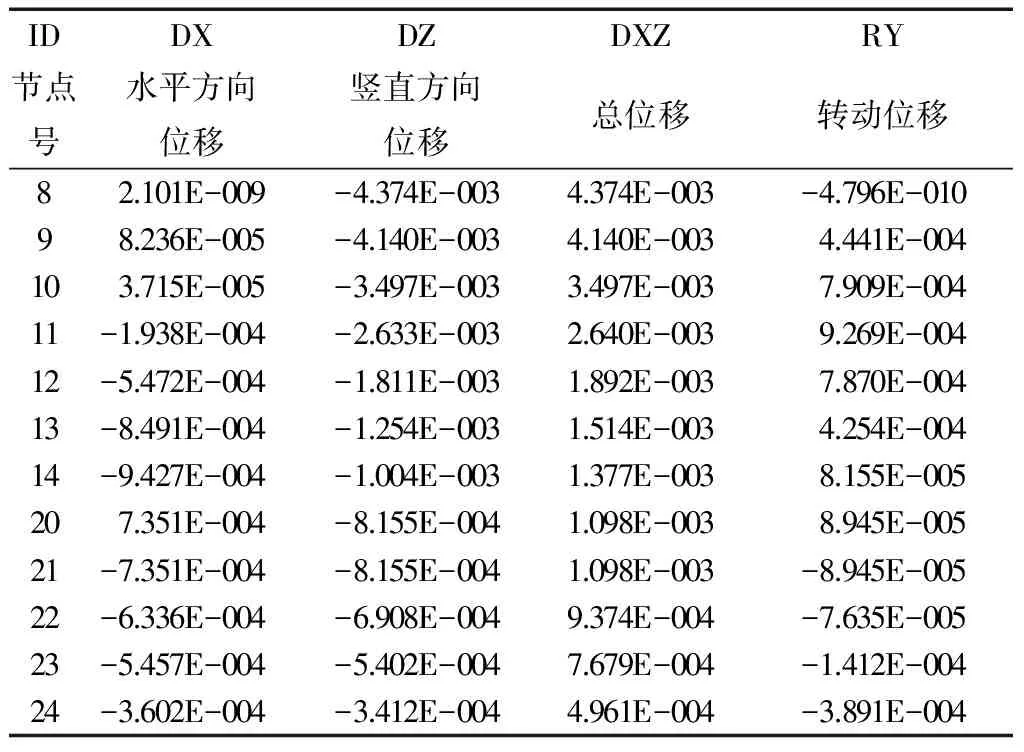
表1 衬砌各单元位移 m

图3 衬砌总位移图

由分析结果可知，竖直位移和总位移最大处为拱顶，均为4.4 mm，水平位移最大处为第2单元和14单元，位移值为0.9 mm。

4.2 围岩抗力

本文采用面弹簧来模拟围岩对衬砌产生的抗力，分析结果中面弹簧的轴力即围岩抗力。面弹簧的抗力图如图4所示，各弹簧单元的轴力数值如表2所示[7]。

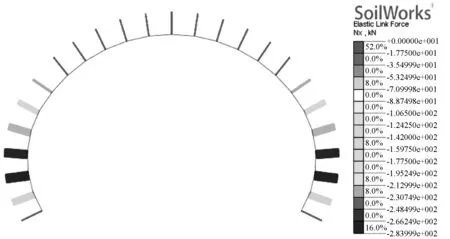
图4 抗力图

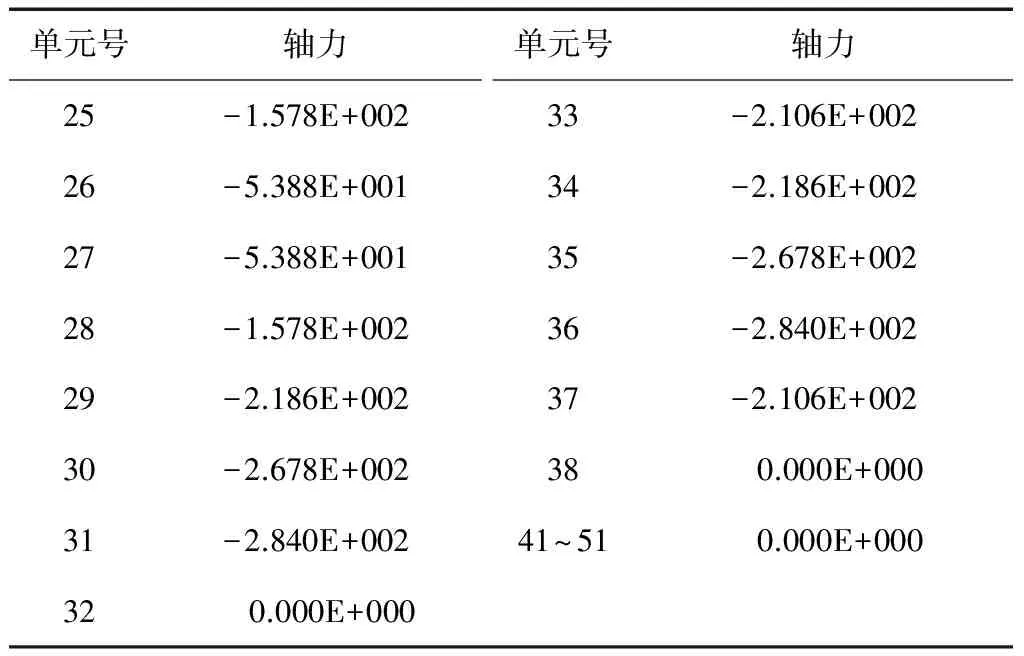
表2 弹簧单元轴力值 kN

由分析结果可知，连接弹簧轴力最大值发生在31单元和36单元，轴力值为284 kN，轴力零点为墙脚处及51单元和41单元处。根据连接弹簧的轴力值绘出衬砌抗力分布图如图5所示，图形呈镰刀形分布，与经验确定的抗力分布图形式一致。

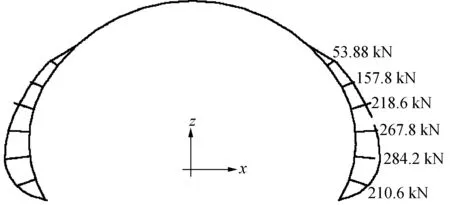
图5 衬砌抗力分布图

4.3 衬砌内力

衬砌内力包括轴力、剪力和弯矩，衬砌左半部分各单元的内力见表3，内力图如图6所示。

表3 衬砌内力

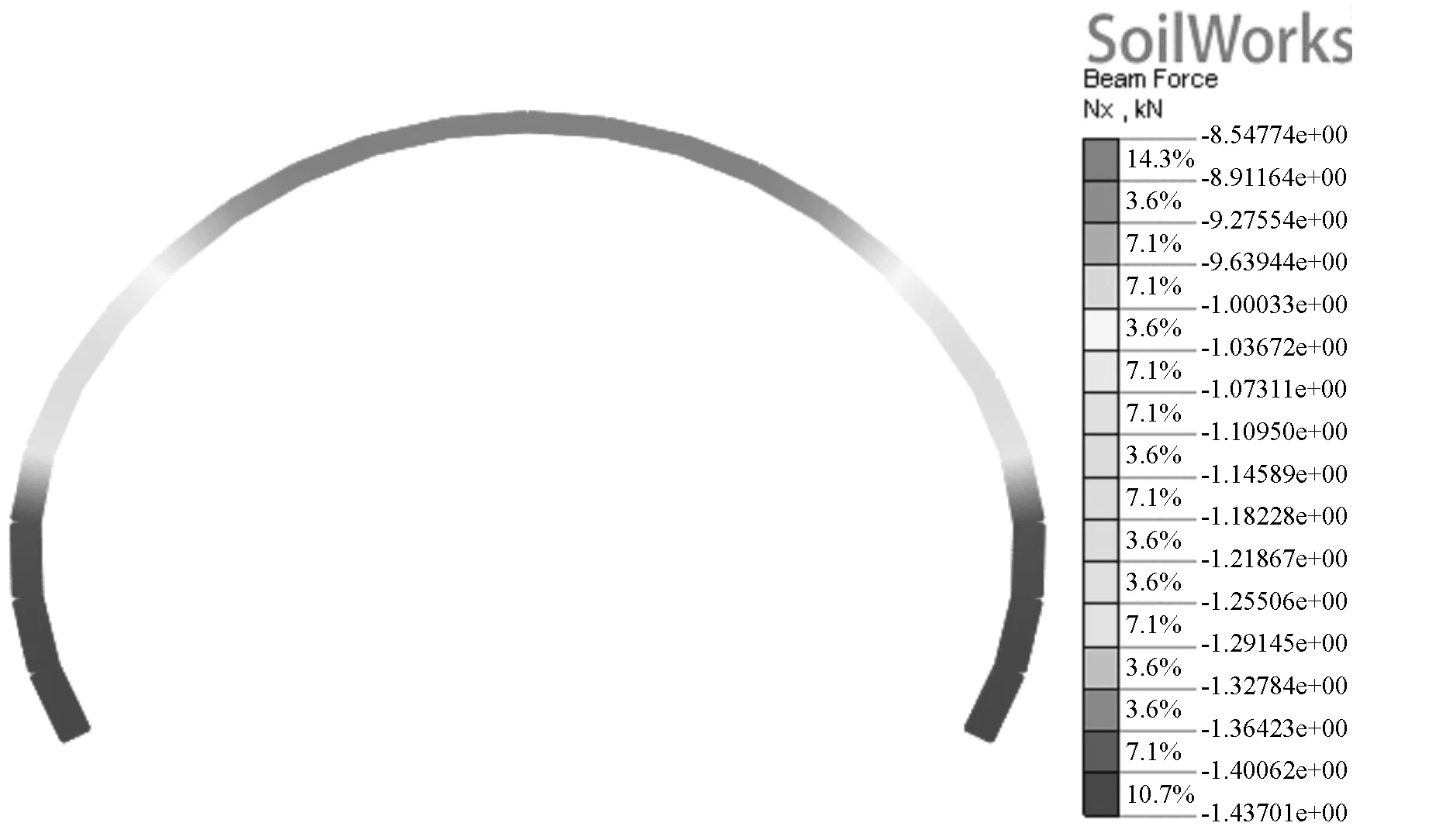
(a)轴力图

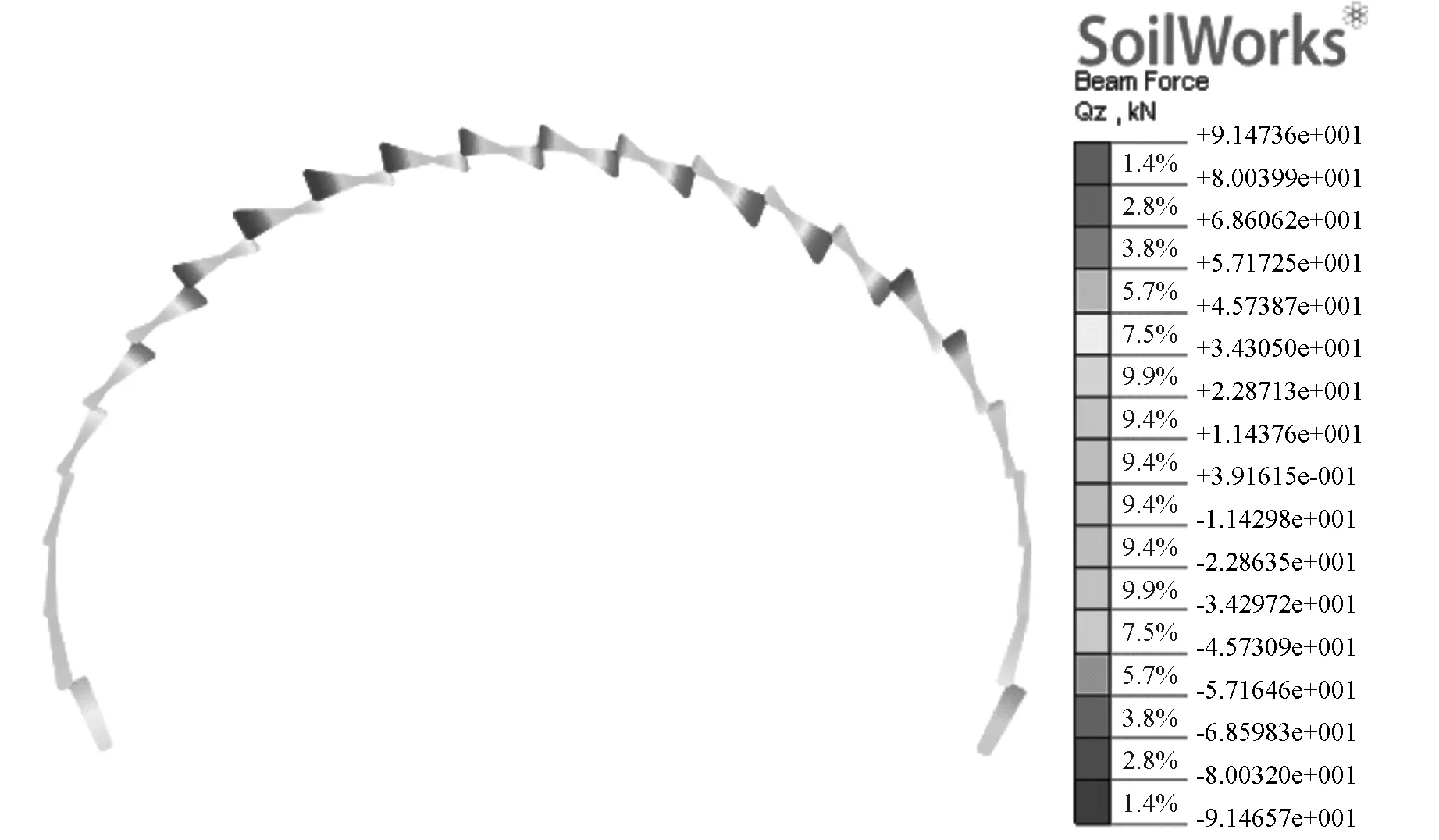
(b)剪力图

(c)弯矩图

由分析结果可知，轴力最大值为1437 kN，在墙脚处；剪力最大值为91.47 kN，在拱顶两侧；正弯矩最大值为48.96 kN·m，在12单元，负弯矩最大值为-29.48 kN·m,在拱顶处。

手算法主要采用结构力学中超静定结构的力法来求解，对于力法方程中的系数采用辛普生法进行计算，得到的衬砌轴力图和弯矩图如图7所示[8]。

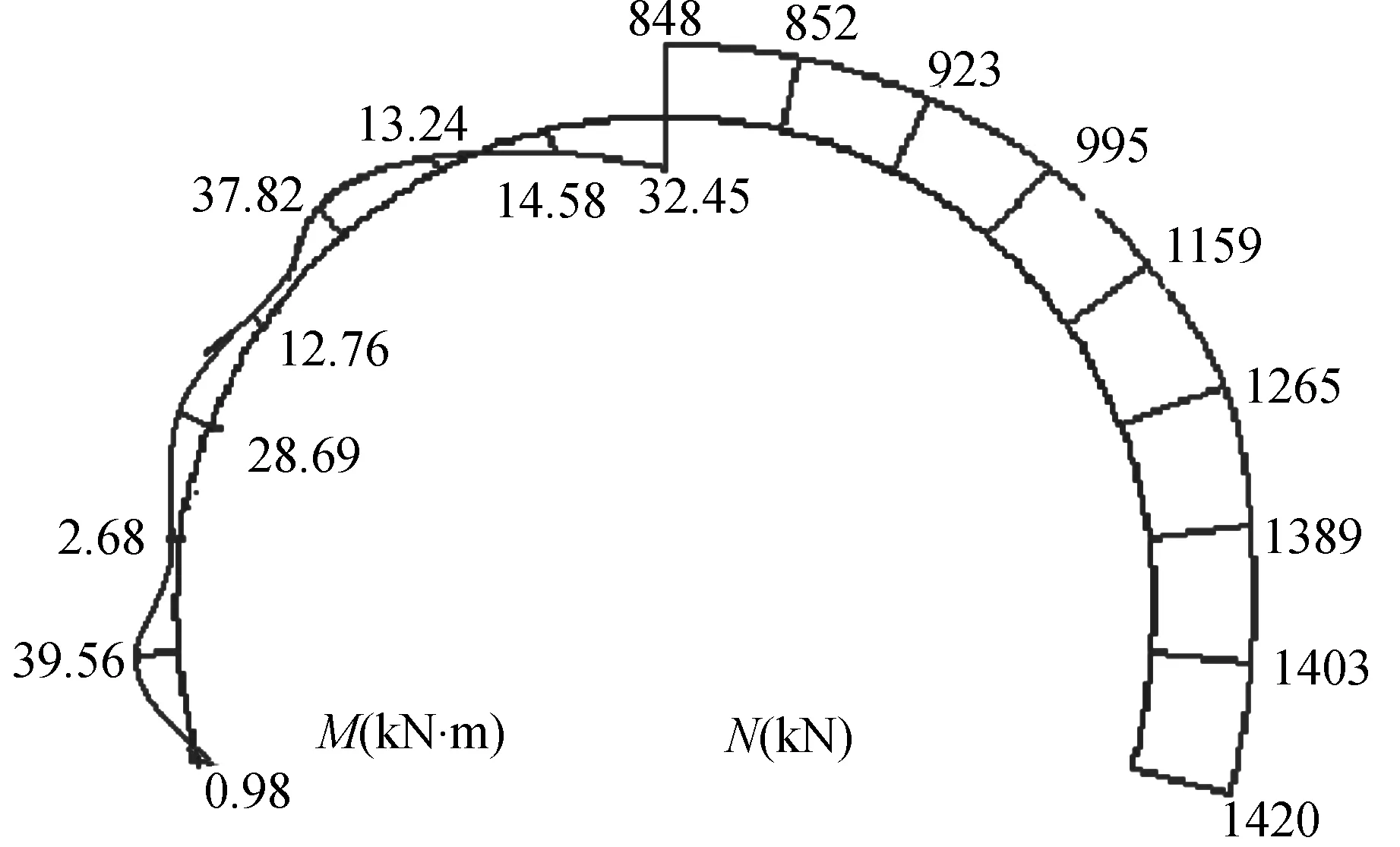
图7 手算法得到的衬砌轴力图和弯矩图

通过模拟结果和手算内力的比较，弯矩和轴力分布形式一致，但数值略有差异。模拟结果较手算结果轴力和弯矩偏大，其原因主要是手算法抗力分布和数值为经验法确定，这与实际不完全相符所导致的[9]。有限元分析方法较手算结果更加接近实际，且计算速度快，计算精度高，节省时间[10]。

5 结 论

有限元法计算衬砌的内力时衬砌结构采用梁单元，围岩抗力采用面弹簧单元模拟，墙脚支座用点弹簧单元模拟，计算荷载为竖直方向和水平方向围岩压力。分析结果显示：竖直位移和总位移最大处为拱顶，最大总位移值为4.4 mm，水平位移最大处为拱顶与侧墙交点附近，最大值为0.9 mm；抗力最大值为侧墙距墙脚1/3处，图形呈镰刀形分布，与经验确定的抗力分布图形式一致，轴力最大值在墙脚处，剪力最大值在拱顶两侧，衬砌内侧受拉的最大弯矩发生在拱顶处，衬砌外侧受拉的最大弯矩发生在拱顶和侧墙顶中点附近。分析结果和手算结果规律一致，但较手算结果更加接近实际，且计算速度快，节省时间。

[1]胡兴国.结构力学[M].4版.武汉：武汉理工大学出版社，2012.

[2]覃仁辉.隧道工程[M]. 重庆：重庆大学出版社，2011.

[3]徐学燕.高等土力学[M].哈尔滨:哈尔滨工业大学出版社，2008：17-56.

[4]重庆交通科研设计院.JTG D70-2004 公路隧道设计规范[S].北京：人民交通出版社，2004.

[5]张成红. 隧道衬砌结构内力有限元分析[J].中国高新技术企业，2011，3(5)：1-3.

[6]赵尚毅.地下隧道衬砌结构内力计算方法探讨[J].后勤工程学院学报，2007，23(4)：31-32.

[7]韩向阳.隧道衬砌结构截面内力的影响因素分析[J].岩土工程界，2008，6(5)：30-32.

[8]徐秉业，刘信声.应用弹塑性力学[M].北京：清华大学出版社，2007：73-126.

[9]路美丽.铁路隧道衬砌结构内力的影响因素分析[J].铁道建筑技术，2008(S2)：189-193.

[10]张文正.基于实测数据的隧道衬砌受力分析[J].地下空间与工程学报，2009(2): 1-3.

[责任编辑：刘文霞]

Analysis of highway tunnel lining with finite element method

ZHOU Xian-wei1,ZHAO Xin-jiang2,LI Hong-yu3

(1.Heilongjiang Institute of Technology,Harbin 150050，China;2.Longkou Zhuzong Bonanza Real Estate Development Co.,Ltd.,Yantai 265701,China;3.Construction Science Research Institute of Liaoning Province,Shenyang 110015,China)

Calculation of internal force of lining is the key problem in the design of highway tunnel. The accuracy of the calculation results will affect the safety and economy of the structure. A finite element software MIDAS is used to analyze the internal force and deformation of lining. The lining structure consists of beam elements,the surface resistance of rock spring element to simulate,a support spring element to simulate,load calculation for the horizontal and vertical surrounding rock pressure. Through analysis the location and data of the maximum displacement are obtained as well as the distribution and values of internal force. The maximum resistance is at the side wall of distance foundation 1/3. Graphics is sickle shaped in the distribution map form,which is consistent with empirically determined. The results of the analysis and calculation results are consistent.

lining;MIDAS;resistance;internal force

2013-10-17

周宪伟(1977-)，男，讲师，研究方向:岩土与地下工程.

U455

A

1671-4679(2014)05-0020-04